基于直观想象核心素养的数学教学实践探究
2022-04-20陈丽美
文/陈丽美
引 言
培养学生的核心素养是“立德树人”的具体体现。其中,直观想象素养在高中数学学科核心素养中占有重要地位。高中数学教师基于直观想象素养开展教学活动,不但有助于学生掌握解题的有效思路,而且对学生核心素养的提升具有重要促进作用。
一、构建数形联系
提高学生的数形结合意识,增强运用数形结合思想解答数学问题的能力,有助于提升学生的直观想象素养。在教学过程中,教师应注重为学生讲解构建数形联系的具体思路,如从形到数,可通过构建平面或空间直角坐标系实现;而从数到形,则可根据所学知识绘制对应的函数图像、平面及立体几何图形。为使学生认识到构建数形结合联系的重要价值,教师可结合学生所学为其讲解相关的例题,促使学生养成应用数形结合解题的良好习惯。另外,为促使学生将所学的理论转化为能力,教师应做好训练习题的设计,组织学生开展专题训练活动,提高学生构建数形联系的熟练程度,积累相关的经验与技巧。如通过以下习题的训练,教师可使学生认识到构建平面直角坐标系时应注重运用题干中的直角关系,以减少在解题中的运算量[1]。
已知ABCD为梯形,其中∠BAD =∠ABC =90°,AB = BC =AD,点E为CD的中点,AE和BD交于点F,设则x-y = ____。
学生可以将题干中描述的图形放到平面直角坐标系中,将点转化为具体坐标,实现“形”向“数”的转化,如此便可将线段之间的关系直观地呈现出来,而后通过点的运算及平面向量知识,解出x、y的具体值。需要注意的是,学生应充分运用图形中的直角关系构建坐标系,以降低计算复杂度,提高计算效率。
二、借助几何直观理解问题
几何图形本身具有直观性特点。学生通过对数学问题的认真思考、合理想象画出相关的图形,借助几何图形更容易理解问题、解决问题。为提高学生利用几何图形理解、解决问题的能力,教师应注重引导学生做好常见几何图形的汇总。这里的几何图形既包括从课本中学到的几何图形,也包括在生活中看到、积累的几何图形。教师可以要求学生认真分析一些几何图形的特点,在头脑中存储清晰的模型,为更好地解决数学问题提供依据。另外,为使学生学会运用几何直观理解、解决问题,教师应注重结合学生所学的数学知识创设相关的问题情境,并通过多媒体技术为学生进行动态的展示,在增加数学课堂趣味性的同时,使学生更好地掌握分析数学问题的技巧,迅速解出正确答案。例如,教师在课堂上可用多媒体技术为学生讲解如下习题的解答过程。
已知长方体ABCD-A1B1C1D1中AB、BC、BB1的长分别为6、5、4,则从点A沿表面到点C1的最短距离为________。
求解几何体表面上两点间的最短距离一般采用展开方法,借助几何直观进行分析。因沿着不同的棱剪开计算的结果不同,因此,教师可用多媒体课件为学生展示如下可能的情境。
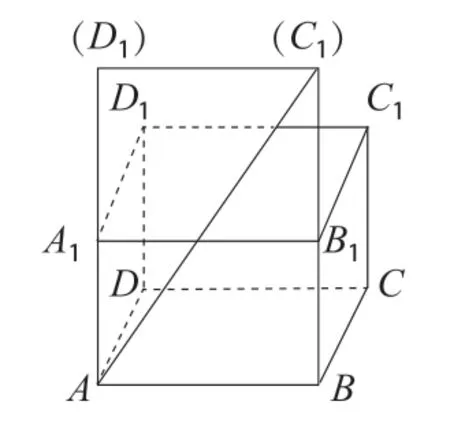
图1

图2

图3

该题具有一定代表性,如果对题意理解不清晰,那么很容易漏掉相关情境,导致出错。教师借助多媒体技术为学生直观展示沿不同棱展开不同平面时AC1的具体情形,更容易深化学生的认识,降低学生的理解难度,启发学生在以后的学习中注重几何图形的应用,找到解决立体几何问题的正确思路[2]。
三、借助图形描述问题
借助几何图形描述问题属于直观想象的范畴。事实上,运用图形描述问题,化抽象为具体,更容易把握问题的本质。为使学生学会使用图形描述问题,为解决问题做好铺垫,教师应要求学生脚踏实地,牢固掌握基础知识。高中数学中与图形相关的知识点有各类函数的图像、圆锥曲线、向量的几何意义、复数的几何意义等。教师可以要求学生根据题干描述,充分挖掘隐含在题干中的相关图形,通过运用转化思想,运用图形准确描述问题。同时,为使学生认识到运用图形描述问题的重要价值并灵活应用于解题中,教师应注重为学生进行习题讲解。
例题:已知复数z = x + yi(x, y∈R),满足|z|≤1,则y≥x -1的概率为________。

图4
借助图形描述问题是直观想象素养中非常重要的方面。该题基于对复数知识的理解,运用复数的几何性质将已知条件转化为对应的图形,将要求解的问题转化为图形中面积之间的问题,化抽象为直观,能优化解题思路,使学生认识到运用图形描述问题的意义所在,养成运用图形描述问题的良好习惯。
四、通过空间想象认识事物
直观想象素养强调空间想象的重要性。在高中数学教学中,为更好地提升学生的空间想象能力,教师应鼓励学生联系生活中的事物,抽象出相关事物的轮廓,必要情况下可组织学生开展相关的实践活动,要求学生使用剪刀、纸片等拼接相关的立体几何图形。同时,教师要注重从不同角度为学生展示常见立体几何图形的模型,给其留下更为深刻的印象。另外,为帮助学生构建平面与立体几何图形之间的关系,深化对立体几何图形的认识,教师应结合学生所学的知识,在课堂上设计相关问题,要求学生通过空间想象进行解答。例如,教师可要求学生解答如下习题。
如图5所示,三棱柱ABC-A1B1C1底面为等边三角形,侧棱AA′和底面ABC垂直,AB=9,AA′=3,在四边形ABB′A′内存在一点P,其到AA′、A′B′的距离均为1。若D为BC上靠近C的四等分点,过点P且与A′D平行的直线交三棱柱于P、Q两点,则点Q所在的平面为______。

图5
教师可以要求学生根据给出的图形,逐一想象点P的位置。学生结合自身经验,经过想象可得点Q所在的平面为平面ABC。为验证学生想象的结果,教师可在课堂上运用多媒体技术为学生动态展示,结果表明学生的想象是正确的,如此能提高学生的解题自信心。
通过空间想象认识事物是锻炼学生直观想象核心素养的重要方法。该题以立体几何中的动点为背景设问,考查学生对立体几何各要素空间关系的认识及熟练程度。分析该习题能很好地锻炼学生的空间想象能力,加深学生对立体几何图形的认识[3]。
五、借助训练积累想象经验
教学实践中,教师应注重给学生提供训练机会,使其积累运用直观想象解决数学问题的经验,一来更好地巩固所学,二来使其认识到直观想象在解答数学习题中的重要作用。为获得预期的训练效果,教师应认真分析学生已经具备的知识,做好训练习题的优选,拓展学生的视野,让学生掌握运用相关图形、相关模型解题的技巧。
例题:已知圆(x-1)2+ (y-2)2= 1上存在一动点P,O为坐标原点,向量在向量=(2,1)方向上投影的最大值为_____。


图6
解决数学问题的思路多种多样,为了有针对性地提升学生的直观想象素养,教师应结合自身教学经验,认真设计习题,促使学生运用相关图形理解与解决数学问题,使其在更好地把握数学知识本质的同时,提高解题的灵活性。
六、借助总结提升想象能力
为更好地培养学生的直观想象素养,教师应引导学生充分认识到总结的重要性。教师既要注重在课堂上合理安排教学容量,给学生留下课堂总结时间,尽量使其当堂消化、吸收所学,又要引导学生养成善于总结的良好习惯。
例题:将一个正四面体截取四个顶点,形成如图7所示的八面体,其中四个面为正六边形,四个面为正三角形。若此八面体所有棱长均为1,则其体积为________。
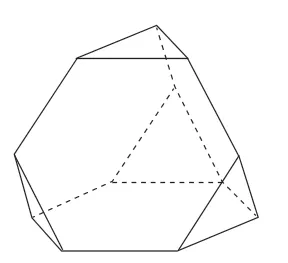
图7
根据经验,学生在解题时可将该八面体补成一个正四面体,其边长之间的关系便一目了然,然后使用正四面体的体积减掉减去的体积,便可求出最终结果。
结 语
培养学生的直观想象素养需要长期坚持,尤其应将培养工作贯穿至整个高中阶段。为获得良好的培养效果,教师既要制订明确的培养目标,又要对教学内容进行合理的设计,注重直观想象素养的融入。另外,教师也应做好培养效果的评估,总结与反思培养过程中遇到的问题,不断提升学生的数学直观想象素养水平。
