一种新型运算放大器的设计与仿真

2022-04-20林宇刘洁陈思琪任烨磊章惠

科教创新与实践 2022年5期

林宇　刘洁　陈思琪　任烨磊　章惠

摘要：本文主要研究两级放大器，因补偿方式不同，而导致的增益，相位裕度，带宽等参数变化，造成的稳定性的变化。通过既定的设计电路指标，计算出电路所需结构的理论参数，并用cadence仿真带cascode补偿的两级运算放大器。通过设置变量，并用ADE中的扫描功能，观察变量的不同参数值对该电路的稳定性相关参数的影响变化趋势。经过分析，可以得出带密勒补偿的两级运算放大器可以显著补偿零极点，带调零电阻的两级运算放大器可以抵消密勒电容，cascode补偿结构的增益很小，但是会对补偿PSRR。同时，密勒补偿的电容值以及零点补偿的补偿电阻值的选择，至关重要，影响补偿“度”对带宽有很大影响。

关键词：电路;运算放大器;稳定性;补偿

自运算放大器诞生以来，基于运算放大器的电路设计以及相关的制造工艺，都已取得了重大进展。运算放大器的经常会探究速度、功耗、增益、摆幅、噪声等参数，但在实际设计中，这些参数相互牵制。设计过程中，明确最需要以及可以妥协的参数，对参数进行折中选择也需要对这些参数进行分析，这些量的探讨就是我们对运算放大器进行的稳定性分析。因此，本文主要对带cascode（NMOS管和PMOS管级联得来的结构）补偿的两级运算放大器进行研究与分析。

1、cascode补偿结构

我们常用的经过密勒补偿的两级运算放大器，会引入右半平面零点，从而使运放的频率响应的稳定性变差，除了加入调零电阻，我们也常用cascode compensation，即cascode补偿的方法来调节稳定性。

当Cc位于X点，为密勒补偿电路，当位于Y点，为cascode补偿电路，该电路是通过cascode将由X点经由电容Cc到输出的前馈通路截断。

2、设计图

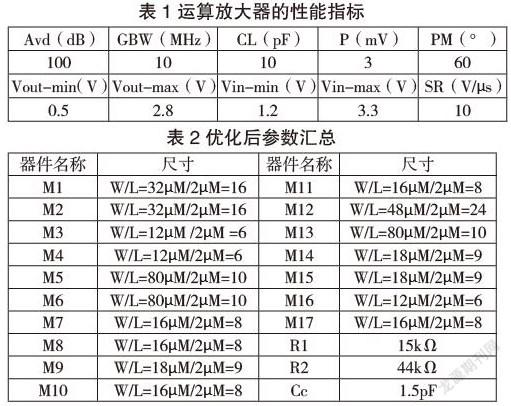
设计参数同表1，优化后参数同表2，但该结构改善了M12管，使其工作在了饱和区，处在稳定工作状态。

由于工艺库以及实际的误差等方面也会影响参数的大小，故我们需要在cadence中进行微调，来确保可以达到既定的设计指标。

3、电路仿真与优化

算放大器是由两级或多级放大器构成的高增益放大器，每级放大器至少包含一个极点，而每一个极点产生的最大相移为90°。因此，两级或多级放大器环路增益的总相移至少有两个极点影响，而其在高频时很可能达到或超过180°，此时如果环路增益的振幅大于0dB，則相位裕度变为零，即在低频时的负反馈在高频时变为正反馈，闭环系统不能稳定工作。因此，必须对环路增益加以修正，即进行相位补偿，使得环路增益具有足够的相位裕度，以保证闭环系统能够稳定工作。运算放大器常用两种相位补偿方法——极点分离法和零点补偿法。

（1）不同结构增益的对比

（2）带cascode补偿的两级运算放大器改变电容对相位裕度的影响

带cascode补偿的两级运算放大器改变电容对相位裕度的影响趋势和折叠式两级运算放大器的趋势无差异，但可由参数对比知cascode补偿的结构显著的降低了相位裕度。

（3）电路对比

若看Cc=3pF时的参数对比，可得出，零点补偿过后的二级运放电路的GBW最大，折叠式的最小。可知运算放大器的性能指标之间相互制约，折叠式的高增益是以牺牲GBW为代价得来的。同时由图也可知，补偿电阻值的选择至关重要，零极点补偿需精神选择参数。

4、结论

cascode补偿两级运算放大器该电路的优点是，可以将密勒补偿电容的前馈通路截断，使PSRR得到改善。与密勒结构相比，其主极点的位置一样，但cascode的非主极点较密勒补偿的非主极点频率更高，故cascode可以用相对较小的补偿电容来达到同样的频率补偿结果。

但是该电路的缺点是，原来的次主极点变为了一对共轭极点，而该极点的作用会导致gain-peaking，同时由于电容的作用，第二级放大管处于线性区，性能不稳定，以至于其放大的增益很低。

参考文献：

[1]魏廷存，陈莹梅，胡正飞.模拟CMOS集成电路设计[M].北京：清华大学出版社，2010：116-122.

[2]何红松.CMOS高性能运算放大器研究与设计[D].上海.复旦大学，2009：6-8.

[3]廖鹏飞.容性负载运算放大器的频率补偿技术研究[D].成都，电子科技大学，2014：14-16.