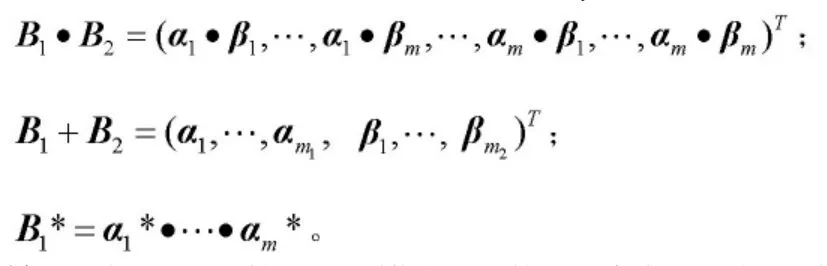保熵约简在模糊推理中的应用研究

华丹阳

（皖西学院 电子与信息工程学院，安徽 六安 230036）

1 研究现状

现代社会，伴随着信息技术日新月异的发展，人民群众的物质文化水平得到了极大的提升，用户对于产品的需求越来越趋向于“个性化”和“模糊化”。产品设计师面对的客户需求不再是0.618这样确定的数值，而是“价格便宜一些”“收货快一点”或者“好评多的”这些模糊的需求。为了解决这一实际问题，模糊理论应运而生，并伴随着新一轮的人工智能研究热潮，逐渐成为国内外科研工作者的研究热点［1-10］。

当前的功能求解模型往往以“与”“或”“非”命题逻辑为基础展开研究，这样固然可以将研究问题简化而易于处理，但是非0即1的僵化处理方式，无法体现用户的真实需求。基于此，本人及所在团队进行了一系列相关的研究工作，通过系统的模糊推理，提出了模糊功能树理论，用带模糊节点的树型结构进行模糊推理，并获得了一定的突破［11-12］。

然而，现有的功能树约简算法，往往侧重于对于重复部分的消除，这就导致了现有的约简算法只有在原有算法存在严重冗余的情况才有效，而对于一般的应用场景效果不明显。另外，现有算法集中于命题逻辑上的消减，这可能会造成在约简过程中消除一部分矛盾原子公式。而在模糊推理领域，矛盾原子公式的数量代表了推理创新性的程度，矛盾原子公式的减少，将造成推理创新性的损失，即“过度约简”。为了解决这一技术瓶颈，本文在不消减矛盾原子公式（即保持求解方案创新性不损失）的前提下，提出了模糊功能树约简理论，完善了模糊功能树的理论建设。

2 研究内容

2.1 与或非功能树的构建

在进行概念设计过程中，通常由用户需求出发，遵循自顶向下逐步求精的原则，把整体目标层层分解为子功能，通过实现每一个子功能，最终实现总的设计目标。在整个设计阶段，首要任务是找出一个适当的功能模型对设计过程进行描述。

鉴于此，本文首先把设计总目标设置成root节点，再由root节点出发，由上至下逐层分解，每一个leaf节点都是其上一层节点的延展，算法直到无法向下延展为止。通过将设计目标分解，可以构建出一棵与或非功能树，其构建过程体现了命题逻辑的主旨。其中，leaf节点定义为基本功能节点，非leaf节点定义为延展功能节点，“与”运算定义为合取“>”，“或”运算定义为析取“>”，“非”运算定义为否“'”，具体步骤如下：

1.令G1为与或非功能树中的一个节点，该节点对应的下一层节点为G2和G3，如果G2和G3之间的关系为“或”，则G1=G2>G3，代表的含义是：当G2或G3成立时，我们可以得到G1成立。

2.令G1为与或非功能树中的一个节点，该节点对应的下一层节点为G2和G3，如果G2和G3之间的关系为“与”，则代表的含义是：当G2成立并且G3成立时，我们可以得到G1成立。

3.令G1和G2为与或非功能树中的两个节点，如果G1和G2之间的关系为“非”，则G1=G2'，代表的含义是：当G2不成立时，我们可以得到G1成立。

4.两个或以上“或”关系用符号“Σ”代表；两个或以上“与”关系用符号“∏”代表；在通过专家系统搭建的与或非功能树中，节点的状态只有0和1这两种情况，其中0表示完全没有实现设计目标，1则表示完全实现设计目标。因此与或非功能树实际上可以转化为布尔运算。同时，由领域知识所建立的基本功能树，其基本功能只有非0即1两种状态：0代表没有实现相应的功能，1代表实现功能。这样功能树可以看成命题逻辑中的布尔代数运算：在功能树分解过程中，对应于“与”关系（“>”）可以使用与门（“”）表示；“或”关系（“>”）可以使用或门（“”）表示；“否”关系（“'”）可以使用非门（“”）表示。实例说明如下：

1.假设N1为与或非功能树的可延展节点，令其子节点是N2和N3，N2和N3的关系是“与”关系，则N1=N2>N3，公式代表的含义为：如果N2成立并且N3成立，那么N1成立（见图1）。

图1 “与”门

2.假设N1为与或非功能树的可延展节点，令其子节点是N2和N3，N2和N3的关系是“或”关系，则N1=N2>N3，公式代表的含义为：如果N2成立或N3成立，那么N1成立（见图2）。

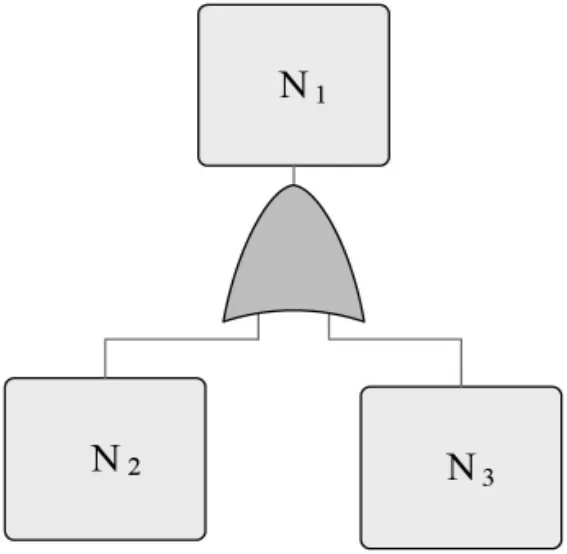
图2 “或”门

3.假设N1为与或非功能树的可延展节点，令其子节点是N2，N1和N2的关系是“非”关系，则N1=N2'，公式代表的含义为：如果N2不成立，那么N1成立（见图3）。

图3 “非”门

4.假设N1为与或非功能树的可延展节点，令其子节点是N2和N3，N2和N3的关系是“与非”关系，则N1=（N2>N3）'，公式代表的含义为：如果N2不成立或N3不成立，那么N1成立（见图4）。

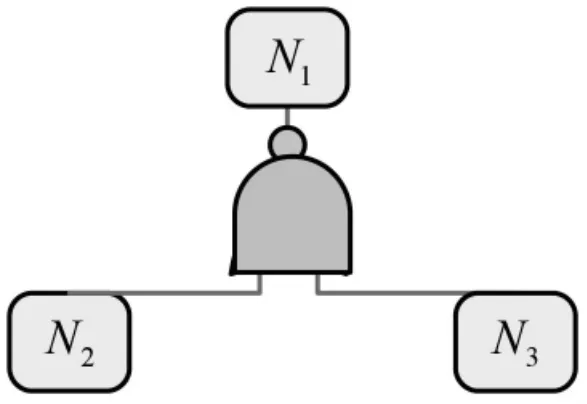
图4 “与非”门

5.假设N1为与或非功能树的可延展节点，令其子节点是N2和N3，N2和N3的关系是“或非”关系，则N1=（N2>N3）'，公式代表的含义为：如果N2不成立并且N3不成立，那么N1成立（见图5）。

图5 “或非”门

2.2 与或非功能树的模糊化

通过构建与或非功能树将设计目标形式化表示出来的方法，在认识科学中属于一种典型的确定性推理方法，即对于集合中的任何一个特点对象，其确定隶属于其中的一个集合。对于非0即1的二进制计算机科学来说，这种方法一直以来被广泛接受。

然而，在日常生活中，对象、集合、关系之间并没有如此明确的划分。例如“高山”：对于一个对象“山”，究竟海拔多少以上，可以归为“高山”这个集合；“大河”：对于一个对象“河”，究竟流域多少以上，可以归为“大河”这个集合。这些集合并没有明确的标准，原因在于现实世界中大部分对象与集合都是不精确的。在当今人工智能的研究领域，不确定性推理反而是国内外学者重点突破的方向。模糊集理论系统地阐述了对象与集合的模糊关系，在模糊集理论中，对象不再是完全隶属于或完全不隶属于某个特定集合，而是通过隶属函数描述这两者之间的隶属关系。通过研究，本文将模糊理论应用于与或非功能树模型中，赋予与或非功能树中每个叶子以特定的模糊值，完成由与或非功能树到模糊功能树的转换过程，这一转换过程可以通过数学推导展示。

本文用公式pi和公式Gj分别代表树形结构当中的中间节点与最底层叶子节点，当叶子节点相同时，相对应的公式也相同。对于结构中的一个节点，假如该节点的功能可以实现，那么令Gj=1（或pi=1）；假如该节点的功能没有实现，那么令Gj=0（或pi=0）。对于某个结构中的一个节点Gj，我们定义以其为根节点相对应的功能树。同样的，功能树H（G1）函数用o/G1（X）=o/（p1，…，pn，G1…，Gk）表示（函数中的n，k代表是中间节点与叶子节点的个数）。在这个函数中，如果用户目标实现，也就是函数H（G1）中的根节点（G1）成立，那么得到o/G1（X）=1；如果用户目标没有实现，也就是函数H（G1）中的根节点（G1）不成立，那么得到o/G1（X）=0。接下来X（G1）用代表树形结构所有根节点和中间节点的全集。

定义2令FVMB=（bij）m×n，以B为根节点相对应的功能树为H（G1）（功能树中的各个节点G1，G2，…，Gk），G1，G2，…，Gk逐一对应于pn+1，pn+2，…，pn+k；对于功能树B，假设有k个分支，那么B［k］=（bij［k］）m×（n+k），B［k］定义成B的扩展矩阵。则，其中bij［k］∈{1,-1,0}（j=n+1,…，n+k）。

对于四值矩阵B，假设B为单行矩阵（B1×n=（bij）1×n），那么B定义为向量。假设矩阵对于B，当b1i=1（或b1i=-1）。另外，b1j=0（j=1，…，i-1，i+1，…，n），那么B1×n=α（α<-i>）；假设四值B矩阵为多行矩阵，α1,…，αm是矩阵B中的向量，假设则B=（α1,…，αm）T，用Z={1,-1,0，2}来表示。

定义3对于向量a1=（a1，a2，…，an），a2=（b1，b2，…，bn）（ai，bi∈Z，i=1，…，n）推出运算律如下：

“与”运算a1·a2，=（a1。b1，…，an。bn）=a，令a。a=a，0。a=a，2。a=2，1。-1=2（a∈Z）；

“或”运算a1+a2=（a1,a2）T；

“非”运算a1*=Bl×n。

假设l=Σ1

假如ai=1，可以得到α<-i>；假如ai=-1，可以得到α；假如ai=2，可以得到α和α<-i>；假如ai=0，则不做下一步运算。令B=（β1，…，βl）T，β1，…，βl分别是由其相对应的ai推出。

定义4对于四值矩阵B1=（α1，…，αm1）T，B2=（β1,…，βm2）T，令B1+B2=（α1,…，αm1，β1,…，βm2）T；B1·B2=（α1·β1，…，α1·βm，…αm·β1，…，αm·βm）；B1*=a1*·…·am。

令B［k］=（bij［k］）m×（n+k）=（α1，…，αm）T，设H0n+t={i|b［k］i，（n+t）=0}，H1n+t={i|b［k］i，（n+t）=1}，H-1n+t={i|b［k］i，（n+t）=-1}；B0n+t=（aq1，…，aqt0）T，B1n+t=（ap1，…，apt1）T，B-1n+t=（as1，…，ast-1）T。 显而易见{q1,…，qr0}=H0n+t，{p1,…，pr1}=H1n+t，{s1,…，sr-1}=H-1n+t（其中ap1，…，apt1，aq1，…，aqt0，as1，…，ast-1∈{a1,…，am}）。其中ai（aj）为xn+t对应的列是0时的值（令i=1，…，pr1，j=

下面的这个命题1描述了在与或非功能树展开过程，其相应的四值矩阵变化过程。

2.3 模糊功能树的保熵约简求解

熵，在热力学中是表示物质运动过程中混乱程度的计量单位，而在本文中熵表示模糊推理的创新性。所谓保熵，就是在模糊约简过程中保持推理的创新性不受到损失。在模糊推理过程中，推理的创新性取决于模糊原子公式的数量。在一个具体推导过程中，模糊原子公式个数确定，假设S={p1，…，pn}。F（S）所对应的合取式集合为Scj（S）。假设该合取式集合包含模糊原子公式，其定义为矛盾合取式Ccj（S）；假设该合取式集合不包含任何模糊原子公式，其定义为一般合取式Ncj（S）。在接下来的公式中，例如当A=f（p1，…，pn）时，本文p1，…，pn默认均在公式A中出现过。多个>的组合用Σ表示；多个>的组合用∏表示。

定义5对于四值矩阵B=（bij）m×n，假设Ebij=2（j∈{1,…，n}），其中Ek当bij≠0时bij=bkj（k∈{1,…，n},k≠i，Aj∈{1,…，n}），那么可以约简四值矩阵B的第i行（i=1,…，n），定义约简后的四值矩阵B1是原四值矩阵B的约简矩阵。

结合上面的推论，当进行概念设计过程中，使用模糊化后的模糊功能树能够表达功能实现的过程，再通过模糊推理进行逻辑运算。假设定义S={p1,p2,…}是模糊原子公式集，定义F（S）为模糊原子公式进行模糊推理的集合，推理过程主要运用>（析取）、（>合取）、（取反）、→（推导）四种运算。其中定理集合为1，矛盾式集合为0。当公式A为定理时，用|=A表示。对模糊公式进行约简，本文主要采用三种运算：

定义6下面这些模糊公式定义作模糊AND/OR式：g1=（其中x1∈{1，-1,0,2}代表不存在pi，pi∈S，i=1,…，n，这里的g1下标代表模糊公式具有的层次）（其中ki代表i层所含的因子数）；

如果“>”运算嵌套于“>”运算的外面，这一类的模糊公式定义为模糊OR-AND式；如果“>”运算嵌套于“>”运算的外面，这一类的模糊公式定义为模糊AND-OR式。基于此，得到上面定义6中的g2m+1是模糊OR-AND式，g2m是模糊AND-OR式，h2m是模糊OR-AND式，h2m+1是模糊AND-OR式。

定义7假设AQ∈F（S），那么可以得出Q可以转化为析取范式。其转换的过程有三个步骤：

步骤1：把Q中所有的逻辑关系转换为

步骤3：运用基本运算律将其转换为模糊AND/OR式。

假设中含有，则可以通过A>1≈1、A>0≈0、A>1≈A、A>0≈A将约简掉；在约简过程中自顶向下使用各种运算定律将原有公式转换为析取范式，可以将其定义成保熵析取式。

定义8令S1={p1，…，pn}，A=f（pi1，…，pim）∈F（S1），其中S2=SA={pi1，…，pim}（其中SA是模糊公式）

令S3=S1-S2，定义是F（S1）的衍生（其中xk∈{-1,0,1}）。所有衍生的集合定义为衍生集A（S1）。对于简单合取集U∩F（S1），假如，（其中x1，…，xm∈{-1,1}），设C1=D，对于所有C1组合{C1}，其在U中，即U（2）=U∩{C1}。我们设U（S1，j+1）=∩

A∈U（S1，j）（SN（S1，j））A（S1），算式至U（S1,BN（U，S1）+1）=U（S1,BN（U，S1））时停止。这样可以得到F（S1）范围内U衍生集是U（S1）=U（S1,BN（U，S1））。

在实际项目中，用户需求时有限的，因此本文排除无限集的可能性，结合以上定义8可以得到BN（U），SN（U）∈（0，+∞）以及BN（U），SN（U）∈（0，+∞）。综上得到以下引理1。

引理1设Q=（p1，…，pn），U为Q析取范式中析取项，当A∈U（SQ）时|=A→Q。

定义9若Q=（p1，…，pn），当A∈Scj（SQ）时，设A可以令|=A→Q，A∈U（SQ）（这里的U为Q中各组成部分的合集），则定义A是Q的最初方案，满足条件的最初方案合集我们记作OSS（Q）。

为了方便起见，把OSS（Q）矛盾合取式定义为COSS（Q），把OSS（Q）一般合取式记作GOSS（Q），可以得到OSS（Q）=COSS（Q）∩GOSS（Q）。

由此得到以下定理1。

定理1OSS（Q）=U（SQ），这里的U为Q中所有组成部分的合集。

定义10若A=f（p1，…，pn）∈F（S），B∈F（SA），假设B为A通过各项基本运算定律推导出的结果，则称B是A的约简。

定义11若A=f（p1，…，pn）∈F（SA），公式A里的则称作矛盾模糊公式，用pi*表示，的合集称为GA（A）。所有符合条件的模糊公式记作

接下来得到以下引理：

引理2若A∈F（S），B是公式约简，则OSS（B）（其中∩是“蕴涵”符号）。

引理3若A∈F（S），公式A中含有矛盾式，同时B是公式A内所有pi*通过约简，则我们可以得到OSS（B） ∩OSS（A）（其中 ∩是“真蕴涵”符号）。

引理4若A∈F（S），公式A中含有矛盾式C=pi*>C1（C=pi*），这里的C1是SA简单合取式，假设没有矛盾式D符合C=D（SA），当B为公式A约简，若约简使得保公式里不产生pi*>C1（或pi*），则可以得到OSS（B） ∩OSS（A）。

引理5若A=f（p1，…，pn）∈F（S），B=g（p1，…，pk），是公式A约简（其中k>0），则我们可以得到OSS（B） ∩OSS（A）。

引理6若A1=f（p1，…，pn），A2=g（p1，…，pn-k）是公式约A简（其中k>0），若T∩F（S），B1=h1（p1，…，pn，q1，…，qm，r1，…，rs）=T（A1）且B2=h2（p1，…，pn-k，q1，…，qm）=T（A2）（这里T在公式A1，A2中为同一运算，m，r>0），则我们可以得到OSS（B2） ∩OSS（B1）。

综合以上四个引理，本文得到定理2。

定理2对于公式A，如果其中没有0、1，且A=f（p1，…，pn）∈F（S），设B是公式A约简，假如在公式A约简过程中，模糊公式个数保持不变，则得到OSS（A）=OSS（B），B为公式A保熵约简。

综上所得模糊功能树的保熵约简算法（见图6）。

图6 保熵约简算法

其中，在保熵约简过程中如何消去矩阵重复向量的过程，可以参见图7中的保熵约简消除重复向量伪代码。

图7 保熵约简消除重复向量算法

尽管获得了模糊功能树的保熵约简，但是模糊功能树这种树形结构还不能直接运用于大数据环境下的实际项目运算中。针对这个问题，本文首先从模糊功能树总结出模糊功能函数，然后根据模糊功能函数构造模糊功能矩阵，接下来证明得到的矩阵与原先的树形结构是同构的，在接下来的研究中，我们可以通过矩阵运算代替树形结构计算。

第一步，构建功能函数，考虑到模糊功能树的现实定义，模糊功能树中的节点代表了功能的实现与未实现，与布尔函数的本质相同。例如X=（x1，x2，…，xn），这里的x1是模糊功能树中的分量，那么可以得到o/（X）=o/（x1，x2，…，xn）为由原有的树形结构得到的函数，用o/（x1，x2，…，xn）表示，在接下来的运算中用符号U简记，另外将所有公式合集定义为（U）。

从o/（x1，x2，…，xn）自顶向下逐步可以推出：U=将所有公式合集定义为。（U）。显而易见，这里

第二步，构建模糊功能矩阵可以从原来的树形结构根节点出发，按照自顶向下逐步得到树形结构中每一个节点相对应的模糊功能式，最后得到模糊功能树对应的模糊功能矩阵，详细的步骤见定义12：

通过定义12，本文完成了模糊功能矩阵的构造，接下来能够通过矩阵运算完成对模糊功能树的操作。

对于某个模糊功能矩阵B1×n=（bij）1×n，假设B1×n里的b1i=1（或b1i=-1），并且b1i=0（i∈{1，…，n}，j=1，…，i-1，i+1，…，n），则我们可以得到（或B1×n

对于某个模糊功能矩阵B，设其中各行变量是则可以得到B=（α1，…，αm）T。定义h（α）作为矩阵中各变量合集。令Z={1,-1,0,2}。

设α1=（a1,a1,…，an）,α2=（b1,b1,…，bn）∈h（α）（ai，bi∈Z，i=1，…，n）。定义如下三类操作：

(1)“或”操作：α1·α2=α，α（a1。b1，…，an。bn），2。a=2,0。a=a，a。a=a，1。-1=2（a∈Z）。

(2)“与”操作：α1+α2=（α1，α2）T。

(3)“否”操作：α1*=Bl×n。如果…，n）：

当ai=1时，得到α<-i>；

当ai=-1时，得到α；

当ai=2时，得到α、α<-i>；

当ai=0时，算法终止。

第三步，证明构造的模糊功能矩阵与原有的模糊功能树是同构的。

首先引入下面的命题。

定理3模糊系统同构。