回路压降冲激法的研究

焦运良 ，郑和芳 ，杨凯文 ，刘书萌 ，刘智国

(1.中电长城圣非凡信息系统有限公司，北京 102209；2.中国电子信息产业集团有限公司第六研究所，北京 102209)

0 引言

在电子电路应用场合，针对电路进行科学合理分析，才可以明确电路实现的功能。常见的电路基本分析方法有叠加定理、戴维南定理、支路电流法、节点电压法、网孔电流法、回路电流法等[1-2]。叠加定理和戴维南定理适用于求解某一支路的电流或某段电路两端电压；节点电压法适用于支路多、节点少的电路；回路电流法适用于线性电路等。按不同的电路方法列方程、解方程是电路分析的基本方法，同样的电路，采用不同方法得到的方程不同，求解的复杂程度也就不一样。为降低电路的分析复杂度和简化电路方程的运算过程，本文在回路电流法和线性叠加定理的基础上，提出回路压降冲激法，适用于线性网络，可大大减少电路的分析复杂度和简化运算过程。

1 叠加定理

在线性电路中，所有独立源共同作用产生的响应(电压或电流)，等于各个电源单独产生的响应的叠加[3]。在运用叠加定理时，需注意以下几点[4]：

(1)在考虑单一电源单独作用时，假设其他独立电源为零值，即电压源用短路替代，V=0；电流源开路，I=0；

(2)在考虑单一电源单独作用时，其参考方向选择与原电路中对应响应的参考方向相同，在叠加时用相应的数值代入，分电压和分电流的参考方向与其一致时取正号，不一致则取负号：

(3)叠加定理只能用于计算线性电路的电压和电流，而不能计算功率等和电压(或电流之间)无线性关系的参数。

以图1 为例，利用叠加定理求解电路中的电流I。首先根据图1(a)中的原电路，画出其叠加定理的等效电路图如图1(b)和图1(c)所示，两个独立电压源作用叠加之后计算得出I 的电流值。

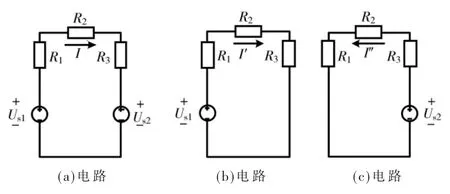
图1 叠加定理

Us1电压源单独作用时：

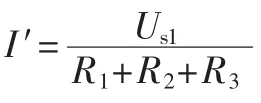
Us2电压源单独作用时：

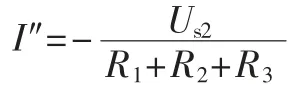
则求解得出原电路图1(a)中的电流I：

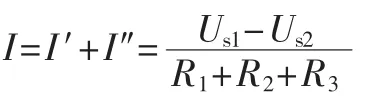
从上述的求解过程中可以看出，叠加定理适合在一些简单的线性电路中使用，求解过程也是较为简单的。

2 回路电流法

回路电流法是以一组独立的回路电流为电路变量，再根据电路定理列电压方程的电路分析求解方法[5]。其中，在任意时刻，电路中各回路压降之和为零。求解的步骤分为：选择回路，确定回路的绕行方向；根据所选回路列写电压方程；解方程，求得所需的回路电流值[6]。

以图2 为例，各电阻阻值及电源电压已知，求电源U2中流过的电流I。

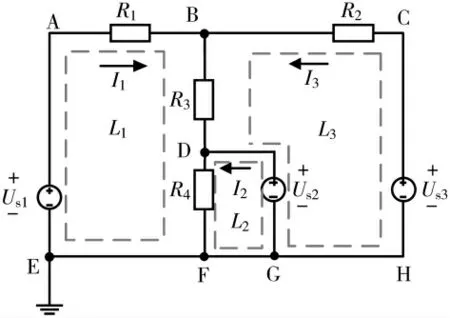
图2 回路电流法

该电路网络结构可选BDF 为树，则由它的3 个连支将其分成3 个回路[7]，如图2 所示，依次为：L1(A-＞B-＞D-＞F-＞E-＞A)、L2(D-＞G-＞F-＞D)、L3(B-＞C-＞H-＞G-＞D-＞B)；设各回路假想电流分别为I1、I2、I3，方向均为顺时针。根据回路电流法列方程组如下：

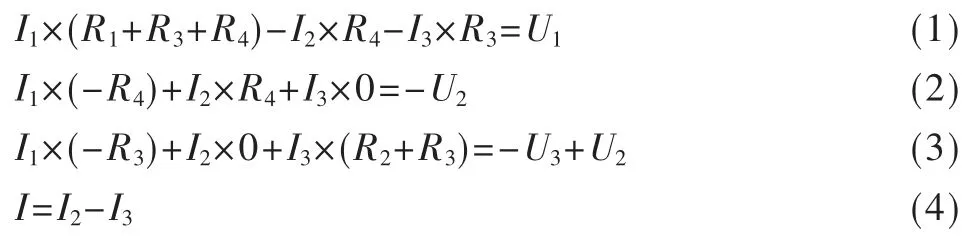
根据上面的方程组，运用相关的数学方法便可以求解方程组，得出I 值。

从上述的求解过程可知，回路电流法需要建立的方程个数与回路网格数一致，方程个数较少，运算量也不多，但是并不适合很复杂、网格数多的电路。

3 回路压降冲激法

3.1 思想

根据上面对叠加定理和回路电流法的介绍与分析可知，利用回路电流法求I 时，需要解3 个独立的方程，求解过程相对较为复杂[8]。在回路电流法的分析中，以独立电源(包括假想的)作为关键变量，重点分析各独立电源(简称独立源)对回路产生的冲激压降[9]。其核心思想也是根据基尔霍夫电压定律来列电路的电压方程，即电路网络中任一回路压降之和为零[10]。这也是本文介绍的回路压降冲激法依据的电路原理之一。

而在线性叠加定理的分析中，回路的最终状态是各个独立源单独作用的叠加[11]。如果把待求的未知量(如前例的电流I)也看作一个独立源(假想的独立源)，根据各个独立源单独作用电路，同样可以求出I 的电流值。

综合考虑上面两者方法的特点，结合两者的优势，提出一种回路压降冲激法。在回路电流法电路分析中，某一回路中所假想的电流相当于待求量，则该回路的独立源相当于内独立源，而对于其他回路电流相当于外独立源[12]。再根据内外独立源和待求量分别对电路产生的冲激压降之和为零这一基本原则，列和解方程。因此利用此文提到的方法，只需求解各独立源产生的冲激压降，便可以求解得到待求量的值。对比单独使用回路电流法，此方法明显减少了回路网格数和运算的方程数，简化了电路的复杂度。

3.2 用回路压降冲激法进行电路分析

回路压降冲激法的基本思想是根据电路中的独立源及待求量设为关键变量，同时选定回路，依据三部分冲激压降和为零，由单位待求量冲激压降求出待求量[13]。

首先假设组成回路的三部分冲激压降：内独立源压降、外独立源压降和待求量压降，分别为U内、U外和U待，如果待求量压降与回路方向相同时取正；内独立源压降、外独立源压降与回路方向相同时取负，则有∑U待=∑U内+∑U外。设单位待求量的冲激压降为∑UI，则待求量X待=(∑U内+∑U外)/∑UI。

因此，分析和求解过程如下(注：各变量求取时，除源后电路结构不改变，各独立源仅能通过回路外器件对回路产生冲激压降。)：

(1)选定回路。选定的回路要含有待求量，方向可自定。根据回路的方向确定各独立源的正负。

(2)待求量及回路内独立源除源(电压源短路、电流源开路)，求外独立源对回路的总冲激压降∑U外。

(3)外独立源及待求量除源，求内独立源对回路的总冲激压降∑U内。

(4)内、外独立源除源，求单位待求量对回路的冲激压降∑UI。

按照上述过程，用回路压降冲激法分析图2 电路。电压源U2中的电流I 为待求量，可选取L 回路，如图3 所示，方向为顺时针。则内独立源为U1、U2，外独立源为U3。

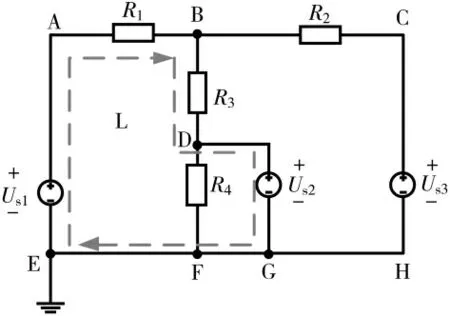
图3 回路压降冲激法

内独立源冲激压降(待求量I、外独立源U3除源)：内独立源U1、U2，不仅是回路的一部分压降，而且还通过回路外元件R2、R4对本回路内电阻R1、R3产生压降。

首先求解内独立源自身压降U内。内独立源U1与回路方向相反，取正；U2方向相同，取负。所以U内1=U1-U2。

对于U1，因为两端没有直接并联任何回路外元件，所以对本回路内电阻不会产生额外压降；对于U2，两端连接R4，所以R4中激励电流为U2/R4。对待求量I 除源，即U2中电流为零，故R3中电流与R4相同，其方向与回路L 相同，取负，故R3上压降为：

BF 两点间电压为：

由于U3除源，故在R2中激励的电流为UBF/R2。R1中电流为R2、R3两支路之和，方向与回路方向相同，取负，所以R1压降为：

由A、B 得内独立源冲激压降：

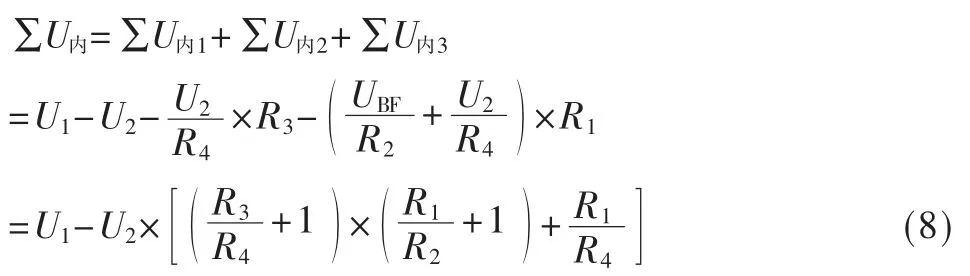
其次求解外独立源冲激压降(待求量I 及内独立源U1、U2除源)。U2除源使得R4中的电流为零，而待求量I又为零，所以R3中的电流为零，进而UBF=0。U3通过R2对回路冲激的电流为U3/R2，直接流向R1，与该回路方向相反，故取正，R1上得到的压降为(U3/R2)×R1。则外独立源压降∑U外=U3×(R1/R2)

最后求解待求量冲激压降(外独立源U3及内独立源U1、U2除源)。U2除源使得R4中电流为零(R4两端电压为零)，则R3中的电流为I，故UBF=I×R3。UBF在R2中产生的电流为UBF/R2，R1的电流为R2、R3之和，故其压降为方向与回路相同，取正。因此，待求量压降为：

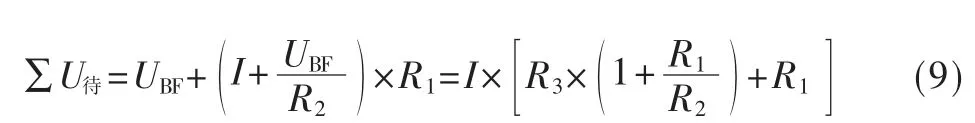
单位待求量压降(I 为1 时的压降)为：

代入公式得待求量I 的值：

如上所述，利用回路压降冲激法分析电路，避免了解方程组的麻烦，只需分析各独立源分别对电路产生的冲击压降，再数学代入相应的变量之中，最后只需一个方程便可以求解；对应于回路电流分析方法，也减少了多个回路网格的列方程求解，简化了运算量，同时还加深对电路的工作本质的理解。

3.3 电路分析方法对比

支路电流法是以基尔霍夫电流和电压定律为基础，各支路节点电流之和为零，各回路电压之和为零，列方程求解所求量的电路分析方法[14]。求解步骤如下[15]：

(1)标明电路的各支路的电流参考方向和电流；

(2)列出节点数N，支路数b；

(3)根据节点数列出N-1 个独立的电流(电压)方程；

(4)选取回路，规定绕行方向(尽量选取网孔回路)，利用基尔霍夫电压定理列出[b-(N-1)]个独立方程，每条支路上的电流参考方向与绕行方向一致为正，否则为负；

(5)联立组成方程组并求解，得出各支路的电流值。

以支路电流法和回路压降冲激法分别分析一个带有反馈的放大电路为例，说明本文提到方法的特点。

电路原理图如图4 所示，已知各电阻的阻值及输入电压Us，求输出电压Uo。

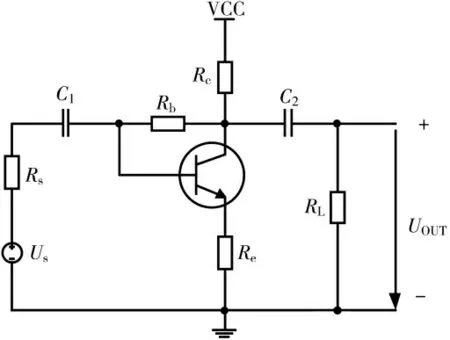
图4 电压并联反馈放大电路

利用支路电流求解时，其微变等效电路图如图5所示。

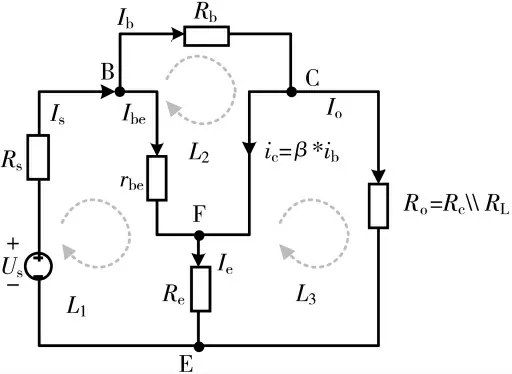
图5 微变等效电路a

根据图中所选取的回路L1、L2和L3，以及B、C、E、F各个节点，列出回路的电压方程和节点的电流方程组如下。

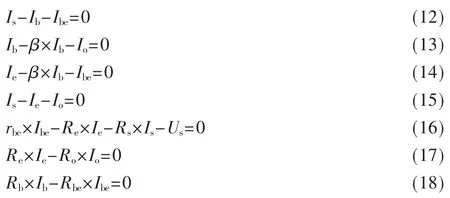
联立上述的7 个方程构成方程组，便可以求解出各支路的电流，同时计算出输出的电压值Uo=Ro×Io。该过程相对复杂，方程的个数也是较多，计算起来并不简单。因此只适合一些简单的线性电路。

利用回路压降冲激法时，微变等效电路图如图6 所示。选输出电压Uo为待求量，选定回路L1(A-＞B-＞C-＞D-＞E-＞A)，则内独立源为Us，无外独立源，且方向与回路相反，故内独立源回路冲激压降∑U内=Us。待求量对回路的冲激压降由待求量在回路电阻Rb、Rs上产生的压降及待求量本身Uo组成。

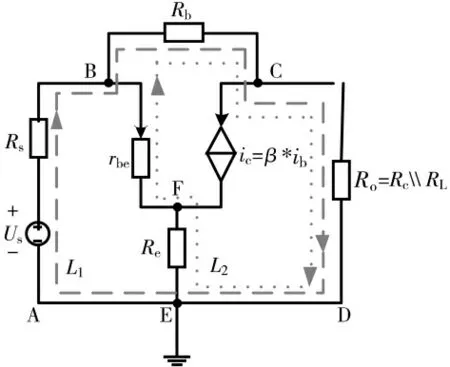
图6 微变等效电路b

电阻Ro中电流Io=Uo/Ro。Rb中的电流由Io、ic两部分组成(节点C)，所以Rb上的电压为Rb×(Io+ic)，即Rb×(Io+β×ib)。Rs中的电流由Rb中的电流与ib两部分组成(节点B)，所以Rs上的电压为Rs×[Io+(β+1)×ib]。分别计算外独立源冲激压降：∑U内=0；内独立源冲激压降：∑U内=Us，最后求得待求量冲激压降为：

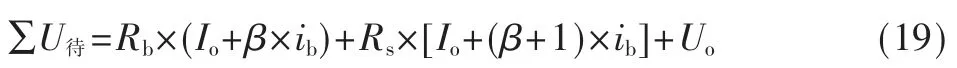
式中含有未知量ib，求解ib。选L2(B-＞C-＞D-＞E-＞F-＞B)回路，ib为L2回路的待求量，Uo为内独立源，而Us为外独立源。

待求量冲激压降：Re中的电流为(β+1)×ib，内独立源Uo除源使得Rb中的电流为β×ib(节点C)，待求量与回路方向相反，取负，则：

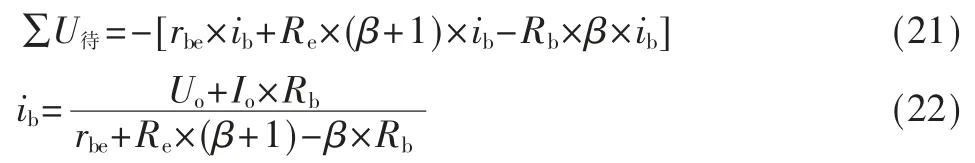
将式(22)带入式(21)中，得到：

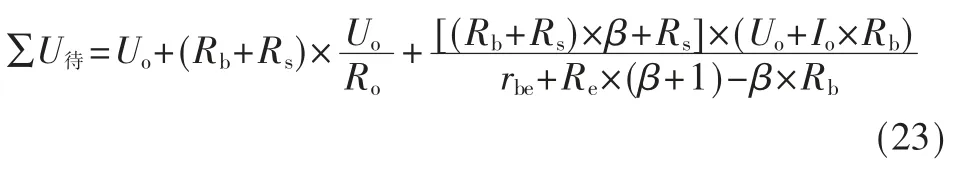
单位待求量(Uo=1)对回路L1产生的冲激压降为：

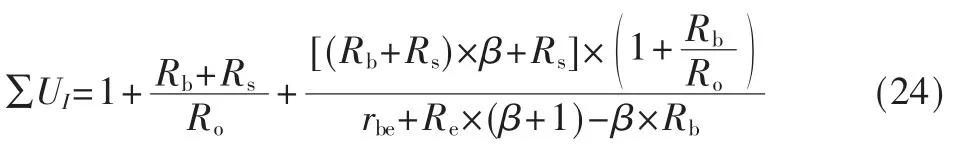
据此求出输出电压：

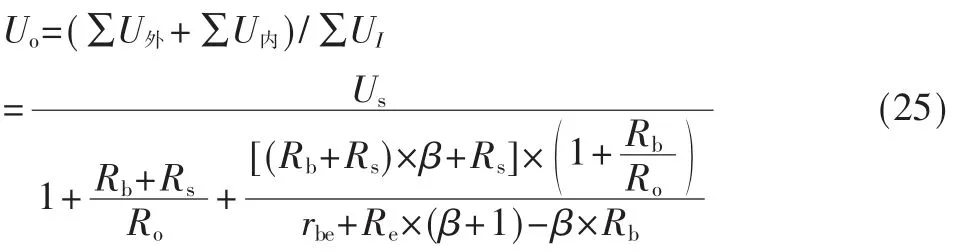
上述的求解过程相对容易，就是以内外独立源和待求量的压降冲激之和为零的基本原则为准，列出方程分别求解这三个电压值，进而得到输出电压值。因此，回路数更少，所列方程数相应减少，运算量也得到简化，适合于复杂的线性电路分析。经实验统计可知，运算量相比支路电流法减少20%。

4 结论

回路压降冲激法是在叠加定理和回路电流法的基础上，集合两者的优势，简化了电路的复杂程度，仅以各独立源的回路压降冲激为变量，就可以计算所求量。此方法的显著特点是回路少，方程数简化，使得运算量也相应减少，这在一些较为复杂的线性电路中可以得到很好的运用，并且对于深入理解各元件间的相互作用及设计电路有很好的指导意义。