基于时空卷积神经网络的智能电表故障预测

高文俊，薛斌斌，庞振江

(北京智芯微电子科技有限公司，北京 102299)

0 引言

我国电网从“信息化”向“智能化”发展是未来的必然趋势[1]。智能电表是智能电网数据采集的基本设备之一，承担着原始电能数据采集、计量和传输的任务，是实现信息集成、分析优化和信息展现的基础。近年来，随着智能电网信息采集系统的建设，智能电表已经获得了大范围的推广和应用。如此大规模的智能电表一旦出现故障，会影响到电网的控制和管理，与人民的切身利益和社会的和谐稳定密切相关[2-3]。

目前，国内主要是通过定期巡检的方式确定电表的故障信息，并作进一步处理。但是该方法需要耗费大量的人力、物力和时间资源，并且需要巡检人员具备一定的专业知识[4]。随着我国科技的快速发展，越来越多的智能电表数据被采集和存储，采用数据挖掘的方法对智能电表的故障数据进行特征提取，捕捉各特征间的影响规律，实现对智能电表的故障预测成为未来发展的重要方向[5]。

近年来，关于智能电表的故障预测研究仍处于初步阶段。文献[6]采用一种基于聚类分析和云模型的智能电表故障分类方法，但是聚类的方法很难定义故障的种类。文献[7]采用基于评分搜索的方法构建了贝叶斯网络结构，在此基础之上对智能电表的故障进行预测和决策分析。但是贝叶斯网络对输入数据的表达形式敏感，当属性个数较多或属性之间相关性较大，数据量较大时，分类效果会受到影响。文献[8]通过人为删除重复数据与无关数据，补全数据中的缺失值，获得预测数据和特征数据，采用神经网络的方法对智能电表的故障类型进行分析。该方法可以良好地针对海量数据进行建模，但是需要先对数据的输入特征和无关数据进行人为处理，人为选择的相关特征很有可能会舍弃掉一部分有用的数据信息，使故障预测精度受到影响。

卷积神经网络相比于传统的BP 神经网络、SVM 等算法[9-10]，更适用于高维数据，具有更强的特征捕捉能力，目前在诸多工业领域都有良好的表现[11-13]。

考虑到智能电表故障呈现出的动态性、复杂性、多面性等特点，本文提出了一种基于时空卷积神经网络的智能电表故障预测模型，该模型将时间信息融入特征变量中，构建具有时空特性的输入矩阵，并与卷积神经网络相结合，实现对智能电表故障的准确预测。通过实例验证，本文提出的模型具有较高的预测精度，对于实现智能电表的故障预测是合理有效的。

1 基于ST-CNN 智能电表故障预测的研究

1.1 基于ST-CNN 智能电表故障预测模型建立

考虑到智能电表故障呈现出的动态性、复杂性、多面性等特点，本文提出基于ST-CNN 的智能电表故障预测方法，其预测流程如图1 所示。

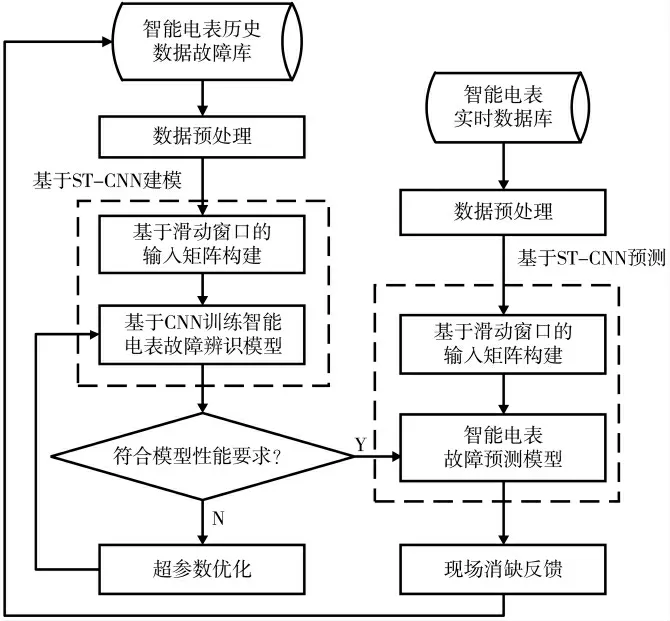
图1 智能电表故障预测流程

首先对智能电表历史数据做预处理，包括基于中值滤波的异常值处理和归一化；然后基于滑动窗口将时间信息融入输入数据中，构建具有时空特性的输入矩阵；并与CNN 相结合建立智能电表故障辨识模型，通过超参数优化的方法保证模型性能达到预设要求；最后，在此基础之上，对实时数据进行故障预测，并与现场消缺反馈相结合，补充历史故障库，实现预测模型的实时优化与校正。

1.1.1 数据预处理

考虑到采集数据中异常值的存在会对模型精度造成影响，本文采用中值滤波的方法对特征变量进行异常值剔除。

设o=(o1，…，oi，…，on)为智能电表某变量的时间序列数据，on表示第n 时刻该变量的值。设窗口长度为2K+1，K 为整数。那么对oi进行中值滤波就是从变量o中抽取出2K+1 个数，表示为：oi-K，…，oi，…，oi+K，其中，i为窗口的中心位置；再将抽出的2K+1 个数按照数值大小进行排列，选取中间位置的数据，数学表达式如式(1)所示：

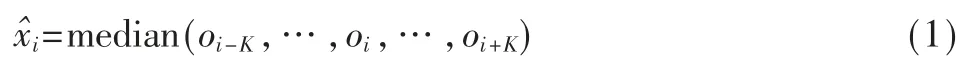
1.1.2 基于滑动窗口的输入矩阵构建

现有智能电表故障预测研究往往忽略特征变量的时间特性，时间序列数据可以包含更多的有效信息，提高故障预测的实时性和准确性[14]。本文采用滑动窗口的方法对每个特征变量的时间信息进行选择，获得输入矩阵，如图2 所示。

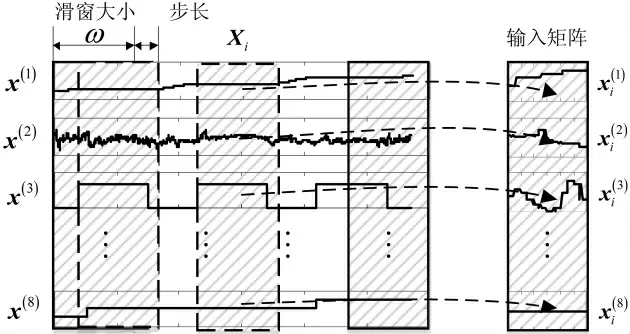
图2 基于滑动窗口的输入矩阵构建

1.1.3 基于CNN 的故障预测模型建立

CNN 是一种人工神经网络，不同于MLP，它考虑了输入数据的空间关系，可以更好地捕捉多变量间的非线性相关性[15]。本文结合智能电表故障预测模型，介绍CNN 算法的基本思想。

本文采用的CNN 结构为2 个卷积层、2 个池化层和1 个全连接层，如图3 所示。

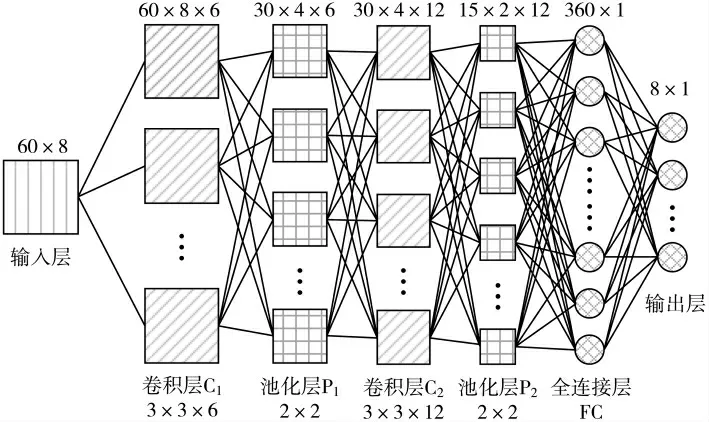
图3 本文所用CNN 网络结构

已知构建的输入矩阵X 为输入变量，对应的故障类别Y 为输出变量。CNN 的训练过程主要包括正向传播和反向传播。

(1)正向传播：

卷积层C1的传播过程如下式所示：

式中，fC2(·)表示ReLU 激活函数。

池化层P2的传播过程如下式所示：

全连接层的作用则是对提取的特征进行非线性组合以得到输出，特征图在全连接层中会失去空间拓扑结构，被平铺(Flatten)为向量，如下所示：

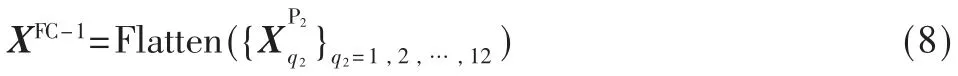
则全连接层输入为XFC-1，全连接层的正向传播过程可以表示为：

式中，WFC表示全连接层权重，bFC表示全连接层偏置，表示预测的故障结果，fFC(·)表示sigmoid 激活函数，fFC(x)=

(2)反向传播

损失函数如下式：

式中，N 表示训练样本个数，Y＾表示模型预测结果，Y 表示实际结果。

CNN 的反向传播就是对参数WFC、bFC、的迭代更新，本文选用Adam 优化方法对模型参数进行更新[16]。

1.1.4 模型性能评价标准

本文采用准确率(Accuracy)、精确率(Precision)、召回率(Recall)和综合评价指标F1 共同作为智能电表故障辨识模型的评价标准。

分类评价指标的定义：TP(True Positive)表示将正类预测为正类数，TN(True Negative)表示将负类预测为负类数，FP(False Positive)表示将负类预测为正类数，FN(False Negative)表示将正类预测为负类数。

准确率(Accuracy)的计算公式如式(11)所示：

精确率(Precision)的计算公式如式(12)所示：

召回率(Recall)的计算公式如式(13)所示：

综合评价指标(F1)的计算公式如式(14)所示：

1.2 基于ST-CNN 智能电表故障预测的算法研究

由节1.1 可知基于ST-CNN 智能电表故障预测的具体流程，本节对基于ST-CNN 的智能电表故障预测算法进行具体描述。

(1)通过智能电表故障库获得故障相关特征变量o=(o(1)，o(2)，…，o(s))，输出故障类别Y。其中，s 表示特征变量个数。

(3)将时间信息融入到x 中，根据式(3)构建输入矩阵X。

(4)将X 作为输入，根据式(4)～式(9)进行CNN 前向传播，得到输出结果。

(5)根据式(10)计算模型损失函数，并采用Adam 优化算法对模型参数进行更新，得到智能电表故障辨识模型。

(6)根据式(11)～式(14)建立模型评价标准，当该4 个标准均大于85%时，保存模型参数，获得智能电表故障预测模型；如果不满足预设要求则继续进行参数优化，直至满足要求为止。

(7)对于实时数据，根据式(1)～式(3)构建输入矩阵，并放入训练好的故障预测模型中，对故障类别进行实时预测。

(8)现场人员根据预测结果进行实时消缺和反馈，并将数据放入历史故障库，对故障预测模型进行实时的参数更新。

2 智能电表故障预测试验

2.1 样本数据选取

本文选择某公司智能电表故障库中的故障数据，故障类别共8 类，分别是：正常、采集异常、电表示值不平、电表飞走、电表反向有功示值异常、电表倒走、电表时间异常和电表潜动异常。

智能电表故障相关数据共8 种：包括总电量数、峰段电量数、平段电量数、谷段电量数、电流、电压、电表时间、终端时间。

数据的采样频率为每秒1 个点，选择智能电表分别处于8 类故障时，运行30 min 的数据作为原始数据，共14 400 个点。选择前20 min 的连续数据为训练原始数据，共9 600 个；选择后10 min 连续数据作为预测原始数据，共4 800 个。

2.2 输入矩阵构建

滑动窗口的大小选择为1 min，即60 个连续数据点，步长选择为1。选择8 个与智能电表故障相关的变量，所以，输入矩阵可以构建为60×8 的矩阵。

将每个输入矩阵与对应的故障类别作为一个样本，获得样本数据共14 280 个，其中训练样本9 540 个，预测样本4 740 个。

2.3 时空卷积神经网络模型结构

本文采用的时空卷积神经网络模型结构见表1 所示，共采用2 个卷积层、2 个池化层、1 个全连接层。学习率设置为0.001，第一次估计的指数衰减率为0.9，第二次估计的指数衰减率为0.999，训练轮数设置为1 000 次。

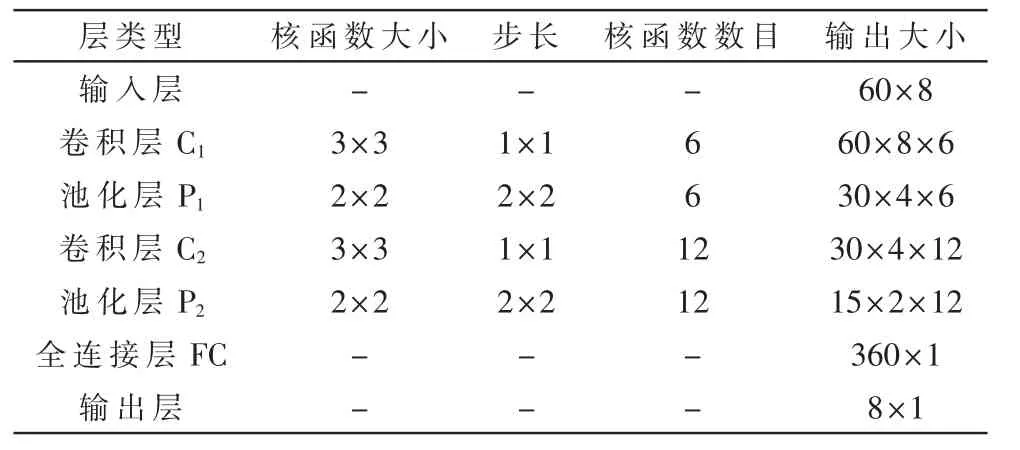
表1 时空卷积神经网络模型结构

本文采用的核函数是3×3，这是因为3×3 是最小的能够捕获像素八邻域信息的尺寸，而且多个3×3 的卷积层比一个大尺寸卷积层使用了更多的非线性激活函数，判决性更强，同时使用的参数更少，模型复杂度更低。

本文采用3×3 核函数堆叠的方法对模型结构进行试凑，当模型具有2 层卷积层时，模型精度已经可以满足故障预测的需求，过高的层数在模型精度提升并不大，同时会造成大量的计算冗余。

2.4 智能电表故障预测结果

本文将目前智能电表故障预测常用的BP 神经网络、随机森林、SVM 和朴素贝叶斯模型与本文方法作对比，结果如图4 所示。

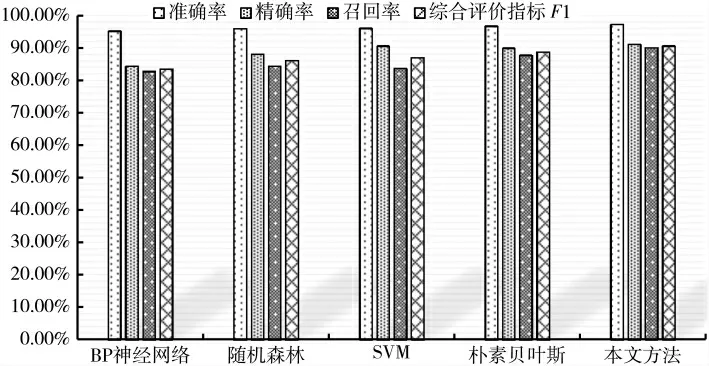
图4 智能电表故障预测多模型对比

表2 给出了本文方法与其他4 个常用模型的预测结果对比。从表2 可以看出，本文方法与其他4 个模型相比，无论是在准确率、精确率、召回率，还是F1 评价指标，都是表现最好的模型，这也说明了本文算法的有效性。

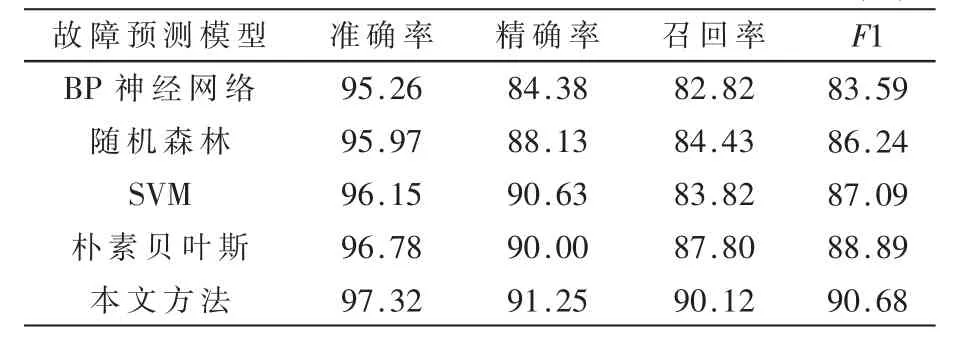
表2 智能电表故障预测多模型对比(%)

从表2 可以看出，朴素贝叶斯的召回率高于SVM，但是精确率低于SVM，随机森林的召回率高于SVM，但是精确率低于SVM。这说明采用4 种不同的评价标准，从不同的角度对模型进行综合判断才能更准确地对模型性能进行评价。

表3 给出了本文所采用的方法在8 种故障的预测结果。从表3 可知，采集异常与电表示值不平这2 类故障预测准确率较低，其他故障的预测准确率相差不多，其中，电表反向有功示值异常预测准确率最好。

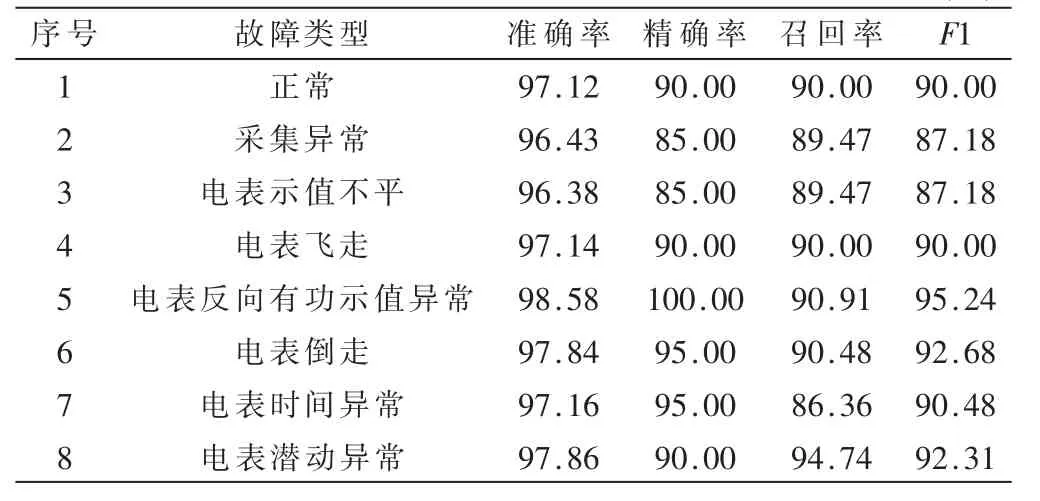
表3 本文方法各故障的预测结果 (%)

导致某类故障预测准确率较低的原因有很多，后续可以针对预测准确率低的故障开展详细研究，找到准确率低的具体原因，通过输入特征的修改和模型结构参数的调整提高模型的整体性能。

3 结论

本文采用滑动窗口的方法将时间信息融入输入变量中，并结合CNN 捕捉数据的时空特性，提高了模型的精度和实时性。仿真结果表明，本文提出基于ST-CNN智能电表故障预测模型的准确率、精确率、召回率、F1均高于其他4 种对比模型。准确的预测智能电表故障不仅可以为现场运维人员提供数据参考，同时也可为电网的控制和管理提供理论和技术支持。