10-16 位旋变数字转换器中Sigma-Delta 调制器设计*

谷 军 ，张国华 ，朱晓宇

(1.江南大学 物联网工程学院，江苏 无锡 214000；2.中国电子科技集团第五十八研究所，江苏 无锡 214000)

0 引言

随着VLSI 技术的高速发展，集成电路的速度已然不再是设计中的短板，以速度换取精度成为了转换器设计中的共识，过采样技术也成为了转换器中最为广泛采用的技术之一。Sigma-Delta ADC(Σ-Δ ADC)最早出现于1962 年，是使用广泛的过采样ADC，它是所有电路非理想性的最稳定的ADC。Σ-ΔADC 在目前大多数字混合系统中占有重要地位，例如模拟电路与强大的数字处理环境之间的接口电路[1-3]。它们最适于慢速和中速转换,例如检测装置、数字语音和音频应用。与奈奎斯特ADC 相比，Σ-ΔADC 主要增加了Σ-Δ 调制器与数字抽取器，后者占据了大部分ADC 芯片面积，比调制器消耗更多的功耗[4]。输入信号经过采样保持电路送入调制器中，在调制器中信号被转换为数字码流，该数字码流经过低通滤波器滤除高频噪声并将其采样率降至奈奎斯特频率，得到最终数字输出。调制器完成采样及量化的功能[5]。本文研究的目的是为10-16 位旋变数字转换器设计一种可靠的Σ-Δ 调制器，优化其性能。

1 Σ-Δ 调制器原理

对于一阶调制器来说，采样率每提高一倍，其分辨率可增加1.5 位，这就意味着为了实现高分辨率，必须使用相当大的采样率。另外，某些情况下，一阶调制器的输出频谱整形效果很差，并且可能会产生落入信号频带内的噪声分量[6]。在环路中使用两个积分器可以获得更好的性能，从而形成二阶调制器。本文面向数字转换器设计的调制器为二阶，其二阶Σ-Δ 调制器原理由图1所示。

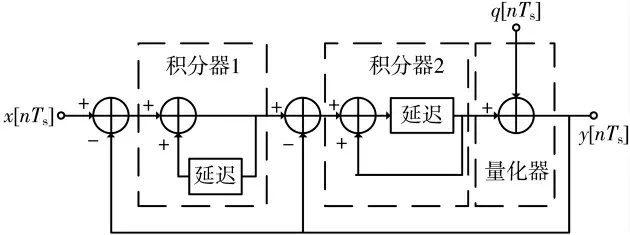
图1 二阶Σ-Δ 调制器模型

二阶调制器是由一阶调制器在前馈支路中增加一个积分器扩展而成的。积分器的传递函数H1(z)=第二个积分器包括一个延时单元，则其传递函数H2(z)=，通过观察函数，可以得到以下式(1)～式(3)：

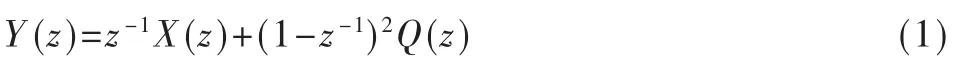
调制信号与噪声的传递函数可以用以下公式表示：

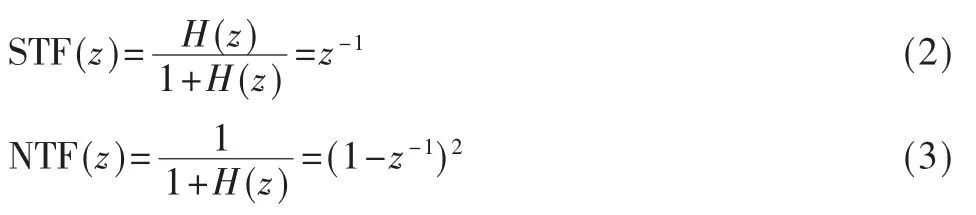
在调制器设计中STF(z)等于1，或者至少在信号带内等于1，从而信号可以不经过衰减通过调制器，NTF(z)在带内被设计成具有衰减效果。从两个传递函数可以看出，调制器对输入信号只是起到了延迟作用，因此有用的信号可以无损地传输[7-8]。

2 Σ-Δ 调制器的设计

2.1 调制器的整体设计架构

Σ-Δ ADC 是一种过采样的数模转换器，它的采样频率远大于信号的奈奎斯特频率，以时间的精度换取幅值的精度。量化噪声在信号带宽内的大小决定了过采样ADC 的精度，量化噪声谱均匀分布在[0，fs/2]之间，因而采样频率fs越大，信号带宽内的噪声功率越小，使得量化噪声在信号带宽内稀释，从而提高过采样ADC 的精度[9-11]。Σ-Δ 调制器对量化噪声进行整形，对量化噪声来说形成一个高通滤波器，这样信号带宽内的量化噪声在过采样技术的基础上继续减少。本文面向旋变转换器设计的Σ-Δ 调制器原理图如图2 所示。

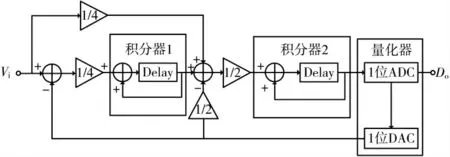
图2 转换器中Σ-Δ 调制器原理框图

通过以上原理图可知，转换器中的调制器采用2 阶单环路1 位量化器系统结构，其中两个积分器实现2 阶调制器，量化器由1 位的ADC 与DAC 结构组成。积分器实现将有用的低频输入信号通过高频时钟调制至高频，通过数字滤波器把处于高频的量化噪声滤除，有效信号恢复至低频的功能，再经过数字抽取滤波之后即可以完成整个ADC 的功能[12-14]。

为保证调制器的信噪比并避免谐波失真的关键是必须在运算放大器中采用合适的动态范围，一方面运算放大器的摆幅不能太高以引起饱和，另一方面也不能低到与电子噪声相当的程度，所以按一定的比例适当地衰减(或放大)积分器的输入，通过在下一级的输入端进行反过来放大(或衰减)来补偿。因为衰减和放大相互抵消，运算放大器的摆幅得到优化，在本文设计的调制器中的电路的实现方式为通过积分器的比例实现[15]。

根据图2 原理图得到输入输出的关系如式(4)所示：

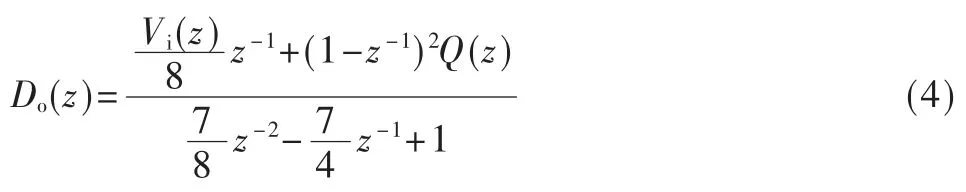
2.2 新增斩波电路滤除闪烁噪声

闪烁噪声是因为电荷载流子运动到晶体管的栅氧化层和硅衬底的界面产生，而且随着CMOS 工艺步骤的增加和特征尺寸的减少，闪烁噪声越来越大。目前降低闪烁噪声的方法主要有：自调零技术、相关双采样技术和斩波稳定技术。本文采取的方法为斩波稳定技术，因为在理想情况下，斩波稳定运放应能完全消除直流失调和闪烁噪声，对于连续信号，斩波电路的调制解调方法更好地减小闪烁噪声。本文设计的斩波调制电路如图3所示。

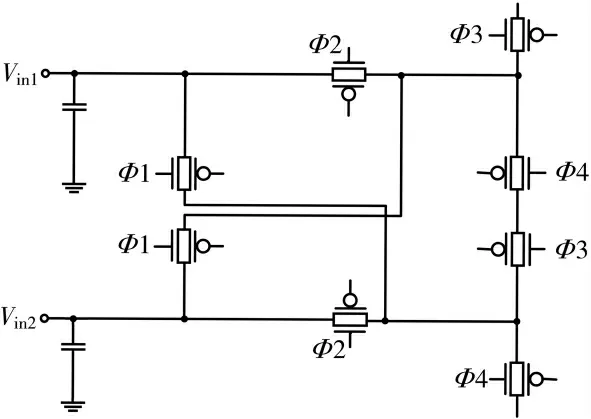
图3 斩波调制电路

根据图3 所示的斩波电路，在本文设计调制器中作用原理为：输入是差分信号的正弦波，通过调制器，输入信号被调制到时钟信号(图中Φ1-Φ4)的谐波频率上，而后由相同的方波解调信号解调，这样闪烁噪声只被方波调制信号调制到高频，从而与量化噪声最终低频滤波器滤除。

2.3 不重叠时钟电路

不重叠的时钟电路是为了控制斩波电路与积分器的工作状态，对斩波电路来说，四组时钟信号处理斩波的调制与解调，由于实际操作中的非理想因素，不重叠的时钟没法实现完全一致的反相状态，这将导致电荷传递会有误差，积分器功能没有办法正常实现。并且对积分器来说，如果两相时间间隔太短，可能会造成延时时钟的重叠。但时间间隔也不能太长，否则会引起系统错误，导致系统的误差增大。与此同时，电路的其他时序会难以满足，并可能出现电荷泄露的现象，这不仅降低了电路的集成精度，还会导致电路的非线性效应。与斩波电路不同的是，处理积分器的时钟信号频率不同，斩波电路的时钟频率约是积分器时钟频率的2 倍，由于各相的结构相同，因此在这里只呈现其中一相的时钟电路设计图，如图4 所示。

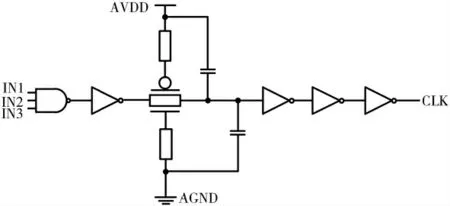
图4 时钟电路

积分器的时钟频率与斩波电路的时钟频率在电容值与数字寄存器配置的三输入与非门控制信号的频率不同，导致两者频率的不同。

3 Σ-Δ 调制器的建模与仿真

根据积分器在积分相和采样相的电压转换关系，可以VerilogA 模型取代原电路实现仿真加速，同时可以分析该调制器在该模型下的FFT 波形。激励条件为：输入3.15 Vpp，频率为2.1 kHz，共模信号为2.47 V 的正弦信号到该模型中，采样点为32 768，信号带宽为20 kHz。VerilogA 模型仿真得到的FFT 波形如图5 所示。

由图5 所知，在20 kHz 带宽下得到的Σ-Δ 调制器的有效位数为13，信噪比为80 dB。同样，对于该调制器电路，搭建MATLAB 模型，分析该调制器在MATLAB 模型下的FFT 波形，并与VerilogA 所分析的结果做对比。根据调制器的结构搭建如图6 所示的MATLAB 模型。

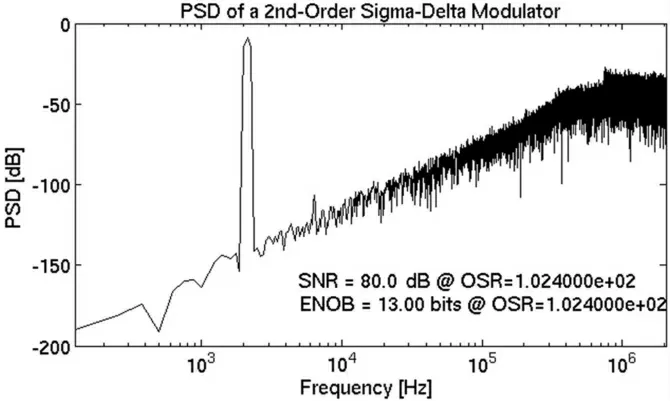
图5 VerilogA 模型仿真频谱图

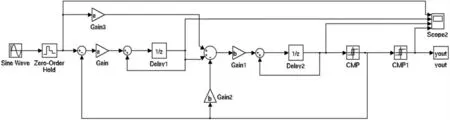
图6 Σ-Δ 调制器的MATLAB 模型

其中a=1/4，b=1/2，通过对其转换码流进行FFT 分析，可以得到频谱图，如图7 所示。

图7 MATLAB 频谱分析

通过MATLAB 与VerilogA 仿真可以发现两频谱图得出的结果一致。

而本文面向10-16 位转换器设计的Σ-Δ 电路输入带宽会根据所配置的求解精度而不同，根据Spectrum 说明，转换器在不同分辨率下对激励频率有一定要求，10、12、14、16 位分辨率对应的激励频率范围不同，因此Σ-Δ调制器输入信号带宽也会发生改变，其对应关系如表1所示。

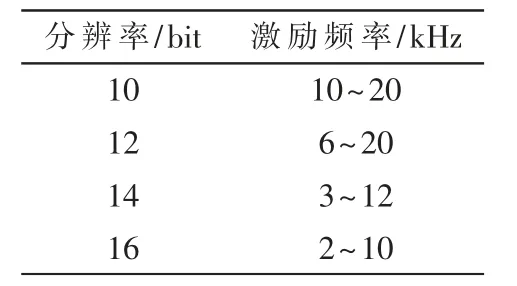
表1 Σ-Δ 调制器信号带宽与分辨率关系

对VerilogA 模型产生的码流在不同的带宽下做FFT 分析，其频谱输出如图8～图10 所示。

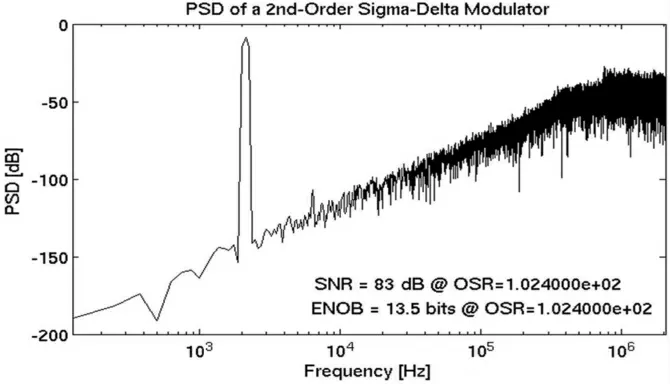
图8 带宽为20 kHz 的FFT 求解

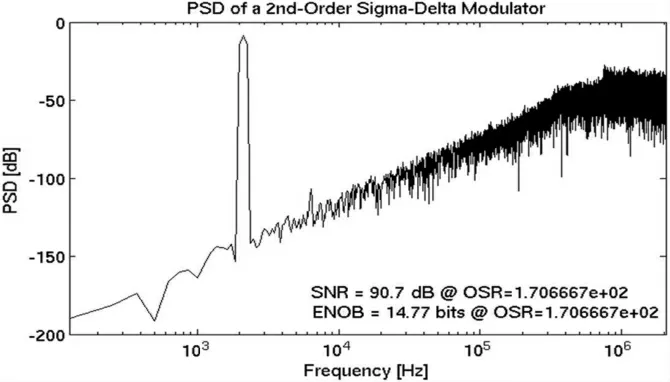
图9 带宽为12 kHz 的FFT 求解

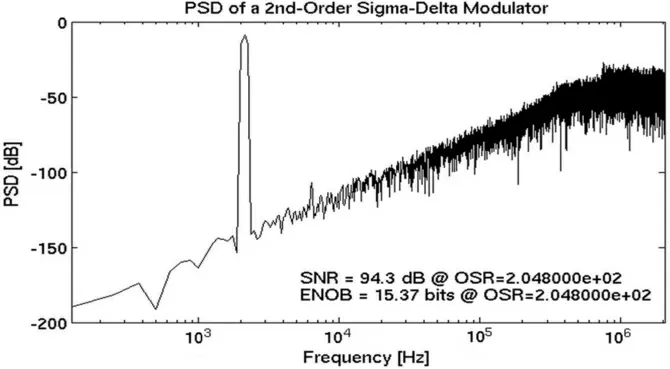
图10 带宽为10 kHz 的FFT 求解

根据以上频谱图分析得到表2 所示结果。

根据表2 的仿真结果得出结论，该调制器的设置满足旋变数字转换器的10-16 位分辨率的设计要求。

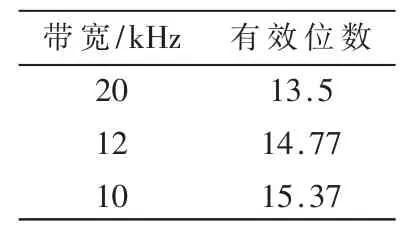
表2 不同带宽下FFT 仿真结果

4 结论

本文设计了一种面向10-16 位旋变数字转换器的Σ-Δ 调制器电路，包括积分器、斩波电路、时钟电路与比较器。利用了Cadence 仿真软件中的Spectre 仿真工具完成了电路的仿真，并利用MATLAB 建模分析了调制器的FFT 波形以验证调制器的性能。根据仿真结果得到，该调制器的设计符合精度要求。