基于离散元素法的薄壁轴法兰磨削阻尼器设计
2022-04-19张兵曹新城孙浩姚斌唐琦王山城
张兵,曹新城,孙浩,姚斌 ,唐琦,王山城
1厦门大学;2中国航发哈尔滨东安发动机有限公司
1 引言
高强度、韧性好的薄壁零件广泛应用在航空航天领域,但其多为结构复杂的难加工材料,加工中的力学表征为动态特性时变,局部刚度差,阻尼小,极易产生振动,对零件的加工精度和加工效率产生负面影响[1,2]。作为动力分流传输的关键零件,薄壁传动轴采用膜片联轴器-法兰一体化结构,端面法兰在磨削过程中的动态特性引起振动响应,造成持续的周期性磨削力作用,静态下测量成品的端面跳动大,且平面度及表面微观形貌难以满足设计要求。
切削振动是影响薄壁零件加工质量和切削效率的关键技术难题,深入研究其振动机理并提出有效的抑振方法对提高薄壁零件的加工质量和加工效率及促进行业的发展具有重要意义。Xiao J.L.等[3]提出了一种多柔点随动支撑头,有效抑制了大型薄壁零件镜面铣削过程中的振动。Wang S.等[4]提出了一种振动主动控制系统,在薄壁件铣削试验中取得了良好的振动控制效果。文献[5]设计了一种电涡流阻尼器,对薄壁盘振动抑制作用明显。分析发现,目前国内外研究多聚焦于薄壁零件铣削加工过程中的振动抑制,轴类薄壁件磨削加工过程的振动抑制却鲜有研究。针对加工中工件旋转的工况,用附加阻尼的方法抑制薄壁零件磨削振动是一种新的技术尝试,其中,被动阻尼减振技术具有实施简单、效果明显及可靠性高等特点,通常用作工程领域振动抑制;而颗粒阻尼技术(Particle Damping Technology)[6,7]属于被动阻尼减振技术的一种,通过密闭空间填充的细小固体颗粒间的摩擦与冲击,使得受控结构的振动能量以热量形式耗散,从而达到调谐结构自振特性和振动抑制的目的。肖望强等[8,9]研究了颗粒阻尼器对大功率齿轮传动系统传动过程中振动和噪声抑制的影响。段勇等[10]采用模型试验方法对颗粒阻尼技术在直升机旋翼桨叶上的应用进行了探索性研究。B.Sathishkumar等[11]使用颗粒阻尼控制固定镗杆的振动,通过在镗杆上填充各种金属颗粒对旋转零件进行镗孔。
本文利用有限元仿真分析了薄壁轴零件动力学特性,据此设计了一种基于颗粒碰撞阻尼技术的薄壁轴法兰磨削减振专用阻尼器,并建立了离散元模型。通过离散元耗能仿真和振动台试验验证了离散元模型的有效性与阻尼器的可靠性,并得出了最优颗粒参数配置的阻尼器方案。最后将优化后的阻尼器应用于现场磨削试验,有效抑制了薄壁轴精密磨削过程中的振动,振动抑制比达70%以上,说明本文研究工作具有较好的工程应用价值。
2 薄壁轴动力学特性模态分析
如图1所示,以某型号军用直升机传动轴为研究对象,采用花键—膜片联轴器—法兰一体化制造,法兰盘端面厚度3.35mm,轴筒壁厚4.28mm,弹性膜片联轴器最薄部位仅0.35mm,是典型的弱刚性薄壁零件。在磨削法兰盘端面时,为预测薄壁轴零件结构动态特性与加工振动,得到受迫振动响应,对薄壁轴零件进行有限元模态仿真和谐响应分析。
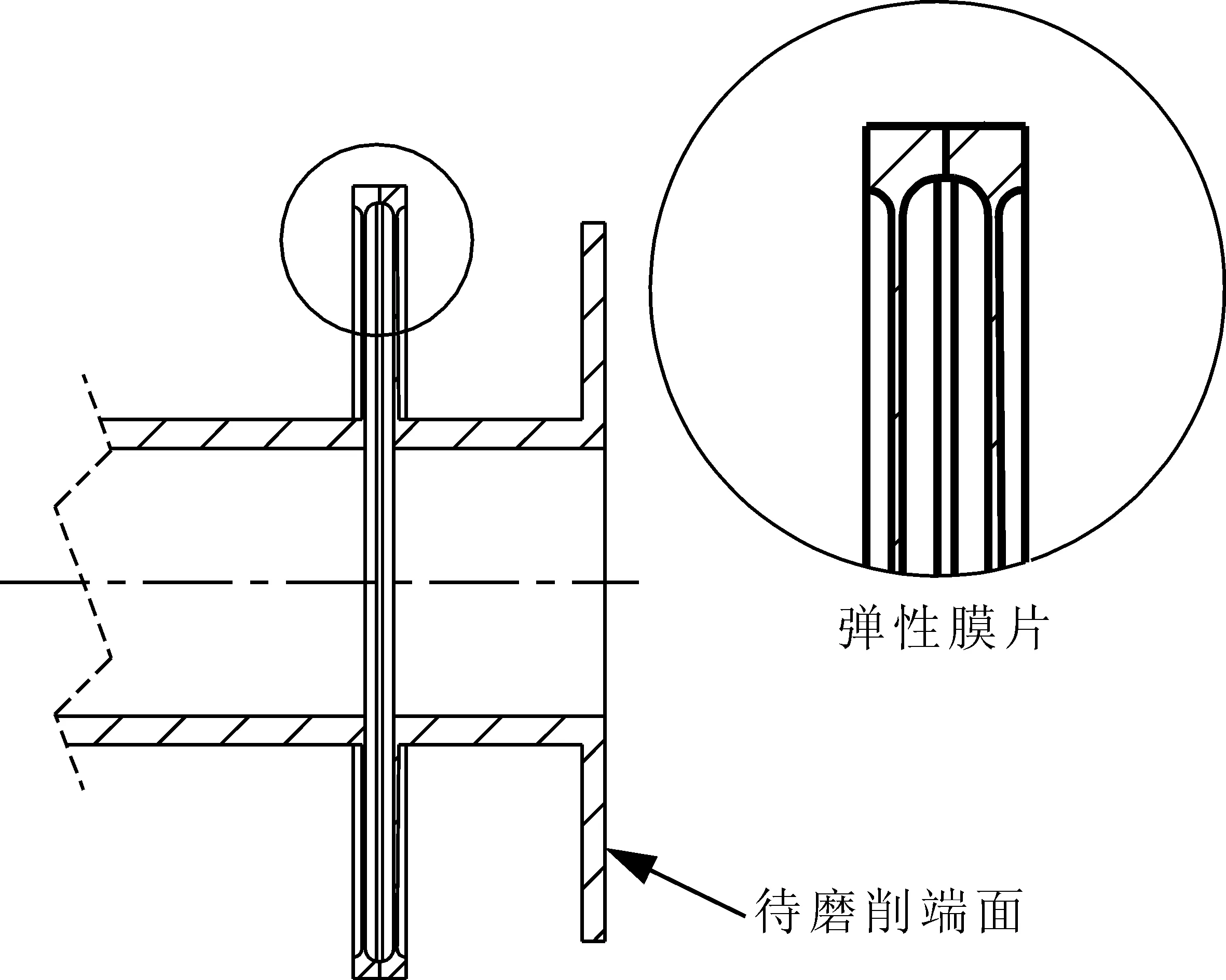
图1 薄壁轴零件结构
依据薄壁轴零件的材料特性设定相应的参数,设定薄壁零件加工时转动角速度为6.28rad/s(主轴转速60r/min),根据现场定位要求限定其他自由度,得到薄壁轴零件前三阶固有频率及对应振型(见表1)。

表1 薄壁轴零件模态振型仿真
从振型图可以看出,薄壁轴零件的膜片联轴器和法兰结构的模态响应明显,振动敏感,为阻尼器结构设计和安装位置的选择提供了参考。
根据上述模态分析得到的模态结果,谐响应分析频率设定为0~300Hz,求解步长设定为30,图2为薄壁轴零件法兰端面某节点的位移—频率响应。简谐激励时,在前三阶固有频率下该节点均出现位移极值,其中,在第三阶固有频率(168.96Hz)下振动响应最大,后续减振设计中应着重抑制该频率下的振动。

图2 薄壁轴零件谐响应结果
3 薄壁轴法兰磨削阻尼器离散元模型
离散元素法是一种有效反映颗粒真实运动的数值模拟方法,能够同时分析颗粒间及颗粒与腔体边界间的相互作用,根据独立碰撞单元间的相互作用(颗粒接触模型)和牛顿运动定律对颗粒运动进行循环迭代计算[12]。颗粒接触模型负责计算单元间的接触力,牛顿第二定律则用于求解碰撞单元位置信息,通过跟踪计算独立单元的微观运动,即可得到研究对象的宏观运动规律。
根据Hertz-Mindlin(no slip)接触理论,本文基于软球模型分析该薄壁轴零件阻尼器离散元模型中的颗粒接触情况。如图3所示,Kn,Ks为碰撞接触单元间法向及切向弹性系数;ηn,ηs为碰撞接触单元间法向及切向阻尼系数;Fn,Fs为碰撞接触单元间的法向力及切向力。
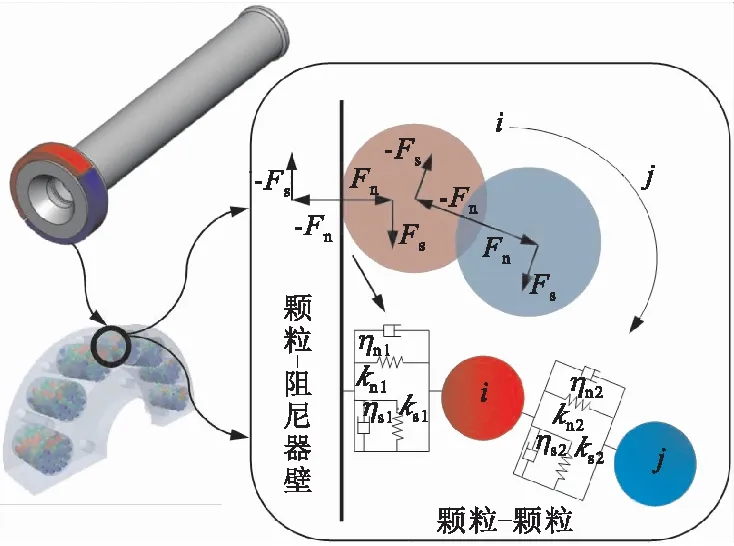
图3 薄壁轴零件颗粒离散元模型
基于软球模型计算循环迭代过程中的单元接触力,其中法向接触力表示为
(1)
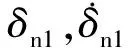
切向接触力表示为
(2)

基于软球模型计算得到了颗粒间的接触力,再根据牛顿第二定律,求得阻尼器中某颗粒在某时刻运动方程[13]为
(3)

4 阻尼器颗粒参数碰撞耗能仿真优化
考虑薄壁轴零件恶劣的磨削环境,选择了耐蚀性能强且成本低的奥氏体-铁素体双相不锈钢(牌号17Cr25Ni7Mo4WCuN)颗粒。参照谐响应分析结果,将薄壁轴零件法兰盘在168.96Hz正弦激励下的振动响应数据作为耗能仿真和后续实验的激励信号。激励信号作用于法兰盘端面,阻尼器对称布置于激励作用点的两侧。对颗粒直径和颗粒填充率进行优化设计,在EDEM软件进行耗能仿真计算,统计单位时间内颗粒碰撞能量损耗。
在统一的颗粒填充率(70%)下,当颗粒直径为1.0mm,1.5mm,2.0mm,2.5mm,3.0mm时,单位时间耗能情况见图5。随着颗粒直径的增加,阻尼器耗能呈现出先增加后减少的趋势,在颗粒直径为2.0mm时,耗能取得最大值。分析认为,同一填充率下,小直径颗粒数量多,阻尼系统间的总碰撞次数多,但单元间的单次碰撞能量损耗较少;大直径颗粒数量少,单元间的单次碰撞能量损耗较多,但阻尼系统的总碰撞次数少。

图4 离散元分析模型
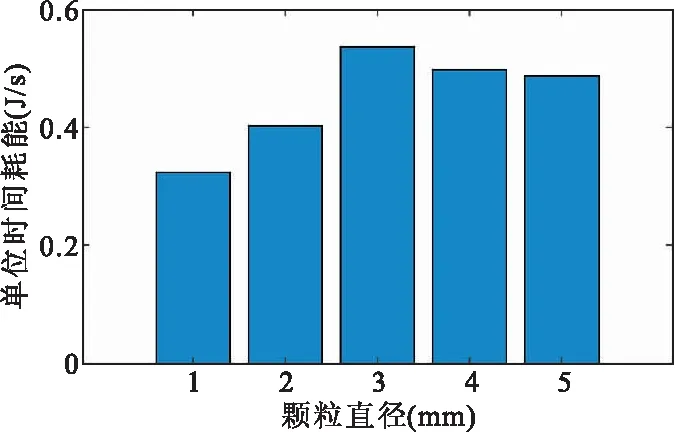
图5 不同颗粒直径的耗能
在统一的颗粒直径(最优粒径2mm)下,对不同颗粒填充率对系统耗能的影响进行仿真分析,统计单位时间内颗粒填充率在30%~90%时颗粒碰撞次数和碰撞能量损耗。如图6所示,随着颗粒填充率的增加,颗粒间碰撞次数和阻尼器耗能均呈现出先增加后减少的趋势,颗粒填充率为70%时,碰撞次数和耗能同时取得最大值。
分析认为,在振动激励和颗粒直径统一的前提下,不同填充率下接触碰撞单元间的单次碰撞能量损耗相同,颗粒间的碰撞总次数越多,则系统总耗能越多。填充率较小时,颗粒数量较少,颗粒间的碰撞总次数较少;填充率较大时,颗粒堆积严重,限制了颗粒间的相对运动,降低了颗粒碰撞总次数。

图6 不同颗粒填充率的耗能与颗粒碰撞次数
综合考虑不同颗粒直径、颗粒填充率方案的系统耗能,可得阻尼器理论最优方案为颗粒直径2mm,颗粒填充率70%。
5 阻尼器抑振效果试验验证
5.1 颗粒阻尼器减振性能模拟试验
为了验证不同激励强度下颗粒阻尼器的鲁棒性,在有无颗粒阻尼器的两种试验条件下采集法兰盘的端面位移数据。阻尼器配置统一选择颗粒直径2mm,颗粒填充率70%。
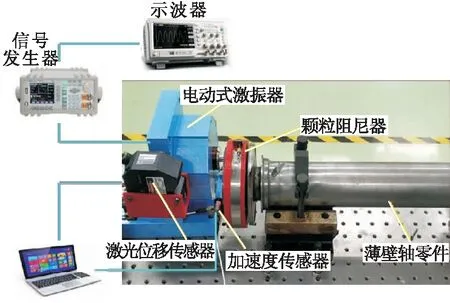
图7 试验装置与测试原理
图8展示了不同激励强度下法兰盘端面跳动幅值。可以看到,在不安装颗粒阻尼器的情况下,端面跳动幅值与激励强度成正比,表明法兰盘自身阻尼极小,可以近似为纯弹性系统。图中深色棒条为安装颗粒阻尼器后法兰盘的跳动状态。可见,安装阻尼器后,法兰盘的跳动烈度存在极限值,随着激励的增强,跳动幅值逐渐放缓,颗粒阻尼器的减振效果越来越显著。
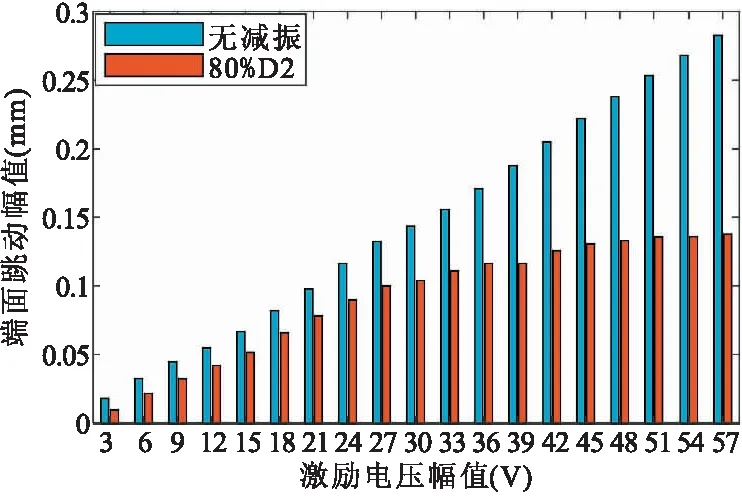
图8 不同激励强度的法兰盘端面跳动幅值
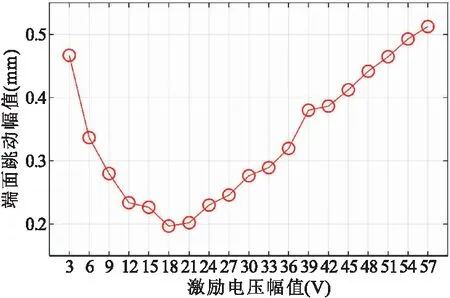
图9 不同激励强度下法兰盘端面跳动幅值下降比率
在不同激励强度下,对比不安装颗粒阻尼器,安装阻尼器后法兰盘端面跳动幅值下降的比率见图9。可见,下降比率随着激励强度的增强先下降后上升,即颗粒阻尼器的减振性能随着法兰盘振动的增强先下降后上升。在法兰盘自由振动的幅值为0.02mm时,下降比率为46%;在法兰盘自由振动的幅值为0.08mm时,下降比率为20%;在法兰盘自由振动的幅值为0.28mm时,下降比率为51%。
5.2 阻尼器颗粒参数优化试验
对不同颗粒直径和不同填充率的阻尼器配置方案进行振动台试验,最终得到薄壁轴零件法兰端面的加速度值,加速度值的大小可直接反应振动的强弱。在不同直径颗粒和不同颗粒填充率下,采用双坐标图的形式展现系统耗能与加速度均方根值(见图10和图11)。

图10 不同颗粒直径时的仿真和试验对比

图11 不同颗粒填充率时的仿真和试验对比
从仿真角度分析,系统总耗能越大,说明阻尼器减振效果越好;从试验角度分析,加速度均方根值越小,说明阻尼器减振效果越好。通过上图对比分析,在阻尼器减振效果的变化趋势方面,仿真结果与试验结果取得了良好的一致性,验证了离散元模型的准确性。在颗粒直径取2mm,颗粒填充率取70%时,阻尼器的减振效果最好。
5.3 现场磨削试验验证
将配置最优颗粒参数(颗粒直径2mm,颗粒填充率70%)的阻尼器安装在薄壁轴零件上进行现场磨削试验(见图12)。主轴转速为60r/min,砂轮转速1389r/min,砂轮进给速度0.015mm/min,进给余量0.04mm。

图12 磨削减振试验
受主轴旋转工况的限制,采用激光位移传感器采集法兰盘端面振动数据。分别采集有无阻尼器磨削的法兰盘端面跳动数据,图13为位移时域数据的对比。无阻尼器磨削法兰盘端面位移幅值为0.025mm,有阻尼器磨削法兰盘端面位移值降至0.015mm,下降比率达40%。

(a)无阻尼器位移时域数据

(b)安装阻尼器位移时域数据
图14为有无阻尼器磨削时位移的频谱对比。由图可得,无阻尼器磨削频谱图后两个高峰为薄壁轴零件的共振区,对应薄壁轴零件的二、三阶固有频率;有阻尼器磨削频谱图一阶峰值几乎稳定不变,二、三阶峰值显著降低,振动明显被抑制,振动抑制比分别为71.9%,76.9%。
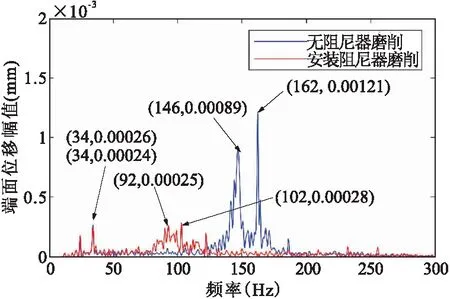
图14 位移频谱对比
6 结语
(1)建立薄壁轴零件有限元模型对振动进行分析,通过模态分析得到了各阶固有频率和振型,膜片联轴器和法兰对振动的响应比较敏感;通过谐响应分析得到了法兰端面节点的位移-频率响应,在第二、三阶固有频率下的位移响应较大。
(2)基于离散元法建立了薄壁轴零件的离散元模型,通过仿真计算和振动台试验分析了不同颗粒参数(颗粒直径、颗粒填充率)对阻尼器耗能效果的影响规律,证明了离散元模型的可靠性和仿真结果的有效性,得出了最优颗粒参数为颗粒直径2mm,颗粒填充率70%。
(3)将配置最优颗粒参数(颗粒直径2mm,颗粒填充率70%)的阻尼器安装在薄壁轴零件上进行现场磨削试验,薄壁轴零件在第二、三阶固有频率下的振动响应得到明显抑制,振动抑制比达到70%以上。
(4)在不改变加工工艺和零件结构的前提下,用附加阻尼的方法实现薄壁零件磨削振动抑制是一种新的尝试,为颗粒碰撞阻尼技术在薄壁零件磨削振动抑制领域的推广提供了工程应用范例。
