基于并行模拟退火的多目标航空器着陆问题的TOPSIS 分析

李春霖 王赫 牛海晴 乔栎霏 赵嘉晨 杨群亭

（中国民航大学，空中 交通管理学院，天津 300300）

由于航空器在终端区着陆的排序机制和管制员的服务顺序以及航班量的增加等问题，航班延误的现象愈加频繁。飞机着陆排队问题（ALP）便是导致延误现象的主要影响因素之一。由于机场跑道容量的有限性，当有大量航班同时降落于同一机场时，部分航班便不能在他们首选的降落时间（PLT）降落，因此造成了延误。

本文主要研究如何通过合理的航班排序来减小延误时长，提高综合保障能力。我们设计了一个多目标飞机着陆问题（MOALP）模型，将MOALP 分解为两个子问题：飞机排序问题和最优着陆时间搜索问题。因此造成了可行解数量庞大的问题，为此我们使用了并行计算来减少计算时间。

此外，为了帮助决策者从有限的备选方案中选择最优方案，我们采用了TOPSIS 赋值方法，将TOPSIS 算法伴随PSA(TOPSIS&PSA)应用于飞机着陆问题的工作。这种技术基于的原则是，所选的替代方案与正理想的距离最小，与负理想的距离最大。TOPSIS 被广泛用于处理现实世界中的多标准决策问题，在我们的工作中，我们通过最小化最大延迟和预定着陆时间和首选着陆时间之间的方差来表达公平性。

目前的大多数研究都将ALP 制定为多个目标：最小化总延迟、最大化跑道容量等。研究了飞机在单条跑道上着陆的动态多目标调度方法，但大部分仅给出了一组权重，而在实际中，不同的利益相关者可能会给出不同的权重。在中国民航发展快速的今天，空管- 航班的综合优化成为减少延误的重要措施。

本文主要成果可以总结如下：（1）首次将TOPSIS 应用于探索多目标飞机着陆问题的满意解决方案, 以相对较低的成本解决了多目标的问题。（2）我们提出了一种单机多线程并行SA 算法来加快多目标飞机着陆问题的解决。

1 模拟退火方法

为了避免产生局部最优解，我们采用了模拟退火（SA）方法，接受较差的解。模拟退火算法是使局部最优解能概率性地跳出并最终趋于全局最优的方法。SA 在达到最优结果时终止，完成预定的迭代次数被认为是自适应大邻域搜索的停止准则。

2 算法模拟步骤

通过最小化飞机之间延迟的差异来最大化公平性

公式（6）是根据MOLAP 模型对不同的类别设置不同参数以确保亏损最小化。条件（8-9）保证了着陆次序。条件(10) 确保所有航班都被安排着陆。条件（11）意味着不同航班的着陆时间必须满足最小着陆间隔时间（MST）。

3 参数设置与初始化模式

初始优化序列为A0，初始优化调度时间为X0。

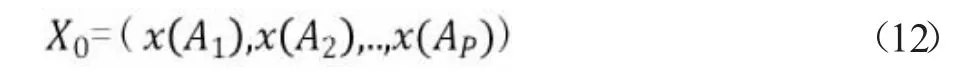
wk的值以表1 呈现。表1 中每一行代表了不同目标状态的重要性（相对重要性）。每一组不同的权重代表不同的利益相关者。

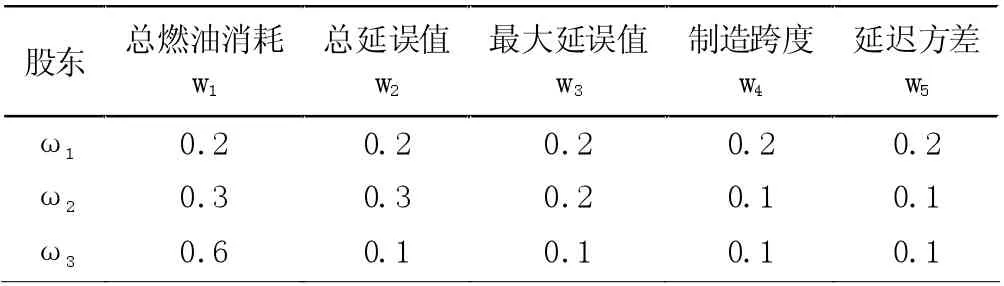
表1 面向多股东的不同利益权重矩阵

4 模型构建

4.1 先来先模式算法（FCFS）

在FCFS 的服务规则和算法中，每架飞机都有一个不受约束的时间。

假设有P 架次航班（a1，a2，…，ap），它们的最佳着陆时间（PLT）为Ti。每一架次航班ai的属性包含（航班号，最早到达时间，计划到达时间，最新到达时间, 航空器类别）。假设由PLT 自动生成的着陆次序为A0。Ai-1及Ai之间的安全间隔为SAi-1，Ai。每个航班的预定着陆时间（SLT），x（Ai）计算公式如下所示。

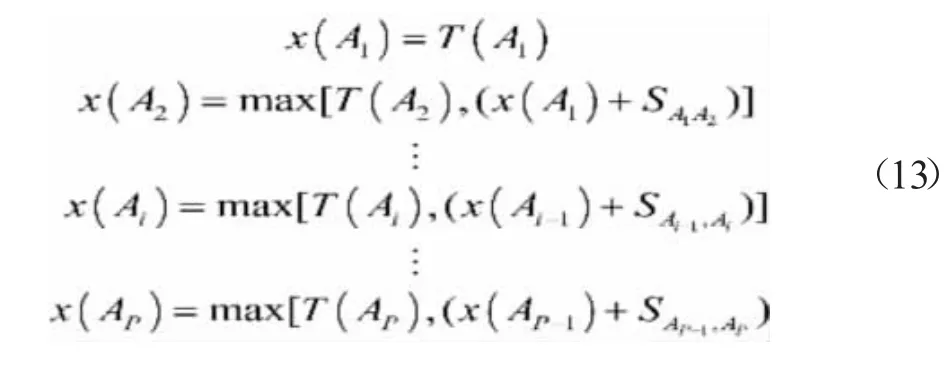
4.2 单线程模拟退火算法（SA）

4.2.1 序列更新模式

单线程SA 算法中的序列更新采用双交换法和三交换法以相同的概率更新飞行着陆序列，见图1。

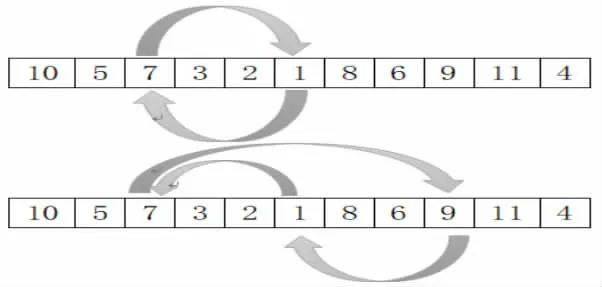
图1 二交换法（上）、三交换法（下）

4.2.2 局部贪婪搜索算法

确定序列时，只使用最早的到达时间。初始SLT 的计算公式如下。

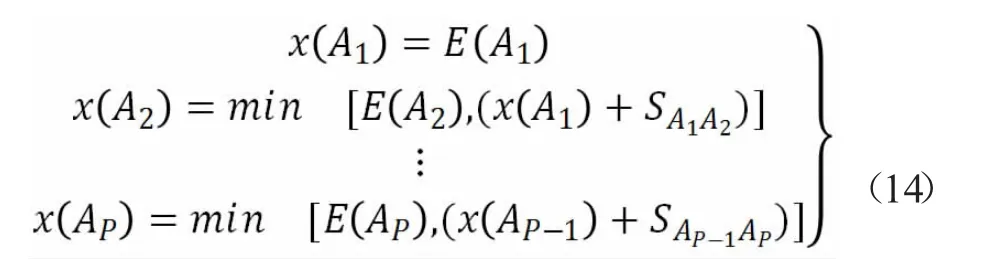
4.3 并行模拟退火算法（PSA）

PSA 的目的是将表1 中加权值对应的SA 计算分配给工人进行并行退火计算。PSA 如图2 所示。

图2 并行SA 算法

5 TOPSIS 评估方法

步骤1：根据决策矩阵计算归一化的决策值矩阵，用以下公式计算：

wij是第i 个利益相关者确定的的第j 个目标值的权重。

步骤3：从加权归一化决策值矩阵中确定正理想解和负理想解。由于这五个属性都是基于成本的，所以正

第6 步：按降序排序，得到TOPSIS 结果。Ci的值越低，对应的解更接近理想解。

6 结论

通过上文利用天津机场的实际数据，得到了FCFS、常规SA 和PSA 的测试结果，见表2。

表2 比较计算时间

通过与常规SA 和FCFS 的比较，证明了基于PSA(TOPSIS&PSA) 的扩展TOPSIS 的有效性。MATLAB 分析器对FCFS 报告的计算时间为0.389 秒。结合常规SA 的着陆顺序和调度着陆时间和常规SA 的五种成本由MATLAB 分析器进行的常规SA 报告的计算时间为135秒。对PSA 的结果进行TOPSIS 评价，将不同的权重集来进行效率比较。可以得出PSA(TOPSIS&PSA)报告结果的TOPSIS 评估计算时间为99 秒。

通过表3 可以发现FCFS 的计算时间是最短的，但是这五个成本大于其他两种方法。与其他两种方法相比，常规的SA 消耗更多的计算时间，但其五个成本低于FCFS。TOPSIS&PSA 的计算时间比常规的SA 的计算时间低，而且其四种成本都低于常规的SA。常规SA 的计算速度可能太慢，导致ATC 响应时间的显著减少。

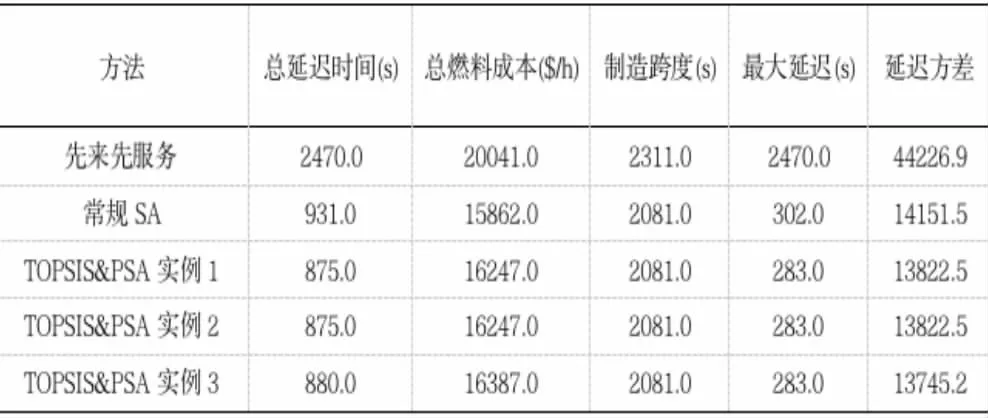
表3 比较三种方法的五种成本

而后我们对各个方法的结果敏感性进行分析。首先通过改变权重来进行研究，观察评估结果是如何随着权重的改变进行反馈的。其次从理论上详细推导出使评估结果不变的变化范围，并对三种方法进行比较和讨论，计算时间和五种方法的对应成本，见图3。

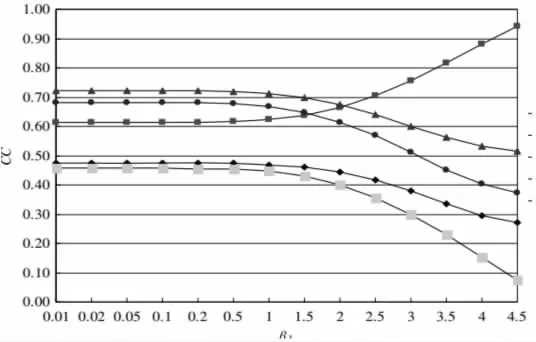
图3 不同单一变异比条件下的闭合系数

通过对比我们发现这五个成本将随着权重集数量的增加而降低，这意味着我们可以通过增加权重集数量来提高获得更理想解的概率。所以理论上，TOPSIS&PSA比常规SA 更理想和有效，在不同的权重集下，得到理想解的概率至少是常规SA 的几倍。

本文提出了一种基于PSA 的飞机着陆问题多目标优化TOPSIS 评价方法，用于飞机着陆问题的多目标优化和不同股东利益的权衡。通过对比实验结果发现，当采用常规SA 方法求解着陆问题时，各目标的权重对多目标优化结果有很大影响。此外，即使已经设置了适当的参数设置，如果只运行一次常规SA，就很难得到最优解，TOPSIS 和PSA 比常规SA 更容易获得理想的解决方案。尽管利益方给出的权重并不准确，但仍然可以以相对较低的成本找到令人满意的解决方案。在未来，我们将探索一种更有效的模拟退火算法来代替贪婪算法以减少计算时间。此外，通过多计算机分布式并行计算，增加可用线程的数量和权重集，以实现最优解，还需进一步的研究。