真空断路器动态特性仿真与最优化设计
2022-04-19仲丽晓
李 斌,仲丽晓,姜 岩
(1.辽宁工程技术大学电气与控制工程学院,葫芦岛 125105;2.国网辽宁省电力有限公司营口供电公司,营口 115002)
在电力系统的继电保护装置中,断路器是较为重要的开关器件[1]。断路器发生故障引起的后果相对比较严重,尤其是在高电压等级的电力系统中,当断路器出现异常时,首先影响断路器保护范围内输电线路和电力设备,其次还会引发电网事故[2-3]。对断路器进行优化设计能够提升断路器的性能,减轻电弧对断路器的烧蚀,延长断路器的使用寿命,研究断路器的动态特性能够一定程度上防止断路器出现故障。
本文利用近年来兴起的虚拟样机技术对断路器进行了动态特性研究和优化设计。虚拟样机技术是在研发产品过程中,运用元器件的三维模型和模型的动态特性分析技术,再通过现代计算机技术搭建出整个产品的三维立体模型,最终虚拟样机技术能够仿真产品实际运行情况,得到一系列的实验数据,利用计算机对这些数据进行分析[4]。对产品的性能做出评估、预测,同时也可以对模型进行改进,达到优化产品的效果。
将虚拟样机技术运用于断路器设计具有以下优势:
(1)能够对产品外观三维模型和其内部机械构造进行设计。利用虚拟样机技术可随时对断路器的多种参数进行修改,此外虚拟样机软件一般带有优化设计模块,可以对断路器进行优化。最后确定断路器的设计方案,能够直接对产品模型进行仿真,观察实验结果,根据实验结果决定是否修改实物模型的参数,这样大幅缩短了断路器的研发周期。
(2)虚拟样机技术能够实现断路器的实时装配与动态仿真。传统断路器装配产品时往往会出现产品元件之间的不兼容,产品在运行中会出现错误。虚拟样机技术能够在一定程度上提前预知断路器元件之间的不兼容性和可能会出现的错误,这样就能在断路器的研发过程中避免不必要的材料浪费。
(3)可对断路器进行运动学与动力学分析。机械系统动力学自动分析软件ADAMS(autonatic dynamic cnalysis of mechanicd system)可仿真产品的实际应用状态。对断路器进行参数优化时,不用制造真实的物理样机就能提前评估产品的综合性能[5-6]。由于人机交互界面友好,所以能够方便快捷地观察产品在多种情况下的性能,为产品的优化设计提供参考。
1 永磁真空断路器虚拟样机模型
1.1 12 kV 真空断路器实物模型
本文真空断路器的虚拟样机模型是依据实际的LGD-12 型高压永磁真空断路器建立的,其额定电压为12 kV,额定电流为630 A,额定短路分断电流为20 kA。图1 为LGD-12 型真空断路器结构,可以看出断路器配备组合隔离开关,为断路器检修人员提供明晰的可视断口,保证生命财产安全。此外该断路器采用新型绝缘结构,将真空灭弧室、主导电回路、绝缘支持机构高效地集成在一个极柱中,有效减小了断路器的体积,符合断路器向小型化发展的趋势。断路器的基本参数见表1。
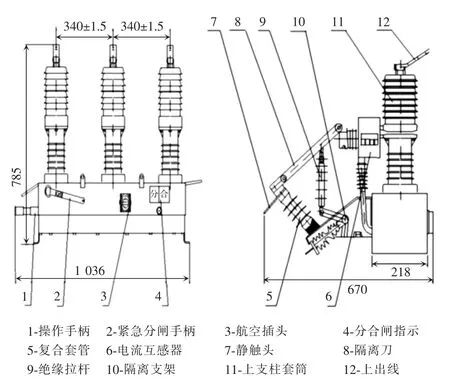
图1 LGD-12 型真空断路器结构Fig.1 Structure of LGD-12 vacuum circuit breaker

表1 真空断路器基本参数Tab.1 Basic parameters of vacuum circuit breaker
真空断路器动力来源是单稳态永磁操动机构,如图2 所示,永磁机构连接形式如图3 所示。进行合闸操作时对励磁线圈通电流,该电流产生的磁场与永磁体产生的磁场同向,动铁心在磁场的作用下移动,同时带动传动杆[7-13]。分闸操作仅需对励磁线圈通以相反的电流,产生的磁场如图2 中所示,在磁场和分闸弹簧的作用下动铁心带动传动杆移动,再通过机械结构使动触头动作,从而完成断路器的分合闸操作。

图2 单稳态永磁操作机构Fig.2 Monostable permanent magnet operating mechanism

图3 永磁机构连接形式Fig.3 Connection form of permanent magnetic mechanism
1.2 断路器数学模型
永磁真空断路器中多个机构相互影响共同决定着断路器分、合闸过程中的动态特性,包括由线圈和单稳态永磁体构成的电磁操动机构、将永磁机构产生的力转换为供断路器动触头动能的机械传动机构。这些机构的正常运行涉及多个物理学过程,包括永磁体线圈将电场能转化为磁场能,产生的磁场又与永磁体的磁场相互耦合和分闸弹簧支配着动铁心的运动,其中机械结构的运动又涉及物体动力学。电容器为断路器供电,将电容器的两端接在永磁体的线圈上,再配合分闸弹簧可以实现断路器的分合闸操作。根据上述描述可以建立麦克斯韦方程为

式中:ψ 为整个电磁系统的磁链;UC为电容器C 两端的电压;i 为线圈电流;m 为移动模块的等效质量;x 为动铁心位移;v 为动铁心的运动速度;Fx为电磁机构产生的电磁力;Ff为运动负载反力;δ 为动铁心和静铁心之间的空气间隔。
图4 为真空断路器传动杆与曲轴臂结构,曲轴臂连接传动杆和动触头部分。因为永磁机构带动动铁心只能在x 轴方向移动,而曲轴臂将传动杆x 轴方向的力转换为动触头所需的y 轴方向的力[9-14]。

图4 真空断路器传动杆与曲轴臂结构Fig.4 Structure of transmission rod and crankshaft arm in vacuum circuit breaker
传动杆和动触头的运动关系为

式中:vA和SA分别为传动杆的水平速度和位移;vB和SB分别为动触头的垂直速度和位移;α 为传动杆和曲轴臂之间的夹角;x0为当断路器处于分闸或合闸位置时曲轴臂末端在x 轴上距原点O 的距离;y0为当断路器处于分闸或合闸位置时曲轴臂末端在y轴上距原点O 的距离。如果位移矢量指向x 轴或y轴正方向,那么位移为正值,否则为负值。
1.3 12 kV 真空断路器虚拟样机模型
为了研究断路器的动态特性,在ADAMS 软件建模的过程中简化了模型,以突出各部件数学上的关系,没有搭建实物中的隔离开关、航空插头等不重要的辅助装置,保留了断路器的躯干装置[15-16]如图3 所示。为了保证仿真的准确性,施加在各个元件的约束是根据真实情况所添加的。所建立的虚拟样机模型如图5 和图6 所示。图5 中连接弹簧为缓冲装置,可以吸收过大的分闸力,减小分闸反弹幅值。传动柄与地之间添加的是水平滑动副,所以传动柄只能沿着x 轴方向运动;在动触头上添加了垂直运动副,来确保动触头只能在垂直方向上运动;在动触头和绝缘连杆之间添加了固定副,以此来确保动触头被固定在绝缘连杆上;在传动柄和曲轴臂之间添加了旋转副,在曲轴臂和绝缘连杆之间也添加了旋转副,来确保它们之间正常的转动。根据实际情况下所有的运动副之间都考虑了摩擦力的影响,采用库伦摩擦模型,摩擦系数设置为μs=μd=0.05[17-19]来计算操动机构之间的摩擦力,其中:μs为静摩擦力系数,μd为动摩擦力系数。

图5 LGD-12 真空断路器仿真模型Fig.5 Simulation model of LGD-12 vacuum circuit breaker

图6 LGD-12 真空断路器三视图Fig.6 Three views of LGD-12 vacuum circuit breaker
1.4 实验与仿真数据对比
实验利用LGD-12 型配永磁机构真空断路器及其配套使用的控制器,如图7 所示。其额定电压12 kV、额定电流630 A、额定短路分断电流为20 kA。实验数据主要采集断路器动触头的位移曲线,实验电路由微处理器和位移传感器等构成,其控制系统组成如图8 所示。本文采用FXB-V 系列DC±12~±18 V、0~20 mm LVDT 线性位移传感器。位移传感器能够将动触头的位移转换为电信号,数字信号微处理器能够采集、处理位移传感器所收集到的电信号,最终得到断路器的位移特性。

图7 真空断路器与智能控制器实物Fig.7 Entities of vacuum circuit breaker and intelligent controller

图8 断路器控制系统组成Fig.8 Composition of circuit breaker control system
合闸过程中触头行程曲线如图9 所示,可以看出断路器虚拟样机有摩擦力的仿真数据与实验数据吻合较好,仿真曲线略快于实验曲线,这是因为虽然考虑了断路器操动器件之间摩擦,但仿真数据仍是理想的条件下,致使两组数据有略微出入,但误差属于可以接受的范围内。

图9 合闸过程中触头行程曲线Fig.9 Contact stroke curves in the closing process
图9 中,无摩擦力的仿真曲线与其他两组曲线相比,较快地完成了合闸,但合闸后的振动幅度较大,而合闸过程中无摩擦力的实验数据与实际偏差较大,所以最终模型为无摩擦力的虚拟样机模型。从图9 的实验曲线可以看出,在合闸过程中刚开始合闸时动触头出现一定程度的抖动,这是因为操作机构有一定的反作用力。永磁机构提供的力超过反作用力,使得动触头向上运动。合闸过程在53.3 ms完成,接着触头有5 ms 左右的抖动,在合闸过程的末尾动触头因永磁机构的磁力保持在合闸位置。
分闸过程中触头行程曲线如图10 所示,可以看出考虑摩擦的仿真曲线与实验曲线吻合较好。与合闸过程一样,考虑摩擦力的曲线略快于实验曲线。未考虑摩擦力的分闸仿真也存在着过早完成合闸、触头反弹幅度较大、反弹过程持续时间较长的问题。从图10 中有摩擦力的曲线可以看出,触头在37.5 ms 发生移动,且有较大的初速度,分闸弹跳发生在44 ms,振幅为1.86 mm,之所以产生弹跳是因为传动柄的缓冲结构和分闸弹簧造成的。
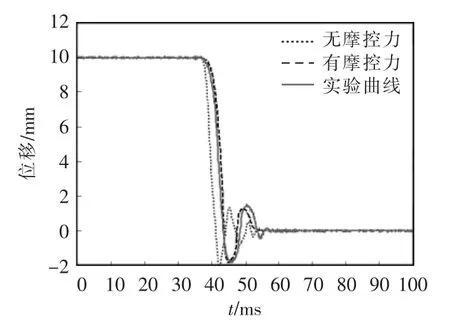
图10 分闸过程中触头行程曲线Fig.10 Contact stroke curves in the opening process
实验与仿真数据对比见表2,可以看出考虑摩擦力的断路器虚拟样机模型能够很好地模拟实际分合闸过程中动触头的运动情况,这验证了虚拟样机模型搭建的正确性。

表2 实验数据与仿真数据的对比Tab.2 Comparison between experimental and simulation data
1.5 断路器的动态仿真结果分析
从第1.4 节可看出仿真数据与实验数据吻合较好,说明了搭建的虚拟样机模型符合实际的断路器模型,因此可以对仿真结果进行深入分析。
动触头合闸特性曲线如图11 所示,可看出动触头在20 ms 时开始运动,52.1 ms 时首次与静触头相接触,53.6 ms 时发生弹跳,55.2 ms 时达到反弹峰值0.061 mm。由触头的速度曲线可以看出,50.5 ms 时触头达到最大正向速度1.142 m/s,54.4 ms 时达到了反向最大速度0.275 m/s,58.8 ms 时速度为0,停止运动。
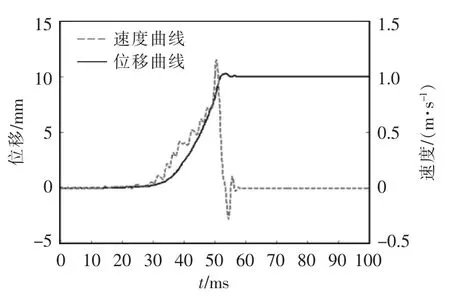
图11 动触头合闸特性曲线Fig.11 Closing characteristics curves of moving contact
动触头分闸特性曲线如图12 所示,可看出动触头在37.5 ms 开始运动,45 s 时分闸弹跳发生,50 ms 时动触头弹跳达到峰值,振幅为1.24 mm,振动历时约10 ms,整个分闸过程历经54 ms;43 ms 时动触头达到最大速度4.3 m/s,此时触头开始反弹,在47 ms 时动触头达到反弹的最大速度2.1 m/s。

图12 动触头分闸特性曲线Fig.12 Opening characteristics curves of moving contact
2 真空断路器虚拟样机模型的优化设计
2.1 影响断路器分闸弹跳因素
在分闸过程中,当触头到达分闸结束位置时,由于受到操作机构和缓冲弹簧的影响,触头发生振幅衰减的阻尼振动。与合闸弹跳过程相比,分闸弹跳更明显,但随着断路器的发展,断路器的开距越来越小,过大的分闸弹跳会引起二次电离,从而发生电弧重燃的现象。因此,断路器分闸弹跳的研究对断路器的性能和电力系统的可靠性有着重要意义。
影响分闸弹跳的3 种因素有:动触头缓冲弹簧的刚度系数、分闸弹簧的预压力和曲轴臂的质量。通过设定断路器虚拟样机的3 种影响因素的数值来比较在不同情况下分闸弹跳的幅度和分闸过程所用的时间。
1)缓冲弹簧的刚度系数对分闸弹跳的影响
不同刚度系数的动触头位移曲线如图13 所示。当缓冲弹簧的刚度系数从100 N/mm 增加到250 N/mm,开闸弹跳幅度从2.81 mm 降到1.82 mm。这说明随着缓冲弹簧的刚度系数增大,会抑制动触头在分闸过程中弹跳的幅度。虽然缓冲弹簧的刚度系数不同,但分闸过程所用的时间几乎相同,这说明缓冲弹簧的刚度系数对分闸过程所用时间的影响较小。

图13 不同刚度系数情况下动触头位移曲线Fig.13 Displacement curves of moving contact with different stiffness coefficients
本设计的仿真对象是一个单稳态永磁操作机构。动触头之所以能够保持在分闸位置是因为有分闸弹簧的拉力存在。在断路器的分闸过程中,传动柄将会与缓冲弹簧碰撞,当触头到达分闸位置时,传动柄将会发生反弹,然后由曲轴臂将绝缘拉杆和传动柄连接起来,于是在传动柄的带动下,绝缘拉杆也会在垂直方向上弹跳,最终导致动触头的上下弹跳。当触头发生弹跳时缓冲弹簧会吸收移动元件的动能,而缓冲弹簧的弹性势能为

式中:Ek为弹簧的弹性势能;k 为弹簧的刚度系数;x1为弹簧的形变量。
根据式(5),在相同形变量下,更大的缓冲弹簧刚度系数会使缓冲弹簧拥有更大的弹性势能,即更大的刚度系数会使弹簧从运动元件中吸收更多动能,缓冲器有更好的缓冲效果,动触头有更小的弹跳振幅。
2)分闸弹簧预压力对分闸弹跳的影响
分闸过程中,不同分闸弹簧预压力下动触头位移曲线如图14 所示。当触头弹簧预压力从750 N增加到3 000 N 的过程中,断路器动触头的分闸弹跳幅度从1.77 mm 增长到2.71 mm。图14 的行程曲线揭示了触头弹簧的预载荷会增大分闸的速度,同时也使触头分闸弹跳的幅度增大;另外,不同分闸弹簧预压力的情况下,分闸过程所用时间也几乎相同,与图13 的分析一致,说明分闸弹簧的预压力对分闸过程所用的时间影响较小。

图14 不同分闸弹簧预压力情况下动触头位移曲线Fig.14 Displacement curves of moving contact with different preloads of opening spring
弹簧的预载荷可等效为弹簧预先储备的弹性势能,当执行分闸指令时,弹簧的弹性势能转换为器件的动能。因此动触头将会获得更大的初速度,加速合闸操作,使传动柄与缓冲器碰撞时有更大的速度,产生更大的冲击。根据能量守恒,该过程的能量守恒方程为

式中:m1为传动柄的质量;v0和v1分别为分闸过程中触头与缓冲器碰撞前、后的速度;e 为缓冲器的恢复系数。在传动柄的质量和缓冲器恢复系数不变的情况下,更大的触头弹簧预压力可以使传动柄获得更大的碰撞初速度v0。但这也会导致动触头分闸弹跳幅度增大。
(3)曲轴臂的质量对分闸弹跳的影响
不同曲轴臂质量的动触头位移曲线如图15 所示。当曲轴臂的质量从2.5 kg 增长到10 kg 时,断路器的动触头弹跳幅度从1.8 mm 增加到2.63 mm,并且分闸时间从55 ms 增加到60 ms。曲轴臂质量增大,惯性增大,所以响应速度变慢,同时弹跳幅度增大。动触头的分闸行程曲线说明更大的曲轴臂质量会延迟分闸的时间,同时也会增大动触头的分闸弹跳幅度。曲轴臂质量为2.5 kg 时分闸过程所需的时间最短,为55 ms。曲轴臂的质量越轻,意味着其惯性就越小。在相同的弹簧拉力情况下,质量越轻的曲轴臂在一定时间内将会获得更大速度,因此质量更轻的曲轴臂能使动触头更快地完成分闸操作。

图15 不同曲轴臂质量情况下动触头位移曲线Fig.15 Displacement curves of moving contact with different mass of crankshaft arm
2.2 综合最优化设计
为了达到最终优化的目的,考虑上述3 个影响分闸性能的关键变量进行虚拟样机实验。因为每个变量都有4 个不同值,共有4×4×4=64 个不同组合,为了求得最优解,共进行了64 次实验。并用触头运动时间tm和触头反弹幅度lb对64 次实验进行评价。从图13~图15 可以看出从触头开始运动到最终静止,最长不超过30 ms,触头最大反弹量不超过3 mm。由此可列出评价原则为

式中:tm为每次实验触头运动时间;lb为每次实验触头反弹幅度;分别为触头运动时间和触头反弹量在评价中所占的权重。因为触头运动时间和触头反弹量都比较重要,所以设=0.5。用式(7)和式(8)对64 次实验进行打分,得分最小者即为

对应的触头弹簧的刚度系数、触头弹簧预压力、曲轴臂的质量即为最优解。
64 次实验中的最优解为:触头弹簧的刚度系数为250 N/mm,分闸弹簧预压力为1 500 N,曲轴臂的质量为5.0 kg。优化前后动触头位移曲线如图16 所示,可看出优化模型将分闸结束时间从54.7 ms 降到48.5 ms,时间缩短了11.33%,即6.2 ms。将触头的弹跳幅度从1.254 mm 降低到1.002 mm,降幅达20.1%,即0.252 mm。

图16 优化前后动触头位移曲线Fig.16 Displacement curves of moving contact before and after optimization
3 结论
用ADAMS 软件建立了LGD-12 型高压永磁真空断路器的虚拟样机模型,并验证了虚拟样机模型的正确性。为了减小断路器弹跳的振幅和弹跳时长,对断路器的虚拟样机模型进行优化设计,得到下列结论:
(1)缓冲弹簧刚度系数的增加可以限制触头分闸弹跳的振幅。
(2)增加触头的预载荷可以加速分闸的过程,但也会使触头分闸弹跳的振幅增大。
(3)增加曲轴臂的质量会降低分闸速度,增大触头分闸弹跳的振幅。
(4)进行了64 次虚拟样机实验,并提出了实验性能的评价标准。根据评价标准,列出了64 次实验结果中的最优解,优化后的模型性能有较大幅度的提升。
