基于模型预测控制单电感双输出Buck变换器的仿真分析

贺素霞，张具琴

（黄河科技学院工学部，河南 郑州 450063）

0 引言

传统的Buck变换器结构简单、易控制，在光伏发电系统中得以大量应用[1]。单电感多输出（Single-Inductor Multiple-Output，SIMO）DC-DC变换器在Buck变换器基础上拓展而来，可实现多路独立输出，具有体积小、效率高和损耗低等优点，近年来在各种应用场景中引起了广泛的关注[2]。与单输出Buck变换器相比，单电感双输出（SIDO）Buck变换器增加了两个开关管，其建模更加复杂[2]，与之匹配的控制器设计以及求解伏-秒平衡方程也更加困难。

尽管经典控制策略设计SIDO变换器控制环路的理论计算和实践过程十分复杂，且在多输出的情况下应用受限，但与高级控制策略，如自适应控制、分数阶控制、模型预测控制（MPC）和H∞相比，仍具有易于校准的优势。

文献[3]对电力电子和传动中采用的无差拍控制、MPC、轨迹控制和滞后控制等不同的预测控制技术进行了详细地阐述，并与PID控制进行了比较。文献[4]，[5]将高级控制应用在多输出功率变换器中，与经典控制相比，减少了输出之间的交叉影响，提高了变换器的暂态性能。高级控制方法通常是根据要求来优化用户定义的代价函数。文献[6]归纳了MPC的设计步骤。文献[7]通过引入Kalman滤波器对电感电流和占空比施加约束，有效地抑制了由输入干扰引起的输出波动，实现了同步Buck变换器的最优控制。文献[8]，[9]详细分析了基于增广状态空间矩阵的模型预测控制的设计以及开关变换器预测控制的实现。

MPC拥有比经典控制更好的轨迹跟踪性能，同时，它引入了一个非线性约束，使得多变量系统具有快速响应的性能，常应用于PI补偿的同步Buck变换器[10]。本文将MPC引入SIDO Buck变换器中，并改进了相应的控制算法。首先使用状态空间平均法建立SIDO Buck变换器的状态空间矩阵，推导出相应的传递函数；然后基于目标模型所建立的状态空间平均模型推导出输出预测，根据模型和性能要求选择合适的代价函数，求解得出最优控制信号；最后使用MATLAB软件进行仿真，并与PI控制进行了对比。

1 SIDO Buck变换器

1.1 基本工作原理

SIDO Buck变换器的拓扑结构和稳态工作时序如图1所示。图中：V1和V2为变换器两路输出电压；IL为变换器的电感电流。详细的系统设计参数如表1所示。

图1 SIDO Buck变换器拓扑及开关时序Fig.1 Topology and switching timing of SIDO Buck converter

表1 SIDO Buck变换器的设计参数Table 1 Design parameters of SIDO Buck converter

变换器通过调整D1和D2控制输出电压的大小；通过控制开关管S1，S2和S3调节输入功率的大小和输出功率的流动方向，其中S3和S1为互补的门极脉冲信号。

在理想情况下，利用伏—秒平衡方程获得变换器的直流稳态增益为

当0

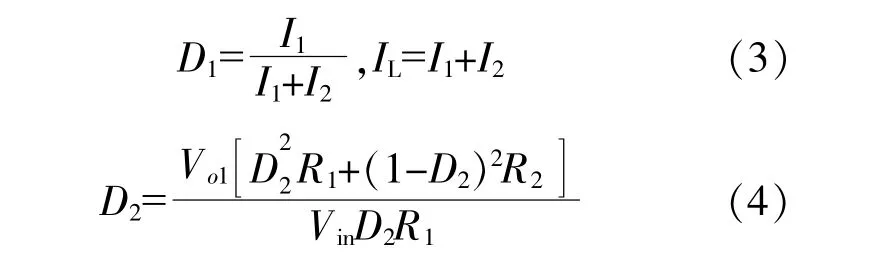
1.2 SIDO Buck变换器的传递函数

图1所示的SIDO Buck变换器的开环传递函数矩阵为[2]

由式（5）可知，传递函数矩阵中存在非对角元素不为零的情况，这导致输出之间存在交叉耦合影响，若引入解耦器则会增加控制器设计难度。因此，本文采用简单的控制技术，实现交叉影响最小化的目标。

2 模型预测控制

2.1 鲁棒性分析

由于在实际过程中存在各种不确定性因素，这导致所建立的理论模型和实际的被控对象之间存在着不可避免的失配，因此MPC的鲁棒性研究具有一定的实际意义。MPC的鲁棒性研究一般分为两种：MPC的鲁棒性分析和设计鲁棒MPC控制器。

MPC鲁棒性分析是指对标准MPC算法进行鲁棒性分析，虽然已忽略了模型中的各种不确定性因素，但这个过程仍然是比较困难的，不仅如此，文献给出的分析方法也屈指可数。文献[11]针对不确定脉冲响应模型，利用压缩映射原理计算出保证系统鲁棒稳定性的条件。文献[12]对带约束L1范数性能指标的MPC算法进行了研究，推导出保证系统鲁棒稳定性的条件。文献[13]分析了带输入约束的有限时域滚动优化控制算法的鲁棒性。

设计鲁棒MPC控制器，一种最经典的策略是采用Min-Max形式来优化控制设计，其基本原理是使目标函数值在不确定性集合中的最坏情况下达到最小。

2.2 输出预测

在MPC中，目标模型用于预测目标未来的输出，对于一般情况，存在干扰的对象模型以数学形式表示为

式中：xm和ym分别为状态方程和输出方程；Am，Bm，Cm分别为系统矩阵、输入矩阵、输出矩阵；Bξudist(k)为干扰量。

MPC的闭环结构框图如图2所示。在获得输出预测方程后，使用优化器为该目标提供最优的控制输入。本文所提SIDO Buck变换器的控制输入为开关管的占空比。

图2 MPC闭环结构框图Fig.2 MPC closed loop structure diagram

2.3 获得优化控制输入

3 仿真分析

3.1 无延迟仿真

使用MATLAB仿真软件对本文所提MPC算法进行仿真验证，仿真参数λ=1，α=1，预测范围和控制范围分别为20和2（预测范围的选择应确保其大于系统上升时间），其输出电压仿真结果如图3所示。图中，V1ref和V2ref分别为1 V和1.5 V，根据式（3）和式（4），可以计算出对应的占空比。在采样第50个Ts处，V2ref从1.5 V提高至2 V，V2紧跟随着参考电压，输出之间的交叉耦合影响小于±1%。

图3 SIDO Buck变换器引入MPC的仿真结果Fig.3 Simulation results of introducing MPC into SIDO Buck converter

从仿真结果分析得出，在多输出系统的情况下，采用MPC不但有效地减小了交叉耦合影响，还使变换器具有很好的电压跟踪性能。

3.2 延迟仿真

3.2.1 抗扰分析

为使仿真更加贴合实际，需要考虑延迟的影响。延迟环节在拉普拉斯域中表示为e-θs，在传递函数模块中可以表示为（1-θs），因为仿真是在离散域中进行的，所以z-k包含在增广状态矩阵中，其中k为延迟采样时间。同时，为了验证本文所提MPC的抗扰性能，使用表2所列仿真参数，在50%负载跳变情况下进行仿真，仿真结果分别如图4和图5所示。

表2 MPC设计参数Table 2 Design parameters of MPC

图4 支路1负载跳变50%的仿真结果Fig.4 Simulation results of 50% load jump of branch 1

图5 支路2负载跳变50%的仿真结果Fig.5 Simulation results of 50% load jump of branch 2

图4和图5中，V1和V2的参考输出电压均分别设置为1 V和1.5 V。从仿真结果来看，支路1和支路2在采样第50个Ts时发生50%负载跳变，V1和V2的电压调整范围均在8%以内，具有很好的抗负载扰动性能。

3.2.2对比分析

为了比较采用不同控制技术的变换器性能差异，以经典的PI控制技术作对比，使用表2所列仿真参数，仿真结果如图6和图7所示。其中，PI控制器的参数整定参考文献[14]中实现的数字控制器。

图6 使用MPC和PI控制的V1仿真结果Fig.6 V1 simulation results using MPC and PI control

图7 使用MPC和PI控制的V2仿真结果Fig.7 V2 simulation results using MPC and PI control

从仿真结果来看，由于控制器存在延迟的影响，导致两路输出电压会在最大过冲前出现下冲的情况。当V2ref出现30%的电压突变时，采用PI控制的V1的调整范围为7%；而采用MPC时，V1的调整范围仅有2%，且MPC的上升时间和稳定时间比经典PI控制器更短，即MPC暂态性能优于PI控制。经过分析，MPC的性能结果优于PI控制器的原因主要有两个：一是经典控制器由于延迟的影响，性能不是最优；二是目标模型的输出存在交叉耦合影响。

4 结论

为抑制SIDO Buck变换器输出之间的交叉耦合影响，本文在此变换器的基础上，提出了一种新型MPC算法。通过仿真对比分析了采用PI控制和MPC的SIDO Buck变换器，仿真结果表明，当电压发生扰动时，应用MPC的SIDO Buck变换器的电压调整范围是PI控制的1/3，证明MPC拥有比PI控制更好的交叉影响抑制效果和负载瞬态响应速度，充分验证了理论分析的正确性。