中间梁方式下压电式能量采集器发电性能研究
2022-04-18闫晓东周公博
闫晓东,周公博
(1. 江苏省矿山机电装备重点实验室,江苏徐州 221116;2. 中国矿业大学机电工程学院,江苏徐州 221116)
1 引言
目前,无线传感器节点在各种工业应用的监控系统中发挥着重要作用,可以在线监测关键设备的状态,进行故障检测和诊断等. 然而,传统的节点依靠电池供电,存在寿命短、定期更换困难(特别是矿井环境)等问题[1,2]. 随着能量收集技术的发展,从环境中获取能量正成为微电子设备持续供电的新途径. 因此,自供能节点变得越来越有吸引力. 环境中的能源包括太阳能、风能、振动能等. 其中,振动能几乎无处不在,且不易受天气、位置等因素影响,已成为研究热点[3]. 通常将振动能转化为电能的装置称为振动能量采集器. 根据能量交换原理,将振动能量采集器分为电磁式、静电式和压电式[4]. 而压电式能量采集器(Piezoelectric Energy Harvester,PEH)具有转换效率高、输出电压高、结构简单等特点,引起了人们的广泛关注[5].
常见的PEH 大多采用传统悬臂梁固定方式(Cantilever Beam Fixed Mode,CBFM),存在工作频带窄的问题,而环境激励频率具有宽频和随机性的特点,采集器的固有频率无法时刻匹配环境振动频率,导致采集器从环境中获取的能量密度小,发电性能大大降低[6,7].基于上述问题,许多学者提出了多种方法来提高PEH的发电性能和带宽[7],包括优化悬臂梁和质量块的几何结构[8~11]、优化电极的占比[12]、收集多种形式的能量[13,14]、引入非线性理论[15]、设计阵列式采集器[6]、引入自动调频技术[16]等. 其中,自动调频技术可以通过主动[17]或被动[18]的方式匹配环境振动频率,具有较强的环境适应性,表现出良好的发展前景. 但上述方法多是基于CBFM,存在可调频范围有限的缺点,即自由端无质量块时PEH 的固有频率为f,通过增加质量块,并利用自动调频技术,PEH 的固有频率可以在0~f范围内调节. 然而,很多大型装备存在两个或多个较稳定且离散的振动主频率,例如,大型振动筛的振动频率与物料的粒径和数目密切相关,即物料粒径和数目的不同会导致各振动主频率之间的差值变大. 当振动频率大于f时,PEH 在CBFM 下的发电性能将显著降低,从而达不到节点的功耗需求. 因此,传统CBFM 无法适用于环境振动频率变化范围较大的场合.
调整固定方式可以改变PEH 的固有频率,增加可调频范围,进一步利用自动调频技术来拓宽带宽以改善发电性能,提高PEH 的环境适应性. 然而,很少有学者研究PEH 的固定方式. 除了传统的CBFM,刘岳等[19]研究了固支梁固定方式,实现了结构的优化.Kodali 等[20]将固支梁方式下压电片分段布置,并通过实验进行了验证. Hamani 等[21]研究了在简支梁固定方式下,分布质量和不平衡质量对PEH 发电性能的影响. 然而,上述研究是对固定方式的单独研究. 另外,文献[22,23]研究了CBFM 和简支梁固定方式作用下,压电片的长宽比对PEH 的影响,并提出了一种新型固定方式,与CBFM 相比,该方法在更高的加速度激励下表现出更好的发电性能. 尽管对不同固定方式进行了研究,但PEH 在不同频段的最佳固定方式仍然不明确.
针对以上现状,本文提出了一种新型固定方式——中间梁固定方式(Intermediate Beam Fixed Mode,IBFM).相比于传统CBFM,所提出的IBFM 可以进一步通过自调频技术实现更宽的可调频范围,扩展PEH 的应用场合,提高其发电性能和环境适应性. 并试图确定在不同频段处PEH 的最佳固定方式,以最大限度获取能量.本文的主要贡献如下:
(1)证明了通过调整固定方式可以增加PEH 的可调频率范围,为拓宽PEH带宽提供指导;
(2)在保证压电片可以安全工作的前提下,研究了2 种固定方式下质量块重量变化时PEH 的发电性能变化趋势;
(3)验证了所提出的IBFM 在相同环境激励条件下与传统CBFM相比具有更好的发电性能.
2 模型与假设
2.1 模型
如图1所示,本文所使用的压电片模型在市场上很常见. 上下层为压电陶瓷,中间为CW617N 铜基板,压电陶瓷通过环氧树脂导电胶与铜基板胶结. 图1(a)为传统的CBFM,图1(b)为所提出的新型固定方式——IBFM. 与传统CBFM 相比,仅改变了固定端的位置,这是简单且容易实现的. 接下来,通过加入质量块,调整2 种固定方式的固有频率,分别研究2 种固定方式下PEH 的发电性能,从而确定不同频段的最佳固定方式.

图1 2种固定方式模型示意图
当自由端无质量块时,两种固定方式下的固有频率可以表示为

其中,m是单位长度的质量,YI 是梁横截面的弯曲刚度,L表示自由端距固定端的距离.2种固定方式的固有频率之间存在一定的关系,表示为

其中,L1与L2分别表示悬臂梁和中间梁2 种固定方式的自由端距固定端的距离,ωr1和ωr2分别表示悬臂梁和中间梁2 种固定方式的固有频率. 由于不同尺寸的压电片固定端的长度不确定,但一般远小于压电片的长度,因此可以先忽略固定端的长度,即认为L1=2L2. 假设CBFM 下PEH 的固有频率为f,可知调频范围为0~f,则采用IBFM后,调频范围可以增加至0~4f.
由于本文中2种固定方式的固定端长度均为1 mm,因此,在考虑固定端距离后,采用IBFM 时PEH 的调频范围可以达到0~3.1f.
其他相关参数见表1,其中压电层的弹性系数矩阵C、压电常数矩阵E和介电常数矩阵ε分别为

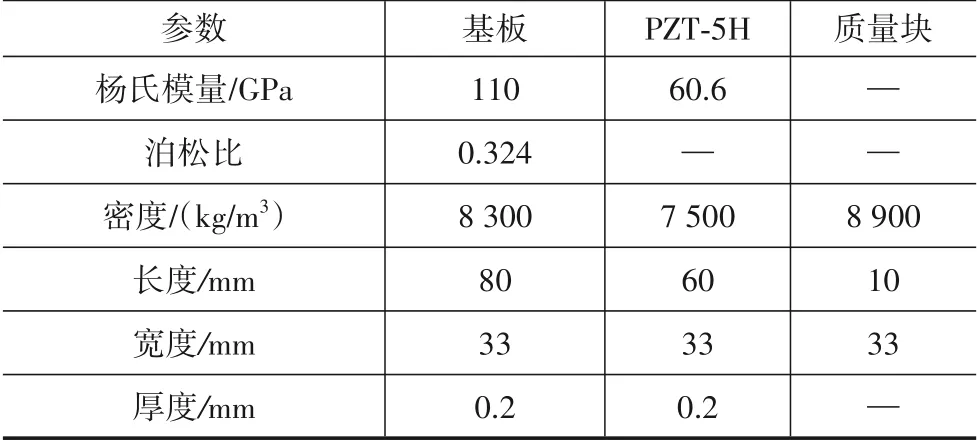
表1 模型参数
2.2 假设
通过调整质量块的重量可以改变PEH 的固有频率. 当外界环境频率大于f时,可以利用上述2 种固定方式,加入不同重量的质量块,将传统CBFM 下PEH 的调频范围从0~f扩大至0~3.1f.
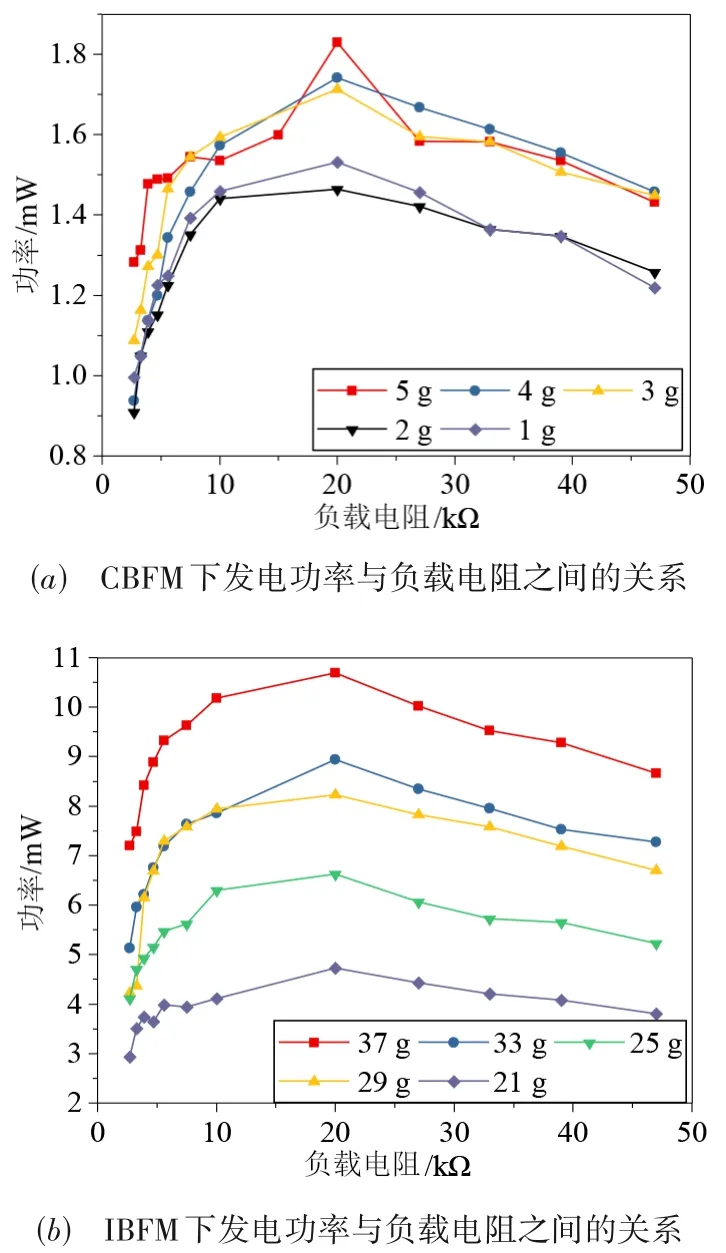
为了使能量获取最大化,需要确定不同频段的最佳固定方式. 选取13 组不同重量的质量块,范围为1~37 g,重量依次增加,质量块添加到自由端. 假设PEH在不同环境振动频率下的最佳固定方式如图2 所示,fmax和fmin分别表示最大和最小重量相对应的固有频率.可以假设CBFM 和IBFM 的调频范围分别为f1min~f1max和f2min~f2max. 随着重量的增加,IBFM 的固有频率不断降低,当f2min 图2 假设模型 本节主要模拟了PEH 在两种固定方式下相交频带处的发电性能. 仿真软件采用ANSYS 16.0,选取Solid5(压电材料)、Solid45(铜基板)、Circu94(电阻)3 种单元类型建立了PEH 的有限元模型. 首先,通过模态分析得到了固有频率. 然后,通过谐响应分析,得到了2 种固定方式下的极限加速度、极限位移以及最大开路电压. 此外,通过阻抗分析得到了机电耦合系数(Electro-Mechanical Coupling Coefficient,EMCC). 最后,在匹配最优电阻后,得到了2种固定方式下的最大发电功率. 频率特性是PEH 的重要指标,因为当环境振动频率与PEH 的固有频率一致或接近时,发电性能最佳.因此,研究固有频率具有重要意义. 为此,进行了模态分析,得到了CBFM 和IBFM 2 种固定方式随质量块重量变化的固有频率. 图3 为在2 种固定方式下,当重物的质量均为17 g 时PEH 的振型示意图,可以看出,两种固定方式下最大位移均发生在自由端. 图3 2种固定方式重物质量均为17 g时振型示意图 如图4所示,随着质量块重量的增加,2种固定方式的固有频率呈下降趋势. 当质量块的重量继续增加到一定范围时,固有频率的下降趋势减缓,说明当通过质量块调整频率时,质量块的重量不应过大. 质量过大可能导致刚度下降,使得压电陶瓷断裂,而压电陶瓷的断裂将大大削弱PEH 的发电性能. 同时,图4 显示CBFM 的固有频率均低于63 Hz,表明该固定方式适合于低频激励环境.IBFM 的固有频率高于CBFM,在48~200 Hz之间. 因此,IBFM更适合中低频激励环境. 此外,还验证了图2中存在相交频带的假设,CBFM和IBFM在48.24~63.90 Hz(f2min~f1max)频段内均可以达到谐振状态. 因此,下面将比较PEH 在相交频段不同固定方式下的发电性能. 图4 2种固定方式固有频率与重物质量的关系 在获取压电振子的最大开路电压之前,需要得到其极限加速度. 而压电陶瓷的极限应力一般为60~100 MPa[21],为了保证PEH的正常工作,以60 MPa为极限应力,进行谐响应分析. 激励载荷为加速度,加速度不断增大,直至最大应力为60 MPa 时停止,此时的加速度称为极限加速度,位移为极限位移. 图5 给出了2 种固定方式下加速度和应力之间的关系,可见随着加速度的增加,应力也随之增加,两者成正比. 图5 2种固定方式下应力与加速度的关系 图6 展示了在相交频带处PEH 所能承受的极限加速度随着质量块重量增加的变化趋势. 显然,两种固定方式下,随着质量块重量增加,所能承受的极限加速度均越来越小,但数值差别不大. 其中,CBFM 能承受的极限加速度较高,为9.26~15.18 m/s2;IBFM 能承受的极限加速度较低,为7.04~11.48 m/s2. 图6 2种固定方式极限加速度的比较 用k1表示极限位移与极限加速度的比值,即k1=d/a.如图7 所示,激励载荷为单位加速度条件时,与IBFM相比,PEH 在CBFM 下能产生更大的位移,但这并不意味着IBFM 发电性能较差. 因为当PEH 采用IBFM 并发生共振时,从图3 所示的2 种固定方式的振型图可以看出,IBFM 左右两端将产生相同的变形量且提供相同的发电量. 因此,2 种固定方式下PEH 的发电性能需要进一步研究确定. 图7 2种固定方式在单位加速度条件时的极限位移 通过谐响应分析,得到了PEH 在2 种固定方式相交频带处开路电压与加速度的关系. 如图8 所示,随着加速度的增加,开路电压均在不断增加. 同时,在相同加速度下,自由端质量块重量越大,开路电压越大. 其中,CBFM 和IBFM 下最大开路电压平均值分别为35.46 V 和53 V. 与CBFM 相比,采用IBFM 后,在相同加速度下产生的开路电压更高,提升了49.46%. 因此,对2 种固定方式分别添加不同重量的质量块后,在相交频带处,当激励加速度为极限加速度时,采用IBFM会产生更高的电压. 图8 2种固定方式开路电压与加速度的关系 最大开路电压是指在极限加速度条件下,PEH 产生的最大电压. 从图8 可以看出,在两种固定方式下,PEH 的最大开路电压数值差异很大. 为了直观比较两种固定方式下PEH 的发电能力,用k2表示最大开路电压与极限加速度之比,即k2=U/a. 如图9 所示,CBFM 和IBFM 下比例系数k2的平均值分别为3.128 2和6.105 9.因此,采用IBFM 时,PEH 在单位加速度的激励下能够产生更高的电压,且平均提高95.19%,也进一步说明调整固定方式可以提高PEH的发电性能. 图9 两种固定方式在单位加速度条件时的最大开路电压 EMCC是反映PEH机械能与电能耦合程度的参数,通常用来衡量PEH 的机电转换效率. Mason 等人[22]提出的计算方法被广泛用于计算共振频率附近的EMCC,其表达式为 其中,fa为开路谐振频率,fr为短路谐振频率. 由以上公式可以看出,为了得到PEH 的EMCC,需要求出开路和短路谐振频率,从而进行阻抗分析. 阻抗分析需要耦合电压,并将选定的平面合成为一个点. 其中双晶压电陶瓷上下通过导线并联连接. 实际上,阻抗分析是基于逆压电效应,即在交变电场作用下PEH 的机械变形. 为了便于计算,设置扫频范围,并将激励电场设为1V(简谐激励),结果即为阻抗. 假设简谐电场的激励为E=Emeiωt,压电片产生的电荷为Q=Qmeiωt,则阻抗表示为 其中,V(t)=Vm·eiwt,I(t)=dQ/dt=iwQmeiwt. 因此,阻抗进一步表示为 图10 所示为2 种固定方式下PEH 的阻抗和频率之间的关系. 从图中可以得到不同重物质量下PEH 的谐振频率,并根据式(3)计算出相应的EMCC. 从表2 可以看 出PEH 处 于CBFM 和IBFM 时,EMCC 分 别 分 布 在[0.35,0.43]和[0.45,0.53]. 经计算,CBFM 和IBFM 下EMCC 的平均值分别为0.394 8 和0.487 5,与CBFM 相比,采用IBFM 后,EMCC 平均提高了23.48%,PEH 的机电转换效率得到了进一步的提升. 表2 2种固定方式下EMCC 为了更深入地比较2 种固定方式在相交频带处的发电性能,本节研究了PEH 在2 种固定方式下的发电功率. 而获得最佳输出功率的前提是匹配最优电阻,只有当负载电阻和PEH 的内阻相等时,产生的功率才最大. 因此,需要设置一系列阻值不同的负载电阻进行匹配. 此外,匹配电阻范围可参照上述阻抗分析结果,PEH内部阻抗计算公式为 其中,θ为阻抗相位角,可以得出内阻值不会超过阻抗值的结论. 从图10 可以看出,在2 种固定方式下,PEH的阻抗值均不超过25 kΩ. 为了清楚地观察负载电阻变化时产生的功率,将负载电阻值范围设置为[0,50]kΩ,即通过设置不同大小阻值的负载电阻来测试PEH 的发电功率. 假设当前频率下外接负载电阻所对应的最大电压为Umax,而外接负载电阻在当前振动频率的电压可以表示为U=Umaxsin 2πft,则瞬时功率表示为 图10 2种固定方式的阻抗与频率的关系 最大平均发电功率的计算公式可以表示为 图11 所示为2 种固定方式下发电功率随负载电阻变化的情况. 观察表明2 种固定方式下PEH 的最佳匹配电阻阻值均在25 kΩ以下,这与阻抗分析得到的电阻阻值范围一致. 图12 展示了PEH 在2 种固定方式下发电功率随激励加速度变化的趋势,可以看出随着加速度的增加,发电功率也在增加,但在2 种固定方式下发电功率的数值差异较大. 在相同的加速度下,PEH 在采用IBFM 时发电功率要比采用CBFM 时大得多. 其中,处于CBFM和IBFM时最大平均发电功率的平均值分别为8.26 mW 和19.24 mW. 可见在采用IBFM 后,最大平均发电功率提高了132.93%. 图11 两种固定方式的最优负载电阻 图12 2种固定方式的发电功率与加速度的关系 最大平均发电功率表示匹配最佳电阻后,在极限加速度激励条件下,PEH 产生的功率. 由于2 种固定方式在相交频带处极限加速度不完全相同,因此需要通过计算最大发电功率和极限加速度的比例系数k3来比较最大发电能力,即k3=Paverage/a. 如图13所示,显然,当PEH采用IBFM时,单位加速度激励条件下产生的发电功率远高于CBFM时的发电功率. 其中,CBFM和IBFM下比值系数的平均值分别为0.712 9和2.180 6.说明采用IBFM后,单位加速度激励下PEH的最大发电量提高了205.88%. 图13 2种固定方式在单位加速度条件时的最大发电功率 因此,结合上文中开路电压和EMCC的比较结果可知:在2 种固定方式下,IBFM 可以提供更好的发电性能. 此外,参考图12和13还可以看出,在相同的加速度条件下,随着质量块重量的增加,PEH 的发电功率也随之不断增加. 然而,有趣的是,PEH 的最大平均发电功率整体呈现下降趋势. 事实上,从图6 可以看出,重物的质量越大,PEH 能够承受的极限加速度越小,这对PEH的最大平均发电功率有直接影响. 实验部分主要对仿真结果进行验证. 首先求解出相交频带;其次对2 种固定方式下PEH 的开路电压进行研究;然后,通过阻抗分析得到了EMCC,并参考阻抗分析结果匹配最优负载电阻;最后,进行最大平均发电功率的实验. 分别对PEH 在2 种固定方式下进行了不同重物重量的实验,搭建了如图14所示的实验平台,所涉及的实验设备主要有S51110高能电动式激振器、BAA120功率放大器、SCS-2 信号发生器以及示波器. 其中,2 种固定方式下,质量块均由镍材料制成,压电片尺寸完全相同,只是改变了固定方式. 通过参考仿真得到的2 种固定方式的固有频率值,设置相应的扫频间隔,进而利用激振器进行扫频得到PEH 的固有频率. 在扫描过程中,观察示波器的电压变化并记录最大开路电压时的频率,对应的频率认为是固有频率. 图14 实验平台 图15给出了两种固定方式下的固有频率随重物重量的变化趋势. 结果表明,两种固定方式下的固有频率随重物重量的增加而减小,与仿真结果一致.CBFM 下的固有频率普遍处于46.28 Hz 以下,而IBFM 下的固有频率处于39.6 Hz 以上. 同时,CBFM 和IBFM 在34.1~51.9 Hz(f2min~f1max)之间相交,再次验证了图2 提出的假设. 接下来将通过实验对PEH 在2 种固定方式相交频带处的发电性能进行比较. 图15 2种固定方式的固有频率与重物质量的关系 当激振频率与PEH 固有频率一致且所施加的加速度为极限加速度时,对应的开路电压是最大开路电压.依次测量2 种固定方式在不同重物质量下的最大开路电压,结果如图16 所示,可以看出,2 种固定方式下开路电压均随着加速度的不断增大而增大,且在加速度相同的条件下,重物质量越大,PEH 所产生的开路电压也越大. 其中,CBFM 和IBFM 下最大开路电压平均值分别为24.304 V 和42.154 V. 相比于CBFM,PEH 在IBFM 下产生的最大开路电压要更高,平均提升了73.44%. 图16 两种固定方式的开路电压与加速度的关系 如图17 所示为单位加速度条件时CBFM 和IBFM两种固定方式在相交频带处产生的最大开路电压,比例系数k2的平均值分别为2.148 6 和4.845 6. 显然,IBFM 产生的开路电压更高,相比于CBFM,比例系数k2平均提升了125.52%. 采用IBFM 后,在相交频带处,PEH有更好的发电性能,同时也验证了仿真的正确性. 图17 2种固定方式在单位加速度条件时的最大开路电压 在进行发电功率实验之前先进行阻抗分析,目的是为接下来匹配最优负载电阻提供参考. 如图18 所示,所使用的实验仪器为WK6500B 阻抗分析仪,由于阻抗分析需要对PEH 施加1V 的正弦电压,根据逆压电效应,压电片会产生振动. 因此,在实验过程中需将PEH 固定在台面上,以免引起支座抖动而影响PEH 的振动状态,从而产生一定的误差影响. 图18 阻抗分析实验 图19 展示了2 种固定方式的阻抗随频率变化的趋势,可以看出,两种固定方式的阻抗值均处于50 kΩ以下. 得到不同重物质量时PEH 的谐振频率后,根据式(3)计算EMCC. 表3 为2 种固定方式在不同重物质量时的EMCC,可见CBFM 和IBFM 在相交频带处EMCC 的平均值分别为0.337 8 和0.377 0. 相比于CBFM,采用IBFM 后,PEH 的EMCC 平均提升了11.60%.进一步验证了仿真结果的正确性,同时,也证明了所提出的固定方式可以使PEH 的机电转换效率进一步提升. 图19 2种固定方式下阻抗与频率的关系 表3 2种固定方式下EMCC 与仿真方法测试发电功率类似,在进行发电功率实验之前,需要根据实验所测得的阻抗值设置一系列阻值不同的负载电阻进行匹配. 得到最优负载电阻值后,施加相应的极限加速度,此时产生的功率即为最大平均发电功率. 其中,负载阻值的设置参照4.3 节阻抗分析得到的结果,取0~50 kΩ 之间的仿真电阻进行实验. 图20 所示为两种固定方式的最优负载电阻. 可以看出,2 种固定方式下,最优阻值均为20 kΩ,接下来将进行最大平均发电功率的测试和比较. 图20 两种固定方式的最优负载电阻 图21 展示了2 种固定方式下发电功率与加速度之间的关系. 在相同加速度条件下,2 种固定方式的发电功率都随着重物质量的增加而增加. 而随着加速度的不断增大,PEH 在2种固定方式下的发电功率都在不断增大. 此外,与仿真结果类似,PEH 的最大平均发电功率随着重物质量的增加整体呈下降趋势. 其中,CBFM和IBFM 的最大发电功率平均值分别为6.723 mW 和21.770 mW,相比于CBFM,在相交频带处,PEH 在采用IBFM后,最大平均发电功率平均提升223.81%. 图21 2种固定方式的发电功率与加速度的关系 2 种固定方式在单位加速度条件下产生的最大平均发电功率如图22 所示,CBFM 和IBFM 在相交频带处,比例系数k3的平均值分别为0.576 4 和2.470 4. 相比于CBFM,PEH 在采用IBFM 后,单位加速度条件下最大平均发电功率平均提升328.59%. 图22 2种固定方式在单位加速度条件时的最大发电功率 综上所述,相比于传统CBFM,所提出的IBFM 在调频范围以及发电性能两方面都表现的更加优越. 同时,所提出IBFM 的最大可调频范围达到了传统CBFM 的3.1 倍以上,有效拓展了PEH 的带宽. 如表4 所示,在2种固定方式的相交频带处,当激励载荷为单位加速度时,相比于CBFM,所提出IBFM 的开路电压和发电功率分别平均提升了125.52%和328.59%. 此外,EMCC 平均提升了11.60%,进一步说明了改变固定方式后提升了PEH 的发电性能. 因此,在相交频带处,PEH 采用IBFM后发电性能更佳. 表4 2种固定方式在相交频带处性能参数比较 本文提出了一种新型固定方式——IBFM,所提出的方法不仅有效拓宽了传统CBFM 下PEH 的可调频范围,大幅提升了其发电性能,而且具有普适性,可用于任意尺寸的压电片. 仿真和实验结果表明:所提出的方法可以将传统CBFM的可调频范围从0~f拓宽至0~3.1f以上. 与传统CBFM 相比,采用IBFM 后,在2 种固定方式的相交频带处,单位加速度激励条件下PEH 的最大开路电压和最大平均发电功率分别平均提升了95.19%和205.88%. 同时,EMCC 平均提升了11.60%. 验证了改变固定方式可以改善PEH 的发电性能,为不同频段固定方式的选择提供了指导,说明在实际应用中通过改变PEH 的固定方式来拓宽带宽和提高发电性能是可行的.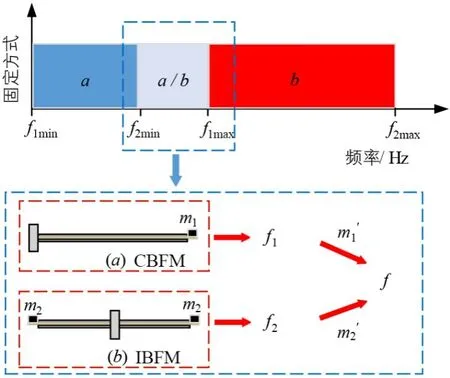
3 相交频带处发电性能仿真研究
3.1 相交频带的求解


3.2 最大开路电压
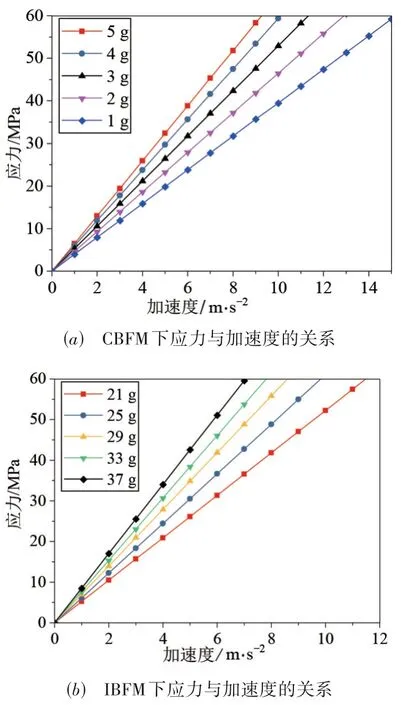

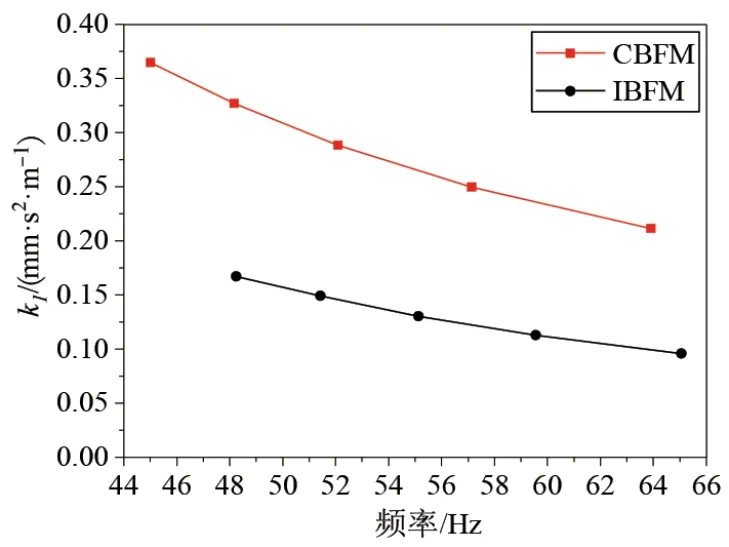
3.3 机电耦合系数


3.4 最大平均发电功率




4 相交频带处发电性能实验验证
4.1 相交频带的求解

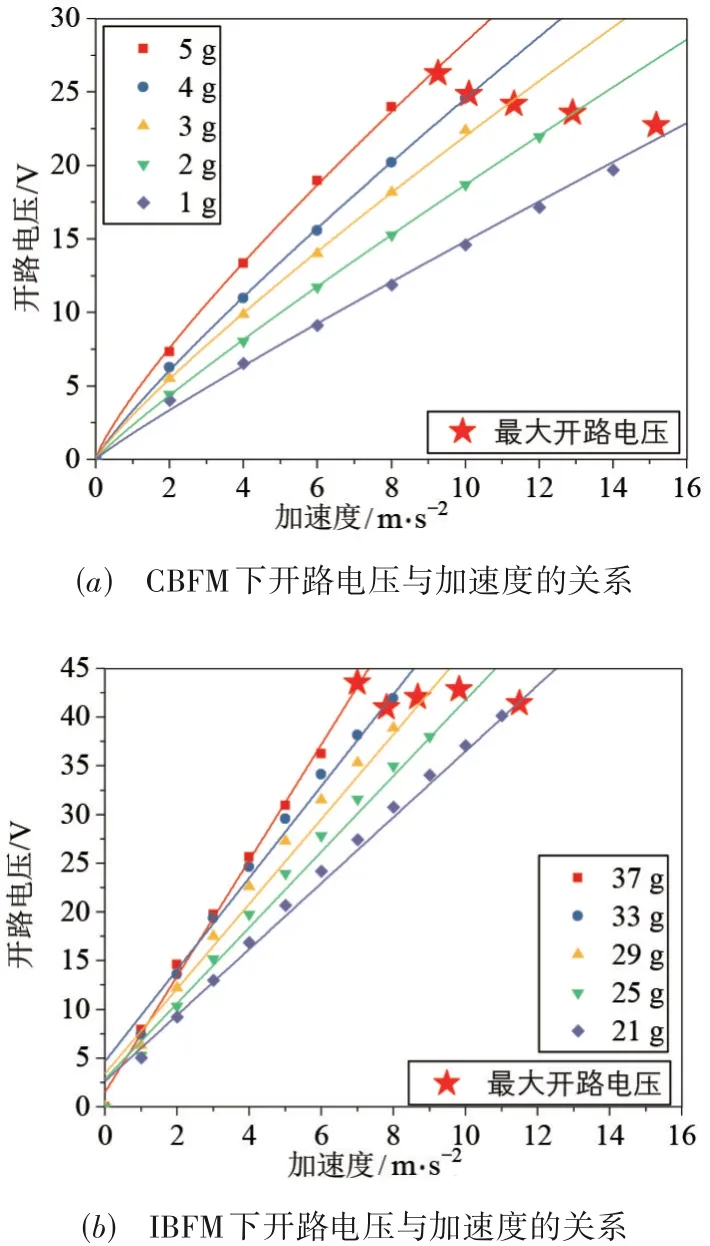
4.2 最大开路电压
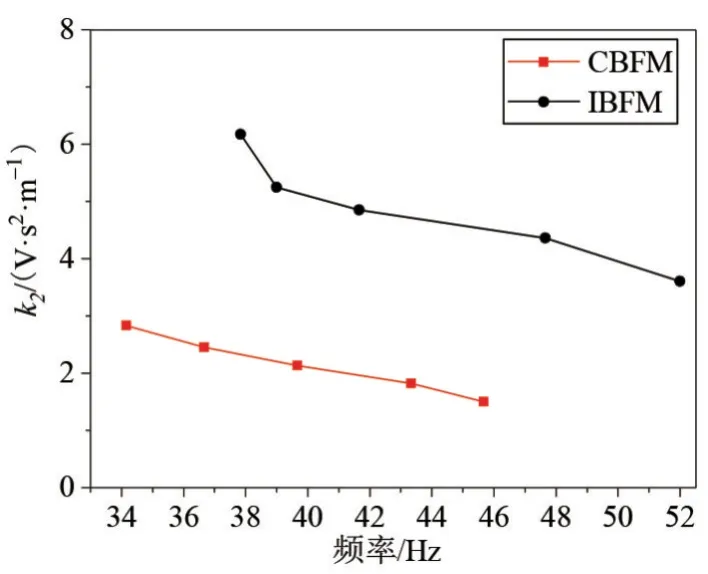
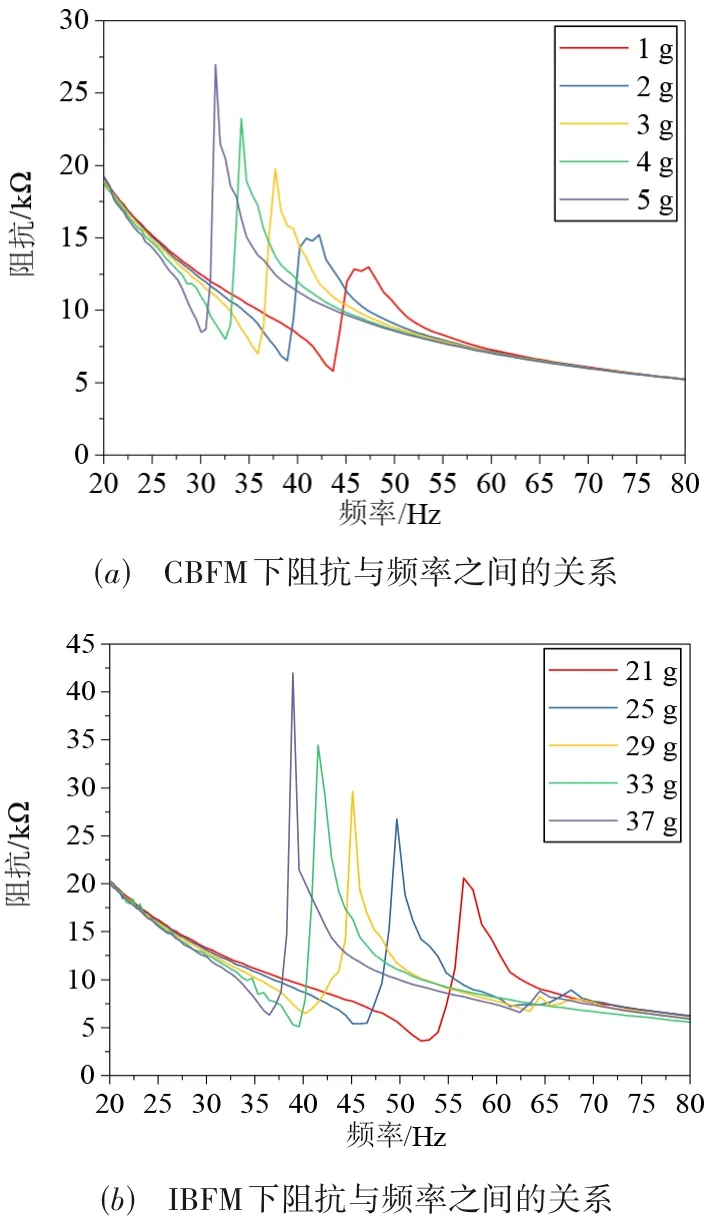
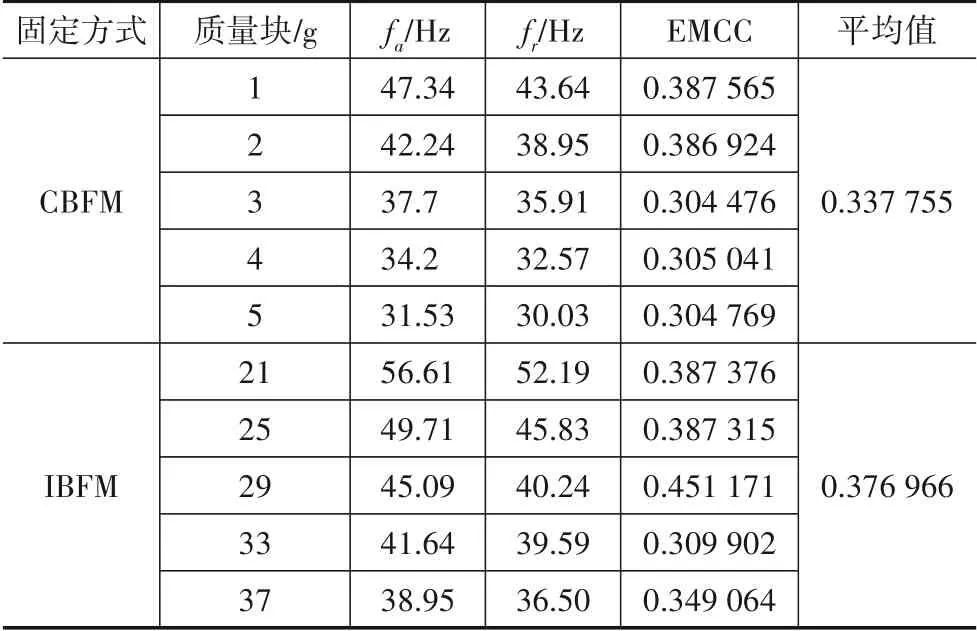
4.3 机电耦合系数

4.4 最大平均发电功率



5 结论
