参数自适应的析取云模糊置信规则识别方法

李双明，关 欣，王海滨

（1. 海军航空大学,山东烟台 264001；2.92941部队,辽宁葫芦岛 125001）

1 引言

数据分类在机器学习和数据挖掘中扮演着重要的角色，已有的数据分类方法大致可分为两种：“黑箱”方法和“白箱”方法.“黑箱”方法有支持向量机［1］、神经网络［2］以及它们的各种扩展方法［3］，“白箱”方法有K 近邻算法［4］、贝叶斯方法［5］、决策树方法［6］、模糊分类法［7］等. 由于复杂的电磁环境、测量设备的系统误差或测量手段的缺乏，不可避免地获得“低质量”的数据，这些数据往往呈现出不确定性，如模糊性、不精确性、不完备性，甚至数据缺失.

使用不确定知识表示和推理的三个最常见的框架是：贝叶斯概率理论［8］、Dempster-Shafer 理论［9］和模糊集理论［10］. 在知识表达系统中，最常见的知识系统为基于规则的系统，其大致分为三种：粗糙集［11］、决策树［6］以及基于“if-then”形式的规则［12］. 在简单“if-then”规则基础上发展而来的模糊规则分类系统（Fuzzy Rule-Based Classification System，FRBCS）已经成为处理分类问题有效的工具之一［13］，但是推理过程采用平均加权策略，决策方法采用“单赢”策略，不能够处理不完备的信息，且受样本噪声的影响较大. 文献［14］对FRBCS进行了扩展，但该方法也没有实现对不完备信息的建模. 杨剑波教授基于D-S 理论、决策理论和模糊集理论，提出了以置信结构建立混合规则库、以证据推理（Evidential Reasoning，ER）为推理机的新方法［15］，该方法能够实现对不完备信息的建模，但是对于分类问题而言，该方法出现规则数量“爆炸”现象. 文献［16］提出了前提部分也嵌入置信结构的分类系统，该方法的规则数和训练样本数是相等的，在识别时会增加计算负担. 焦连猛提出了带有置信结构的模糊规则分类系统［17］，该模型结合了置信结构和模糊集的各自优点，引入了特征权重，提出了数据驱动的置信规则库（Belief Rule Base，BRB）建模方法，该方法充分利用训练数据来映射特征空间和类空间的不确定联系，有效降低噪声数据对分类结果的影响.

尽管上述基于各种模糊规则的识别方法都有各自的优势，但同时也存在不足，其中最重要的问题为规则的可解释性. 文献［17］指出影响规则可解释性的主要原因包括规则结构、规则数量、特征数量、模糊划分的数量、模糊集的形状，其中规则结构包括特征属性的逻辑连接关系、特征属性权重、规则权重、规则前提部分的分布结构、规则结论部分的分布结构、规则结论的生成方式等. 为此，本文提出了参数自适应的云模糊置信规则识别方法.

2 析取云模糊置信规则识别系统

析取命题下的云模糊置信规则为

其中，Rq表示第q条规则，其规则权重为θq，属性权重为δ1，δ2，…，δP，q=1，2，…，Q，Q为 置 信 规 则 库 中 规 则的数量，P为前提属性的数量，M为推理结论的数量，x=(x1，x2，…，xp)T为模式特征向量，为云模糊集，每 个 属 性 模 糊 划 分 集 为，规则权重0 ≤θq≤1，属性特征权重0 ≤δp≤1，满足=1.

析取云模糊规则识别系统需要解决以下几个问题：模糊集的划分、规则的产生、规则参数的确定. 在无先验知识的前提条件下，本文研究如何从数据自身来实现系统建模，因为系统结构及参数均基于传感器测量的数据而得到，并根据识别结果对其进行调整，故称为参数自适应的析取云模糊规则分类系统. 系统结构如图1所示.

图1 参数自适应的云模糊规则识别系统结构图

2.1 特征域的模糊划分

2.1.1 基于频数的双门限检测方法

定义1对于描述某种特征属性的数据集合H={Hi|i=1，2，…，m}，记y为集合H中的元素Hi出现的个数，称y=f(Hi)为数据集合H的频数分布函数，则有式（2）成立，即

其中，n为数据样本总量.

设置频率检测门限（数据点的频数与数据总量的比值）为δ，当统计数据点的频数满足式（3）时，保留该数据分割点，否则放弃该数据分割点.

当两个数据分割点出现的频数都超过阈值且相距较近，从聚类的角度，这两个数据点应该为同一类数据，因此有必要舍去其中的一个数据点.

定义2记相邻的两个数据分割点为Hi和Hi+1（i=1，2，…，l，l≤m-1 ≤n-1），称式（4）为两个数据之间的分离度.

设置分离度检测门限为λ，若经过频率检测门限δ检测后相邻两个数据分割点的分离度满足式（5），即

那么，舍去其中的一个点，其原则为：将通过频率检测门限的数据点升序排列，首先计算第1 个点和第2 个点的分离度，若满足，则舍去第2 个点，然后计算第1 个点和第3 个点的分离度，依次往下；否则，第1 个点和第2个点都保留，然后计算第3个点和第4个点，依次往下.

2.1.2 基于包含度的双门限检测方法

根据数据聚类的思想，将聚类中心作为模糊域划分点. 文献［18］提出了基于数据包含度的自动聚类算法，该算法是一种基于密度的聚类算法，将自身数据密度大，且离其他数据点相对较远的数据点作为聚类中心. 对于数据个数较多时，上述方法耗时较大，基于上述方法，本文提出了改进的包含度检测方法，步骤如下.

步骤1：将整个数据集升序排列可得x′1，x′2，…，x′n.

步骤2：以第一个数据点x′1为起始点，依次计算下一个数据x′i(i＞1)与x′1之间的距离d(x′i，x′1)，若小于截断距离dc，则将x′i和x′1划为一组，记为S，若d(x′i，x′1)大于截断距离dc，分组停止.

步骤3：计算包含度|S|/n，若| S |/n小于给定的包含度阈值uc，则舍去该组数据，否则保留，记为S1.

步骤4：以第x′i+1为起始点，依次计算下一个数据x′j(j＞i+1)与x′i+1之间的距离d(x′j，x′i+1)，执行步骤3，得到St，遍历整个数据，执行步骤5.

步 骤5：通 过 步 骤1～4 后，得 到n′组 数 据St(t=1，2，…，n′)，以mean(St)作为模糊域的分割点，n′作为模糊域的划分数量.

2.2 云模糊集

本文以二阶正态云模型作为模糊集样式［19］，相比于三角形模糊集样式，其具有以下优势：

（1）能够刻画数据的正态分布特性；

（2）能够解决模糊集覆盖有限的问题；

（3）能够调整参数改变模糊集的形状.

设模糊域分割点为{p1，p2，…，pl}，相应地确定了l个云模型，按式（6）计算每个云模型的参数.

其中，ken和khe为常数，称为熵和超熵系数，决定了云模型的形状.

2.3 模糊规则库

2.3.1 规则的前提部分

对训练样本x=(x1，x2，…，xn)T，xi对应第i个特征属性上的测量值，根据第2.1节中特征域上的云模糊集划分，遍历xi隶属于第i个特征域的云模糊集合=的隶属度，取每个特征域最大隶属度对应的云模糊集组合为一条规则的前提条件，在规则前提条件确定的过程中，同时也确定了支持该规则所包含的训练样本.

2.3.2 结论部分的置信结构

设第q条规则Rq包含的训练样本子集为Sq，类标签集为Ω={ω1，ω2，…，ωM}，集合Sq中的第i个训练样本为xi=(xi1，xi2，…，xiP)T，在每个特征上的隶属度分别为，样本xi与前提部分的匹配程度为

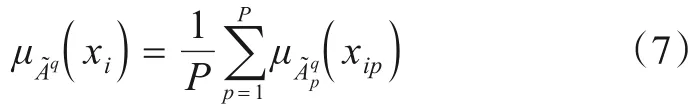
文献［17］将Ω={ω1，ω2，…，ωM}作为辨识框架，对于Sq中每一个训练样本xi，把类别Class(xi)=ωm当作支持ωm为对应规则结论部分的一个证据. 在证据理论框架下，将μq(xi)作为ωm类的基本概率分配，由于该证据只支持ωm，不支持其它的任何一类，因此除ωm外的其他类基本概率分配为零，将剩余置信1-μq(xi)分配给整个辨识框架Ω，该证据用下面的mass 函数来表示，即

其中，0 ＜μq(xi) ≤1.

同样地，得到Sq中所有样本生成的证据，利用Dempster 组合规则进行融合，得到融合后的mass 函数mq，那么规则Rq的结论部分置信度为

当一个前提部分包括不同类别的数据样本时，生成的证据之间是高冲突的，用上面的组合规则进行融合是不合适的. 下面以两类数据进行说明.

例1假设第q个前提组合包含n个数据样本，分为ω1和ω2两类，ω1类的样本数为n1，ω2类的样本数为n2，满足n1+n2=n.

ω1类的样本xi生成的mass函数具有如下形式，即

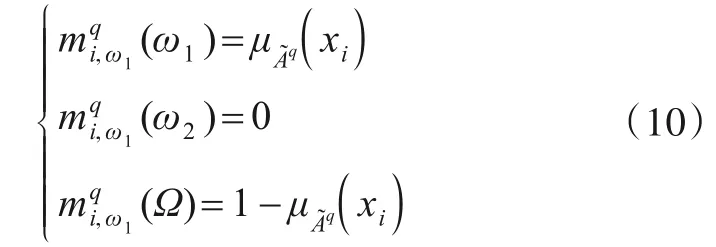
按照上面的方法，产生ω2类的mass函数.

Dempster 组合规则具有交换律的特点，分两种情况进行组合.

（1）先对ω1类样本生成的证据进行组合，当n1≥N1时，所有证据的组合结果为

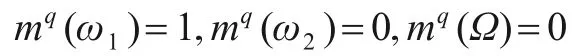
显然该证据得到的置信结果是不符合逻辑的，完全丢弃ω2类的样本对置信度的贡献.

（2）先对两类证据分别组合，当n1≥N1，n2≥N2时，有

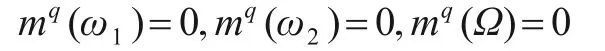
显然这样的结果是错误的.

为此本文提出了一种基于可靠度的置信结构生成方法.

定义3设第q个前提组合包含的样本数为n，类ωm的样本数为nωm，则结论部分类别ωm置信度的可靠度为

式（10）引入可靠度进行修正，得

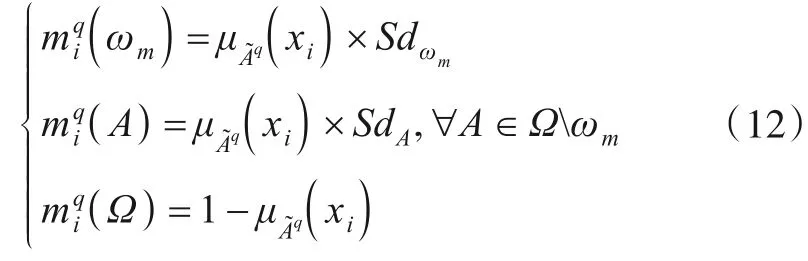
式（12）是一种新的基本概率赋值，可以看做是广义的证据源修正，然后根据Dempster 组合规则进行融合，得到结论部分的置信结构分布.

2.3.3 规则权重和特征权重的优化模型

记目标函数为

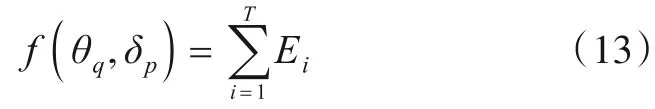
其中，T为训练数据集的大小. 对每一个样本，若系统识别结果正确，Ei=0，否则Ei=1. 则优化目标模型为

2.4 推理算法

2.4.1 规则激活

设y=(y1，y2，…，yP)T表示要分类的未知目标. 该目标的特征测量值或者是完备的，或者缺失某些特征测量值. 如果某些特征测量值缺失，那么属于相应模糊划分域的匹配度为零，采用加权平均算子获取未知目标在规则Rq模糊域Aq上的匹配度为

μAq(y)的值尽管很小，但总不为零，所以有必要设置规则激活阈值σ，当且仅当μAq(y) ＞δ时，规则Rq才被激活，否则不被激活.σ用于控制被激活的规则数量，σ的取值不同，激活的规则数量也不相同.σ的取值越小，被激活的规则数量就越多，直至规则库中所有的规则被激活. 那么该如何选取σ呢？可以根据实际情况，对σ的取值主观设定. 对于正态云而言，99.7%的云滴都落在[Ex-3En，Ex+3En]的区间内，即云模糊集的绝大部分贡献都处于[Ex-3En，Ex+3En]区间内. 所以σ的取值可以设定为边界点Ex-3En和Ex+3En对应的隶属度，近似地，本文取σ=e-4.5≈0.011 1.

设Q′表示被未知目标y=(y1，y2，…，yP)T激活的规则集，有

规则Rq的激活度αq由两个因素决定：匹配度μAq(y)和规则权重θq.μAq(y)反应了未知目标与置信规则前提部分的相似程度，θq反应了置信规则的稳定程度. 定义

2.4.2 推理决策

用Shafer 的折扣算子对激活的置信规则进行折扣，有

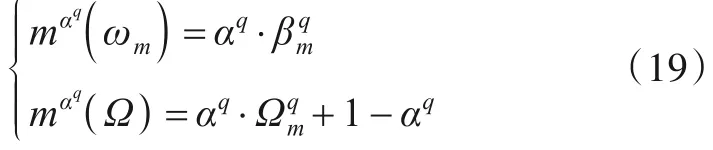
用Dempster 组合规则对激活的规则进行组合，对任意mαq( ·)，及mαq(Ω) ≠0 外，其他元素的基本概率赋值都为零，Q′个组合规则的解析表达式为

其中，K表示归一化系数，q=1，2，…，Q′，m=1，2，…，M.

采用置信度最大的原则进行决策，即

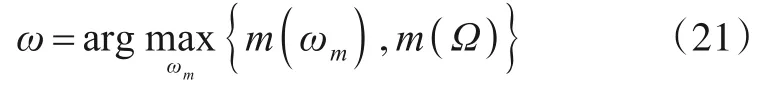
则ω为识别结果.

3 实验验证

3.1 仿真数据验证

以电子侦察系统中的雷达辐射源识别为例，对本文所提方法进行验证. 设有3类雷达，选择射频频率（Radio Frequency，RF）、脉冲重复间隔（Pulse Repetition Interval，PRI）和脉宽（Pulse Width，PW）作为雷达的特征参数，各类雷达每种特征属性上的测量值服从正态分布，各类雷达特征参数见表1. 每类雷达仿真生成两类正态随机数据：一类具有统计特征分布，用来验证频数检测方法：一类不具有统计特征分布，用来验证包含度方法. 在两类数据中，每种雷达各有200 个样本，共计600 个数据样本，并以该数据作为训练数据，进行系统建模. 为消除量纲的影响，仿真中用到的数据进行了归一化处理.

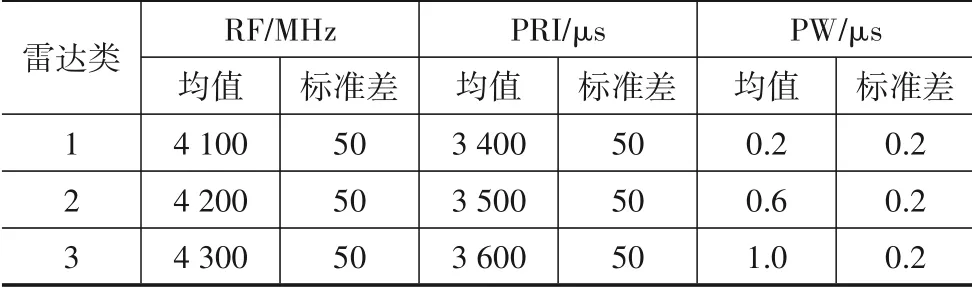
表1 雷达特征参数

3.1.1 正确识别率分析

当识别系统建好后，用两种测试数据进行测试：一种是以训练数据作为测试数据（无噪声）；另一种是在训练数据集内随机抽取，并分别叠加2%，5%，10%，15%，20%的干扰噪声生成测试数据. 对这两种测试数据，分别进行1 000 次Monte Carlo 实验，其仿真结果如表2 所示. 表2 中，数据1 表示具有统计分布特征的仿真数据，数据2表示无统计分布特征的仿真数据.

表2 正确识别率/%

系统云模型的参数设为ken=1.2，khe=0.001. 不同的门限参数，模糊域划分的数量是不同的. 模糊域划分（3，3，4）表示特征RF、PRI 和PW 上的模糊分割数为3个模糊集、3个模糊集和4个模糊集.

对于数据1，训练数据集上的识别结果要优于含有噪声的测试数据集，并随着噪声的增大，正确识别率逐渐降低，当加入20%的噪声时，3 种模糊划分的正确识别率是最低的，分别为73.1%，79.9%，84.4%. 无论是训练数据集还是含有噪声的测试数据集，随着模糊域划分的精细，即划分的模糊集数量增多，正确识别率逐渐增大，对于数据2 也有同样地结论. 此外，在模糊划分数基本相同的情况下，数据1 的识别结果要差于数据2的识别结果，例如，当数据1 和数据2 中的模糊域划分都为（3，3，4）时，数据2 的正确识别率要比数据1 高7.5%～18.51%，其他的模糊域划分也是如此. 其原因为，尽管数据1 和数据2 的样本总量是相同的，但在同种特征属性上，样本数量是不同的，数据1 的样本量要明显小于数据2 的样本量，因此相对地讲，数据1 的样本量是小于数据2 的样本量的，所以会出现表中的结果. 表2 中只给出了部分不同模糊划分下的识别结果，缺少对相关参数的敏感性分析，在3.1.2节中讲述.

3.1.2 参数敏感性分析

选取3.1.1节中的数据作为训练数据集，可调节的参数包括包含uc，dc，ken，khe，δ和λ. 下面给出各参数的取值范围及变化步长：

（1）0.07 ≤uc≤0.16，变化步长0.005；

（2）0.07 ≤dc≤0.16，变化步长0.005；

（3）0.8 ≤ken≤3.8，变化步长0.25；

（4）0.01 ≤khe≤0.5，变化步长0.01；

（5）0.04 ≤δ≤0.06，变化步长0.001；

（6）0.1 ≤λ≤0.6，变化步长0.05.

仿真结果随参数变化情况如图2所示.

图2（a）中，随着包含度的增大，正确识别率呈现先下降后上升的“凹陷”现象. 当包含度uc为0.125，0.13 和0.135 时，正确识别率是最小的，约为92%；当0.07 ≤uc≤0.115 和0.14 ≤uc≤0.16 时，正确识别率都比较高. 进一步分析，当包含度为0.12，0.125，0.13，0.135和0.14 时，其模糊域划分分别为（5，4，3）、（4，4，3）、（4，4，3）、（4，4，3）和（4，3，3），划分（5，4，3）多于划分（4，4，3），识别率高，而划分（4，3，3）少于划分（4，4，3），识别率也高，说明识别率并不随着划分的数量增多而得到改善，而是存在一个最优的组合. 图2（b）中，尽管不同的截断距离上的识别结果是不同的，也不存在固定的变化规律，但是识别率都在99%以上，说明截断距离对识别结果的影响是最小的. 图2（c）中，正确识别率随着熵系数的增大逐渐降低. 图2（d）中，随着超熵系数的逐渐增大，识别结果呈“震荡”式变化，在超熵系数为0.39 以及0.45 时，出现了明显的“断崖”式下降，因此在选择该参数时，应当尽量地避开这些点，可以选择较小的数值. 图2（e）和图2（f）中随着检测门限的提高，系统的识别性能都呈现下降趋势，因此在选择这两个参数时，可以考虑选择较小的数值.

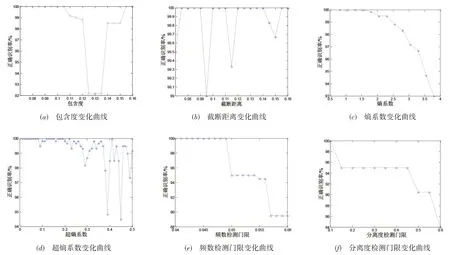
图2 仿真结果随参数变化情况

3.2 实测数据集验证

利用UCI中的实测数据集，将本文方法与模糊置信规则分类系统（Belief Rule-Based Classification System，BRBCS）、支持向量机（Support Vector Machine，SVM）、核函数极限学习机（Kernel Extreme Learning Machine，KELM）等方法进行对比分析，采用B-折交叉验证（BFold Cross-Validation，B-CV）的方法计算正确识别率，本文选用5-折交叉验证. 实验中选用Iris，Banknote，Ecoli，Seeds 及Haberman 5 类数据集，每类数据集的样本数量、属性数量和类别数量详见表3.

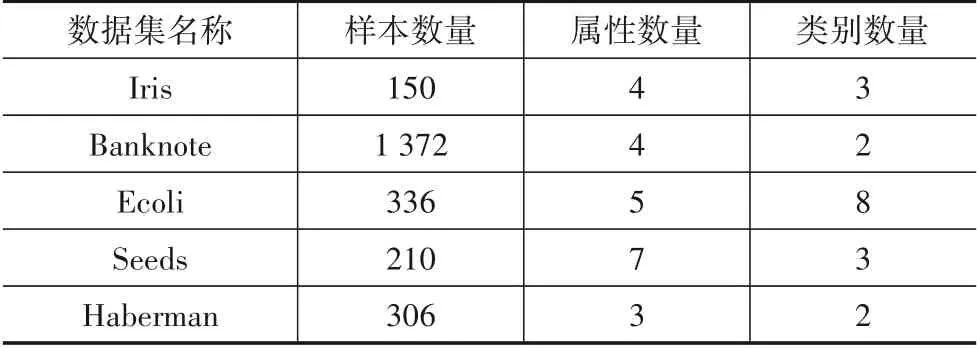
表3 数据集信息描述

在支持向量机分类方法中，其惩罚系数为1，核系数为0.01，核函数为RBF 核. 在核函数极限学习机分类方法中，其惩罚系数为1，核系数为1，核函数为RBF核. 本文中的熵系数和超熵系数分别为1.2和0.001. 仿真实验结果见表4.

在BRBCS方法中，因为无先验知识，采用简单的模糊格主观划分方法，且每个属性上的划分数相同，划分情况分为3种情况：每个属性划分为3个模糊集、5个模糊集和7个模糊集. 从表4中可知，对同种数据集而言，并不是划分的数量越多，识别结果就越好. 在Iris，Haberman 以及Banknote 数据集上，精细的模糊域划分提高了识别结果；但是在数据集Ecoli 和Seeds 上，精细的模糊域划分，反而降低了系统的分类性能. 这说明BRBCS 分类系统的识别系统与模糊域的划分没有规律可循，若要得到较优的分类性能，需要主观反复地进行验证，以此来确定满足系统较优分类性能的模糊域划分. 在实际应用中，尤其对实时性有一定要求的场景，显然该方法是比较消耗时间的.

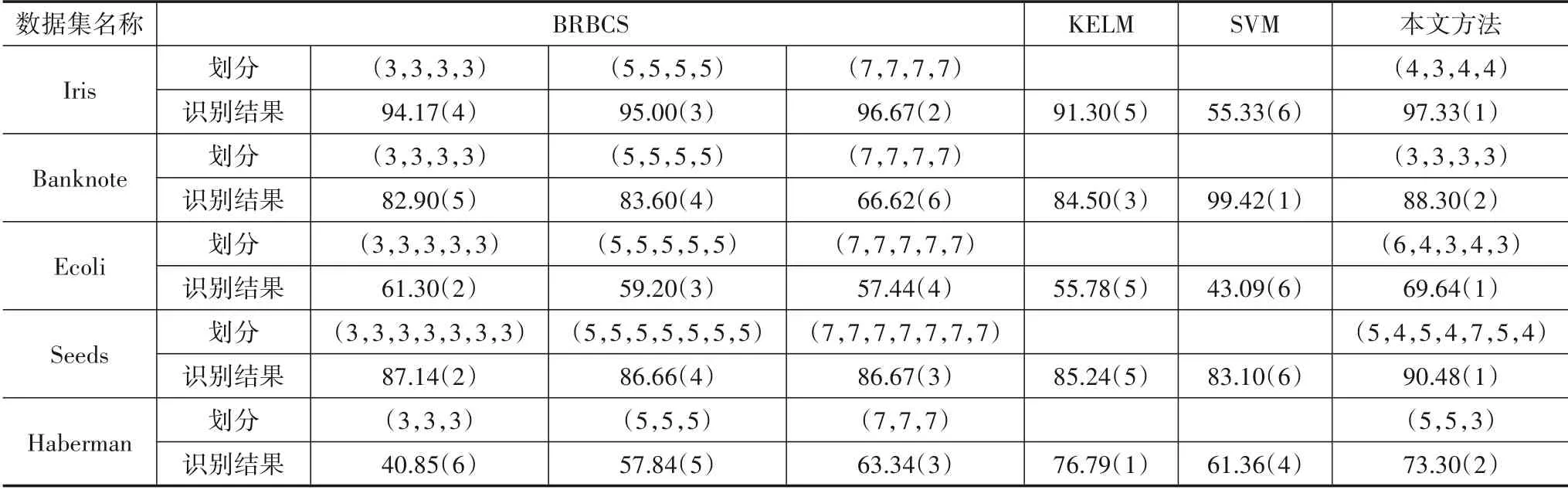
表4 正确识别率/%

KELM、SVM 方法在5 种数据集上的总体识别结果要差于本文方法，但存在例外，SVM 方法在Banknote 数据集上的识别结果在所有方法中是最好的，KELM 方法在Haberman 数据集上的识别结果是最优的. 造成这种结果的原因主要是KELM、SVM方法作为典型基于数据的机器学习方法，用于学习的样本数量要满足一定的数量，较少的训练数据会造成“过拟合”现象.

从识别结果的排名上来看，本文所提方法的识别性能总体上是最优的. 与BRBCS 方法相比能够用较少的模糊划分数量而达到较高的准确识别率. 如在Iris数据集上，本文方法的划分数量为（4，3，4，4），正确识别率为97.33%；而BRBCS 方法当所用的模糊划分为（7，7，7，7）时的正确识别率为96.67%. 降低模糊划分数量带来的优势为：一是增强系统的可解释性，二是生成的规则数量降低，进而能够降低系统运行的时间，提高系统分类性能的实时性. 在其他4 种数据集上，本文方法同样是在较少的模糊划分上获得了较高的识别结果.与SVM、KELM 用于大样本的分类方法相比，本文方法在处理小样本数据识别问题上具有较好的优势.

4 结论

本文提出了参数自适应的析取云模糊置信规则识别方法. 通过两种双门限检测方法，能够有效快速地确定模糊域划分的优化组合方式. 调整云模型的熵和超熵系数，可以改变模糊集的形状. 引入可能度，有效处理冲突条件下置信结果的基本概率赋值问题，并根据优化模型，实现对规则权重和属性权重的优化. 最后，用仿真数据集和实测数据集对所提方法进行验证. 结果表明，设置较少的模糊划分就可获得较高的识别率，能够有效处理小样本识别率低的问题，同时规则的可解释性得到了改善.