弹性配电系统动态负荷恢复的深度强化学习方法

黄玉雄，李更丰，张理寅，别朝红

（西安交通大学电气工程学院,陕西省 西安市 710049）

0 引言

自然灾害、人为攻击和严重技术故障等极端事件严重威胁着电力系统的安全可靠运行［1］。面向极端事件的电力系统弹性研究已越来越受到重视。电力系统弹性是指电力系统承受和抵御极端事件的能力,包括事前预防、事中适应和事后恢复3 个主要阶段［2］。随着碳中和的逐步推进,未来配电系统将接入大量分布式电源（distributed generator,DG）,而微网作为配电系统承载DG 的重要形式,其相应技术将得到大力发展。当极端事件导致主网故障而出现供电能力不足时,配电系统可以通过操作分段开关实现分区,各分区内基于微网盈余电力可为配电系统用户提供电力服务。

近年来,配电系统的弹性评估及提升已成为研究热点。文献［3］分析了能源转型下的弹性电力系统的内涵和前景。文献［4］提出了配电系统弹性的核心特征与关键技术。文献［5-6］提出了电力系统弹性评估与提升的通用研究框架。文献［7-9］研究了极端天气下电网的脆弱性建模方法与恢复措施。文献［10］对主动配电系统的弹性研究现状进行了系统性的综述。对于极端事件,相比于事前的设备强化投资,事后或事中的高效负荷恢复被认为是更加经济可行的电网弹性提升方案。文献［11］较早提出了考虑微网参与的配电系统事后运行模式,将弹性配电系统的关键负荷恢复问题建模为混合整数线性规划问题。文献［12］提出了多源协同的配电系统多时段负荷恢复优化决策方法。此外,现有研究还考虑了微网频率稳定性［13］、配电网络拓扑重构［14-15］、配电系统线性拓扑约束［16］、储能设备与需求侧管理［17-18］、分层故障管理［19］、可再生DG 出力不确定性［20］等因素对含微网的配电系统负荷恢复的影响。

目前,大多数的关键负荷恢复研究是将恢复问题建模为数学规划模型,进而基于最优化理论求解。这类基于模型的方法存下以下问题:1）需要建立研究对象的显式数学模型,这对于复杂系统而言存在很大难度；2）最优化理论中对于可解性的要求使得模型中存在不同程度的简化；3）当在线应用时,优化问题的高效求解仍然面临着挑战。针对上述问题,无模型的机器学习方法被认为是一种可能的解决途径［21］。

本文基于无模型的深度强化学习（deep reinforcement learning,DRL）技术,研究含微网的弹性配电系统在失去主网供电能力情况下的事后动态关键负荷恢复（dynamic critical load restoration,DCLR）问题。这里的“动态”取自动态规划［22］的概念,有别于电力系统动态特性。相较于传统的静态关键负荷恢复模型,本文将恢复问题建模为马尔可夫决策过程（Markov decision process,MDP）,恢复过程被拆分为一系列单阶段问题逐次求解,各阶段决策考虑了未来一定步数决策的影响,各阶段的解组成全过程最优的决策序列。具体而言,首先分析考虑微网的DCLR 问题,并在此基础上建立相应的MDP 模型,同时构建基于OpenDSS［23］的DCLR 模拟环境,形成“智能体-环境”交互接口（agentenvironment interface,AEI）。然后,采用深度Q 网络（deep Q-network,DQN）［24-25］算法寻求最优控制策略,并定义评价指标用于定量评估智能体在训练和应用环节的表现。最后,基于改进的IEEE 测试系统进行算例分析,以验证所提方法的有效性。

1 问题建模

首先,介绍MDP 的基本概念与DCLR 的数学模型,在此基础上,通过定义状态空间、动作空间等MDP 要素,建立DCLR 问题的MDP 模型。最后,基于OpenDSS 建立DCLR 模拟环境,形成DRL 应用所需的智能体-环境交互接口。

1.1 MDP 基本概念

MDP 从智能体和环境的互动中学习控制策略,以实现控制目标,是序贯决策的经典表现形式,其由五元组{S,A,P,r,γ}表示,其中S为状态空间；A为动作空间；P(s′|s,a)为在采取动作a后由状态s到达状态s′的概率；r(s,a,s′)为在采取动作a后由状态s到达状态s′的立即奖励；γ为折扣因子,0 ≤γ≤1。

在智能体与环境的交互中,首先,在时刻t,智能体基于环境的状态st(∈S）选择动作at(∈A)；然后,环境根据概率P(st+1|st,at)转移到状态st+1,智能体获得立即奖励rt=r(st,at,st+1)。智能体在交互过程中通过学习获得决策能力,决策目标是最大化其处于给定状态s或状态-动作对(s,t)时的价值,这一价值可由累计奖励的期望进行估计。动作价值函数Qπ(s,a)的数学表达式为:

式中:π为控制策略,表示状态与选择每个可能动作概率的映射；Eτ～π(·)为状态s从采取动作a开始遵循策略π所获得的期望折扣回报函数；τ为MDP 轨迹；RTτ为从时刻t开始到时刻T结束的MDP 片段（episode）的折扣回报。

γ用于描述预期的未来奖励对当前决策的影响,γ越接近0,表明智能体的目标越“近视”（即向前考虑的步数越少）,智能体的训练难度越小,反之,若γ越接近1,则智能体向前考虑的步数越多,智能体的训练难度越大。

1.2 动态关键负荷恢复

极端事件下,配电系统可能在一段时期内无法通过变电站或馈线获取主网电力,在此期间,配电系统运营商（distribution system operator,DSO）可以基于分段开关和DG 将配电系统分解成多个孤岛微网,从而为关键负荷继续供电,并提升电网弹性［26］。

DCLR 的动态决策过程如图1 所示。其中,恢复时间被离散化,记为集合Γ,|Γ| =T。DSO 在各时间点t∈Γ均会进行负荷恢复决策,且DSO 的每次决策受到当前和未来奖励的影响。

图1 DCLR 问题的动态决策示意图Fig.1 Schematic diagram of dynamic decision-making for DCLR problem

将配电系统记为图G=(N,L),其中N和L分别表示节点集合和线路集合。微网所在节点的集合记为M⊂N。分段开关以集合W表示,每个节点i(∈N)的有功功率和无功功率分别记为pt,i,φ和qt,i,φ,其中φ∈{a,b,c}表示相别；ωi表示节点i负荷的权重系数。以下将从恢复目标和约束条件2 个方面进一步分析DCLR 问题的数学模型,以此作为后续建立DCLR 的MDP 以及AEI 的基础。

1.2.1 恢复目标

DCLR 的目标为在恢复期间的加权负荷恢复总量的数学期望最大,可表示为:

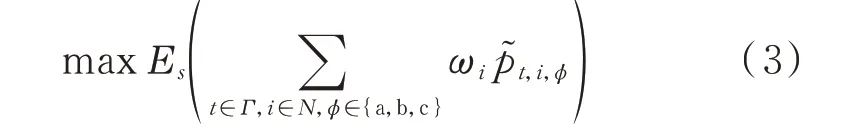
式中:Es(·)为考虑了系统状态s中随机扰动后的数学期望函数；p～t,i,φ为实际恢复负荷,p～t,i,φ=vt,i,φ pt,i,φ,其中,vt,i,φ为二值状态变量,用于表示负荷pt,i,φ的恢复状态,vt,i,φ=1 表示已被恢复,vt,i,φ=0 表示未被恢复,当微网供电范围确定时,vt,i,φ也随之确定。

1.2.2 约束条件

本文在DCLR 问题中考虑3 类约束,分别为配电系统运行约束、微网运行约束以及用户满意度约束。

1）配电系统运行约束

配电系统负荷恢复应满足三相不平衡潮流方程:

式中:It,l,φ为时刻t线路l相别φ的电流幅值；Il,min和Il,max分别为线路l电流幅值的下限和上限。

2）微网运行约束

在配电系统失去主网供电后,微网处于孤岛运行模式,微网中的DGs 不仅可以作为备用机组向本地负荷供电,而且可以通过操作分段开关或微网开关为微网之外的配电系统负荷提供电力服务。假设微网中的DGs 采用主从控制策略［27］,其中系统的电压和频率仅由一个DG（即主机）控制,其余DGs（作为从机）工作在电流控制模式下。因此,当配电系统被分解成多个孤立的微网时,各配电系统分区应满足辐射状网络拓扑约束,即每个关键负荷仅由1 个微网通过1 条路径供电,任意2 个微网之间不存在路径（本文不考虑电网簇［28］）。实际上,保持辐射状的网络结构有助于简化许多运行问题,例如微网之间的同步和负荷分配问题。此外,辐射状网络使得继电保护装置更加容易整定,系统可以免受潜在的后续故障的影响。因此,微网h∈M可由图gh=(NM,h,LM,h)表示,gh∈G且对于∀微网h1∈M,∀微网h2∈M,h1≠h2,gh1⋃gh2=∅。需要注意,这里的微网h泛指由微网h供电的配电系统分区。其中,NM,h和LM,h分别为微网h的节点集合和线路集合。

本文从DSO 的视角来考虑DCLR 问题,将微网视为一个整体,微网与配电系统之间的交互体现为公共连接点（point of common coupling,PCC）的功率传输［11,29］。时刻t微网h输出的有功功率和无功功率pt,h和qt,h需要满足微网容量约束和爬坡速率约束:

式中:pt,h,max和pt,h,min分别为时刻t微网h的有功功率上限和下限；qt,h,max和qt,h,min分别为时刻t微网h的无功功率上限和下限；ph,max和ph,min分别为微网h的有功功率、无功功率上限和下限；qh,max和qh,min分别为微网h的无功功率上限和下限；δh,p和δh,q分别为微网h的有功功率和无功功率爬坡速率,δh,p∈(0,1],δh,q∈(0,1]。

3）用户满意度约束

用户满意度约束常见于电力系统可靠性研究［30-31］。从用户断电次数、用户断电电量等方面描述用户对于电力公司所提供电能服务的满意程度。本文在DCLR 问题中考虑用户满意度对恢复决策的影响,假设在事后恢复期间,当2 处负荷的重要程度（即加权负荷大小）相近时,DSO 不会通过中断一处负荷的方式来恢复另一处负荷,即DSO 会尽可能在维持已恢复负荷的基础上再考虑恢复其他负荷。假设用户满意度约束满足马尔可夫性质,即若给定当前状态,则未来状态与过去状态之间相互独立,该性质表述为:

根据这一假设,且考虑到负荷重要程度对于恢复决策的影响已在恢复目标式（3）中体现,因此,DCLR 中的用户满意度约束可通过对断开当前处于闭合状态的开关这一动作进行惩罚的方式来体现。

1.3 动态关键负荷恢复的MDP 模型

针对DCLR 数学模型,通过定义智能体、交互环境、控制动作、系统状态和奖励函数等要素来构建DCLR 的MDP 模型。

1）智能体和交互环境

DCLR 问题中的智能体将承担DSO 的角色,从配电系统的全局角度制定负荷恢复策略。与智能体交互的环境为具备动作执行、状态分析和奖励反馈等功能的配电系统模拟器。

2）控制动作

智能体在时刻t所采取的控制动作表述为:

式中:ot,w为二值状态变量,表示时刻t针对开关w的操作,ot,w=0 表示闭合操作,ot,w=1 表示断开操作。由于动作空间A由有限的二值状态变量组成,因此,A具有“离散”的特点。

3）系统状态

在时刻t,系统状态由3 类与DCLR 决策主要相关的参数构成,即配电系统负荷参数（基于配电系统运行约束选取）、微网有功功率和无功功率上下限约束（基于微网运行约束选取）以及开关状态参数（基于用户满意度约束选取）。系统状态表述为:

由于状态空间S中包含功率类的连续变量,因此,S具有“连续”的特点。此外,st仅由部分可观参数构成,而其他参数（例如节点电压、线路电流）对决策的影响,可以假设智能体能够在与环境的交互过程中主动学习得到。

4）奖励函数

奖励函数直接影响智能体的决策行为,因此,奖励函数的设计需要综合考虑恢复目标和约束条件对于决策的影响。本文将约束条件分为2 类:硬约束和软约束,如表1 所示。恢复期间,若智能体决策违反软约束,则智能体将受到惩罚（即负值奖励）,而负荷恢复可以继续进行；若违反硬约束,则智能体将受到严重惩罚,且负荷恢复失败。

表1 约束条件的类别Table 1 Categories of constraint violations

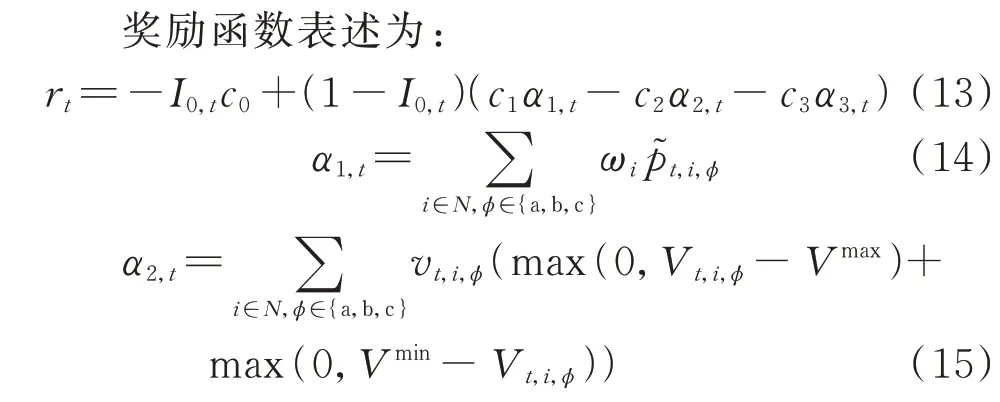
在式（13）中,-c0表示违反硬约束的惩罚；c1α1,t表示恢复负荷的奖励；-c2α2,t表示违反节点电压约束的惩罚；-c3α3,t表示违反用户满意度约束的惩罚。 本文取c0=100,c1=0.004 kW-1,c2=0.1,c3=0.1。在这一系数设置下,对于用户满意度约束而言,2 处负荷的重要程度相近可以理解为2 处负荷的有功功率在加权后的差距在25 kW 以内（25 kW约为节点13 与节点37 系统中最小的单相负荷）。

1.4 基于OpenDSS 的AEI 实现

与智能体交互的DCLR 模拟环境具备2 个基本功能,即三相不平衡潮流计算和拓扑分析。其中,拓扑分析用于校验辐射状网络拓扑约束；三相不平衡潮流计算用于校验其他约束。st和rt中的参数通过读取潮流计算结果的方式得到。

本文基于Python 和OpenDSS 构建确定性的DCLR 模拟环境,进一步形成AEI。 首先,在OpenDSS 中搭建测试系统的三相不平衡潮流计算模型。其中,将微网建模为恒压源并连接至配电系统相应节点。此外,将配电系统的网络拓扑以图数据的格式进行存储,基于此,针对智能体做出的决策,利用深度优先搜索算法［32］校验拓扑约束。然后,通过OpenDSS 组件接口,实现基于Python 的DCLR 模拟。在拓扑分析和潮流计算完成后,基于式（12）—式（16）形成系统状态和奖励并反馈给智能体。

DCLR 的智能体-环境交互框架如图2 所示。训练环节得到的智能体可以保存并用于应用环节,这一“离线训练-在线应用”的模式可以充分发挥神经网络输入输出映射的速度优势,从而有效提升应用环节的计算效率。

图2 负荷恢复问题的智能体-环境交互框架Fig.2 Agent-environment interaction framework of load restoration problem

2 算法实现

强化学习是求解MDP 的一般性框架。在所建立DCLR 的MDP 模型中,最优负荷恢复策略可表达为价值最高的控制动作。针对DCLR 问题“状态空间连续-动作空间离散”的特点,采用DQN 算法,通过值迭代的方式来搜索价值最高的控制动作。DQN 作为一种无模型的深度强化学习算法,在搜索最优策略的过程中无需额外的先验知识。

2.1 DQN 原理

根据贝尔曼最优性［17］,上述迭代过程最终将收敛至最优价值函数,即Qμ(s,a)→Q*(s,a),i→∞。由于难以单独估计每个状态-动作对的动作价值,因此,一般使用函数逼近的方法来估计动作价值函数。Q 网络指具有权值参数θ的神经网络函数逼近器,可表示为Q(s,a；θ)≈Q*(s,a)。

针对损失函数F(θμ),可基于随机梯度下降法等优化算法对参数θ进行迭代更新。

Q 网络采用多层感知机模型,输入为系统状态,输出为各动作的动作价值,输出中最高动作价值对应的动作即为最优负荷恢复策略。

2.2 Q 网络训练算法

DQN 训练算法步骤如下:

步骤1:初始化经验回放池、动作价值网络Q 以及目标动作价值网络Q^ ,episode 取1。

步骤2:初始化环境状态st,t=0。

步骤3:基于ε-贪婪策略选择动作at。

步骤4:在DCLR 环境中执行at,环境反馈奖励rt和下一状态st+1,将经验(st,at,rt,st+1)存入经验回放池。

步骤5:从经验回放池中随机抽取小批量样本ηt。

式中:ε0和ε∞分别为初始和最终的探索率；tε为状态转移步数；cε为探索率衰减系数。

为保证算法的收敛性,DQN 使用了经验回放和目标网络2 个技巧,相关内容可参考文献［24-25］。

2.3 评价指标

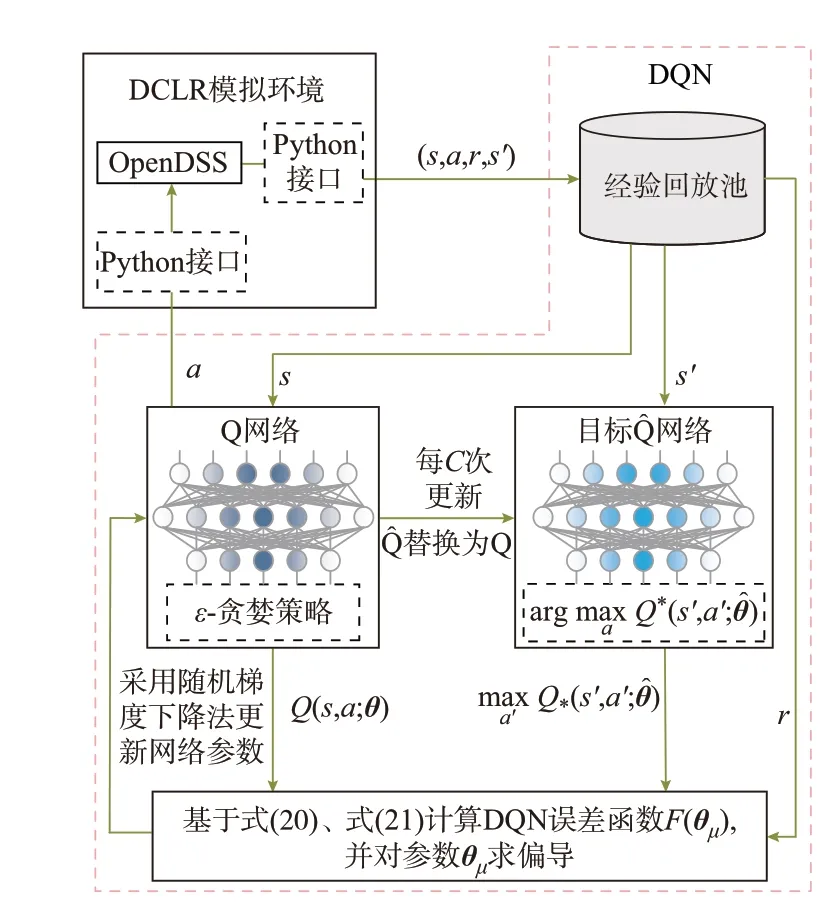
图3 DQN 训练算法原理图Fig.3 Schematic diagram of DQN training algorithm

智能体的收敛性指标和决策能力评价指标分别用于定量评价智能体在训练环节和应用环节的表现。收敛性指标包括:平均片段得分（average score per episode,ASPE）［28］、平均动作价值（average action value,AAV）［28］和平均批次损失（average loss per batch,ALPB）。决策能力指标包括:平均成功率（average success rate,ASR）和平均最优性差距（average optimality gap,AOG）。

ASPE 表示一个训练周期（epoch）内每个片段的平均折扣回报；AAV 表示在一个训练周期内所选动作的平均价值；ALPB 表示在一个训练周期内每个训练批次的平均训练损失。计算公式分别为:

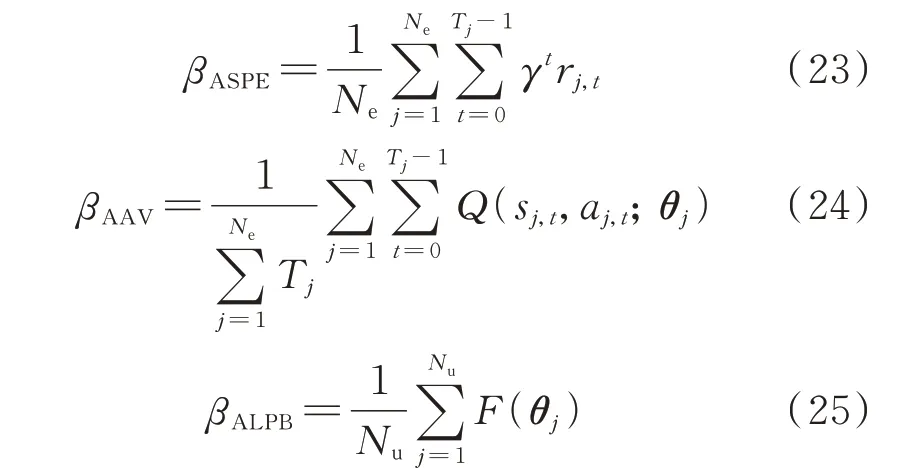
式中:Ne为训练周期内的片段数目；Tj为片段j的长度；Nu为1 个训练周期包含的参数更新次数；sj,t、aj,t、rj,t、θj分别为片段j的状态、动作、立即奖励和参数。

针对应用环节,考虑到DRL 具有黑箱问题,本文从动作的可行性和最优性2 个方面来衡量智能体的决策能力。在决策能力指标中,ASR 表示智能体采取可行动作的概率,ASR在[0,1]范围内取值,ASR 越趋近于1,表明智能体越为可靠；AOG 衡量基于DRL 的决策解和基准解在恢复目标方面的差距,AOG 越接近于0,表明所提方案与基准方案在最优性方面越接近。

对于ASR 指标,调用Q 网络生成多个具有长度上限的决策片段,长度上限用于避免生成过长的片段,因此,ASR 定义为生成片段中可行动作的占比:

式中:Rj为辨识片段j是否以不可行动作结束的变量,Rj=1 表示是,Rj=0 表示否。

对于AOG 指标,调用Q 网络生成多个固定长度的决策片段,片段中均不含不可行动作。对于每个片段,基于DRL 的决策方案和基准方案之间的最优性差距βgap表示为:

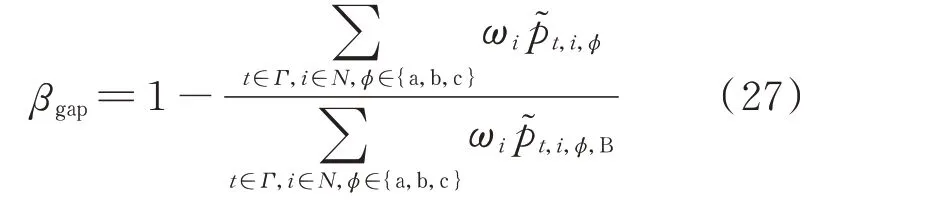
式中:p～t,i,φ,B为基准方案中实际恢复的负荷。AOG指标则为生成片段的平均最优性差距。

3 算例分析

将所提方法应用于2 个改进的IEEE 测试系统,即IEEE 13 节点馈线系统（本文简称13 节点系统）［33］和IEEE 37 节点馈线系统（本文简称37 节点系统）［34］,以验证其有效性。所有计算均在搭载Intel Core i7-8700 3.20 GHz CPU,8 GB RAM的计算机上进行。所提方案与基准方案2 的环境配置为Python 3.6.12、PyTorch 1.8.0 和OpenDSS 9.1.0.1；基准方案1 的环境配置为MATLAB 和Gurobi 9.1.0。本项工作未使用GPU 加速计算和分布式训练。

3.1 测试系统

13 节点系统中设置了2 个微网,分别接在节点633 和692；同时设置了4 个分段开关用于执行负荷恢复决策,分别安装在线路632-645、670-671、671-684 和671-692。37 节点系统中设置了4 个微网和6 个用于执行负荷恢复决策的分段开关。13 节点与37 节点系统的三相拓扑见附录A。此外,假设下一时刻的负荷在当前负荷的基础上加上±30%的随机波动,微网的爬坡速率为100%。测试系统的具体数据,例如负荷参数、微网参数、状态空间、动作空间的设置等分别见附录B 和C。

3.2 训练效果

训练环节首先需要确定各测试系统所对应的Q网络的架构。经过尝试,最终确定Q 网络由4 个全连接线性层组成,每个线性层后均接有修正线性单元（rectified linear unit,ReLU）。输入层的神经元数目等于状态s中的参数数目（13 节点系统的输入层神经元数量为42；37 节点系统的输入层神经元数量为82）。两个隐藏层均包括512 个神经元。输出层的神经元数目等于动作空间A中动作的数目（13 节点系统的输出层神经元数目为16；37 节点系统输出层神经元数目为30）。然后,基于DQN 算法训练Q网络,训练环节中的超参数取值见附录D。此外,本文中所使用的随机梯度下降算法为Adam［35］。

基于附录B 和C 中测试系统参数设置和附录D中超参数设置,针对折扣因子γ的取值,设置如表2所示的3 个测试场景,用于分析DCLR 问题中智能体“近视”程度对于训练和应用效果的影响。

表2 测试场景设置Table 2 Setup of test scenarios

图4 展示了训练过程中收敛性指标的变化情况。其中,ASPE 的变化趋势可基于片段长度和立即奖励大小来分析。

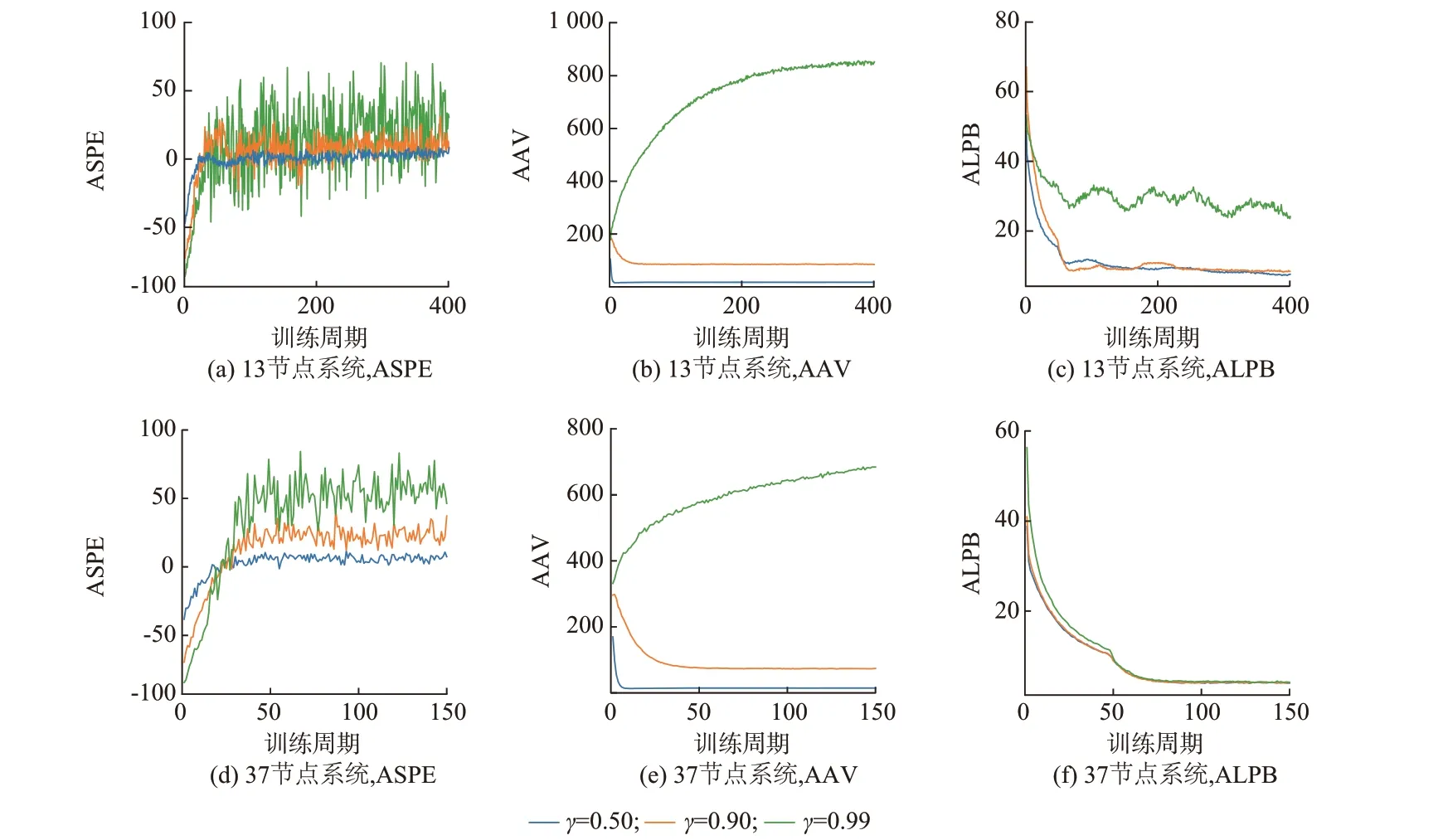
图4 ASPE、AAV、ALPB 训练曲线Fig.4 Training curves of ASPE, AAV, and ALPB

ASPE 前期收敛较快表示智能体经过较少训练周期就能学习到可行控制策略。此后,智能体会采取一些回报更高但失败风险也更大的动作以提升立即奖励,这可能使得恢复片段提前终止,并伴随负值奖励作为惩罚。因此,后期当风险与收益没有得到很好的权衡时,ASPE 曲线会出现明显波动。为避免训练发散,可在优化算法中适当选取较小的学习率（见附录D 表D1）。此外,当γ取值越小时,由于智能体越为“近视”,因此,片段长度会更短,ASPE的收敛值也更小,如图4 所示。需要说明的是,DQN 算法对回放池中负样本（即违反硬约束的经验）的比例比较敏感,而ASPE 较小意味着负样本比例会相应地变大,所以本文中的折扣因子取值不宜过小。

对于AAV,通过监测训练过程中Q 网络的输出发现,所有动作的价值随时间变化的趋势分为2 类:一类会很快收敛至0,这对应于不可行动作（即违反硬约束的动作）；另一类对应于可行动作,其价值逐渐收敛至期望折扣回报,且所有可行动作具有相似的变化趋势。这解释了AAV 变化趋势的平稳特征。对于场景1 和2,γ取值较小,使得期望折扣回报较小,且低于Q 网络初始值,AAV 呈现下降趋势；而场景3 中期望折扣回报高于Q 网络初始值,AAV呈现上升趋势。此外,对于ALPB,该指标与Q 网络损失直接相关,可较为直观地体现智能体的训练难度。

此外,虽然13 节点系统的输入与输出参数的数目少于37 节点系统,但由于其动作空间包含了所有可能的开关动作组合（见附录B）,而37 节点系统的动作空间中已提前删去了违反拓扑约束的34 个开关动作组合（见附录C）,使得13 节点系统的动作空间中存在较多不可行动作（在基础负荷下,13 节点系统动作空间中不可行动作占比为1/2；37 节点系统为2/5）；另一方面,相比于37 节点系统,13 节点系统中的关键负荷总量与微网容量较为接近（见附录B 和C）。因此,在类似的训练环节下,37 节点系统的“学习难度”反而小于13 节点系统,其训练效果也更优,如图4 所示。

训练结果表明13 节点和37 节点测试系统的智能体均可以取得较好的收敛结果,且收敛性指标在训练初期的收敛速度较快。针对同一系统的不同测试场景,γ取值越小,则训练环节的收敛效果越好。这与1.2 节的分析一致,即γ越小表示智能体在决策时向前考虑的步数越少、训练难度越小。此外,ASPE 和ALPB 的收敛特性较为相似,AAV 的变化趋势更为平滑。在计算效率方面,对于13 节点系统,训练一个训练周期数目为500 的智能体需要5 h左右；对于37 节点系统,训练一个训练周期数目为150 的智能体需要2 h 左右。

3.3 应用效果

在应用环节中,将系统状态输入训练好的Q 网络,并选择输出中最高动作价值对应的动作作为每次负荷恢复决策的最优解。本文将所提方案与3 个基准方案进行对比来分析其在决策最优性和计算效率方面的表现。基准方案1 为文献［29］所提的基于模型的求解方法,其中DCLR 问题被建模为混合整数线性规划（mixed-integer linear programming,MILP）问题。基准方案2 和3 将DCLR 问题视为各时间段的单阶段静态关键负荷恢复问题的直接组合。每个单阶段静态关键负荷恢复问题通过在OpenDSS 中遍历动作空间,并将其中恢复关键（加权）负荷最多的动作视为最优解。所提方案与基准方案之间的主要区别如表3 所示。决策能力指标结果如表4 所示,可以发现γ取值较大时ASR 和AOG指标更优,这意味着DCLR 问题中γ较大时智能体的决策能力更优。

表3 恢复方案之间的区别Table 3 Differences between restoration methods

表4 应用环节的指标结果Table 4 Index results of application segment

对于ASR,场景3 下13 节点系统与37 节点系统的智能体分别达到99.99%和99.98%。实际应用中为保证系统的安全运行,需要对基于DRL 的决策解进行安全校验。本文设定如下校验机制:当最优解违反硬约束时,选择次优解（即Q 网络输出中第二高动作价值所对应的动作）,并对其进行校验。该校验过程可以重复直到校验通过为止。实验发现,在仅设置一轮安全校验的情况下（即只对最优解进行校验）,场景3 下2 个测试系统的ASR 指标普遍达到100%。

对于AOG,所提方案与基准方案的结果较为接近。实验发现,相同恢复策略下,基准方案2 的潮流计算结果中,部分节点的负荷略低于基准方案1 中所得到的结果,即潮流模型的差异（见表3）使得AOG1 大于AOG2。为进一步分析误差来源,针对13 节点系统和场景3,选择了一组分别由所提方案和基准方案得到的决策片段,如附录E 图E1 所示,并从每次状态转换的立即奖励和恢复负荷2 个方面分析最优性偏差的来源。对比所提方案和基准方案2,可以发现最优性偏差主要来源于智能体的保守性决策,例如附录E 图E2 中的第84 次和第87 次状态转换；对比所提方案和基准方案3,可以发现考虑到用户满意度约束,智能体会做出一些回报较高但恢复负荷较小的决策,例如附录E 图E2 中的第43 次和第55 次状态转换（附录E 中讨论了第42 次和第43 次状态转换对应的负荷恢复过程）。前者反映了智能体的风险回避特性,需要通过改进训练算法等方式来提升智能体的决策能力；而后者是因为所提方案和基准方案3 在决策目标上具有差异,这体现了智能体在处理复杂问题时的有效性。

应用环节的计算效率对比如表5 和表6 所示,其中计算效率定义为平均单次决策耗时。对于所提方案,借助于Q 网络的输入输出映射关系,其在应用环节极具效率优势,且计算效率随系统规模的变化而降低。由于动作空间离散且动作数目较少,因此,基准方案2 和3（基于枚举）的计算效率与基准方案1 相当,均在秒级左右。

表5 应用环节的计算效率Table 5 Computational efficiency of application segment

表6 应用环节的计算效率比值Table 6 Computational efficiency ratio of application segment

离线训练得到的Q 网络仍然可以根据应用需求来滚动更新其网络参数,以进一步保障基于DRL的决策方案在实际应用中的适用性。

4 结语

本文提出了一种基于DRL 的面向弹性提升的含微网配电系统动态关键负荷恢复方法,可以在极端事件导致主网供电能力不足时为配电系统中的关键负荷恢复提供解决方案。基于智能体-环境交互过程,所提方法支持端到端的决策方式。算例结果表明,基于DRL 的方法可以成功地学习负荷恢复策略,且无需额外的先验知识。在实际应用中,通过引入安全校验,可以有效保证决策的成功率和系统的安全运行。对于决策的最优性,尽管智能体还存在一定的决策保守性,但整体而言,所提方法具有较好的表现。此外,所提方法在应用环节的计算效率方面具有明显优势。

同时,本文工作也存在一定局限性,进一步的研究将处理更为复杂的恢复场景和恢复动作,并尝试量化恢复期间的不确定性因素对恢复结果的影响。此外,还将针对DRL 算法、高性能计算,以及面向DRL 应用的标准化负荷恢复模拟环境及其开源等问题展开研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。