基于高保真度目标函数的直齿圆柱齿轮优化设计

盛文达，李显培，林涛，任宜青，张玮，孙梦

基于高保真度目标函数的直齿圆柱齿轮优化设计

盛文达，李显培，林涛，任宜青，张玮，孙梦

（长安大学 工程机械学院，陕西 西安 710048）

在使用遗传算法对直齿圆柱齿轮进行优化设计计算时，通常采用近似模型替代齿轮模型建立目标函数，但经数次迭代计算后，误差被放大，会影响全局寻优的准确性。本文提出一种建立高保真度目标函数数学模型的方法，用于保证遗传算法全局寻优的准确，不仅考虑腹板、减重孔和轴质量的基础上增加考虑齿轮传动中大小齿轮齿宽不等、齿轮轴长度、顶隙、键槽等因素，还引入齿顶高、齿根高、键槽长宽、修正系数等参数。在设计材料数据相同条件下，相比传统优化设计，使用本文提出的高保真度目标函数进行遗传算法优化计算得出的优化结论在重量上减轻了11.67%，且经过ANSYS分析校核，该优化设计结论模型满足设计要求。

高保真度；优化设计；直齿圆柱齿轮；目标函数

在齿轮的设计过程中，存在着目标函数多、约束条件复杂等特点，因此，齿轮设计在学术研究中备受青睐，推动着齿轮设计生产过程和产品性能的不断优化[1]。

结合运动学、强度设计、计算机技术等，采用迭代方法对齿轮设计参数进行优化设计，在兼顾设计参数的同时，还能缩短设计周期[2]。还有学者通过开发软件、算法优化和增加约束条件等方式求解直齿圆柱齿轮系设计系数的最优组合问题，从而对直齿圆柱齿轮进行优化设计[3-4]；R.C.Sanghvi等[5]利用多目标优化技术（NSGA-II）以面宽、模量和齿数为设计变量对二级斜齿轮传动进行了优化，通过帕累托最优（Pareto Optimality）兼顾体积和负载能力达到双目标最优设计；任建华等[6]利用Matlab优化工具箱进行优化设计，通过选取设计参数、构建目标函数、确定约束条件，验证优化工具箱对于齿轮优化的可行性；陈强等[7]通过Matlab软件对二级斜齿轮减速器进行中心距、总重量、螺旋角的多目标优化设计，通过归一化处理、分配适当的权值，实现多目标优化设计；Brahim M等[8]提出了基于GA（Genetic Algorithm）和RBF（Radial basis function）的两级优化方法，将齿轮的最优重量进一步优化。

遗传算法是一种全局搜索的优化方法，通过选择、交叉和变异进行优化重组，从而实现全局搜索，得出全局最优解[9-14]。

学者们利用计算机对齿轮进行了优化设计，根据优化设计对象的不同，可分为：一级、二级圆柱齿轮和斜齿轮、圆锥齿轮、齿轮箱、齿轮系、减速器等[15-29]。

同类型齿轮的应用场所不同，则优化设计时所选目标函数也不尽相同。近年来，由于高性能动力传输（如汽车、航空航天等）的广泛应用，齿轮传动的最小重量设计问题成为了研究热题，在材料不变的前提下转化为体积优化问题，最终体现在目标函数的建立上，目标函数模型对于齿轮物理模型的保真度，决定了优化结论的准确性。传统优化设计往往采用近似模型替代齿轮模型建立目标函数，通过迭代计算后误差被放大，最终影响优化结论。为了使优化结论数据与物理测试数据达到相当的精度水平，数学模型也应尽可能地接近真实物理模型。因此本文对比传统优化设计，建立直齿圆柱齿轮重量优化的高保真度目标函数，通过Matlab遗传算法进行迭代优化计算，得出优化设计结论。

1 直齿圆柱齿轮及传统优化设计

直齿圆柱齿轮是工业上广泛应用的功率传递机械装置，其啮合如图1所示，其中：腹板减重孔数量＝6，0≈1.62，I＝2.5（为模数），3＝2－2I－2h（h为齿根高系数），2＝1（为传动比），b＝3.5，d＝0.25(3－0)，1＝1。

b1、b2为小齿轮、大齿轮齿宽，mm；bw为腹板厚度，mm；d0为大齿轮轮毂直径，mm；d1、d2为小齿轮轴、大齿轮轴直径，mm；Iw为轮缘厚度，mm；D1、D2为小齿轮、大齿轮分度圆直径，mm；D3为大齿轮边缘内径，mm；dp为减重孔直径，mm。

传统优化设计在建立目标函数时，选取模数（按标准模数系列选取）、小齿轮齿数1（整数型）、小齿轮齿宽1（浮点型）、小齿轮分度圆直径1、大齿轮分度圆直径2五个参数作为设计计算变量参数。目标函数的建立主要分为两大类：第一类是以分度圆为底、齿宽为高的圆柱体模型建立目标函数，第二类则考虑大齿轮腹板和减重孔而建立的目标函数。

Yokota等[14]建立的齿轮重量目标函数表达式如式（1）所示；Brahim M等[8]建立的齿轮重量目标函数表达式为如式（2）所示。

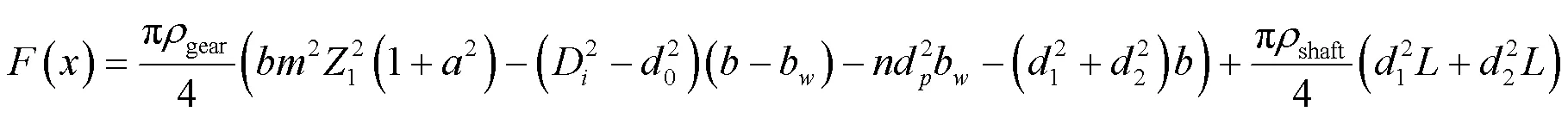
式中：为齿轮密度，g/cm3；为齿宽，mm；为传动比；D为轮毂内径，mm；0、1分别为凸台外径、凸台长度，mm；gear、shaft分别为齿轮、轴密度，g/cm3；为大、小齿轮轴的轴长，mm。

式（1）、式（2）中目标函数数学模型的建立为第二种类型，虽然优于第一类，如张少军[30]以大小齿轮分度圆柱体积之和为目标函数的数学模型，但存在以下问题：

（1）大小齿轮齿宽统一取值为，未考虑实际情况中为保证装配精度、防止齿轮传动中扭矩的传递能力降低，可能发生的齿轮接触面积减小、齿轮磨损不均匀、齿轮发生异响等状况。通常选取小齿轮齿宽1比大齿轮齿宽2多5～10 mm，即1＝2＋（5～10） mm。

（2）未考虑由于齿顶高系数与齿根高系数取值不同而导致的顶隙存在，与实际情况不符。可将顶隙所占重量引入目标函数中，增大目标函数的精确度。

（3）未考虑齿轮与轴连接处键槽的存在。通过引入齿轮轮毂处键槽的重量，也能增加目标函数数学模型的精度。

（4）大小齿轮的轴长统一取值为，与实际设计情况不符。齿轮轴大多为阶梯轴，其轴长的取值是由装配齿轮的齿宽决定的，在齿轮的设计过程中属于未知参数，不影响齿轮的设计计算，因此不应考虑该齿轮轴段重量。

2 高保真度目标函数的建立

本文建立了一种对于齿轮物理模型具有高保真度的目标函数数学模型，用于保证目标函数的保真度对于迭代遗传算法全局寻优的准确性。在目标函数数学模型构建中考虑到齿轮啮合传动过程中大小齿轮齿宽不同、顶隙、键槽等因素，引入齿顶高、齿根高、键槽长宽、腹板减重孔、修正系数等参数进行构建。

结合传统目标函数及其新增因素，建立高保真度目标函数数学模型如式（3）所示：

式中：1、2分别为小齿轮、大齿轮的齿宽，mm，其中1＝2＋5 mm；1、2分别为小齿轮、大齿轮的齿数。

以重量最小为目标函数进行优化设计时须考虑以下条件：

（1）大小齿轮的齿根弯曲强度＜许用弯曲强度，即：

（2）大、小齿轮间的接触应力＜许用接触应力，即：

（3）大、小齿轮轮毂的抗扭强度＜许用扭转切应力，因为大小齿轮轮毂半径不同，因此需要分开计算，即：

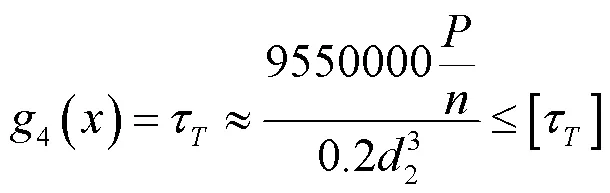
式中：τ、[τ]分别为扭转切应力、许用扭转切应力，MPa；、1分别为齿轮传动功率、小齿轮转速，r/min。

选择齿轮材料17Cr2Ni2Mo，其密度齿轮＝7.8 g/cm3，弹性模量＝210 GPa，泊松比＝0.28，许用弯曲应力σ＝224.16 MPa，许用接触应力σ＝766.77 MPa。

结合齿轮材料和设计参数，查设计手册取K＝1、K＝1、K＝1.0、K＝1.34、Y＝2.65、Y＝1.58、ε＝1.711、K＝1.421、Z＝2.5、Z＝189.8。

3 基于遗传算法的齿轮优化设计方法

遗传算法（Genetic Algorithm，GA）是基于分析模型的低成本计算方法，用一个有限固定长度的二进制字符串表示每一个单独的解决方案（染色体，即直齿圆柱齿轮中1、1、2、1、），然后通过计算适应度值（即目标函数计算值取倒数）来评估每个单独的解（对比适应度值的大小）。

遗传算法结合直齿圆柱齿轮优化计算流程如图2所示。

图2 直齿圆柱齿轮遗传优化计算流程图

遗传算法在每一个亲代生成子代的过程中，遵循自然选择中选择、交叉、变异的规则，能够保留优良组合、产生新的数据、增加子代多样性。本文将交叉率选为0.6、变异率选为0.1进行迭代计算，各参数变量在不断迭代中逐步趋近于最优解，根据Yokota等[14]和Brahim M等[8]使用参数和多次试验结合考虑，在本文中选择初始种群大小为250、迭代次数选择为500。且对变量参数1、1、2、1、限定取值范围为：25≤1≤40、20≤1≤40、20≤2≤40、18≤1≤25、＝（2.5, 2.75, 3, 3.5, 4）。

4 基于高保真度目标函数的齿轮优化计算及强度校核

4.1 优化计算结果

结合文献[8]，本文设置初始设计条件为：传动比＝4，齿轮传递功率＝7500 W，1＝35 mm，1＝23 mm，2＝26 mm，1＝22，＝2.5，轮转动速度1＝1500 r/min，设计中心距＝140 mm。结合本文的目标函数、约束条件和初始设计参数，利用遗传算法进行直齿圆柱齿轮迭代优化计算，得出优化数据结论，如表1所示。通过比较，在同参数条件下，本文优化数据的最优解相较于文献[8]在重量上优化了11.67%。

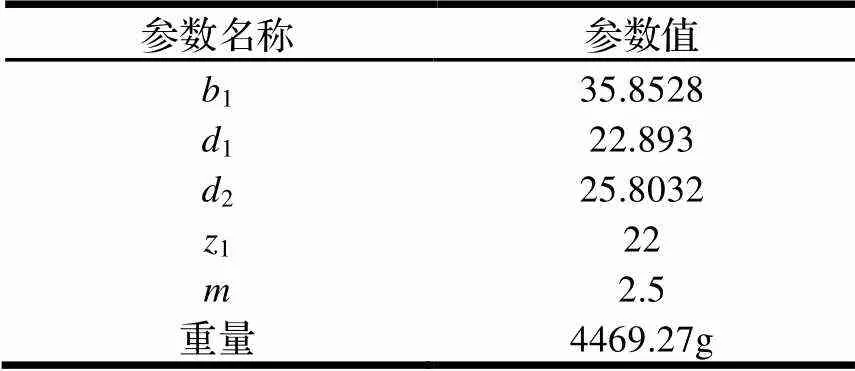
表1 优化结论数据

根据优化结论数据，结合实际加工情况，进行相应的圆整处理，最终得到参数取值为：1＝35 mm，1＝23 mm，2＝26 mm，1＝22，＝2.5。

4.2 强度校核

利用SolidWorks进行三维建模，然后导入ANSYS进行有限元分析，以验证由该方法优化计算得出的齿轮在使用强度上是否满足实际需求。首先用网格划分单元对模型进行网格划分，划分出轮齿啮合单元、轮毂受力单元和腹板部位单元，划分后的模型如图3所示，并对轮齿接触部分做网格细分，以增加轮齿接触部分有限元分析精度和准确度，如图4所示。

图3 齿轮啮合网格划分

图4 轮齿接触部位网格划分

根据设计初始条件及齿轮参数、计算载荷加载进行有限元分析，得出齿轮接触部位和大齿轮轮毂处两个敏感部位受力如图5、图6所示，以及齿轮啮合传动过程变形和轮齿处变形如图7、图8所示。

由ANSYS分析结果可知，由该目标函数进行遗传算法迭代优化设计计算得出的齿轮能够满足承载量需求，且在重载情况下的变形量在可接受范围内，因此该齿轮满足使用需求。

图5 轮齿接触部位von Mises stress

图6 大齿轮轮毂处受力分析

图8 轮齿接触部位变形

5 结论

本文总结前人进行计算机齿轮优化设计计算实例，针对传统目标函数建立过程中由近似模型替代齿轮物理模型的不足，提出一种建立高保真度目标函数的方法。通过对目标函数的改进，使得目标函数的数学模型贴近于实际齿轮啮合传动物理模型，结合计算机优化设计计算迭代寻优的特性，这一方案的优势得以发挥。

对比两个优化结论数据可知，本文通过改进目标函数，即提高目标函数的数学模型对于齿轮啮合传动物理模型的保真度，在遗传算法优胜劣汰的角逐方式下，影响迭代过程中每一个子代的选择，最终得出最优解的设计参数组合。试验证明，改进目标函数对于迭代寻优的影响是存在且明显的，目标函数对于物理模型的保真度能够影响全局寻优的准确性。由实例验证，相同初始设计参数，在满足约束条件和使用条件下，重量相比传统优化计算数据减轻约11.67%。通过利用遗传算法对齿轮啮合传动重量优化设计可知，遗传算法能够很好地应用于多参数的优化问题上，找寻全局最优解。但在使用过程中，最优解的准确度也受目标函数数学模型保真度的影响，因此应注意使用精确的数学模型以提高遗传算法结论的准确性。

[1]冯顺利. 基于神经遗传算法二级斜齿轮参数优化设计[J]. 制造业自动化，2014，36（15）：98-101.

[2]岳桂杰，保承军，董世方. 直齿圆柱齿轮传动的优化设计[J]. 煤炭技术，2012，31（4）：16-17

[3]MARJANOVIC N，ISAILOVIC B，MARJANOVIC V，et al. A practicalapproach to the optimization of gear trains with spurgears[J]. Mechanism and Machine Theory，2018（53）：1-16.

[4]SANGHVI V，RAO R，VAKHARIA D. Optimalweight design of a gear train using particle swarm optimization and simulated annealing algorithms[J]. Mechanism and Machine Theory，2010，45（3）：531-541.

[5]SANGHVI R，VASHI A，PATOLIA H，et al. Multi-objective optimization of two-stage helical gear train using NSGA-II[J]. Journal of Optimization，2014：3-6.

[6]任建华，刘艳层，梁振刚. Matlab在齿轮优化设计中的应用[J]. 机电工程技术，2014，43（11）：76-78.

[7]陈强，王鹏，王斌. 基于遗传算法的二级减速器齿轮优化设计[J]. 汽车实用技术，2019（23）：62-65.

[8]BRAHIM M. Optimum design of a spur gear using a two level optimization approach[J]. Mechanics，2019，25（4）：304-312.

[9]郑则坡，曾佑文，曾刚，等. 基于遗传算法的二级齿轮减速器优化设计[J]. 矿山机械，2010，38（20）：46-49.

[10]谢雄伟，徐宏海，关通. 基于遗传算法的RV减速器零件公差优化设计[J]. 机械传动，2020，44（3）：77-83.

[11]吉巧丽，钱志辉，任雷，等. 基于遗传算法的双足机器人足踝蹬地参数优化[J]. 农业机械学报，2020，51（S1）：584-591.

[12]蒋云彩，万顷波. Matlab遗传算法工具箱（GAOT）的应用[J]. 江西电力职业技术学院学报，2004（3）：42-44

[13]TRUPTI B，OMKAR K，NINAD K，et al. Genetic algorithm and its applications to machanical engineering: a eview[J]. Materials Today: Proceedings，2015，2（4-5）：2627-2629.

[14]YOKOTA T，TAGUCHI T，GEN M. A solution method for optimal weight design problem of 10 bar truss using genetic algorithms[J]. Computers & Industrial Engineering，1998，35（1-2）：369-371.

[15]YOKOTA T，TAGUCHI T，GEN M. A solutionmethod for optimal weight design problem of the gearusing genetic algorithms[J]. Computers & Industrial Engineering，1998，35（3）：523-526.

[16]陈向东. 基于Matlab的齿轮传动系统优化设计[J]. 化学工程与装备，2019（9）：185-187.

[17]单陇红，胡羽沫. 基于Matlab斜齿圆柱齿轮减速器优化设计[J]. 化学工程与装备，2019（8）：227-230.

[18]张志红. 基于Matlab的二级圆柱齿轮减速器优化设计[J]. 内燃机与配件，2018（5）：7-8.

[19]陈步云，黄寅行. 单级圆柱齿轮减速器的优化设计[J]. 机电产品开发与创新，2016，29（4）：62-64.

[20]罗盛，吴涛，曾德惠. 基于Matlab和Solidworks的齿轮优化设计[J]. 煤矿机械，2014，35（3）：23-25.

[21]孙伟，冯江，蒋亦元. 非圆齿轮系大蒜直立移栽机构优化设计与试验[J]. 农业机械学报，2020，51（8）：73-82.

[22]郑红. 基于Matlab的二级斜齿轮减速器优化设计[J]. 煤炭技术，2011，30（8）：24-26.

[23]杜百岗. 基于GA和Solidworks的斜齿轮参数优化与建模[J]. 机械工程师，2011（6）：58-60.

[24]赵运才，任继华，左亮涛. 基于Matlab的齿轮参数优化设计[J]. 有色金属科学与工程，2011，2（1）：96-100.

[25]朱大林，詹腾，张屹，等. 多邻域结构多目标遗传算法[J]. 农业机械学报，2015，46（4）：309-315，324.

[26]申燚. 基于RBF直齿圆锥齿轮遗传算法优化设计[J]. 淮阴工学院学报，2008（1）：24-27.

[27]GOLABI S，FESHARAKO J，YAZDIPOOR M. Gear train optimization based on minimum volume/weight design[J]. Mechanism and Machine Theory，2014：200-209.

[28]YONG Gangli，YONG Meima. Optimal design of gears by means of genetic algorithm and neural network[J]. Applied Mechanics and Materials，2013：817-820

[29]GOLOGLU C，ZEYVELI M. A genetic approach to automate preliminary design of gear drives[J]. Computers & Industrial Engineering，2009，57（3）：1044-1045.

[30]张少军，万中，刘光连. 直齿圆柱齿轮传动设计的全局优化方法[J]. 中南大学学报（自然科学版），2013，44（7）：2736-2743.

Optimal Design of Spur Gear Based on High Fidelity Objective Function

SHENG Wenda，LI Xianpei，LIN Tao，REN Yiqing，ZHANG Wei，SUN Meng

( School of Construction Machinery, Chang'an University, Xi'an710048, China )

When domestic and foreign scholars use genetic algorithm to optimize the design and calculation of spur gear, the approximate model is usually used to replace the gear model to establish the objective function, and after several iterative calculations, the error is magnified, which affects the accuracy of global optimization. Therefore, a mathematical model of high fidelity objective function is proposed in this paper to ensure the accuracy of the global optimization of genetic algorithm. When establishing the mathematical model of objective function, on the basis of the traditional practice that only the web, weight loss hole and shaft mass are concerned, factors such as the difference of tooth width of big and small gears in gear transmission, the length of gear shaft, top clearance and keyway are added into the model. Parameters such as tooth tip height, tooth root height, length and width of keyway and correction coefficient are introduced to construct the high fidelity objective function. With the same initial design parameters and design material data, compared with the traditional optimization design, the optimization conclusion obtained by using the high-fidelity objective function proposed in this paper for genetic algorithm optimization calculation reduces the weight by 11.67%, and the ANSYS analysis and verification shows that the model of the optimization design meets the design requirements.

high fidelity；optimization design；spur gear；objective function

TH132.417

A

10.3969/j.issn.1006-0316.2022.03.008

1006-0316 (2022) 03-0046-07

2021-10-29

盛文达（1995－），男，安徽阜阳人，硕士研究生，主要研究方向为机电液一体化、机械传动控制，E-mail：arlenlxp@163.com。