Caputo型分数阶q-微分方程的初值问题
2022-04-18刘彦芝党云贵
刘彦芝, 杨 艳, 党云贵,2*
(1.吕梁学院数学系, 山西 吕梁 033000;2.湖北大学数学与统计学学院应用数学湖北省重点实验室, 武汉 430062)
近年来,分数阶微分方程因其在物理控制理论、工程学、生物学等各个领域的广泛应用而备受关注.大部分学者所研究的分数阶微分方程侧重于Caputo导数和Riemann-Liouville导数这两个方面[1-8],而对于分数阶q-微分方程的研究相对较少.事实上,在量子物理、光谱分析和动力系统等方面,q-微积分都发挥着极其重要的作用.近年来,q-微积分也愈来愈多地应用于工程学和经济学中.基于此,本文研究如下具有Caputo导数的分数阶q-微分方程初值问题,
(1)

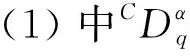
其中,「α⎤为不小于α的最小整数.
众所周知,(1)等价于q-Volterra积分方程[10]
(2)
分数阶微分方程的解在初始点附近具有弱奇异性,这个问题已经成为分数阶微分方程数值分析中主要的关注点[3-8].在方程(1)中也具有类似的弱奇异性,文献[11]详细地讨论了方程(1)解的正则性问题.文献[12]利用q-beta函数给出Caputo型分数阶q-微分方程解的存在性理论并提出循环方法解决此类问题.文献[10]提出了分数阶q-微分方程的一种新的解法并研究其收敛性,且在截断误差的分析中要求方程的解在整个闭区间上足够光滑.本文则讨论当方程的解不够光滑时相应数值方法的误差估计.参考关于非线性分数阶常微分方程解的正则性常用的一些假定[6,11],提出
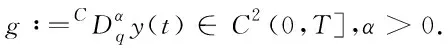
|g'(t)|≤Ctα-1, |g″(t)|≤Ctα-2.
(3)
1 预备知识
本节主要介绍q-微积分的相关定义及引理,且文中出现的q均为同一个数.
定义1[13]对任意t,s∈,(t-s)υ的q-模拟幂为
定义2[13]q-Γ函数定义如下:
Γq(δ)=(1-q)1-δ(1-q)(δ-1),
这里(1-q)(δ-1)指的是(1-q)1-δ的q-模拟幂.
定义3[13]函数g在[0,t]上的q-积分和q-导数分别定义如下:
定义4[13]设g为定义在[0,+∞)上的函数,g的δ阶Riemann-Liouville型q-积分定义如下:
引理1[11]设α∈(0,1)∪(1,2),0≤s≤t≤1,则有

2 主要结论
本节将通过逼近方程(2)右端的积分项,得出求解方程(2)的预估-校正格式并进行详细的误差估计.
2.1 基于变步长的预估-校正格式
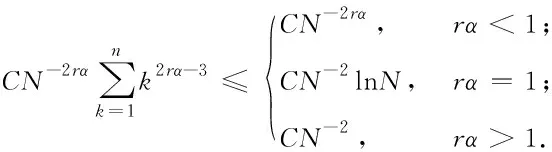
令0=t0 (4) 步长τk=tk-tk-1,易得 τk≤rTN-rkr-1. (5) 为方便起见,在计算中不妨假定T=1. 由(2)得到在点t=tn,n=0,1,…,N-1,有 (6) 在(6)式中,用P0(s)逼近等式右端项f(s,y(s)),可得 其中, P0(s)=f(tk-1,y(tk-1)),s∈[tk-1,tk], k=1,2,…,n. 在(6)式中,用P1(s)逼近f(s,y(s)),可得 其中, k=1,2,…,n, Bk=tkAk(tkqm-tk-1)- tk-1Ak-1(tk-1qm-tk-1), Ck=tk+1Ak+1(tk+1qm-tk+1)-tkAk(tkqm-tk+1), k=1,2,…,n-1. 设yj≈y(tj),其中j=0,1,…,n.定义如下预估-校正格式: (7) 1) 若0<α<1,有 2) 若1<α<2,有 I1≤CN-2. 证明由于 由假定1可得 注意到 |an,n|≤ Cnr(α-1)N-r(α-1)N-rnr-1=Cnrα-1N-rα, (8) 结合引理1、引理2,有 从而 I1≤ 若0<α<1,有 若1<α<2,注意到r(α+1)-2>-1,有 1) 若0<α<1,有 2) 若1<α<2,有 |y(tn)-yn|≤CN-2. 证明 对于I1,存在ξk∈(tk-1,tk),k=1,2,…,n,满足 由假定1、引理1、引理2及(5)式,得 若0<α<1,有 (9) 若1<α<2,注意到r(α+1)-2>-1,则有 (10) 对于I2,由注2得 对于I3, 因此, (11) 下面用数学归纳法证明.首先考虑0<α<1的情形,此时,再分三种情形来讨论. Case1rα>1. 假设存在常数C0>0满足 |y(tj)-yj|≤C0N-2, j=0,1,2,…,n-1;n=1,2,…,N, 下证 |y(tn)-yn|≤C0N-2. 事实上,由式(8)、(9)、引理3、注1及注2可得 |y(tn)-yn|≤CN-2+ CN-2+CC0TαN-2+CN-2+TαN-1C0N-2. (12) Case2rα<1. 假设存在常数C0>0满足 |y(tj)-yj|≤C0N-2rα, j=0,1,2,…,n-1;n=1,2,…,N, 类似Case 1,可得|y(tn)-yn|≤C0N-2rα. Case3rα=1. 同理可得|y(tn)-yn|≤C0N-2lnN. 下面再考虑1<α<2的情形.假设存在常数C0>0满足 |y(tj)-yj|≤C0N-2, j=0,1,2,…,n-1;n=1,2,…,N, 同上可得 |y(tn)-yn|≤C0N-2. 综上,定理1得证. 考虑初值问题 (13) 其中,α∈(0,1)∪(1,2).该方程的精确解为y=tα. 对于不同的α∈(0,1)∪(1,2),选择r=1(等步长情形)和r=2(变步长情形)以及不同的N=16×2l,l=1,2,3,4,5.计算格式(7)的误差及收敛阶,结果见表1和表2. 表1 误差和收敛阶(q=0.4,α=0.6) 表2 误差和收敛阶(q=0.4,α=1.5)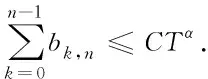

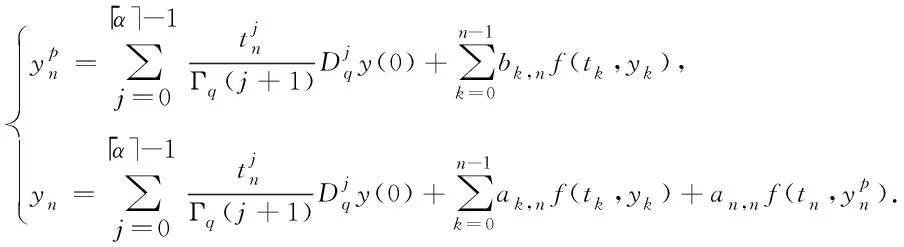
2.2 误差分析
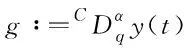
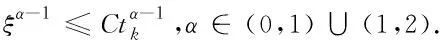
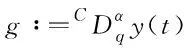
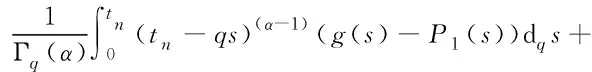
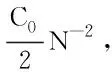
3 数值算例


