BOPPPS教学模式+对分课堂的大学数学课堂教学设计
2022-04-16单彩虹
陈 平 顾 娟 单彩虹
(陆军装甲兵学院 北京 100072)
0 引言
在坚持面向世界科技前沿、面向经济主战场、面向国家重大需求、面向人民生命健康,深入实施新时代人才强国战略下,高等教育院校承担着培育新型人才的重任。而作为高等教育之一的数学教育是培养学生的逻辑和抽象思维能力、几何直观能力、空间想象力以及对数学学科的自学能力和实际操作能力等,其教学原则是在教师主导的前提下,发挥学生的主体性原则[1]。作为大学数学基础课程的《线性代数》《高等数学》《概率论与数理统计》,所包含的教学内容在理工科专业起着重要作用。首先,随着大数据时代的到来和人工智能技术的发展,当代大部分新学科、新技术都兴起与数学和其他学科的交叉,数学思维和方法贯穿了一切科学领域。掌握一定的数学理论和模型,对学生的专业学习和未来发展有一定的影响;其次,大学数学教育旨在培养学生的科学精神、探索创新精神,同时注重将辩证统一的唯物主义精神、无私奉献的人文主义精神以及艰苦钻研的科研精神等潜移默化的渗透到课程教学中去。因此,大学数学课程是大学生学习生涯中至关重要的基础必修课程。
然而,大学数学课程相比初等数学课程课时较少,内容较多,使得以往的课堂教学以教师为主体,授课过程中多以传统教授为主,重知识讲解和逻辑推导,轻实际应用,使学生感到数学课程内容过于抽象,晦涩难懂,更谈不上提高学生的创新能力,所以必须转变教学思想和观念,以学生为主体,加强学生的数学应用能力,培养高素质有创新的新型人才。因此,将对分课堂和BOPPPS教学模式相结合,改革大学数学课堂教学设计内容,可以有效优化课堂教学效果,提高学生的自学能力,并树立其数学建模思想,增强学生的应用意识。
1 教学模式概述
BOPPPS教学模式是以建构主义和交际法为理论依据,以有效教学设计著称,它强调学生作为课堂的主要角色,应全方位参与式学习而不只是听讲;在课堂教学中,教师应及时获得学生的反馈信息,以调整后续教学活动以期顺利达到教学目标。在课堂教学过程中,教师可以借鉴这种模型,充分应用灵活多样、直观形象的教学手段,鼓励学生积极参与教学过程,使学生能深刻地领会和掌握所学知识。它将课堂教学过程分成了六个模块,分别是导言(Bridge-in)、学习目标(Objective/Outcome)、前测(Pre-assessment)、参与式学习(Participatory Learning)、后测(Post-assessment)和总结(Summary)[7]。
对分课堂[3]是一种新的课堂教学改革模式,它将课堂教学时间分成两部分。一部分时间以教师讲授基本知识、基本概念为主。教师在课堂中着重讲授课程重点、难点,但并不将课程内容和盘托出,给学生留白。学生利用另一部分时间进行学习讨论。学生通过教师提供的基本内容和课程重难点,根据自己的个人特点和具体情况自行完成内化吸收过程,针对个人情况对教材内容进行全面理解。内化吸收之后,学生回到课堂分组讨论自己学过的内容,然后与全班和教师进行深入的互动交流。同一内容,经过教师讲授、课后复习、分组讨论三个过程分阶段学习,理解程度逐步加深。对分课堂将教学过程分为讲授(Presenta-tion)、内化吸收(Assimilation)和讨论(Discussion)三个模块,也可简称为PAD课堂。
两种教学模式目的虽然都是促进学生积极参与课堂学习,但是对分课堂的教学模式侧重培养学生的学习能力,以及其交流、沟通、发表、见解等能力,而BOPPPS教学模式则重点描述了课堂教学各个环节的流程化体系,使得课堂教学的设计、开发和组织更加条理化、合理化和易操作化。因此将对分课堂和BOPPPS教学模式有效结合,可以有效激发学生主动学习能力以及团队合作精神,以及提高学生深度学习的水平。
2 基于两种模式下的“正态分布”课堂教学设计
以《概率论与数理统计》课程中的“正态分布”一节内容为例,将本节课进行对分课堂和BOPPPS教学模式的有效融合,结合幻灯片和计算机软件等信息资源进行教学设计。
2.1 导言──问题引入
在讲授理论知识前,为了吸引学生的注意力和提高学生的学习兴趣,首先介绍两个生动的实际案例,使学生认识到正态分布在实际生活中的普遍性。
引例1是2019-2020秋季学期大二某班学生的某次概率测试成绩,如图1直方图所示。引例2是对某大学男大学生的身高进行了实际调查,得到了如图2所示的关于这所大学男生身高的直方图。让学生了解到生活中的数据是可以用图形表示,并对正态随机变量的存在有感性认识。

图1:概率测试成绩

图2:男大学生身高
2.2 学习目标──对学生的要求
学习目标是让学生明确是为了让学生明确本堂课的学习任务,学习完本堂课后应该能做到什么。由于学习目标必须满足具体、可衡量、可达到以及和其他目标具有相关性等几个要求,因此,本节课的学习目标设计为以下几点:
(1)背诵正态分布(标准正态分布)的概率密度,并通过概率密度写出正态分布(标准正态分布)的分布函数;
(2)对照分布函数的性质,推测标准正态分布函数的性质;
(3)证明正态分布标准化定理;
(4)熟练运用正态分布的标准化定理进行计算。
2.3 前测──问答式
前测的目的是了解学生对本堂课程内容之前所学的相关基础知识的掌握情况。因此,采用了提问应答的方式给出了两个问题:分布函数的定义和性质是什么?引例1和引例2中的图形具有的共同特点是什么?
2.4 参与式学习──自学后进行小组讨论
参与式学习的目的在于让学生主动学习、深入思考、强化印象,要以学生为中心,因此这段时间教师不予讲解,提出几个思考题,先让学生自学。在自主学习结束后,带着问题和观点进行小组讨论。讨论结束后,将小组的观点整理成文字形式,选择一名学生向老师展示学习成果。如果在小组讨论过程中,问题得不到解答或者观点不统一的情况下,可留在答疑环节,由老师统一解答。在参与式学习中,学生可以参考教材、慕课等网课平台,或者通过互联网去搜索相关材料。
正态分布的思考题设置如下:
(1)正态分布中两个参数和的意义是什么?
(2)为什么要讨论标准正态分布?它的意义是什么?
(3)如何对正态分布进行计算?
(4)为什么正态分布具有三倍的标准差原则?三倍标准差原则在实际中有哪些应用?
(5)正态分布是由谁发现的?
(6)生活中还有哪些是正态分布?
学生通过小组间分享学习结果,进行归纳总结,对本节内容有了更深刻的理解体会。首先,通过分析图形进一步掌握以下知识:根据正态分布的概率密度曲线在x趋于无穷时会无限逼近于零,加深了对概率密度规范性这一知识的掌握;通过改变参数的大小,观察图形的变化,得出是位置参数,是尺度参数。当固定,改变的大小时,图形的形状不变,只是沿x着轴作平移变换;当固定,改变的大小时,图形的对称轴不变,而形状在改变。越小,图形越高越瘦,越大,图形越矮越胖。其次,正态分布在求分布函数时比较复杂,而标准正态分布分布函数可查表得到,因此将正态分布标准化后,可得到标准正态分布进行计算。第三,随机变量的取值几乎都落在这个范围内,这在统计学上称为三倍标准差原则。它的应用是六西格玛标准,其主要依据之一为正态分布。这个标准是20世纪80年代由摩托罗拉公司提出的概念和相应的管理体系,并全力应用到公司的各个方面,从开始实施的1986年到1999年,公司平均每年提高生产率12.3%,不良率只有以前的1/20,大大提高了企业业绩与竞争力。第四,法国数学家棣莫弗最早发现了正态分布的密度形式,由德国数学家高斯加以推广,正态分布的密度才以概率分布的身份引起人们的重视,因此正态分布也称为高斯分布。第五,正态分布是日常生活中最常见的也是最重要的一种分布。像学习成绩、测量误差、身高、体重、零件尺寸等都近似服从正态分布。
2.5 后测──课堂练习
后测是用来评估学生学习结果、检视学生是否完成学习目标。本节课主要采用了案例求解的形式进行测试学生学习成果。
案例1坦克驾驶室高度的设计。
问题提出:坦克是现代陆上作战的主要武器,有“陆战之王”之美称,它是一种具有强大的直射火力、高度越野机动性和很强的装甲防护力的履带式装甲战斗车辆。由于坦克内部配有武器系统、通信设备、三防装置等装置和设备,空间比较狭小,所以对于驾驶人员的身高也是有要求的,尽量不需要太高,也不能太矮,否则影响士兵对道路情况的判断。为此需要设计驾驶室的最低高度。人的身高服从,根据统计资料,对于中国人,=1.75,2=0.05。现要求舱内不能笔直坐姿的人不超过5%,问驾驶室至少需要多高?
在解答过程中,需要学生运用建模的思维方式解决此问题。需要考虑到在座位是固定的前提下,将问题转化为求士兵坐姿时从臀部到头顶的高度。可根据已知和黄金分割点求得从臀部到头顶满足要求的最小高度,加上座位的高度即为驾驶室的高度。本题的理论基础是正态分布的随机变量落入一区间概率的计算方法。先进行标准化,转化为标准正态分布后,通过查表即可获得相关概率。
模型建立:设驾驶室高度为h,士兵坐姿时从座位到头顶的高度为X,则X~N(1.75×0.382,0.052)=N(0.6685,0.052)(0.618位黄金分割点)。
根据题意


若座位高0.35cm,则驾驶室高度设计为1.1475米即可。
在此过程中可以要求学生运用计算机软件进行辅助计算。软件实现:可通过寻找标准正态分布的(下)0.995的分位点来实现,在Matlab软件中相关命令为norminv(p,mu,sigma)。第一个参数为正态分布的(下)p分位点的概率p,即P{Z 在Matlab命令窗口中编写命令: 案例2如何预测大学研究生考试中录取分数线及能否被录取。 问题提出:报考研究生考试,考生最关心的问题是:自己能否达到最低录取分数线?自己的考试名次如何?能否被录取?假设某大学2010年研究生招生准备录取160人,其中计划内110人,计划外50人,实际报考人数为630。考试满分500分,考后不久通过查分系统得到如下信息:考试平均成绩是230分,390分以上的考生有30名。某考生的成绩为301分,问他能否被录取?若被录取,能否是计划内学生? 问题分析:此问题即要求预测此次考试的最低录取分数线,以及这名考生的排名。一般的,成绩服从正态分布N(230,2),可以用样本均值230作为的估计,利用统计量和样本信息估计出,从而总体的分布确定后可讨论其他问题。 模型建立:先预测最低录取分数线.记最低录取分数为x0,设考生成绩为X,对一次成功的考试来说,X应服从正态分布,即X~N(230,2), 因为最低录取分数线x0的确定应使高于此线的考生的频率高于,即, 即最低录取分数线是294分。 下面预测考生A的名次,其考分x=301, 这表示成绩高于考生A的人数约占总人数的26%。即考生A大约排在130名,结论是考生A能被录取,但他排在110名之后,所以录取为计划内学生的可能性不大。 软件实现:此问题的关键是计算标准正态分布的分位点,可利用Matlab软件中norminv(p,mu,sigma)命令。第一个参数为正态分布的(下)p分位点的概率p,即P(Z 总结是引导学生对于本堂课程内容进行回顾和梳理,找出重点和难点内容加强理解、记忆的过程,因此教师先对本节课内容进行小结,然后提出问题,要求学生课下解决。设置问题为两个正态分布的随机变量还是正态分布吗?为什么?需要满足什么条件? 本次课堂教学设计以BOPPPS教学模式为主,将对分课堂融入参与式教学环节,两者有效结合。教师通过生活中的案例引起学生兴趣,给出明确的学习目标,让学生对本节内容有个初步了解。然后提出问题,加大学生的参与力度。通过查询资料和小组讨论进行自主学习,提高学生的中心地位,使学生在兴趣驱动下自觉积极的投入到课堂学习中,获得理想的学习效果。通过案例求解,建立数学模型,并运用计算机软件进行求解,锻炼了学生的动手操作能力,并通过课后思考题对学生知识进行拓展。在教学过程中,不应拘泥于某种特定的教学模式,将多种教学方法结合并灵活运用,为培养具有创新意识和创新能力的新型人才起到积极的推动作用。
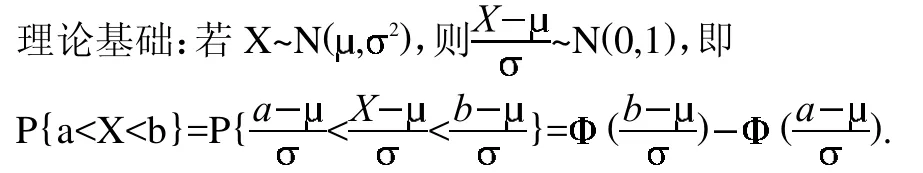




2.6 总结──小结加思考题
3 结论
