小学数学作业优化设计策略

高香琴

（福州市长乐区营前中心小学，福建 长乐 350200）

数学作业，既是夯实学科基础的重要手段，亦是培养学生理性思维、锻炼其解决问题能力的有效渠道。但是一直以来，由于受到“功利性教育理念”的影响，不少一线教师在布置作业时，常常以无差别化的“题海战术”为主，作业形式单一、内容乏善可陈、缺乏层次感和针对性。这类作业不仅无法满足各层次学生的需要，更加重了他们的学业负担，继而在过量、过难的作业中丧失学科热情和学习信心。正因如此，随着“双减”政策的不断推进，如何在小学教学中有效优化学科作业质量，做到“控量减负、提质增效”，帮助学生从机械化、无效化的重复性作业中摆脱出来，［1］已经成为教育领域的研究热点。为了落实这一目标，本文围绕如何在“双减”背景下优化小学数学作业设计展开探讨。

一、知识迁移，凸显作业的前导性

前导性作业是教师在授课前，鼓励学生在预习新课的同时，尝试运用已学知识推导新知、理解数理知识，以达到高效地吸收新课的目的。在以“生本”理念为核心的“双减”背景下，教师可以根据学生的最近发展区，适当设计一些前导性作业，引导他们利用知识迁移，对新课内容进行自主探究，继而在适当的“挑战”中，获得能力提升。值得注意的是，为避免给学生加重负担，在设计该类作业时，教师应当遵循“量少而精”的原则，确保作业的针对性。

例如，在学习《除数是两位数的除法》时，结合教材例题及儿童感兴趣的话题，设置了以下作业：

题1 是针对除数是一位数的除法的算法与算理进行复习、强化，有助于学生新旧知识的衔接，以实现方法与技能的迁移。题2 是让学生在掌握除数是一位数的除法的计算方法后，自主探究，尝试计算除数是两位数的除法，以此提升学生的推演能力。

在教学中，适当引入前导性作业，不仅能够巩固旧知识，还能够引导学生在“熟悉与陌生”的中界线上，运用合情推理法，对新知展开探究，促使他们在知识迁移的过程中，真正吃透除法的算理，突破教学难点，完善学科知识结构。

二、聚焦生活，增强作业的趣味性

“数学源于生活，又应用于生活”。在小学阶段的数学教学中，教师将学科作业与生活相联系、相渗透，不仅能够让抽象的数学知识变得具体可感，增强学科作业的趣味性，减轻学习数学的枯燥感与畏难情绪，拉近学生与数学作业之间的心理距离；还有益于转化学生的视角，引导他们用数学的眼光看待生活，用数学的思维解决生活问题。应用性强、趣味性高的学科作业有助于逐渐激发学生主动学习的内在驱动力。

例如，在人教版六年级“圆的面积”一课中，为切实提升作业的趣味性，深化学生对知识的理解与应用，笔者将数学知识与生活问题合理融合，以“餐桌上的数学问题”为主题，设计了以下趣味性作业：

李阿姨想给家中圆形餐桌铺上一张桌布（桌布大小与餐桌面积一样），她测量了三组数据：

A：桌子边缘周长是3.768 米；

B：桌布对折一次后折痕长1.2 米；

C：桌布对折两次后折痕长0.6 米。

1.如果你是李阿姨，你会选择哪个数据，购买合适的桌布？说说你的理由。

2.圆形桌布是从一块正方形的布料上剪下来的，你觉得正方形的边长至少要多少米？剪下圆形桌布后剩下的布料是多少平方米？（请先画出示意图，再列式计算）

3.（1）如果在餐桌中间摆一个圆形转盘（见图1），转盘的半径尺寸有：①6.5 分米②5 分米③2 分米。你觉得选哪一种比较合适？请说明理由。

（2）李阿姨家的圆形菜盘子直径是20 厘米，这张转盘最多能摆下25 个盘子吗？说说你的想法。（请动手画一画、摆一摆）

第1、2 小题，主要考查学生对基础知识的掌握情况。第3 小题的第（1）问，学生根据题目提供的数据，要结合生活实际才能做出正确的选择。第（2）问，虽然学生都能通过计算求出转盘的面积和25 个圆盘的面积总和，但是由于部分学生缺乏一定的生活经验，忽略了圆形之间的摆放要有空隙，即圆不能密铺的特性，容易做出错误判断。本题通过创设贴近生活、生动有趣的问题情境，充分调动学生的探究兴趣，使学生感受到生活中处处有数学，培养学生乐学数学、善学数学。

三、关注差异，体现作业的层次性

遵循教育规律，以“学生为本”，是贯彻“双减”政策的基本原则。由于个体间的思维方式、知识基础及认知能力存在较大差异，学生的数学学科素养也有较大差距。在日常教学中，教师必须正视并尊重这种差异性，以“学习能力”为切入点，通过合理设计适量的、具有不同梯度和难度的作业，满足各层次学生的学习需要。［2］不仅帮助学生摆脱无效的、不符合其学情的作业，还促使他们在个性化的数学作业中，逐渐强化自身的学科素养，进而落实“让各层次个体均有所益”的施教理念。

例如，在教学《圆锥》时，为了使每个学生都能学有所得，笔者根据不同层次学生对知识的掌握情况及自身的思维水平，设计了以下一组难易有别的梯度性作业：

请根据图2 的直角三角形，完成《圆锥》学习作业单（见表1）。

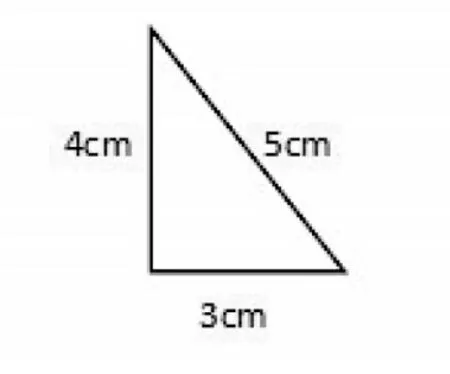
图2

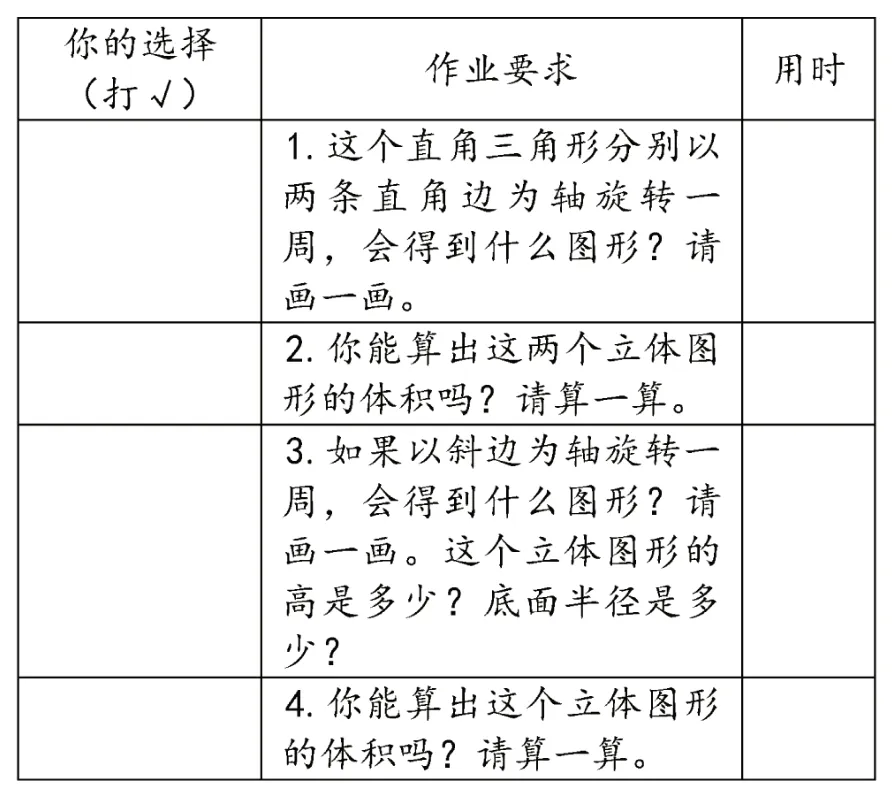
表1 《圆锥》作业单

本道题组中，因为之前在认识圆锥时，通过多媒体动态演示，学生已直观地看到直角三角形快速旋转形成圆锥的过程，所以大部分学生都能比较轻松地完成第1、2 两道基础题，既巩固所学知识，又增强他们学习数学的自信心。题3、题4 有一定的难度，富有挑战性，能充分激发学生的探索欲望。一些优秀的学生具有丰富的空间想象力，能想象出以斜边为轴旋转时形成的图形形态——两个有公共底的圆锥，它们以斜边的高为底面半径，高的和为斜边的长。这样有层次性的作业设计，有助于深化学生灵活运用学科知识的素养，提升他们的空间想象能力和探究精神。

教学实际中，教师秉持因材施教的理念，通过适量、适度、有弹性的分层作业，对不同层次的学生进行梯度训练，减轻学生的作业负担，精准提升其数学素养，进而实现优化提质、分层增效的作业设计目标。

四、发散思维，强调作业的开放性

从以往的教学经验来看，很多教师倾向于布置一些形式单调、解法单一的单向式作业。这不仅容易让学生陷入思维定势与学科知识应用能力不足的困境，还有碍于其发散思维与多向思考能力的发展。在小学阶段的数学教学中，为有效转变这一现状，教师可以适当设计一些多向发散型的开放题，引导学生在一题多解、一题多变和一题多思中，学会抓住数学本质，懂得灵活变通，突破思维惯性，进而形成多维度思考的横纵联想能力，以达到强化发散思维、拓宽思考广度、提升解题能力的目的。

例如，教学《轴对称图形》后，为锻炼学生的发散思维，教师设计了以下开放性作业（见图3）：

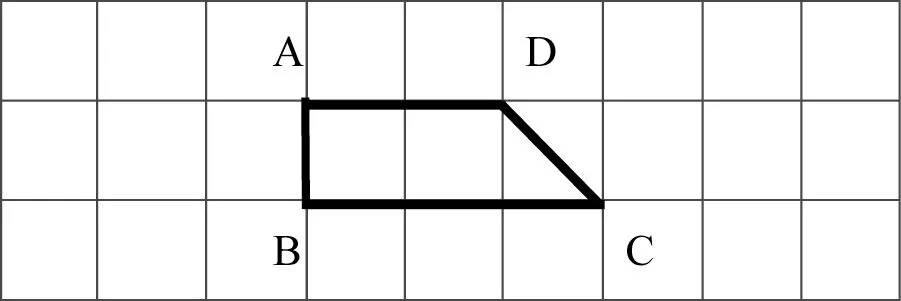
图3

下图是轴对称图形的一半，你能用哪几种方式补全这个轴对称图形，并画出它的对称轴？

本题的解法与思考方向具有多元化的特征，开放性较强。在具体解题过程中，学生的解法如下：

（1）根据“横纵方向的直线为对称轴”的常规思路，多数学生都能以线段“AD”“AB”和“BC”所在的直线为对称轴，画出轴对称图形；

（2）部分学生对上述方法进行发散拓展，补充了以斜边“DC”为对称轴的轴对称图形；

（3）个别学生突破“以现有直线作为对称轴”的思维模式，对已有解法进行深度发散延伸。即先根据解法（1）（2）得到对称图，再以某一公共顶点为中心，将梯形ABCD 旋转90°，便得到以其旋转角的角平分线为对称轴的轴对称图形。

通过开放性作业的设计，引导学生从多维度分析数学问题，从多层面探究数量关系，拓宽学生的思维广度，强化其发散性思维与逻辑推理能力。

五、深化素养，提高作业的探究性

探究性作业是指学生在具有一定探究性的数学问题的引导下，根据自身已有的知识储备及思考模式对知识展开探索，从而深化数学素养的一类作业。在以“学生为本位”的“双减”背景下，为提升学生的学科素养，培养实证精神与理性思维，在日常的作业设计过程中，教师可以适当设计一些具有“探究性”的作业，引导小学生充分调动自身已有的知识经验及思考能力，探究、发现规律，解决数学问题，培养探究素养与实践能力。［3］

例如，在教学“长方形的周长”一课后，为培养学生的逻辑推理、数学表达、创新思考等综合应用能力，笔者设计了以下作业：

刘大爷想用16 米长的篱笆靠墙围成一个长方形的鸡舍（如图4），可以有几种不同的围法？哪种围法的面积最大？是多少平方米？请说明理由。（鸡舍的长、宽取整厘米数）

学生小组合作，采用列表法和枚举法，把不同的围法一一呈现（见表2）。通过对数据的观察、分析、思考、合作交流，在教师的引导下，得出结论：（长+宽）的和一定时，长与宽的差越小，长与宽的乘积即长方形的面积就越大。

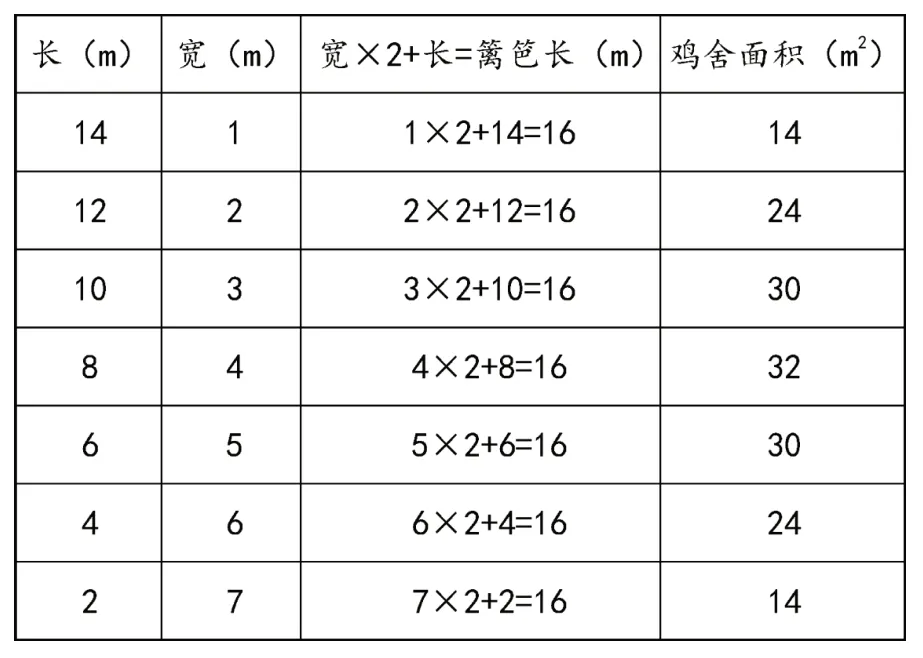
表2 不同的围篱笆方法的数据

教学中，学生通过合作交流，共同完成实验探究性作业，不仅有益于培养合作意识、勇于探索的实证精神，而且在切实拓展思维能力、培养思维素养方面亦有显著成效。

在“双减”背景下，为了提升数学课业的质量、减轻学生负担、增强教育的实效性，教师在设计作业时，应当注重因人而异，为不同层次的学生布置适量的、符合其学情的梯度性作业。通过创新作业形式，引入前导性作业、将作业生活化以及设计具有探究意义的实践作业等策略，以优化学科作业，贯彻“双减”政策。