基于动态稀疏注意力的地铁客流预测模型*

马 茜 梁 奕 段 毅 曾尚琦

(1.西咸新区轨道交通发展有限公司，710086，西安；2.南瑞集团(国网电力科学研究院)有限公司，210003，南京；3.国电南瑞科技股份有限公司，211106，南京∥第一作者，高级工程师)

地铁客流的精准预测可帮助优化行车间隔和制定合理的运行方案。然而，影响客流的变量在时间和空间上存在不均衡性，表现为：时间序列的高峰平峰，日、周、月客流以及空间存在位置性和方向性，包括车站、线路、线网瞬时和历史数据(部分受气候条件的影响)。其动态复杂度显著提升。

目前针对客流的时间序列预测，主要基于历史客流进行预测建模。随着深度学习表征能力的增强，深度学习技术在时空数据预测领域得到广泛应用。RNN(递归神经网络)可捕获客流的时序依赖关系[1]。CNN(卷积神经网络)结构侧重于空间特征，却丢失了时间维度信息[2]。ConvLSTM(卷积长短记忆网络)将RNN和CNN的架构结合起来，将全连接层替换为卷积层[3]来捕获时空相关性；然而，ConvLSTM在状态转换中使用卷积，相当于把循环连接结构模型变为时空恒定结构模型。总之，客流预测仍存在复杂非线性建模、动态关联及计算复杂度等亟待解决的问题。

在周一早高峰时段，进站客流特征大致相同，体现了短期模式和局部数据紧密相关性；在其余工作日的早高峰及晚高峰时段，进站客流特征大致相同，体现了长期模式和全局数据稀疏相关性。对此本文提出DSANNs(动态稀疏注意力)模型，利用全局变量注意力自动选择相关驱动序列，增强模型预测的判别性；根据局部数据紧密相关性和全局数据稀疏相关性的先验知识，对历史时间步和相关变量分别卷积和稀疏卷积，提取局部时间和变量特征，并设计稀疏注意力对相关时间步加权和变量加权，进而提高客流预测的准确性。

1 客流预测的影响因素

现有的地铁客流预测研究通常基于历史数据进行，其预测结果完全依赖于历史数据的准确性，并未挖掘多种监测指标之间存在的内在复杂关系。客流预测主要受以下因素影响：

1)长短周期时间依赖的关联。进出站客流的多维时间序列蕴含一种局部紧密和全局稀疏相关的内在关联，混合着长短周期时间依赖关系。变量的变动可分为趋势性、周期性、随机性及循环性变动。客流预测需过滤随机性变动，仅反映时间序列中的趋势性变动和周期性变动，综合捕获时间序列数据中长短周期时间依赖关联。

2)变量的动态相关性。各维度变量之间的相关性是动态的，即动态相关性。车站的进出站客流、线网拓扑、天气状况和空气质量等变量间均存在动态相关性，而且进、出站客流间的相关性强，客流与温度的相关性弱。可见，测点各维度变量的时间序列数据对于客流预测的影响并不一致。测点监测每项指标的时间相关性也是动态的：非高峰时段的客流数据差异不大，相关性较强；在高峰时段，测点的监测数据可能存在较大差异，相关性较弱。此外，测点监测数据也可能存在周期性变化规律，因此需要选取合适的数据统计时间间隔。

3)数据受到外部因素的影响。各变量的时间序列数据对目标预测序列数据的驱动作用不仅随时间的变化而变化，还会受外部因素的影响。恶劣环境因素及特殊活动等事件因素，都会导致时间序列数据出现突变、陡降甚至是拐点。

2 DSANNs模型

为了捕获变量多维时间序列中长短周期时间依赖关系和动态性，针对客流预测的影响因素，本文提出DSANNs模型。如图1所示，DSANNs模型包括全局变量注意力机制的编码器、局部变量稀疏卷积注意力机制和全局时间卷积稀疏注意力的解码器。

注：LSTM为长短时记忆网络；Attn输入指注意力机制输入。

1)全局变量注意力机制自适应地选择相关驱动序列，增强预测的判别性，捕获动态全局变量相关性。

2)局部紧密、全局稀疏的全局时间卷积稀疏注意力机制对变量多维时间序列中相关时间步蕴含的信息加权，提取各时间步下的内在局部特征。稀疏注意力可减少关联，降低模型复杂度，防止过拟合。

3)局部变量稀疏卷积注意力会自动选择相关变量进行加权。经过稀疏卷积核提取的局部特征可以理解为每个变量在固定的时间窗口形成的局部内在关系。通过局部变量注意力，将所有横跨固定窗口的时间序列数据信息整合。

4)将相关的外部时间特征、气象特征、目标测点的相关属性等特征因素合并为1个低维向量嵌入到模型中。

2.1 全局变量注意力

在预测过程中，时间序列同输入序列数据和目标序列数据的相关程度并非一致。基于每个测点输入序列数据得到的对一时刻预测数据是随时间动态变化的。全局变量注意力机制设计如图2所示。

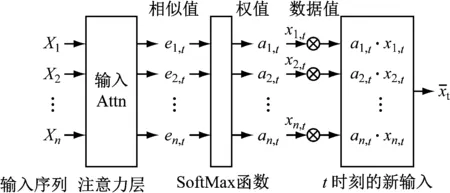
图2 全局变量注意力机制

全局变量注意力机制能自动判定输入序列每个时间步下各序列对目标序列预测的重要程度，突出与当前预测任务最相关的输入变量，弱化与任务预测无关的输入变量。

编码器将输入序列编码成机器翻译中的特征表示[4]。第k输入序列Xk=(xk,1,xk,2,…,xk,T)∈T，xk,t∈n×T表示在驱动序列k时间戳t下的数据值，n为驱动预测序列的数量，T为历史时间序列的长度。该编码器用来学习从xt(xt∈T)到ht的1个映射函数，可表示为

ht=f1(ht-1,xt)，ht∈m

(1)

式中：

ht——编码器在时间步为t的隐藏向量，蕴含t时刻前的历史信息，m为该隐藏向量大小;

f1——非线性激活函数。

DSANNs使用LSTM单元作为非线性激活函数f1去捕获原始时间序列中的长期依赖关系。将其与历史时间步隐藏层状态ht-1和LSTM中的细胞状态St-1进行匹配，得到该时间步下驱动预测时间序列的各变量重要性，故有：

ek,t=vetanh(We[ht-1,St-1]+Uexk)

(2)

式中：

ve,We,Ue————均为调优的超参数，且ve∈、We∈T×2m、Ue∈T×T；

ek,t——在时间步t下衡量第k输入序列的相似性值；

ak,t——通过SoftMax函数得到的注意力权值，且所有ak,t归一化和为1。

输入注意力机制通过前馈神经网络和递归循环神经网络部分一同训练，得到驱动预测序列随着时间演变的权重，并在每一个时间步自动选取最重要的特征进行预测，同时调整时间步t下隐藏层状态向量。具体为：

(3)

2.2 动态稀疏注意力

每个时间序列在固定窗口大小为ω的数据对目标预测序列预测的重要性不同，往往蕴含着一种局部紧密相关和全局稀疏相关的内在关系，而密集全局关联任务是很少的。因此，基于局部紧密相关和全局稀疏相关的内在关系，DSANNs中设计了2种注意力机制(如图3所示)，分别对变量和时间进行卷积操作和注意力权值分配。

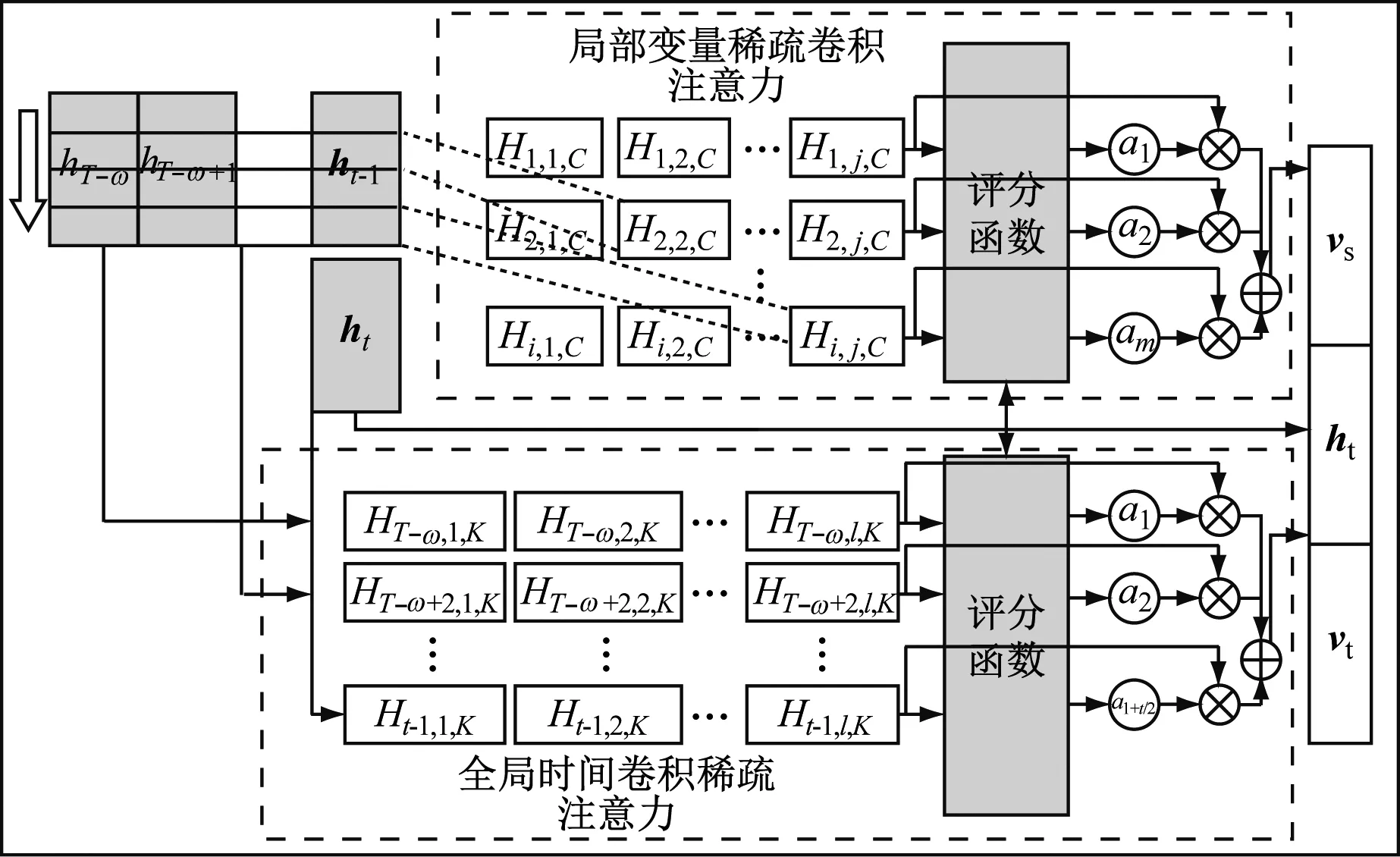
图3 DSANNs模型的注意力机制

2.2.1 局部变量稀疏卷积注意力

DSANNs模型利用卷积核卷积编码后的时间序列，增强学习到时间序列的局部变量内在关系。设计卷积核Cj∈T。(Cj,T-ns,…,Cj,T-2s,Cj,T-s,…,Cj,T-1,Cj,T)≠0,T-ns≥1，s为局部紧密全局稀疏程度。

卷积核卷积每个变量，捕获其局部紧密相关和全局稀疏相关的内在特征。全局变量注意力机制的隐藏层向量表示H∈m×T经过卷积操作，最终的变量维度为HC∈m×k。其中,k代表k个具有不同内在关联关系的类似卷积核,m代表每个时间步编码后变量的维度。RELU是激活函数RELU(x)=max(0,x)，故有：

(4)

式中：

Hi,j,C——卷积核对隐藏层向量提取结果；

Cj,T-ω+p——第j卷积核；

Hi,(T-ω+p)——隐藏层第i行向量；

bjC——偏差的参数。

局部变量稀疏卷积注意力选择相关变量进行加权，将时间序列数据整合成1个固定尺度的向量vs：

ai=sigmoid(Hi,Cht)

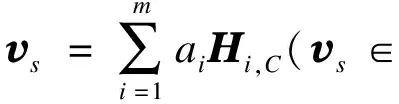
(5)

式中：

Hi,C——卷积后第i行隐藏层行向量表示；

ai——sigmoid函数计算注意力权值。

由式(5)，通过权重对HC重新分配得到隐藏层向量vs。

2.2.2 全局时间卷积稀疏注意力

时间序列数据通常混合长期和短期模式，并且时间序列中历史时间步蕴含的信息对目标预测的重要性不同，往往蕴含着一种局部紧密相关和全局稀疏相关的内在关系。DSANNs根据此先验知识，利用卷积神经网络提取各变量序列中的短期局部变量，构建稀疏注意力捕获时间序列中的局部紧密相关和全局稀疏相关的内在关系。

全局时间卷积稀疏注意力自动选择相关时间步加权。卷积核提取所有变量在每一个时间步的内在局部特征，通过全局时间稀疏注意力，将所有横跨固定窗口的时间序列数据整合成一个固定尺度的低纬度向量vt。vt为固定尺度的上下文向量，具备时空特征。则有：

(i=1,3,…,t-5,vt∈l)

(6)

式中：

Hj，K——卷积后形成的第j时间步隐藏层列向量表示；

aj——自动选取时间步计算注意力权值。

提取各时间步下的内在局部变量特征后，通过局部紧密相关和全局稀疏相关的注意力机制，对单测点多维时间序列中相关时间步蕴含的信息加权，捕获时间序列短期和长期依赖关系。

2.3 模型预测

DSANNs模型包括：局部变量稀疏卷积注意力提取的、相关变量加权的、隐藏层向量表示vs，全局时间卷积稀疏注意力提取的、相关时间步加权的、隐藏层向量表示vt，全局变量注意机制的隐藏层向量ht。通过多层感知机，得到最终预测结果：

γt=Whht+Wsvs+Wtvt

(7)

式中：

Wh，Ws，Wt，Wγ——分别为各隐藏层的权重参数，Wh∈m×m，Ws∈m×k，Wt∈m×l，Wγ∈(n×Δ)×m

3 试验与分析

为了测试不同变量多维时间序列预测方法的性能，采用基于Python语言和Keras深度学习框架开发的DSANNs，以某城地铁站点的月度客流量为例，进行试验。按照10 min聚合1次，则聚合数据总计4 464条。

3.1 试验配置

1)参数设置。通过窗口大小进行网格搜索“ω={3,5,10,15,25,50,72,100}”，确定时间窗口ω；对隐藏层进行网格搜索“m={16,32,64,128,256}”，确定隐藏层m；为了确定不同注意力卷积核个数带来预测表现的变化，设置k=l，对卷积核个数进行网格搜索“k=l={16,32,64,128}”，最终参数选择验证集的最佳性能参数。

2)评价指标。为了衡量各种时间序列预测方法的有效性，考虑了均方误差EMS、平均绝对误差EMA及平均绝对百分误差EMAP等3种不同的评价指标。

(8)

3.2 结果分析

在客流多维时间序列数据集上将DSANNs模型同ARIMA(差分整合移动平均自回归)模型[6]、LSTM模型[7]、ConvLSTM模型[3]、TCN(时间卷积网络)模型[8]、DA-RNN(注意力机制-递归神经网络)模型[9]进行比较。各模型的时间序列预测效果如表1所示。

表1 各模型对单测点多维时间序列的预测结果评价指标

从表1可以看出：基于实测数据，采用DSANNs模型得到的EMA、EMAP和EMS最佳，与采用DA-RNN模型的结果相比分别降低了21.07%、18.47%、29%；与LSTM模型相比，ARIMA模型的预测精度较差，这是因为ARIMA模型只考虑目标序列，忽略了其他相关维度的驱动序列；ConvLSTM模型、TCN模型结合了时间和变量的相关模型，预测表现要优于单纯捕获时间依赖的LSTM模型；DA-RNN比采用卷积和长短记忆网络的ConvLSTM模型、TCN模型的性能更好，因为它关注了时间和变量的动态性。综合来看，DSANNs模型表现最优。这主要因为DSANNs模型通过局部紧密全局稀疏的时间注意机制以及相关变量的注意力机制，捕获了时间动态性和变量的动态内在关系，提高了预测准确性。图4展示了对比基线最佳的DA-RNN模型和DSANNs模型在地铁客流流量数据集的预测结果。

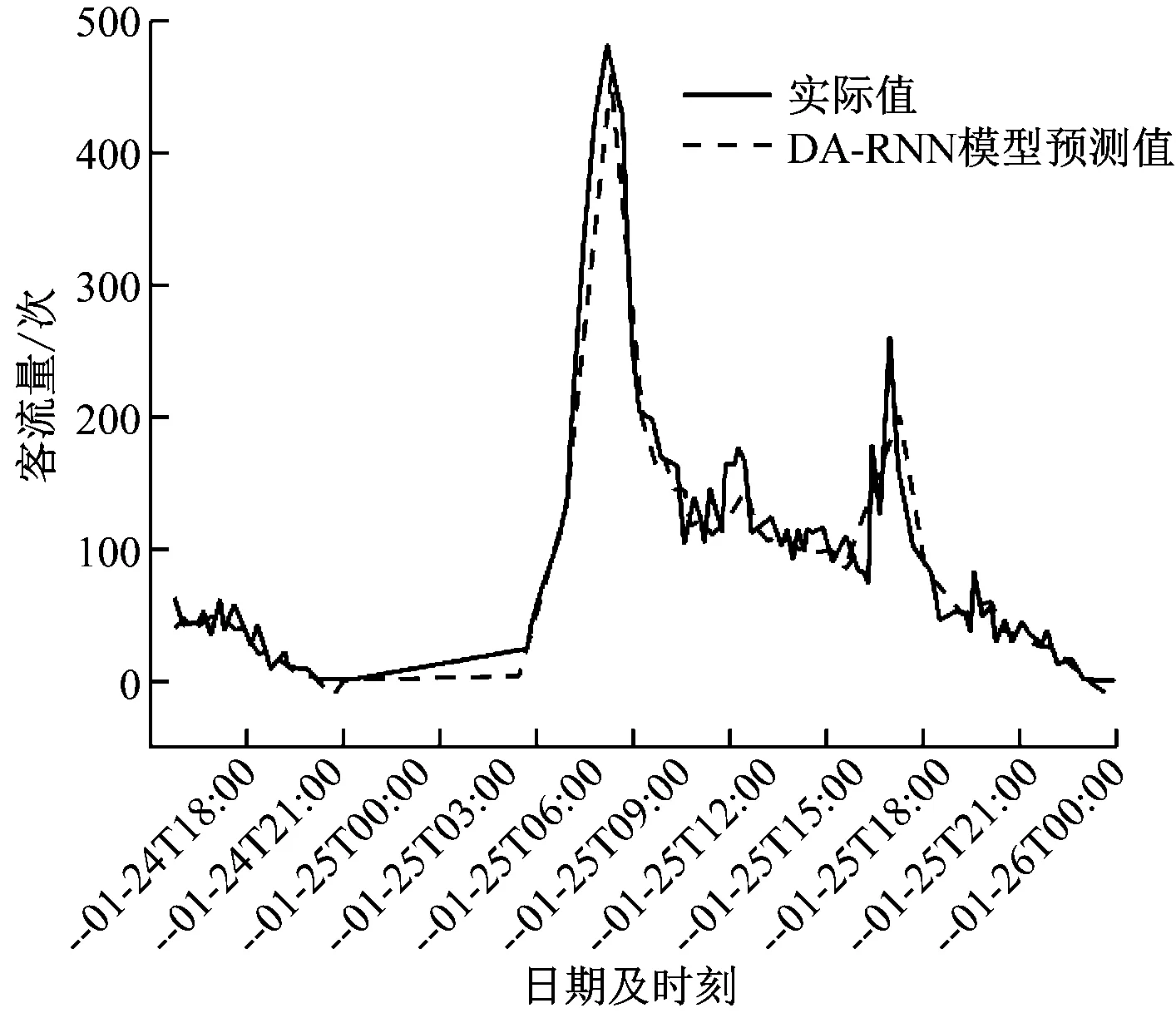
a)DA-RNN的地铁客流预测及对比

与DA-RNN模型相比，DSANNs模型在捕获时间动态性和变量内在关系方面表现更好，预测性能也更佳。经分析，DSANNs模型通过全局稀疏局部紧密的时间注意力机制的权重分配，减少关联性后，加大了全局稀疏的权重分配，使得模型整体的预测效果良好。

4 结语

客流预测需要预测地铁车站的潜在流量，表现为随时间演变的多维时间序列数据，受到外界复杂因素的影响而发生动态变化。通过分析客流的时空特征，提出DSANNs模型。DSANNs模型自动提取动态时间和变量维度的内在关系。其中，全局变量注意力机制自适应地选择相关驱动序列，增强了模型预测的判别性；稀疏注意力对相关时间步加权，注意力机制对相关变量进行加权，不仅能够从全局和局部捕获动态内在时间和变量关联，提高模型预测准确性，也能减少计算的复杂性。相比于ConvLSTM模型、TCN模型、DA-RNN模型等，DSANNs模型具有明显优势。未来可将时空数据预测模型和时序图进一步结合，提高图神经网络的预测准确性。