基于HHT 的高陡边坡爆破振动规律研究

王 旭

（中铁十九局集团矿业投资有限公司，北京 100176）

随着露天开采深度的增加，确保高陡岩质边坡稳定安全便成为露天开采生产过程中尤为重要的任务之一[1-2]，而且露天矿山边坡在开挖生产过程中不断受到爆破动载荷的侵扰，爆破动载荷对矿山边坡稳定性造成了一定的影响[3-4]。因此，研究高陡边坡爆破振动规律对于保证矿山安全生产以及边坡稳定具有重大意义。迄今为止，我国国内学者对爆破动载荷作用下的边坡稳定性以及爆破振动信号做了大量的研究。周子涵等[5]通过建立爆破动荷载作用下的露天边坡失稳尖点突变模型，开展了爆破振动振幅与频率对露天边坡稳定性影响研究，确定了边坡失稳判据与自稳高度，对保证降低爆破开挖对边坡岩体的破坏影响起到了指导作用；王文才等[6]针对高村露天铁矿开挖生产过程中存在的边坡失稳等问题，进行了爆破振动信号监测与处理，针对性地提出了高村露天矿有失稳倾向的边坡爆破振动波传播公式；尹久清[7]以云南小龙潭布沼坝露天矿为背景，对爆破振动信号进行监测与分析处理，提出了爆破振动速度预测计算公式，明确了边坡安全允许振速；张耿城等[8]通过现场监测与数值试验，分析了爆破振动规律与边坡受爆破振动作用下的动态响应特征，测点的垂向速度远高于水平方向，研究得出爆破振动强度与正高程成正相关；李祥龙等[9]以金沙矿业官房矿区402 矿段为背景，通过采用EMD－HHT 和小波理论研究了地下浅孔爆破振动规律，爆破振动信号能量分布呈正态分布，且最大瞬时能量与最大单响药量呈正比关系；张其虎等[10]为解决金沙矿业官房矿部分区段在进行爆破过程中振动强度过大的问题，采用EMD－HHT 研究了振动信号频率、振幅以及能量分布等爆破振动特征与规律。基于此，以某露天矿高陡岩质边坡实测的爆破振动信号为工程背景，基于HHT 方法对爆破振动信号的能量分布以及传播规律进行了研究。

1 工程概况

研究区露天矿高陡岩质边坡工程地质条件十分复杂，形成了各种缺陷，边坡内部节理发育。边坡岩体主要由泥质白云岩、泥质灰岩、凝灰岩等组成，边坡较稳定，属于Ⅱ类岩体边坡。边坡由5 级台阶组成，总体高度为42 m，坡度大于60°，台阶自上往下高度依次为5、7、9、10、11 m。现场爆破主要采用乳化炸药，起爆方式为电雷管延时逐孔起爆。边坡现场如图1。

图1 边坡现场

2 爆破振动信号监测

监测采用TC－4850 爆破测振仪为爆破监测设备，TC－4850 爆破测振仪是由成都中科测控有限公司生产，具有体积小、质量轻、耐压抗击等优点。爆破测振仪在爆破进行测点布置时遵循以下基本原则：①选取测点位置具有良好的边坡代表性；②测振仪确保安装在加速度计钻孔口的基岩上；③提前处理测点（通过石膏对钻孔进行凝固处理）；④各个爆破测振仪测点的岩体物理力学性质要大致统一；⑤测振仪要杜绝安装在褶皱及断裂带处；⑥各个测振仪都应布置在地质构造特征相似的区域内。根据现场测试条件，本次监测运用了6 台TC－4850 测振仪对该矿多次爆破进行爆破监测，监测点分别布置在临近爆区的基岩上。

为更好的分析爆破振动规律，每个测点位置都安装3 个方向（垂向、径向和切向）的振动速度传感器来监测爆破振动的三向振动值。采用此方案连续测试4 d，且每天都根据同一测点不同传感器型号进行数据采集并记录。三向爆破振动波形监测结果如图2。

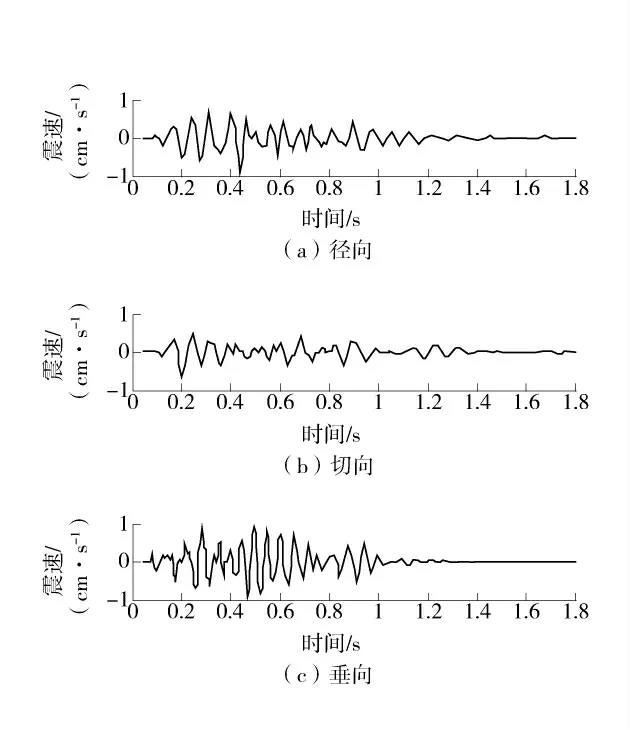
图2 三向爆破振动波形监测结果

3 基于HHT 的爆破振动信号分析

希尔伯特－黄变换（HHT 法）是一种被认为是处理非线性、非平稳信号的数据分析方法。HHT 的理论基础源于Hilbert 变换，它由经验模态分解方法（EMD）和希尔伯特（Hilbert）变换2 部分组成：首先根据EMD 得到有限数目的固有模态函数（IMF），然后应用Hilbert 变换和瞬时频率方法获得信号的Hilbert 谱，进而获得反映信号特性的边际谱和瞬时频率，即信号能量在空间（或时间）不同尺度上的分布变化规律。

3.1 爆破振动信号的EMD 分解

首先对已经收集好的原始信号进行处理，得到原始信号的各个极值点。接着通过运用3 次样条函数统一对每个极大值点和极小值点进行插值拟合，从而得到原始信号的上包络线和下包络线，其中上、下2 条包络线可包含全部信号数据。然后依次将上、下包络线的平均值连接便可得到均值曲线。最后再用原始信号曲线减掉均值曲线得到1 个新的信号曲线。对于不一样的信号，该信号可能是1 个IMF 信号分量，也可能不是；如果这个信号未能达到IMF所必备的要求，便可将这个信号当作原始信号，重新进行以上操作，直到找到IMF 信号分量。

基于EMD 原理和Matlab2009b 语言平台，运用EMD 程序对TC－4850 监测到的原始信号进行处理，从3 个不同方向（径向、切向、垂向）对原始信号进行EMD 分解，三向振动信号EMD 分解图略，从图中可以明显看出EMD 分解出的IMF 信号分量都有清晰的物理意义。

由EMD 分解图可知，三向振动信号进行EMD分解处理后，共计得到10 个IMF 分量信号。通过对各方向分量信号做频谱研究，能够得到IMF 分量信号的频率信息。IMF1 分量频率最高，所占能量非常小，表明它是在监测中引入的高频噪声，需在分析中去噪。IMF2 分量频率较高，IMF3 分量～IMF9 分量频率慢慢减小，说明地震波在快速传播的过程中高频显著降低。分量IMF2 分量～IMF5 分量振幅逐步增加，且包含了信号的大部分能量，说明建（构）筑物受到震动的影响逐渐加大，IMF5 分量～IMF9 分量震幅逐渐减小，说明建（构）筑物受到爆破震动最大能量后影响逐渐减小。最后的余量IMF10 表明监测仪器的漂零或信号微弱的变化趋势。振动信号在径向、切向、垂向方面经EMD 分解后得到的IMF 分量有着一致性。

3.2 Hilbert 谱分析

通过将EMD 方法分解后得到多个IMF 的信号组合进行Hilbert 变换，可得到每个IMF 分量的瞬时频谱，由它变换得到的瞬时频率频谱具有明显的物理意义。

在实际爆破振动监测中，监测仪器记录的振动数据不是单一的爆破信号，信号中掺杂了检测点周围环境影响信号。单一的爆破振动信号的频率为0～150 Hz，而建筑的固有频率在0～20Hz。从图3 可以看出，IMF1 分量为明显的干扰频率或噪声，在对信号进行Hilbert 谱分析时要先对信号进行滤波、消噪等处理，更好的反映爆破振动信号的真实内容。所谓的消噪处理是指通过分离噪声和信号的时频谱区域，采用适当的滤波方法将噪声从信号中清除或减弱，从而得到较高的信噪比和获取更有用的信息，进而使各IMF 分量经Hilbert 变换后的频谱图更好地反映爆破震动的情况，使Hilbert 谱也有更有意义。

1）瞬时能量谱。瞬时能量谱是由EMD 分解处理后求得的IMF 各分量经Hilbert 变换后求得。瞬时能量谱清晰地显示了振动信号的能量与时间的关系。Hilbert 瞬时能量谱如图3。从图3 中可以看出波形的最高值表示为瞬时能量的极值，其波形范围集中在0.2～1.0 s 区域内。瞬时能量的物理意义为爆破的最大荷载值，瞬时能量的大小与爆破荷载的大小呈正相关。

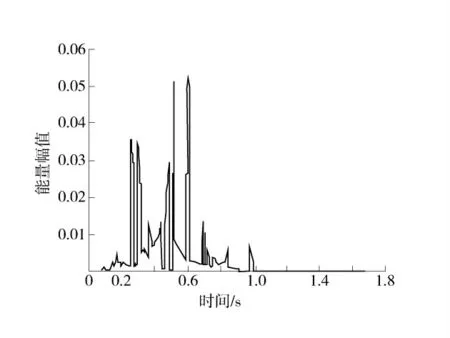
图3 Hilbert 瞬时能量谱

2）Hilbert 能量谱。Hilbert 能量谱是由瞬时能量谱经过分析处理后得到，即对振动信号振幅先平方后再进行时间积分。Hilbert 能量谱可以准确计算各个频率所对应的能量，它所涵盖的物理意义是在全部时间段内各个频率积累的所有能量。Hilbert 能量谱如图4。由图4 可知，爆破振动能量分布范围为0～100 Hz，且大部分能量集中于50 Hz 以下的低频段区；而强度高于50 Hz 以上的频段，其爆破振动能量分量很少。

图4 Hilbert 能量谱

3）Hilbert 边际谱。能量边际谱通过将能量谱在时间域内积分便可求得。能量边际谱表示的是振动信号的能量随频率增加的变化情况。求得的Hilbert边际谱如图5。由图5 可知，Hilbert 边际谱清楚地表明了爆破震动以低频为主，其主震频带在0～15 Hz范围内。

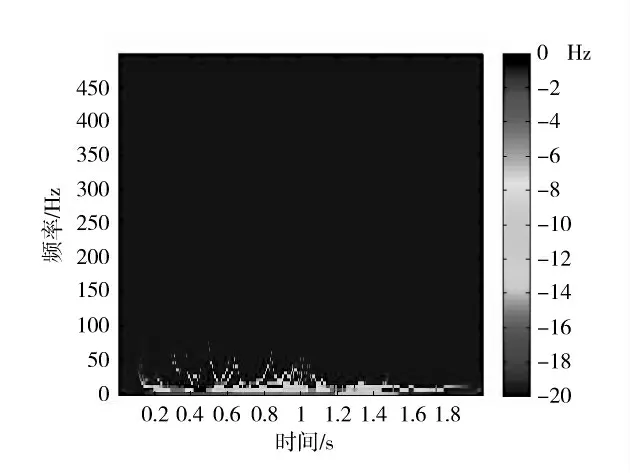
图5 Hilbert 边际谱

4 结语

对某露天矿高陡边坡开挖过程中所产生的爆破振动信号进行了监测，采用HHT 方法对高陡边坡振动监测信号进行处理，研究了IMF 分量、Hilbert 瞬时能量谱、能量谱、边际谱，得出边坡爆破振动以低频为主，能量强度分布范围为0～100 Hz，且大部分能量集中于50 Hz 以下的低频段区；而强度高于50 Hz 以上的高频段区瞬时能量散布分量很少。