轴对称指向性球面波的界面反射波*
2022-04-15段韵达胡恒山
段韵达 胡恒山
(哈尔滨工业大学航天科学与力学系,哈尔滨 150001)
无限大平面刚性障板中圆形活塞源的声辐射场可近似为轴对称指向性球面波,前人只给出了活塞面与界面平行时轴对称指向性球面波的界面响应表达式,本文针对活塞面与界面不平行的情况,推导了轴对称指向性球面波的锥面波展开式,并进一步导出了其界面反射波的表达式.在源距远大于声波波长的情况下通过鞍点法将界面反射波的表达式化简为了简化表达式.简化式不仅计算上简洁,而且物理含义清楚:轴对称指向性球面波的界面反射波可视为镜像活塞源激发的轴对称指向性球面波与反射系数的乘积.计算表明,当活塞半径小于声波波长时,反射波对活塞与界面的夹角和接收点的环向方位角不太敏感,反射波的指向性较弱;当活塞半径大于声波波长时,反射波对活塞与界面的夹角和接收点的环向方位角很敏感,反射波的指向性很强.增加活塞与界面的夹角,反射波先增加后减小,反射波的指向性先增强后减弱;当活塞与界面的夹角等于活塞中心镜像点与接收点的连线与界面法线的夹角时,反射波最大,反射波的指向性最强.
1 引言
声波是海洋中探测目标和传递信息的有效工具,而声纳是利用声波获取水下信息的仪器,被广泛用于海洋军事和地质勘探[1,2].声纳的重要组成之一是换能器,换能器类型多种多样,其中复合棒换能器是目前应用最为普遍的换能器之一,由于它产生的是一种类似于活塞式的振动,因而也称为活塞式换能器或纵向换能器[1,3].声源通常嵌入到一坚硬面板中,使声源的辐射场只存在于面板的单侧空间,并使该侧空间内的声辐射场比无面板时更大,此时该面板称为障板[4].障板可以是球形、圆柱或平面,其中平面障板是最基本的障板模型,当声波波长远小于障板尺度时,有限平面障板模型可由无限大平面障板模型描述[5,6].多个活塞安装在障板上形成阵列,可提高声源的发射功率,使声辐射集中于同一方向,更有利于定位水下目标[7].
无限大平面刚性障板中圆形活塞源的声辐射是经典的声辐射模型[8-10],其中活塞面内所有的面元从零时刻开始以相同的速度沿活塞轴线方向振动,障板与活塞面共面,障板在任意时刻都不会发生变形和运动.当活塞中心到接收点的距离远大于活塞半径时,无限大平面刚性障板中圆形活塞(简称为障板活塞)的声辐射场可近似为一种轴对称指向性球面波(轴对称是指波场关于活塞的轴线对称),即[4]
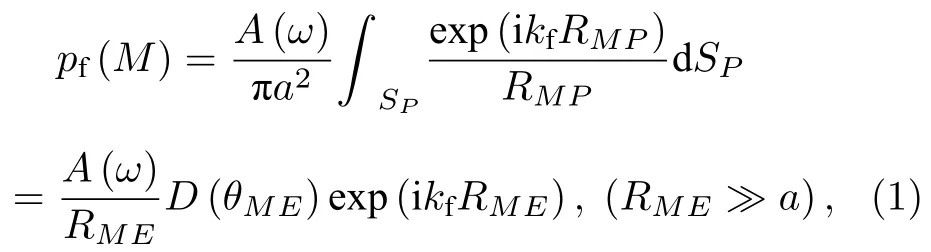
式中第2 个等号的左边为障板活塞源的辐射场,右边为轴对称指向性球面波;pf是流体中的声压(流体可以是水或者空气),a为活塞半径,kf是流体中的声波波数;RMP为接收点M到活塞面上任意点P的距离,SP为圆形活塞面,RME为接收点M到活塞中心E的距离;D(θME) 为指向性函数,有
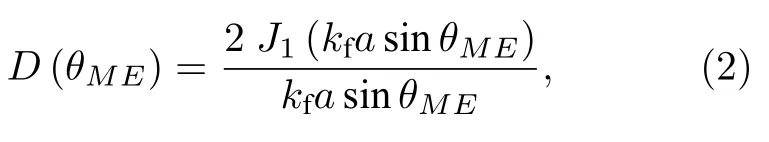
其中J1为一阶第一类贝塞尔函数,θME为接收点M与活塞中心E的连线与活塞轴线的夹角,D(θME)的量纲为1;A(ω) 为声压源的频谱(单位为Pa),有
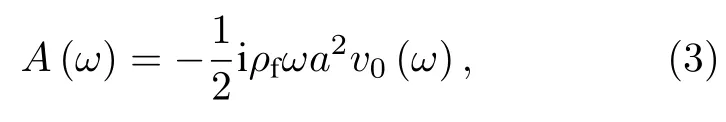
其中v0(ω)为活塞振动速度,ρf为流体密度,ω为角频率,i 为单位虚数.这种轴对称指向性球面波的辐射阻抗和指向特征对指导水下换能器设计[6,11]、水雷探测器设计[12]、隧道微压波计算[13]和医学超声涡旋声场设计[14]有着重要意义.
前面介绍了轴对称指向性球面波在声辐射方面的诸多研究,但轴对称指向性球面波的界面响应却少见报道.Amédin 等[15]针对孔隙介质夹层介于障板活塞与空气之间的情况,推导了障板活塞源的声辐射场对孔隙介质-空气界面的响应表达式,当孔隙介质夹层厚度远大于活塞半径时,该障板活塞源的界面响应式等于轴对称指向性球面波的界面响应式.Wang和Cho[16]考虑了各向异性孔隙介质夹层介于障板活塞与空气之间的情况,当孔隙介质夹层厚度远大于活塞半径时,Wang和Cho 给出的障板活塞源的界面响应式等于轴对称指向性球面波的界面响应式.Schakel 等[17-19]为了检验孔隙介质动电效应理论[20,21]的有效性,推导了指向性球面声波入射流体-孔隙介质界面的响应式.文献[15-19]都是基于人为设计的实验模型给出轴对称指向性球面波的界面响应式,由于实验模型中活塞面与界面平行,所以他们只考虑活塞面与界面平行这一特殊情况,但从理论模型的角度看,活塞面与界面不平行的情况比两者平行的情况更为一般,然而目前未见活塞与界面不平行时轴对称指向性球面波的界面响应式的文献报道.从应用的角度看,海洋地震勘探和水下目标探测时活塞面与界面通常不平行[5,22],在没有理论公式的情况下,虽然可通过数值仿真模拟轴对称指向性球面波的界面反射波,然而当目标界面远离活塞面和接收点时,数值仿真将面临很大的计算量和很长的计算时间,这不利于海底储层和水下目标的探测.因此,本文以轴对称指向性球面波从流体入射固体界面为例,推导活塞面不平行于界面时轴对称指向性球面波的界面反射波的表达式,完善障板活塞源的声辐射场的界面响应理论;推导轴对称指向性球面波的界面反射波的简化表达式,为障板活塞型声源快速探测水下界面提供思路.
2 轴对称指向性球面波的锥面波展开
欲得均匀球面波的界面反射波需先导出均匀球面波的锥面波展开式[23],类似地,欲得轴对称指向性球面波的界面反射波,需先导出轴对称指向性球面波的锥面波展开式.由(1)式知RME ≫a时障板活塞源辐射场近似为轴对称指向性球面波,因而本节从障板活塞源辐射场出发,先导出障板活塞源辐射场的锥面波展开式,再令RME ≫a,则该锥面波展开式近似为轴对称指向性球面波的锥面波展开式.图1 是无限大平面刚性障板中的圆形活塞与界面的示意图,坐标系建立的方式为:从圆形活塞中心E向界面作垂线,交点为O,以EO的连线为z轴,方向向下;使活塞轴线与界面相交,该交点与O点的连线为x轴,方向向右,Oxyz构成右手直角坐标系;使Oxy面与界面重合.活塞中心E到界面的距离为dE,活塞轴线与界面法线的夹角为α,亦即活塞面与界面的夹角为α.本节只考虑入射波的情况,下节再考虑界面反射波的情况.
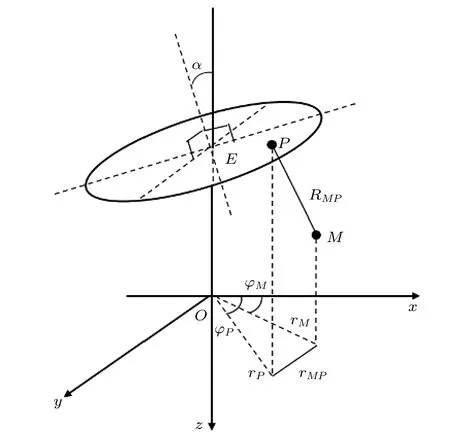
图1 无限大平面刚性障板中的圆形活塞与界面的示意图Fig.1.Schematic diagram of a piston in an infinite plane rigid baffle and an interface.
2.1 障板活塞源辐射场的锥面波展开式
无限大平面刚性障板中圆形活塞的模型如图1所示,图中P是活塞面内的点,M为接收点,由(1)式可知障板活塞源的声压辐射场为[4]
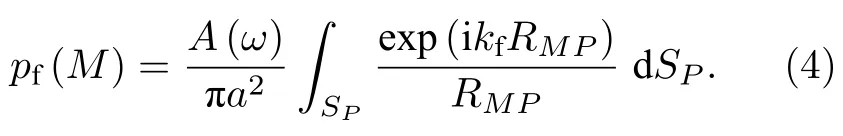
(4)式表明障板活塞源的辐射场可视为活塞面SP内频谱为的点源辐射场在M点处叠加(点源指均匀球面波的点源,下文均为该含义),所以可利用均匀球面波的锥面波展开式处理(4)式.均匀球面波的锥面波展开式为[23]
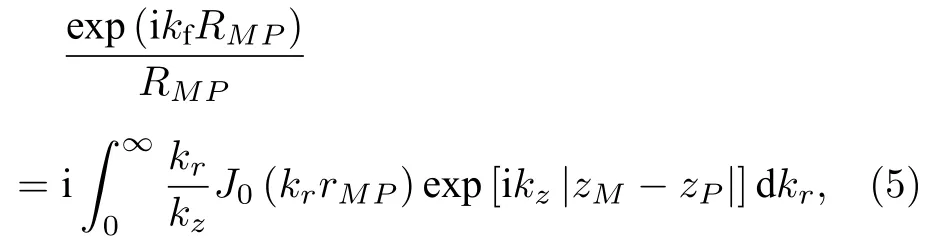
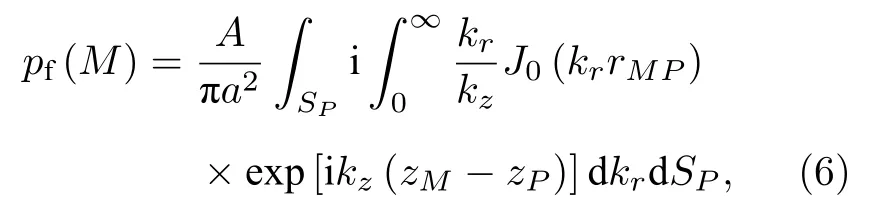
由于径向波数kr及kr积分的上下限均与空间坐标无关,所以可以交换(6)式中的积分次序,得
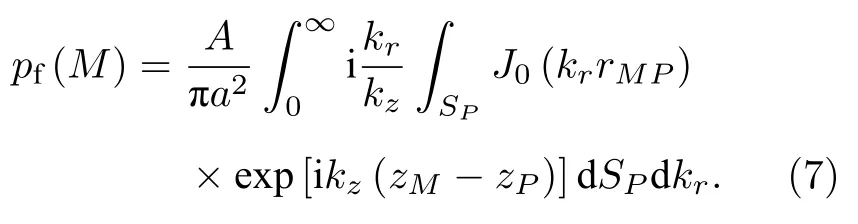
由图1 知,圆形活塞的面元 dSP与其在Oxy面的投影面元 dSF满足
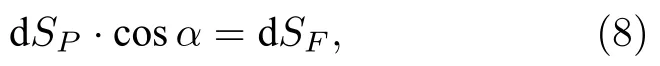
这表明圆形活塞面SP在Oxy面的投影SF是一个椭圆,并且该椭圆的周线方程在直角坐标系和极坐标系下可分别写为
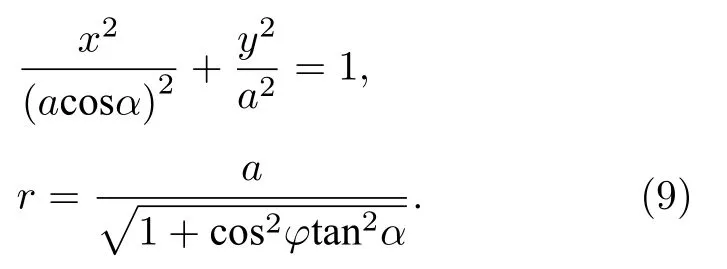
记P点在Oxy面上的投影点为F,由(8)式可知
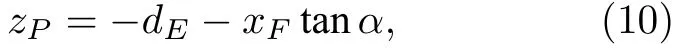
其中dE为活塞中心E到Oxy面的距离,-acosα≤xF≤acosα(因xF位于椭圆SF内).由于P在Oxy面上的投影为F,所以rMPrMF,将rMPrMF,(8)式和(10)式代入(7)式得
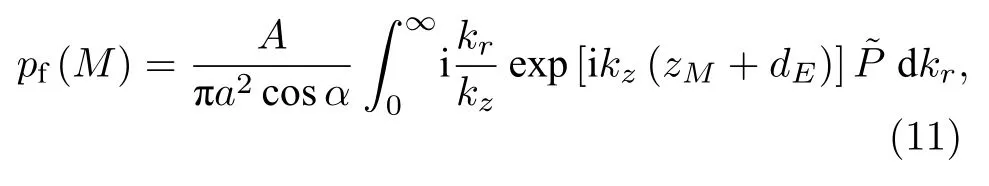
其中
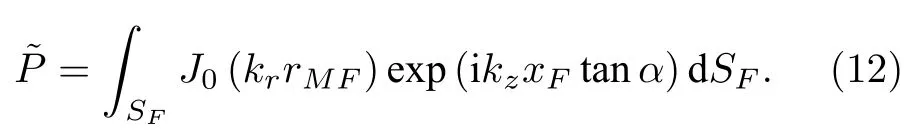
由贝塞尔函数加法定理可得[24]
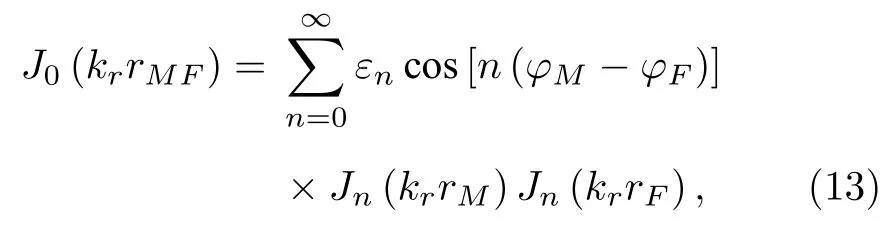
其中εn为纽曼因子,满足ε01,而n≥1时εn2 ;rM和rF分别为M点和F点的径向坐标,φM和φF分别为M点和F点的环向坐标(见图1).将(13)式代入(12)式,并交换积分和求和的次序得
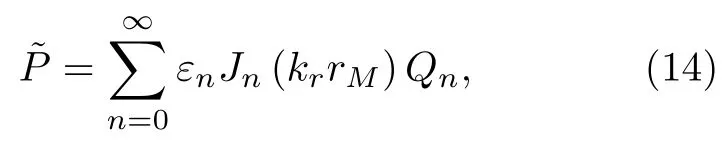
其中
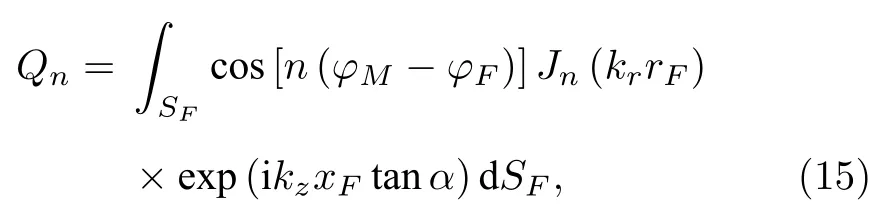
利用三角关系,可将(15)式改写为
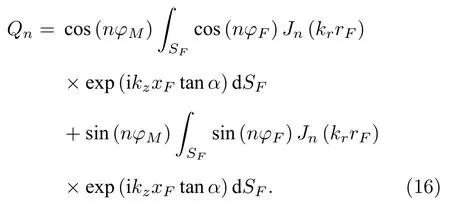
观察(16)式第二行的积分式可知,n≥1 时Jn(krrF)和 exp(ikzxFtanα)均关于φF0对称,而sin(nφF)关于φF0反对称,又椭圆面SF关于φF0 对称(见(9)式),所以n≥1 时(16)式第二行的积分式为零.此外,n0 时 sin(nφF)0,所以综上知n≥0时(16)式第二行的积分项为零,得
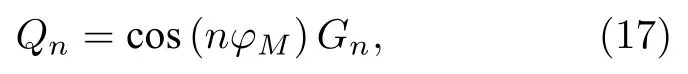
其中
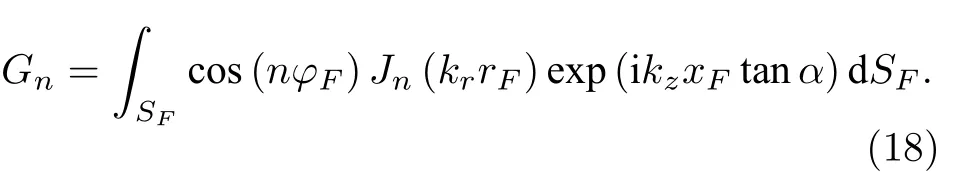
将(17)式和(14)式代入(11)式得障板活塞源辐射场的锥面波展开式
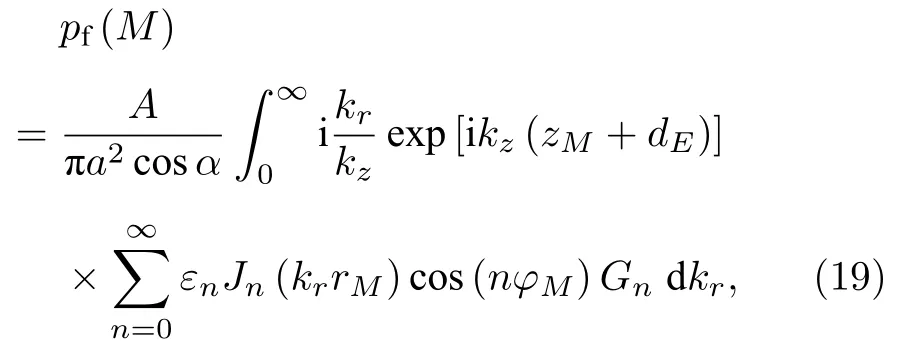
其中Gn由(18)式表达.(19)式表明障板活塞源的辐射场可视为顶点位于z轴zM-dE处的多阶锥面波在M点处的叠加.因(4)式推倒到(19)式的过程中没有用到任何近似条件,而(4)式适用于任意场点[4],所以(19)式也适用于任意场点.
2.2 轴对称指向性球面波的锥面波展开式
由(1)式可知,当活塞中心E到接收点M的距离远大于活塞半径时(RME ≫a),障板活塞源辐射场(4)式近似为轴对称指向性球面波,所以RME ≫a时障板活塞源辐射场的锥面波展开式(19)近似为轴对称指向性球面波的锥面波展开式.RME ≫a时(19)式不仅能用来推导轴对称指向性球面波的界面反射波,也能用来推导界面透射波,本文关注的是界面反射波.
2.3 算例检验
前文看到,RME ≫a时(19)式为轴对称指向性球面波的锥面波展开式,而RME ≫a时(1)式为轴对称指向性球面波(即(1)式中的exp(ikfRME)),所以RME ≫a时(19)式应等于(1)式.因此,这里为了检验(19)式,在RME ≫a的条件下比较(19)式和(1)式.
由轴对称指向性球面波的表达式(1)式和(2)式知,参数kfa控制了障板活塞源的指向能力(kf为流体中声波波长,a为活塞半径),因而本文考虑两类活塞,一类是活塞半径小于声波波长的小活塞,即a<λ,而另一类是活塞半径大于声波波长的大活塞,即a >λ.(19)式中的A为声源频谱,设声源波形为余弦包络脉冲函数,脉冲长度为0.5 ms,中心频率为6 kHz,频率范围为2—10 kHz(高频海洋地震勘探的声源频段[25]),则有λ0.15—0.75 m,所以设小活塞的半径为a0.1 m,大活塞的半径为a1 m .设距离小活塞源1 m 处的声压为 105Pa,距大活塞源1 m 处的声压为 107Pa.对于流体中的入射波而言,只需考虑流体的参数(见表1),设流体的品质因子为100.(19)式和(1)式乘以声源频谱函数可得频域波形,再经傅里叶变换可得时域波形.

表1 流体和固体参数Table 1.Parameters of fluid and solid.
设活塞中心E位于z轴上z-dE-25 m处,活塞面与Oxy面的夹角α30°,接收点M位于 (rM,φM,zM)(21.65,0,-12.5),其中rM,φM和zM的单位分别为米、度和米,则有RME25 m≫1 ≥a,因而RME ≫a条件满足.由M点与E点的位置可知(参考图1),M点位于Oxz面,线段ME与z轴的夹角为 60°,ME与活塞轴线的夹角为 30°,因而M点与O点关于活塞的轴线对称,则M与O点的声压应相等.记锥面波展开式(19)在M点处的计算结果为pf(M),(19)式在O点处的计算结果为pf(O),(1)式在RME25 m且θME30°下的计算结果为pf0.图2 给出了pf(M) ,pf(O)和pf0的计算结果,其中图2(a)和图2(b)分别对应a0.1 m和a1 m,即分别对应小活塞和大活塞.图2(a)和图2(b)表明pf(M),pf(O)和pf0几乎没有区别,因此RME ≫a时轴对称指向性球面波的锥面波展开式(19)与轴对称指向性球面波(1)式一致.
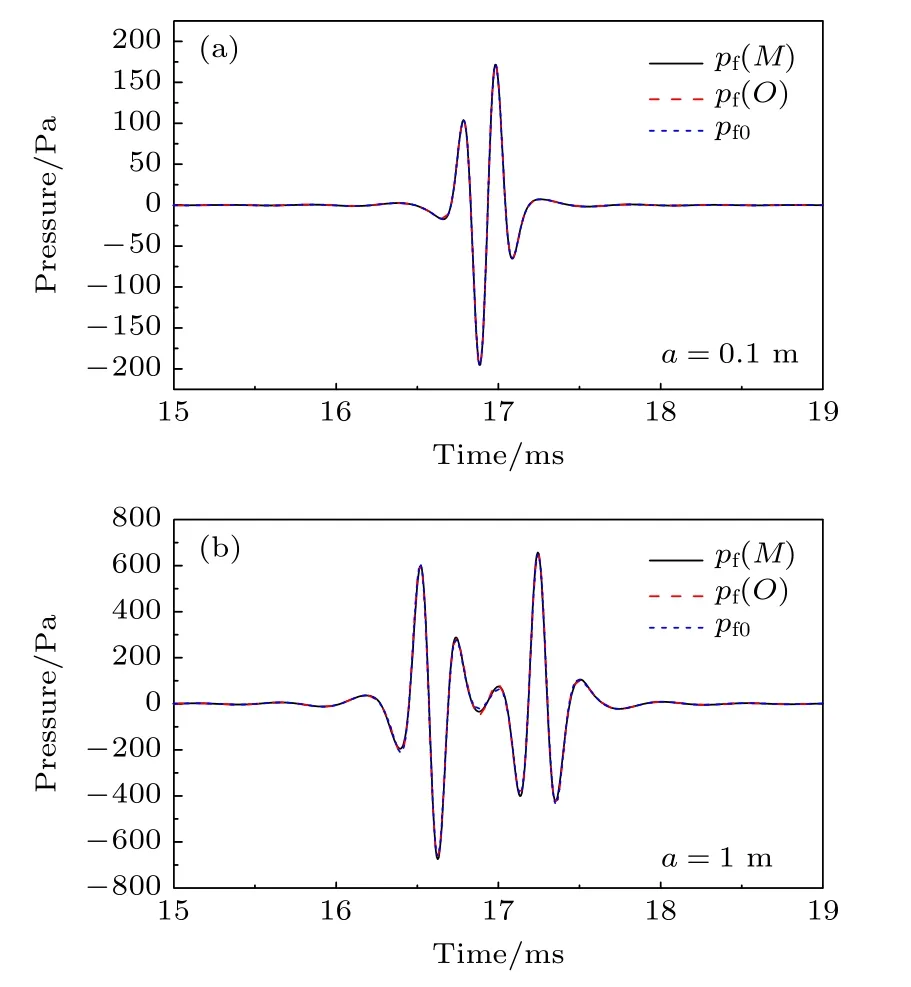
图2 pf(M) ,pf(O) 和 pf0的时域波形 (a) a=0.1 m ;(b)a=1 mFig.2.Time-domain waveforms of pf(M),pf(O)and pf0 :(a) a=0.1 m;(b) a=1 m .
3 轴对称指向性球面波的界面反射波的表达式
前文表明RME ≫a时障板活塞源辐射场的锥面波展开式(19)近似为轴对称指向性球面波的锥面波展开式,由此可知RME ≫a时障板活塞源辐射场的界面反射波表达式近似为轴对称指向性球面波的界面反射波表达式,因此本节先推导障板活塞源辐射场的界面反射波表达式,再令RME ≫a即得轴对称指向性球面波的界面反射波表达式.图3 给出了活塞面关于界面的镜像,图中活塞SP1为活塞SP的镜像,E1为E的镜像,P1为P的镜像,M为反射波的接收点,M2为M在Oxy面上的投影点.
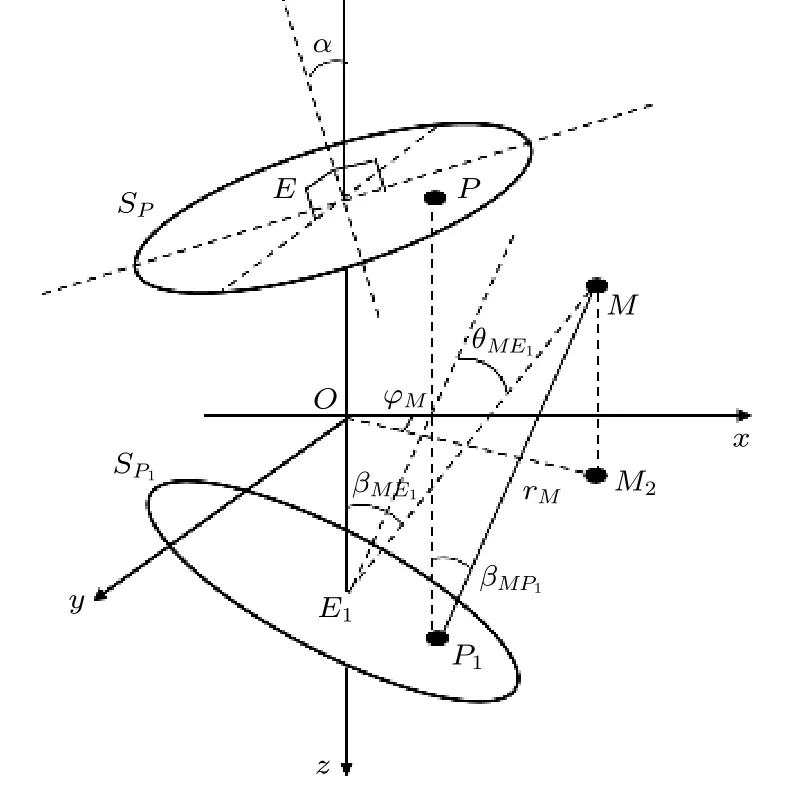
图3 活塞面关于界面的镜像Fig.3.Mirror image of the piston surface with respect to the interface.
参考锥面波展开式(19)的形式,设障板活塞源辐射场的界面反射波为
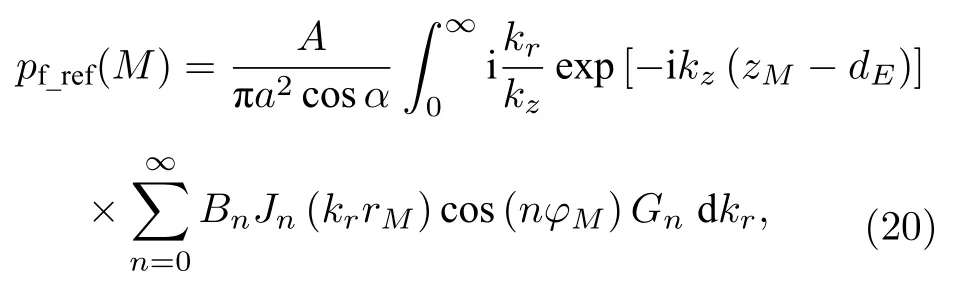
其中M点为反射波的接收点,BnBn(kr) 为待定系数,需通过边界条件确定,具体过程为:参考(19)式的形式先列出透射纵波和横波的表达式,再将它们和(20)式代入流体-固体界面边界连续条件可得Bn满足的线性方程组,最后求解该线性方程组即得Bn.然而,我们并不打算通过上述方式求解Bn以获得界面反射波的表达,因为由(1)式注意到障板活塞源的辐射场等于活塞面SP上点源辐射场的叠加,则障板活塞源辐射场的界面反射波等于活塞面SP上点源辐射场的界面反射波的叠加.对于活塞面SP上的单个点源P而言,其界面反射波为[23]
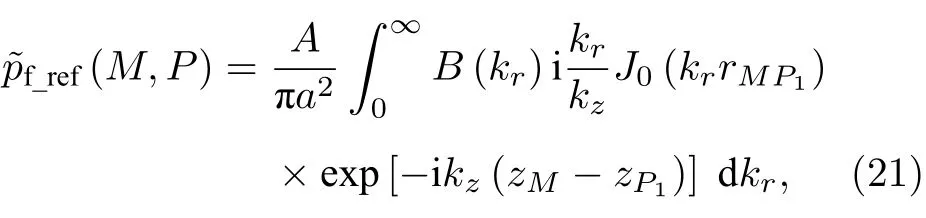
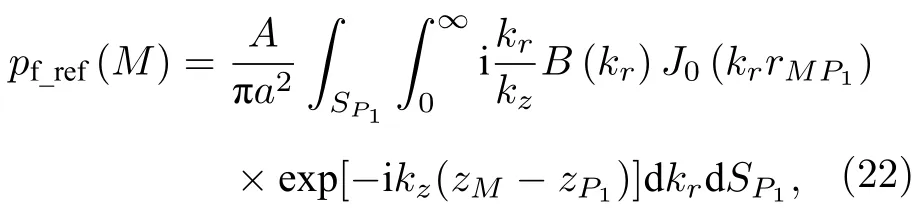
由于径向波数kr及kr的积分上下限均与空间坐标无关,所以可以交换(22)式中的积分次序,得
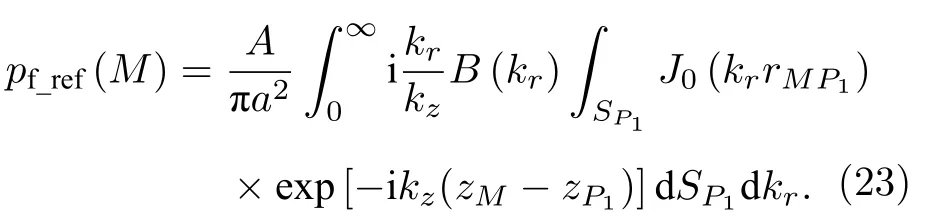
由于P1为P的镜像,所以由(10)式得
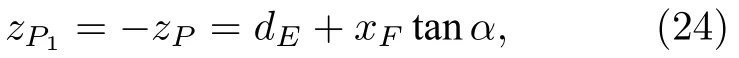
由 于SP在Oxy面的投影为SF,而SP和关 于Oxy面对称,所以SP1面在Oxy面的投影也是SF(参照图3),则有·cosαdSF和rMF,再将这两式代入(23)式得
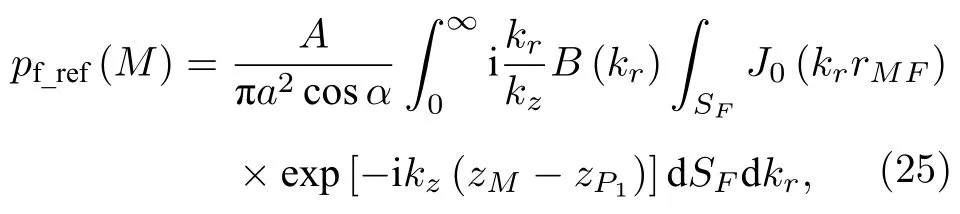
将(24)式代入(25)式得
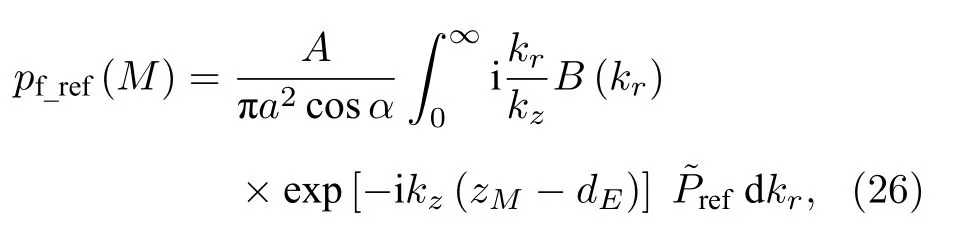
其中
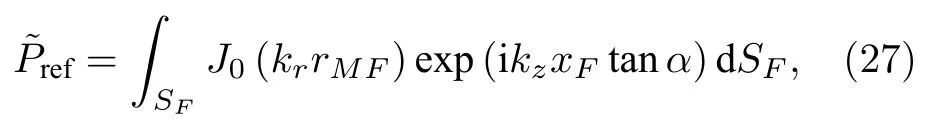
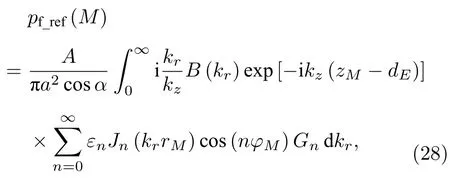
其中Gn由(18)式表达;εn为纽曼因子,满足ε01,而n≥1时εn2 .至此,我们导出了活塞面与界面不平行时障板活塞源的界面反射波表达式(28)式,令≫a则(28)式近似为活塞面与界面不平行时轴对称指向性球面波的界面反射波表达式,相比前人只考虑活塞面与界面平行的情况而言[15-19],(28)式完善了轴对称指向性球面波的界面响应理论.比较(28)式和(20)式可知BnεnB(kr),而B(kr)已由前人给出[23],所以无需求解Bn满足的线性方程组,通过点源叠加的方式就可以获得轴对称指向性球面波的界面反射波.此外,前文的算例表明RME ≫a时轴对称指向性球面波的锥面波展开式(19)正确,而这里从(19)式到(28)式的过程中用的都是恒等式,因而RME ≫a时轴对称指向性球面波的界面反射波(28)式也正确,从而无需再通过算例检验(28)式.
4 轴对称指向性球面波的界面反射波的简化表达式
当活塞半径远小于声波波长 (a ≪λ) 时有kfa ≪1,代入(2)式得D(θME)→1,即指向性函数几乎不随M点的方位改变,则由(1)式知轴对称指向性球面波退化为均匀球面波,从而其界面反射波退化为均匀面波的界面反射波,因此a ≪λ的情况无需研究,而对于a不远小于λ的一般情况,本文研究轴对称指向性球面波的界面反射波的简化表达式.海洋地震勘探[25]和水下目标超声探测[26,27]时,活塞中心E关于界面的镜像E1到接收点M的距离通常远大于声波波长(≫λ),则鞍点法的使用条件≫1 得到满足,从而可用鞍点法化简轴对称指向性球面波的界面反射波的表达式(28).
4.1 基于鞍点法的简化表达式
由图3 可知 (zM -dE)-|zM -dE|,将其代入(28)式,再将n写为偶数和奇数阶的形式得
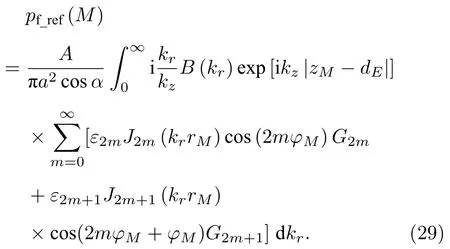
由贝塞尔函数教材可知[28]J2m(x)J2m(-x)和J2m+1(x)-J2m+1(-x),其中m0,1,2,3,···,再代入(18)式得
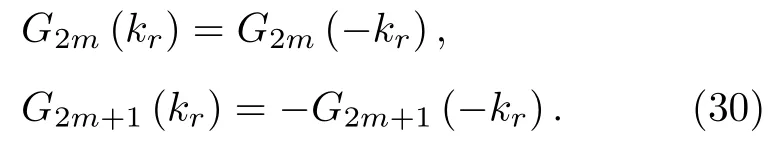
由贝塞尔函数教材可知[28]
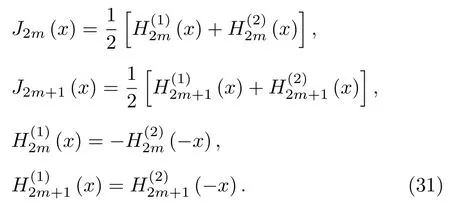
利用(30)式和(31)式,并考虑到kz和B(kr) 是关于kr的偶函数[23],则(29)式可改写为
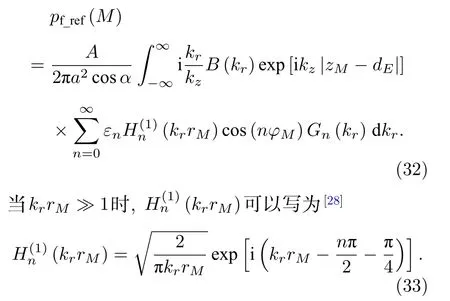
再将(33)式代入(32)式得
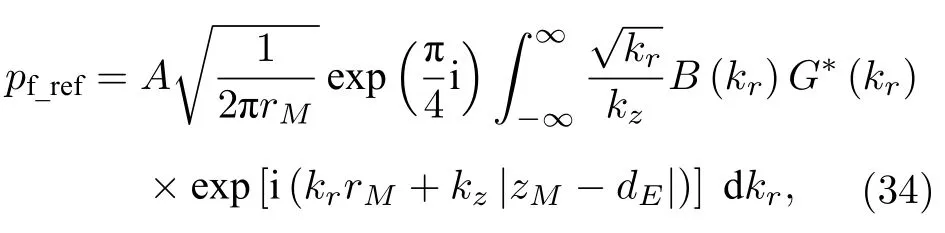
其中
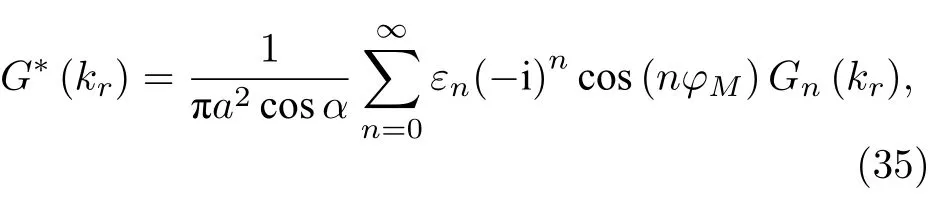
其中Gn(kr) 由(18)式表达.由附录A 可知,最速下降路径和鞍点是由e 指数函数中的宗量决定,因而需确定(34)式中所有的e 指数函数.(34)式中B(kr)是平面波的反射系数,不是e 指数函数[23],而G*(kr) 也不是e 指数函数(见附录B),因此(34)式中只有 exp[i(krrM+kz|zM -dE|)] 是e 指数函数,则(34)式可改写为

由图3 知M2是M在Oxy面的投影,E1是E在Oxy面的投影,则MM2与OE1平行,OM2垂直于OE1,又rM,所以
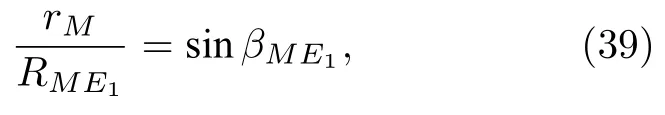
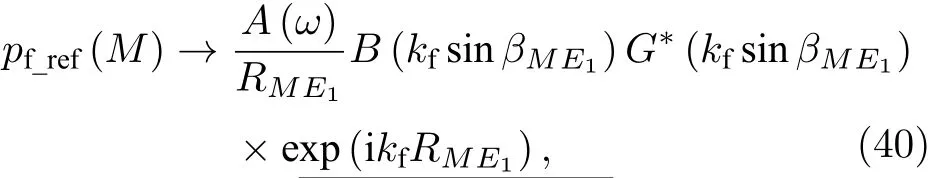

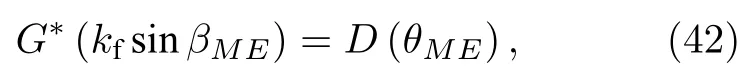
其中θME为M与E的连线与活塞SP轴线的夹角.由(42)式可得
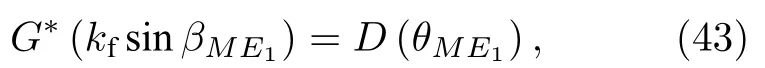

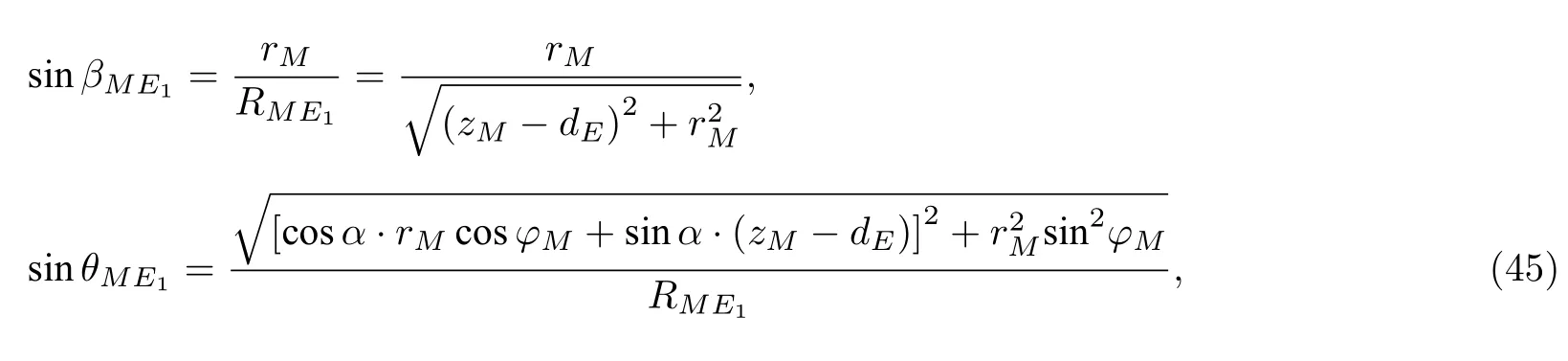
其中 (rM,φM,zM) 为M点的柱坐标(见图3).比较反射波简化式(44)和入射波(1)式可知,轴对称指向性球面波的反射波可视为镜像源的波乘以反射系数B,其中镜像源的波指镜像活塞面激发的轴对称指向性球面波.因此简化式(44)的物理含义比(28)式更为清楚.此外,与(28)式相比,简化式(44)无需计算贝塞尔函数在椭圆面上积分、不同阶锥面波的求和及波数域的积分,所以简化式(44)省去了巨大的计算量,减少了大量计算时间.另外,需要说明的是,(1)式表明当活塞中心到接收点的距离远大于活塞半径时(RME ≫a),障板活塞源辐射场近似为轴对称指向性球面波,所以我们考虑轴对称指向性球面波时应默认RME ≫a成立,从而考虑其界面反射波时有≫a成立.因此简化式(44)的成立条件是≫a和≫1同时成立,其中≫1 是鞍点法的使用条件,而≫a是默认成立的条件.
值得一提的是,简化式(44)也可用另一种更为简单的方式导出.因考虑轴对称指向性球面波的界面反射波时默认≫a成立,则由≫1条件可导出≫1,即对于活塞面上任意一点P鞍点法的使用条件成立,所以可通过鞍点法将活塞面SP上单个点源P的辐射场的界面反射波(21)式化简为[23]
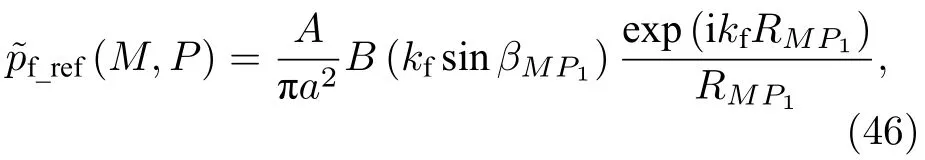
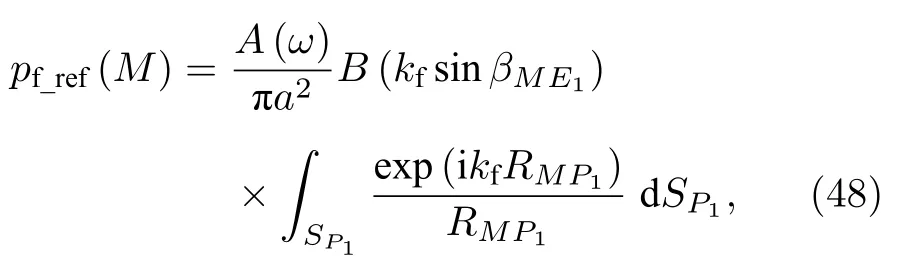
再利用(1)式可得
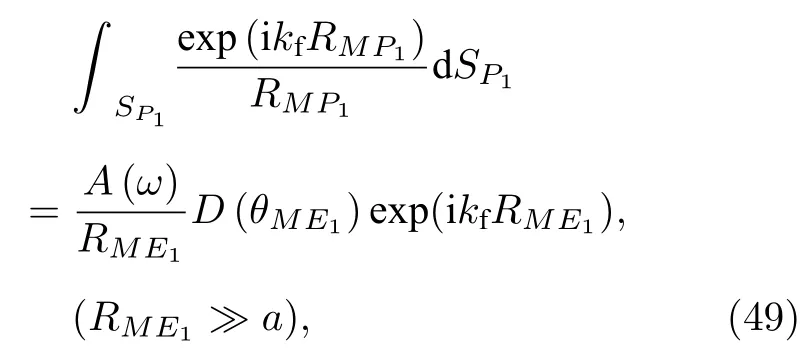
最后将(49)式代入(48)式即得简化式(44).
4.2 算例检验
本节通过算例检验简化式(44)的正确性,即比较(44)式和(28)式的一致性.声源设定与前文算例相同,流体和固体参数见表1,地层纵波和横波的品质因子分别为80和60,流体中声波的品质因子为 100 .
参照图3,设活塞面SP与界面Oxy的夹角为α30°,活塞中心E与界面的距离为dE5 m,则E点位于z轴上z-dE-5 m 处;设接收点M的位置为,其中rM,φM和zM的单位分别为米(m)、度(°)和米(m),此后默认为该单位.由M点和E1点的坐标可知20 m≫1 m,而小活塞和大活塞的半径分别为a0.1 m和a1 m,所以有≫a;由于流体中声波波长为λ0.15—0.75 m,则/λ≥26.7 m≫1 m,所以鞍点法的使用条件≫1成立.综上可得≫a和≫1 成立,则简化式(44)可以用来计算轴对称指向性球面波的界面反射波.
记(28)式和简化式(44)计算幅度谱分别为Pref和Pref_jian.图4 为Pref与Pref_jian的比较,其中图4(a)对应a0.1 m 时快速地层,图4(b)对应a0.1 m时慢速地层,图4(c)对应a1 m 时快速地层,图4(d)对应a1 m 时慢速地层.图4(a)—图4(d)表明,无论快速地层还是慢速地层,无论小活塞还是大活塞,均有Pref_jian与Pref一致,因此简化式(44)与(28)式一致,即简化式(44)正确.另外,因简化式(44)是通过鞍点法导出的,所以鞍点法的使用条件≫1 决定了简化式(44)的适用范围.上述算例中声源频率为高频海洋地震勘探频率(2—10 kHz),并且有20 m,所以简化式(44)适用于≥20 m 的高频海洋地震勘探问题,由于活塞中心E距地层界面 10 m 以上还是容易满足的,所以简化式(44)有着较为广泛的适用范围.另外,超声频率下(f > 20 kHz),≥1 m 时简化式(44)也是适用的,但这里不再给出具体算例.
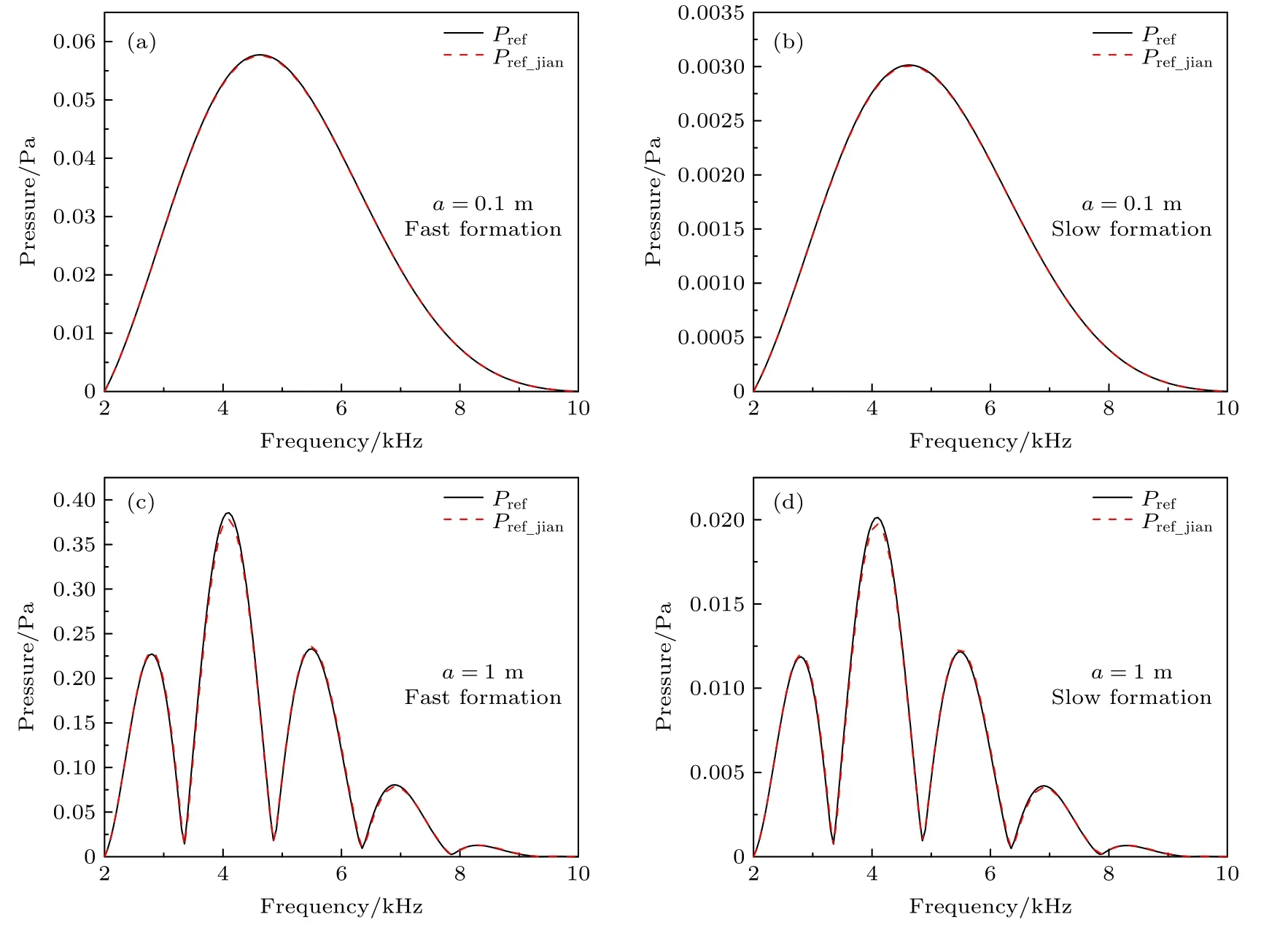
图4 Pref与 Pref_jian的比较 (a) a=0.1 m且快速地层;(b) a=0.1 m且慢速地层;(c) a=1 m且快速地层;(d) a=1 m 且慢速地层Fig.4.Comparison of Prefand Pref_jian:(a) a=0.1 mand fast formation;(b) a=0.1 mand slow formation;(c) a=1 m and fast formation;(d) a=1 m and slow formation.
5 位置参数对界面反射波的影响
本节基于简化式(44),研究活塞面与界面的夹角α、接收点M的环向方位角φM和线段ME1与界面法线的夹角对轴对称指向性球面波的界面反射波的影响,其中接收点M的位置由柱坐标(rM,φM,zM)描述(见图3),活塞中心E位于(0,0,-dE),则活塞中心镜像E1位于 (0,0,dE) .由于活塞源嵌入无限大障板中,所以障板背面不存在活塞源的辐射场,例如当活塞与界面的夹角为α90°时,由图3 可知源的辐射场(即入射波)只存在于x≥0的半空间,而当α0°时源的辐射场只存在于z≥-dE的半空间;因此对于α0°—90°的活塞源而言,设界面反射波的接收点M位于x≥0 且-dE≤z≤0的空间.声源设定与第4 节一致,流体和固体地层参数见表1,流体中声波品质因子为100,固体中纵波和横波的品质因子分别为80和60.
5.1 活塞与界面的夹角的影响
记过活塞轴线且与界面垂直的面为η面,则φM0°时M位于η面,φM90°时M位于与η面垂直的面.设活塞中心E位于z轴上z-dE-10 m处,反射波接收点M位于(rM,φM,zM)0,-10),其中rM,φM和zM的单位分别为米(m)、度(°)和米(m),此后默认为该单位.参考图3 可知,M位于η面,并且βME1∠ME1O60°.地层取为快速地层,见表1.图5 给出了不同夹角α下在M点处的反射波,其中图5(a)和图5(b)分别对应a0.1 m和a1 m .由图5(a)可知,小活塞源(a<λ)的辐射场的界面反射波随α变化不大,波形随α增加出现先增后减的现象,并且与活塞面和界面平行时(α0°)的结果相差不大.由图5(b)可知,大活塞源 (a >λ) 的辐射场的界面反射波随α显著改变,波形随着α的增加出现先增后减的现象,并且α30°和α90°下的波形相等.慢速地层下的结果类似,结论同上.接下来对图5 的结果做出解释,由于a<λ时入射波的指向性函数D随θ的改变不太敏感,所以小活塞源的辐射场的指向性较弱,因而其界面反射波随α的改变不大(见图5(a)),而a >λ时情况相反(见图5(b)).(44)式表明轴对称指向性球面波的界面反射波可以视为镜像活塞源激发的波(下文简称镜像源的波)与反射系数B的乘积,由于图5 中变化的位置参数只有α,则由(45)式和(2)式可知镜像源的波受影响,而反射系数B不受影响,所以镜像源的波随α的变化规律即界面反射波随α的变化规律.对于图5 而言,α60°时镜像活塞轴线经过M点,得(见图3),则D取得最大值1,此时M点处镜像源的波取得最大值;由于图5中不变,则从 0°开始增加α直至 90°的过程中,镜像活塞轴线先接近M点再远离M点,所以M点处镜像源的波先增大后减小.因此,由镜像源的波随α的变化规律可知,图5 中界面反射波随α的增加而先增大后减小,并且在α60°处取得最大值.此外,图5 中α30°和α90°下的镜像活塞轴线关于ME1对称,则α30°和α90°下的界面反射波也关于ME1对称,又因M点接收的是声压,所以图5 中α30°和α90°下的界面反射波相等.
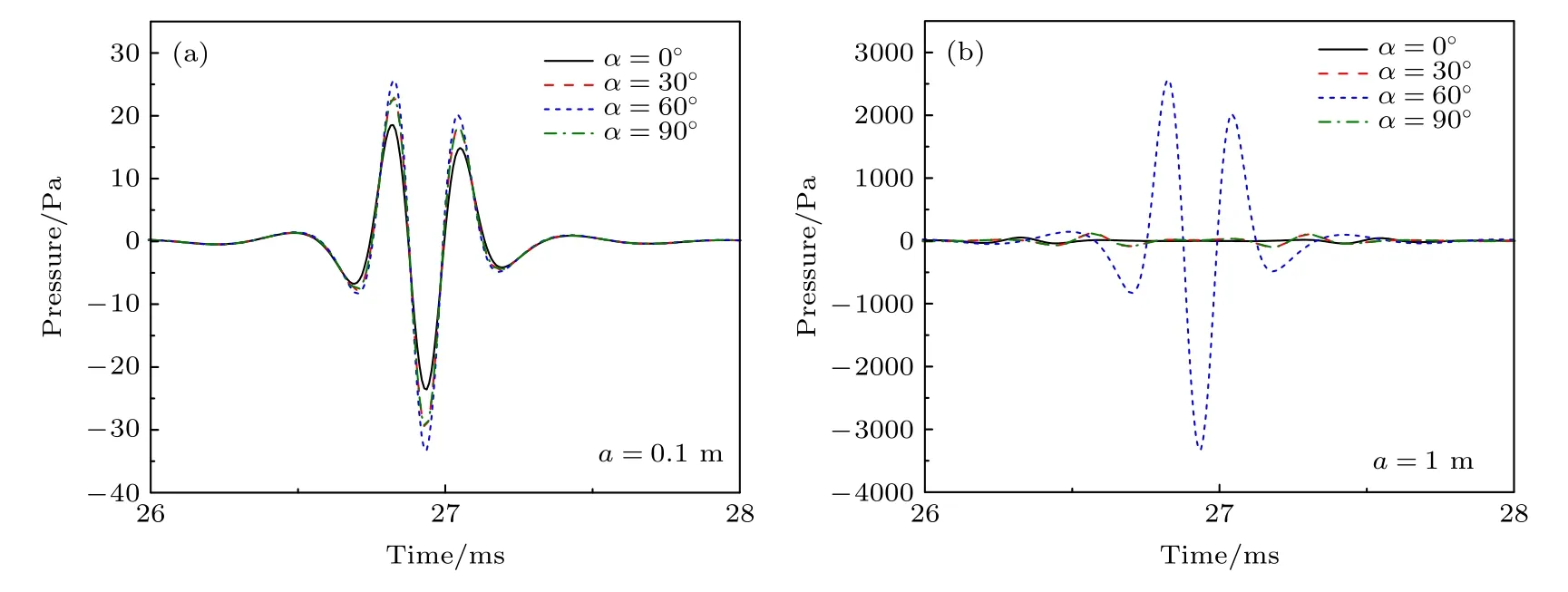
图5 不同夹角α下在M 点(200,-10)处的反射波(a)a=0.1m;(b)a=1 mFig.5.Reflected wave under different included angleαfor pointMat (200,-10):(a)a=0.1 m;(b) a=1 m .
前面算例表明,在给定M点 (rM,φM,zM)和E1点 (0,0,dE) 的情况下,改变α则镜像活塞的轴线与M点的距离d改变,又因不随α改变,所以最小的d值对应镜像源的波最大(见(44)式、(45)式和(2)式).因此,需要找到使d最小的α值,从而判断镜像源的波随α的变化规律,继而判断界面反射波随α的变化规律.由图3 知镜像活塞的轴线与M点的距离d等于,则由(45)式知
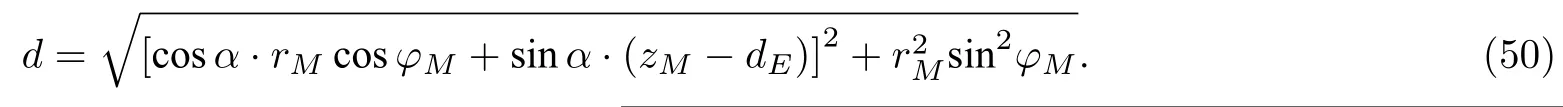
在给定M点 (rM,φM,zM)和E1点 (0,0,dE) 的情况下,求d的导数零点(d对α的导数)可得
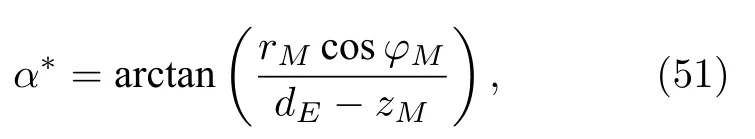
由于d的二阶导数在αα*处大于零,所以αα*时镜像活塞轴线与M点的距离d最小,此时M点处镜像源的波最大.由于反射系数不随α改变,则镜像源的波随α的变化规律即界面反射波随α的变化规律,所以αα*时M点处的界面反射波最大.因此 0°≤α<α*时界面反射随α增加而增大,α*≤α≤90°时界面反射随α增加而减小.
图6 给出了不同夹角α下在M点45,-10)处(此时M点离开η面)的反射波,其中图6(a)和图6(b)分别对应a0.1 m和a1 m .由图6(a)可知,小活塞源 (a<λ) 的辐射场的界面反射波随α变化较小,与活塞面和界面平行时(α0°)的结果相差较小.由图6(b)可知大活塞源 (a >λ) 的辐射场的界面反射波随α改变明显,波形随着α的增加出现先增后减的现象.慢速地层下的结果类似,结论同上.图7 给出了不同夹角α下在M点90,-10)处(此时M点位于与η面垂直的平面)的反射波,其中图7(a)和图7(b)分别对应a0.1 m和a1 m .由图7(a)可知,小活塞源 (a<λ) 的辐射场的界面反射波几乎不随α变化,与活塞面和界面平行时(α0°)的结果几乎没有差别.由图7(b)可知大活塞源 (a >λ) 的辐射场的界面反射波随α改变较为明显,波形随着α的增加而减小,不同于图6 中波形随着α的增加而先增后减.慢速地层下的结果类似,结论同上.接下来对上述结果做出解释,由(51)式知图6 对应α*50.8°,则界面反射波在αα*50.8°处最大,所以波形随α的增加而先增后减;由(51)式知图7对应α*0°,则界面反射波在αα*0°处最大,所以波形随α增加而减小.
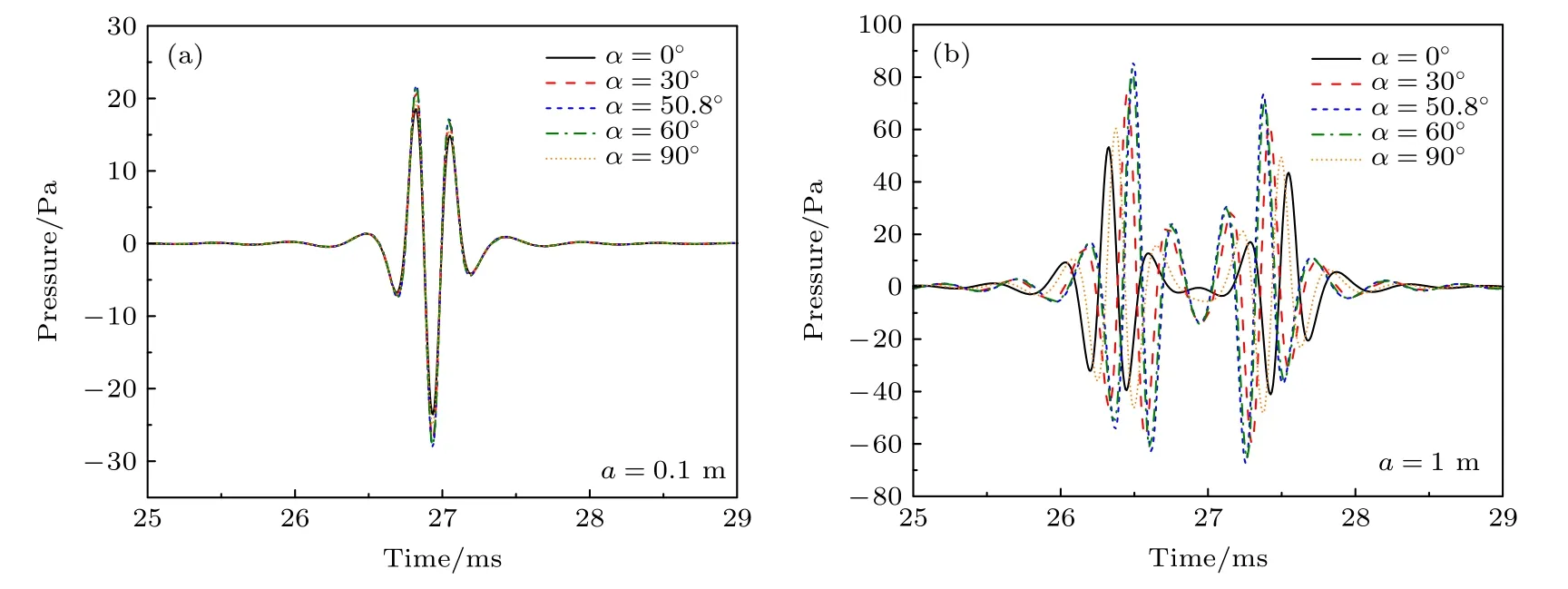
图6 不同夹角α下在M点45,-10)处的反射波(a)a=0.1m;(b)a=1 mFig.6.Reflected wave under different included angleαfor point M at 45,-10):(a) a=0.1 m;(b) a=1 m .
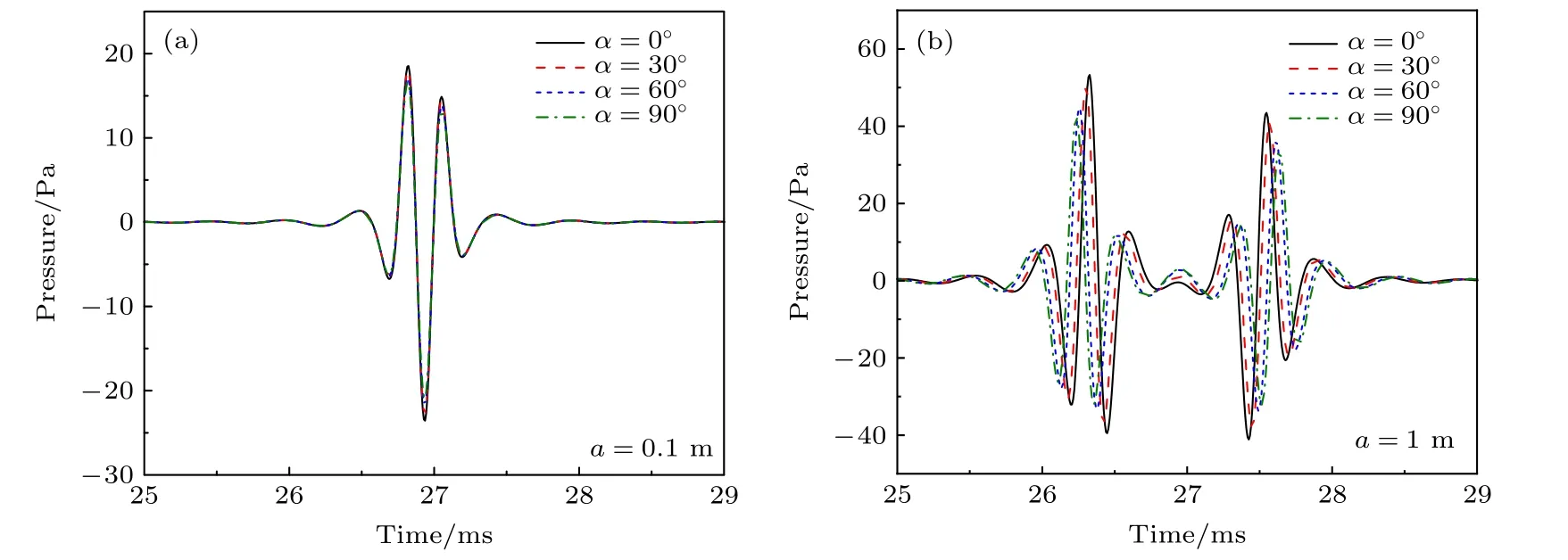
图7 不同夹角α 下在M 点 90,-10)处的反射波 (a) a=0.1 m;(b)a=1 mFig.7.Reflected wave under different included angle α for point M at 90,-10):(a) a=0.1 m;(b) a=1 m.
5.2 接收点的环向方位角的影响
由于障板背面无辐射场存在,则有意义的方位角范围为φM-90°—90°.由图3 知活塞和界面均关于Oxz面对称,又M点接收的是流体中的声压,所以φM0°—90°范围的界面反射波与φM-90°—0°范围的界面反射波对称且相等.设活塞中心E位于 (0,0,-10),则E的镜像E1位于 (0,0,10),设接收点M的位置为φM,-10),得40 m和60°,并且和不随φM改变.地层取为快速地层,见表1.
图8 给出了α45°时不同φM下的界面反射波和其指向图,其中指向图是向φM0°处的波形的最大幅度归一,图8(a)对应a0.1 m 时的反射波,图8(b)对应a0.1 m 时的指向图,图8(c)对应a1 m时的反射波,图8(d)对应a1 m 时的指向图.由图8(a)和图8(c)可知,反射波在φM0°处最大,并且随着φM的增加而减小.因不随φM改变,则反射系数也不随φM改变(见(45)式),所以镜像源的波随φM的变化规律决定了反射波随φM的变化规律;由于镜像活塞的轴线位于φ0°面(即Oxz面,见图3),且不变,则增加φM导致M点与镜像活塞轴线的距离增加,所以镜像源的波减小,因而反射波在φM0°处最大,并且随φM的增加而减小.另外,比较图8(a)和图8(c)可知,小活塞情况下反射波随φM的增加缓慢减小,而大活塞情况下反射波随φM的增加迅速减小,所以大活塞情况下反射波对φM更为敏感.此外,比较图8(b)和图8(d)可知,大活塞情况下的反射波的指向性强于小活塞,这是因为在反射系数不变的情况下,镜像活塞源的辐射场的指向性决定了反射波的指向性,而由(2)式可知大活塞源的辐射场的指向性强于小活塞源,那么其反射波的指向性也强于小活塞.
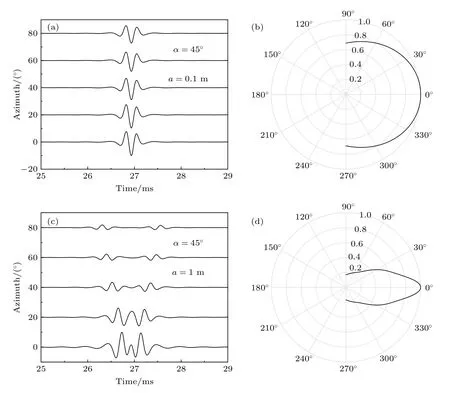
图8 α=45°时不同 φM下的反射波和其指向图 (a) a=0.1 m时的反射波;(b) a=0.1 m时的指向图;(c) a=1 m 时的反射波;(d) a=1 m 时的指向图Fig.8.Reflected waves and directional diagrams at different azimuths φMfor α=45°:(a) Reflected waves for a=0.1 m ;(b) directional diagram for a=0.1 m;(c) reflected waves for a=1 m;(d) directional diagram for a=1 m .
图9 给出了不同α下的反射波的指向图,其中图9(a)和图9(b)分别对应a0.1 m和a1 m .由图9(a)和图9(b)可知有两个特征存在:小活塞情况下反射波的指向性对α的改变不太敏感,而大活塞情况下反射波的指向性对α的改变很敏感;反射波的指向性随α的增加出现先增后减的现象.第一个特征的出现是因为α的改变不影响反射系数,则镜像活塞源的辐射场的指向性决定了反射波的指向性,由于镜像小活塞源的指向性较弱,所以反射波的指向性对α的改变不太敏感,由于镜像大活塞源的指向性强,所以反射波的指向性对α的改变很敏感.第二个特征的出现是因为且φM0°时镜像活塞的轴线通过M点,对应镜像源的波最大,又60°(由M点E1点的位置确定,但不随φM改变),则α60°且φM0°时的镜像源的波最大,所以在α60°下从φM0°开始增加或减小φM将导致镜像源的波剧烈变化,因而α60°下反射波的指向性最强,则反射波的指向性随α的增加出现先增后减的现象.

图9 不同夹角α 下的反射波的指向图 (a) a=0.1 m;(b)a=1 mFig.9.Directional diagrams under different angle α:(a) a=0.1 m;(b) a=1 m .
5.3 线段ME1 与界面法线的夹角的影响
线段ME1与界面法线的夹角即,设活塞中心E位于z轴上z-dE-10 m 处,当M点位于 (7.279,φM,-10)时有20°,而当M点位于 (16.782,φM,-10)时有40°.图10 给出了a1 m 时不同α下的反射波的指向图,其中图10(a)和图10(b)分别对应20°和40°.图10(a)表明反射波的指向性随着α的增加而先增后减,在α20°处达到最大值;图10(b)表明反射波的指向性随着α的增加而先增后减,在α40°处达到最大值;因此,界面反射波的指向性随着α的增加而先增后减,在α处达到最大值.

图10 a=1 m时不同夹角α 下的指向图 (a) =20°;(b)=40°Fig.10.Directional diagrams under different angle α for a=1 m:(a)=20°;(b) =40° .
由(44)式和(45)式可知,βME1直接影响反射系数B,所以在给定镜像源的波和地层参数的情况下,决定了界面反射波的大小.图11 给出了反射系数的绝对值|B|随的变化曲线(B的量纲为1),可以看出,快速地层下的反射系数大于慢速地层下的反射系数,因而快速地层下的界面反射波总是大于慢速地层,而图4 恰好说明了这一点.
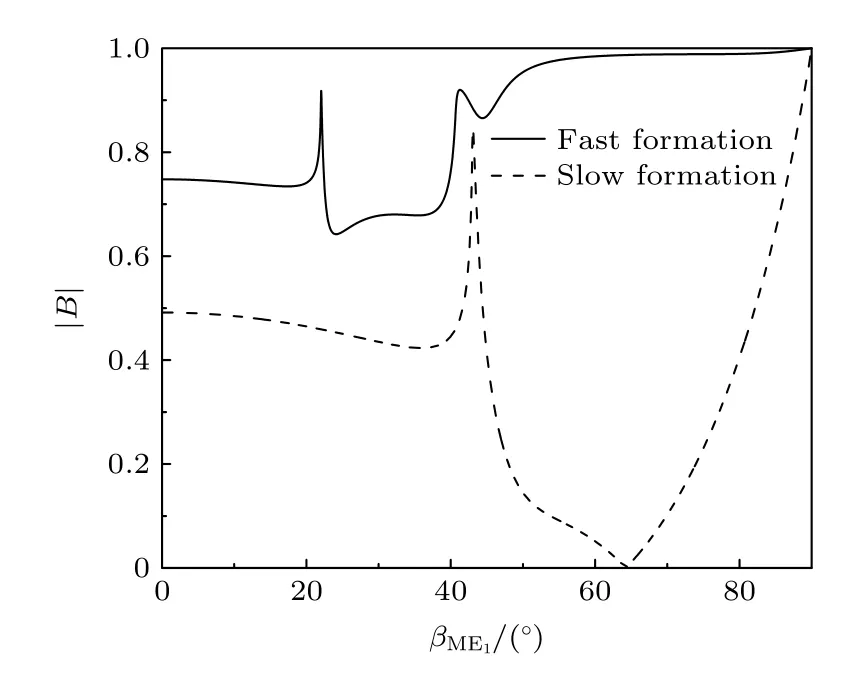
图11 |B| 随的变化曲线Fig.11.Variation curve of|B|with .
另外,由(44)式可知,轴对称指向性球面波的反射波中含有项,所以反射波的到时td等于镜像活塞中心到接收点的距离除以流体中声速vf,即td其中zM和rM分别为接收点的轴向和径向坐标.因此,利用反射波的到时td可推算活塞源与界面的距离dE,而图5—图7 中反射波的到时都符合td的上述表达式.
6 结论
本文导出了无限大平面刚性障板中圆形活塞源(简称障板活塞源)辐射场的锥面波展开式(19),该式由多阶锥面波构成,适用于任意场点.前人在活塞中心到接收点的距离远大于活塞半径的条件下,将障板活塞源辐射场近似为轴对称指向性球面波(1)式,而本文算例表明该条件下障板活塞源辐射场的锥面波展开式(19)近似为轴对称指向性球面波的锥面波展开式.利用(19)式导出了活塞面与界面呈任意夹角时障板活塞源辐射场的界面反射波(28)式,并且当活塞中心的镜像点到接收点的距离远大活塞半径时,(28)式近似为轴对称指向性球面波的界面反射波表达式.(28)式相比前人只考虑活塞面与界面平行的情况而言,完善了无限大平面刚性障板中圆形活塞源的界面响应理论.
海洋地震勘探和水下目标超声探测中,活塞中心的镜像点到接收点的距离通常远大于声波波长,从而鞍点法的使用条件得到满足.本文利用鞍点法和(1)式将轴对称指向性球面波的反射波(28)式化简为了(44)式.简化式(44)适用于活塞中心的镜像点到接收点的距离同时远大于声波波长和活塞半径的情况.简化式(44)数学形式简洁,物理含义清楚,即轴对称指向性球面波的反射波等于镜像活塞源激发的轴对称指向性球面波与反射系数的乘积.
本文基于简化式(44),通过数值算例研究了活塞面与界面的夹角α、接收点M的环向方位角φM和线段ME1与界面法线的夹角对轴对称指向性球面波的界面反射波的影响.当活塞半径小于流体中声波波长时(a<λ),反射波对α不太敏感,当活塞半径大于流体中声波波长时(a >λ),反射波对α很敏感.增加活塞与界面的夹角α,反射波先增加后减小,而且α时取得最大值.因障板背面无波场存在,则接收点M有意义的方位角范围为φM-90°—90°,又反射波场关于φM0°平面对称,且M点接收的是声压,所以φM0°—90°与φM-90°—0°的反射波对称且相等.在φM-90°—90°上,反射波随方位角φM的增加而先增后减,在φM0°处取得最大值.a<λ时反射波对φM不太敏感,反射波的指向性较弱,a >λ时反射波对φM很敏感,反射波的指向性很强(相比a<λ而言).a<λ时反射波的指向性对α不太敏感,a >λ时反射波的指向性对α很敏感;增加活塞与界面的夹角α,反射波的指向性先增强后减小,当α时反射波的指向性最强.直接影响反射系数,0°—90°时快速度地层的反射系数大于慢速地层的反射系数,因而快速地层下的反射波大于慢速地层下的反射波.
附录A 鞍点法
这里给出鞍点法的简要介绍[23].对于积分式
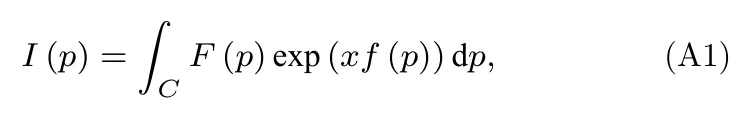
其中F(p) 和f(p) 是关于复数p的解析函数,x是正实数,C是积分路径(通常为实轴积分路径).当x是足够大的正实数时,I(p)的值由 exp(xRef(p)) 控制,若将积分路径C变换为最速下降路径(即 Imf(p)=const 且经过鞍点,而鞍点满足f′(pan)=0),则I(p) 主要由鞍点附近的最速下降路径积分决定,并可以写为
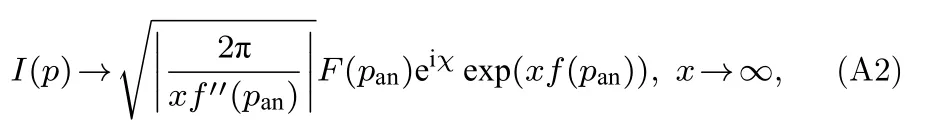
其中χ是鞍点附近的最速下降路径与正 Re(p) 轴的夹角,设φ是f′′(pan)的相位角(φ∈(-π,π)),当积分路径是从左往右走时则χ=反之则
由(35)式可知,G*(kr)中只有Gn(kr) 可能是e 指数函数.Gn(kr)是贝塞尔函数在椭圆面上的积分,与活塞面与界面的夹角α有关,而与接收点的位置无关.当活塞面与界面平行时α=0,由(18)式得Gn(kr)=0 (n≥1) 和G0(kr)=又因所以α=0 时Gn(kr) 不是e 指数函数.因此我们推测当α=0时,Gn(kr) 也不是e 指数函数,而数值计算表明确实如此,但这里不再给出详细结果.综上可知Gn(kr)不是e 指数函数,所以G*(kr) 中不含e 指数函数.
