基于级联光参量放大器的碱金属原子跃迁线波段压缩光源分析*

韩亚帅 张啸 张昭 屈军 王军民

1) (安徽师范大学,物理与电子信息学院,芜湖 241000)

2) (安徽师范大学,光电材料科学与技术安徽省重点实验室,芜湖 241000)

3) (量子光学与光量子器件国家重点实验室(山西大学),山西大学光电研究所,太原 030006)

4) (教育部-山西省-省部共建极端光学协同创新中心(山西大学),太原 030006)

碱金属原子跃迁线波段压缩态光场是量子信息以及精密测量领域的重要量子资源.碱金属原子跃迁线波长短(760—860 nm),受限于非线性晶体的灰迹效应,光参量放大器制备的此波段压缩态光场的压缩度有限,目前典型值约3—5 dB.本文在光参量放大器的理论模型基础上,结合原子跃迁线波段压缩态光场实验制备面临的问题,研究光参量放大器输出光场量子噪声随其物理参数的变化规律,获得最优的物理参数.构建了级联光参量放大器的理论模型,以此为基础分别在分析频率2 MHz和100 kHz,研究了级联环路光学损耗以及相位噪声对级联系统输出量子噪声特性的影响.研究发现,对于兆赫兹波段的压缩,在低的光路损耗以及位相噪声前提下,级联2—3 个光参量放大器可实现压缩的显著提升;对于低频段压缩,级联系统对压缩的增强较小.在目前的实验参数条件下,进一步探究了级联系统输出压缩态光场的量子极限以及频谱特性.本研究可为原子跃迁线波段压缩态光场压缩度的提升提供参考和指导.

1 引言

压缩态光场是一种重要的非经典光场,其光场的某一个分量的量子噪声可低于标准量子极限.从应用的角度来讲,可采用压缩态光场实现超越经典极限的计量[1]和传感[2]等.在量子信息科学领域,压缩态光场是实现连续变量纠缠[3]以及连续变量量子密钥[4]分发重要的量子资源.对应于碱金属铯和铷原子跃迁线波长的压缩态光场,在量子通信[5]和精密测量[6,7]等领域有着特殊的应用潜力.在量子通信领域,量子信息需要利用量子存储和纠缠交换实现远距离中继传输,而原子介质是量子信息存储和处理的理想介质,因此制备与原子系统相匹配的压缩和纠缠态光场对于构建量子信息网络显得尤为重要.磁场测量是精密测量领域的重要课题,基于原子自旋效应的磁力计是目前最灵敏的磁力计之一,利用原子跃迁线波段压缩态光场替代相干的探测光,有望实现超越经典极限的磁场测量灵敏度.

基于二阶非线性效应的简并光参量振荡器(DOPO)和简并光参量放大器(DOPA)是产生压缩态光场的标准技术.1986 年,Wu 等[8]在国际上首次采用此技术实验产生了压缩态光场,当时的压缩度仅有—3 dB 左右.近些年来受益于非线性晶体工艺以及镀膜技术发展,基于此技术产生的压缩态光场压缩度得到显著提高,2016 年Schnabel 研究组[9]最大获得了—15 dB 的1064 nm 压缩态光场,这是目前压缩态光场压缩度的最好指标.国内彭堃墀研究组[10]2019 年实验实现压缩度约—13.8 dB的1064 nm 压缩态光场,这是国内压缩态光场的最高记录.与红外波段压缩得到显著提高形成鲜明对比的是,碱金属原子跃迁线波段压缩态光场压缩度提升缓慢.在860 nm 处,Furusawa 研究组[11,12]分别在2006 年和2007 年获得了—7 dB和—9 dB 的压缩.在共振于铯原子D2线的852 nm 处,张天才研究组[13]在2020 年获得了—4.3 dB 的压缩.对于波长更短的铷原子D1线795 nm 压缩态光场制备,国内外很多研究小组也开展了相关研究,Furusawa 研究组[14]和Lam 研究组[15]分别在2006 年和2007 年获得了—2.75 dB和—5.2 dB 压缩态光场.本文作者[16,17]也在795 nm 压缩态光场实验制备方面做了一些工作,在2016 年获得了—5.6 dB 的压缩态光场.

基于DOPO/DOPA 获得的795 nm 压缩态光场的压缩度相比1064 nm 波段结果要低很多,其原因在于795 nm 比1064 nm 波长短很多.波长越短,用于DOPO/DOPA 的非线性光学晶体以及镜片吸收损耗也越大.更重要的是,DOPO/DOPA需要795 nm 的倍频光397.5 nm 紫外光抽运,目前此波段最佳的非线性晶体是PPKTP,其对397.5 nm 紫外光存在强的吸收(20%左右)[18],此吸收会诱发晶体对红外光的吸收增强,即所谓的蓝紫光诱导的红外吸收[19].当紫光功率进一步升高,还会诱发灰迹效应[20,21],对非线性晶体造成损伤,进而制约DOPO/DOPA 输出压缩度及其稳定性.因此,对于795 nm 压缩态光场制备的DOPO/DOPA,其与红外波段不同,需在低抽运功率下运行.在低的抽运功率下,通过优化DOPO/DOPA 腔的物理参数,使其获得最大的压缩输出,是本论文探讨的第一个问题.受限于低抽运功率以及额外的损耗,单个DOPO/DOPA 输出的原子跃迁线波长压缩度非常有限,需考虑其他途径提升其压缩度.很直观的一种方案是,可考虑级联DOPO/DOPA 实现对压缩的提升.DOPO和DOPA 分别输出压缩真空态和正交压缩态光场,压缩真空态光场平均光子数非常弱,控制其与抽运光场的相对位相技术难度较大,故构建级联系统时压缩源一般运转于DOPA模式.Zhang 等[22]在2008 年首次在实验上演示了级联DOPA 对压缩态光场的量子特性增强,Wang等[23]在2013 年理论上讨论了级联DOPA 的量子噪声特性的极限.上述工作主要针对红外波段DOPA,本文在原子跃迁线波段的单个DOPA 系统参数优化的前提下,讨论级联DOPA 对原子跃迁线波段压缩的增强特性,同样也分析了级联系统的量子极限.与上述工作不一样的地方是,Wang 等[23]忽略了级联系统中光路的损耗以及位相延迟,本研究将这两个实验因素考虑进去,探讨其对级联DOPA系统量子噪声特性影响.此外,与前期研究主要集中在高频段的压缩不同,本论文分别在中高频段的2 MHz和低频段的100 kHz 这两个典型的分析频率处,对级联系统的压缩增强特性进行数值模拟和比较.最后,在目前的实验参数条件下,计算了利用级联DOPA 可达到的795 nm 压缩态光场的压缩度水平,进一步分析了其频谱特性,这可为高品质的原子跃迁线波段压缩态光场实验制备提供参考和依据.

2 理论分析

2.1 DOPA 基本理论

考虑抽运光单次穿过、下转换光腔内简并的光参量放大器(DOPA),如图1 所示.假设抽运光场的强度远大于信号光场,抽运光场可近似看作经典光场,此DOPA 内腔场的朗之万方程可写成[24]:

其中,τ为信号光在腔内往返一周的时间;T1为DOPA 为输出耦合透过率,L1为内腔损耗,γ=T1+L1代表腔总的损耗;κ为非线性耦合效率,其正比于抽运场振幅和晶体的二阶非线性系数;符号 ±分别代表DOPA 运转的两种状态,+代表参量放大状态,— 代表参量反放大状态.

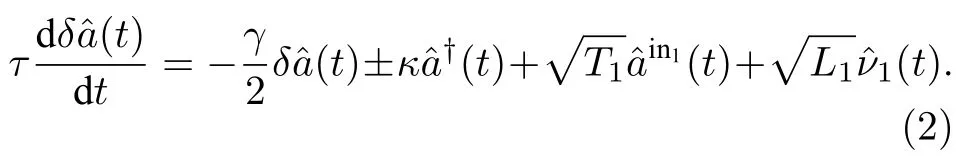
此处定义了参量m1,n1,m2,n2:

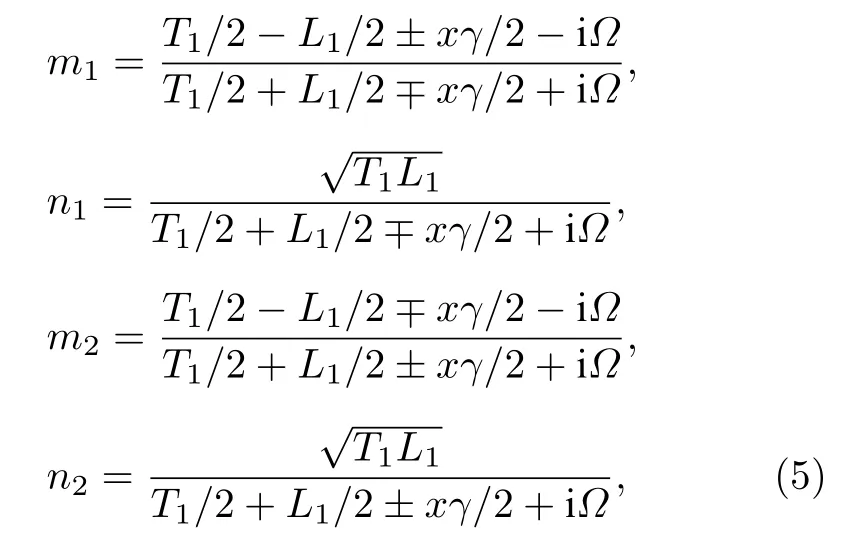
式中,Ω2πfτ,f即为测量中关注的分析频率;此处定义抽运参数x,其与非线性耦合效率κ和腔内总损耗γ有关,即x=2κ/γ.此处考虑DOPA处于参量反放大过程,上述公式中的±取—,∓取+,即产生正交振幅压缩态光场.由式(4),可求得DOPA 输出光场正交分量噪声方差:

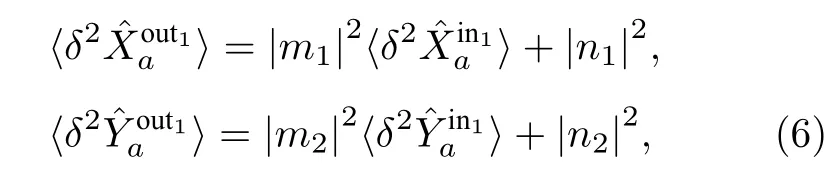
当入射光场为相干态或真空态光场时,式(6)可简化为

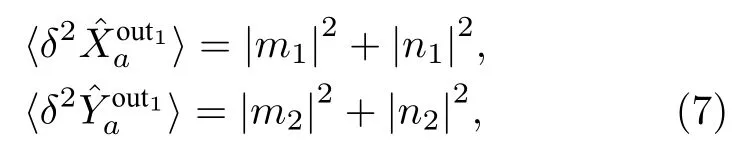
通过简单的数学变换,可得:

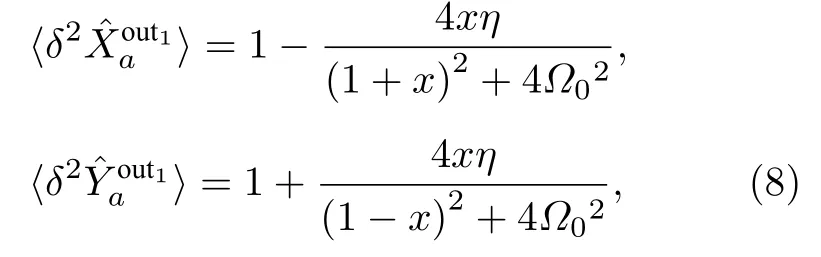
此处,定义腔的逃逸率η=T1/(T1+L1);定义腔的调谐参数Ω0=2πf/γ,其中γ=c(T1+L1)/l为腔的衰减率,l为DOPA 腔长;抽运参数x可写成抽运功率p的形式,即x=(p/pth)1/2,pth=(T1+L1)2/4Enl为DOPA 阈值,Enl为非线性晶体归一化的转换效率.

2.2 级联DOPA 的理论分析

相比红外波段,原子跃迁线波段压缩光制备的DOPA 系统抽运功率低,并且内腔损耗相对高,所以单个DOPA 产生的压缩度有限,考虑通过级联多个DOPA 实现压缩度的提升.级联DOPA 结构如图2 所示,假设系统中每个DOPA 的参数均相同,前一个DOPA 的输出光场作为下一个DOPA的输入光场,以此类推,需要注意的是每两个DOPA之间会不可避免的引入光场的损耗以及位相延迟,假设两DOPA 引入的损耗及位相延迟相等,分别记为L和φ.

图2 级联DOPA 结构示意图Fig.2.Schematic diagram of cascade DOPA.

DOPA1输出光场经过损耗L和位相延迟φ后,作为DOPA2输入光场,可关联写成如下形式:

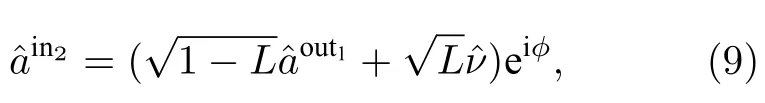
根据正交算符定义,进一步将算符线性化,可得到DOPA2输入光场和DOPA1的输出光场正交分量噪声方差之间关系:

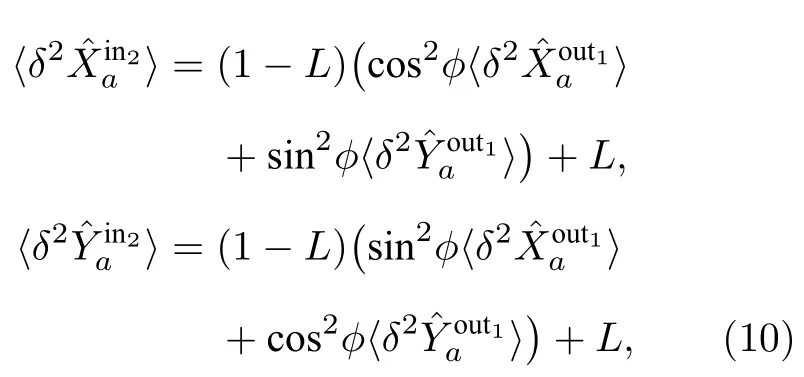
根据DOPA 输入输出关系(7),可得到DOPA2输出光场正交分量噪声方差:

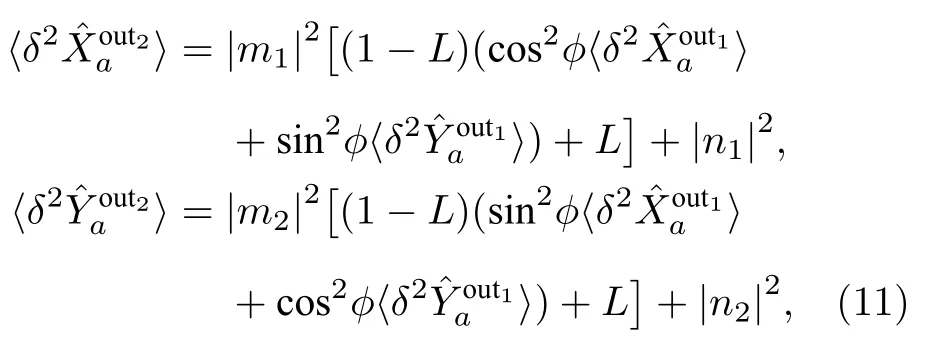
以此类推,可得到第n个DOPA 即DOPAn输出光场正交分量噪声方差:

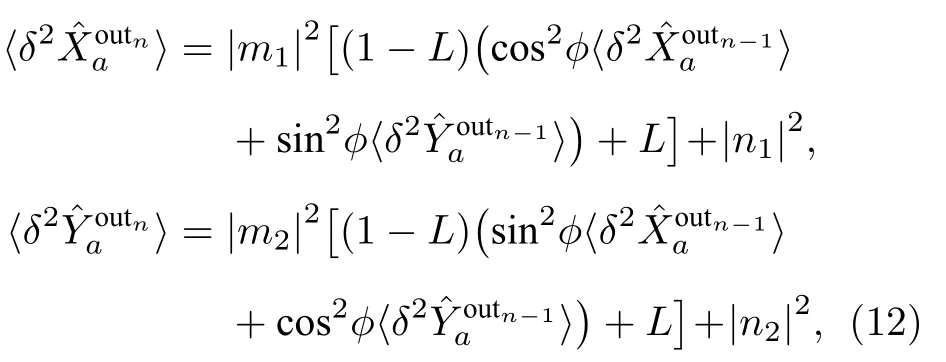
当第一个DOPA 参数确定时,通过式(8)可求得其输出光场噪声方差,进一步给定传输光路中的损耗L和位相延迟φ时,可根据式(12)通过数学迭代的方法分析DOPAn输出光场的噪声特性.

3 模拟结果及讨论

3.1 单个DOPA 系统的参数优化

首先,讨论铷原子D1线795 nm 压缩态光场制备的DOPA 系统设计和优化.795 nm 波段处于近红外接近可见光波段,DOPA 需要795 nm 倍频光397.5 nm 紫外光作为抽运光场,而此波段最佳的晶体PPKTP 对紫外波段吸收较强,为了避免非线性晶体的灰迹效应以及晶体损伤,对紫外抽运光的功率有限制.在确定的抽运功率下,通过优化DOPA 参数以获得最高的压缩态光场是本节讨论的核心.采用文献[16]中的DOPA 参数进行理论分析,DOPA 采用四镜环形腔设计,腔长600 mm,腔内放置15 mm 长PPKTP 晶体,晶体中心位置腰斑40 μm,根据腰斑可求得晶体非线性转换效率Enl=1.8%/W,内腔损耗L1=0.5%.在同样的腰斑下,Hétet 等[15]推荐将紫光功率限制在50 mW,从而避免灰迹效应,此处设置抽运功率p=40 mW.已知上述参量的前提下,选取合适的输出镜透过率T1对于可输出的压缩度至关重要.从式(8)可看出,DOPA 输出压缩度与抽运参数x和腔的逃逸率η均成正比,输出耦合镜透过率T1增大时逃逸率η增高,但是同时会导致DOPA 阈值升高,进而导致抽运参数x减小,二者存在制约,所以在确定的抽运功率下总存在一个最优的输出镜透过率,保证最佳的压缩输出.

采用上述DOPA 物理参数,根据式(8),数值模拟了DOPA 输出正交振幅光场压缩度随输出耦合镜透过率T1的变化,如图3 所示.数值模拟结果与理论预期一致,对于选取的两个分析频率处,均存在一个最佳的透过率Topt使DOPA 输出压缩度取极值.对于2 MHz和100 kHz 而言,最佳的透过率分别为7.7%和5.9%.由此可发现,在确定抽运功率前提下,DOPA 输出压缩度在各个分析频率处的极大值对应的最佳透过率是不同的.为了表征此特性,进一步数值模拟了DOPA 最佳的输出耦合镜透过率Topt与分析频率f的依赖关系,以及在Topt时可获得的压缩度,如图4 所示.图4 中的黑色实线代表了在各分析频率对应的Topt下,DOPA 输出的光场压缩度随f的依赖关系,分析频率越低,理论上DOPA 输出的光场压缩度也越高.插图给出了Topt随分析频率f的变化曲线.在分析频率从0 增至5 MHz,Topt从5.9%增至13.9%,这说明对于低频压缩和MHz 频段压缩的优化,DOPA最佳的Topt选取是有明显差异的.

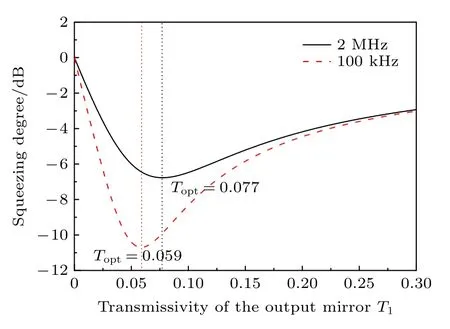
图3 DOPA 输出光场压缩度随输出耦合镜透过率的变化Fig.3.Squeezing degree of the output field versus the transmissivity of output coupler for the DOPA.

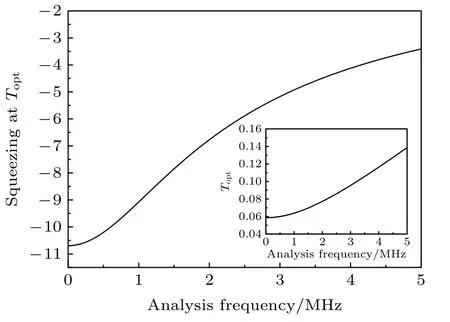
图4 在各个分析频率对应的最佳输出耦合镜透过率Topt 下,DOPA 输出的光场压缩度随分析频率f 的变化,插图给出了Topt 与分析频率f 的依赖关系Fig.4.Squeezing degree of the output filed versus analysis frequency for the DOPA at Topt of each frequency,inset shows dependence of Topt versus analysis frequency f.

上述讨论可得到一个重要的信息,对于DOPA系统的设计和优化,其与关注的测量频率或者分析频率是有关系的,当抽运功率和分析频率确定后,可根据上述方法寻求最佳的输出耦合镜透过率Topt,以在此抽运功率和分析频率处获得最优的光场压缩度.对于上述795 nm 压缩态光场制备的DOPA,在抽运功率p=40 mW和分析频率f=2 MHz 分析频率处可确定Topt=7.7%,可预期输出—6.77 dB的压缩,考虑10%的测量系统损耗,可测得的压缩为—5.39 dB.此结果与本作者2016 年发表的实验论文[16]中的结果相比,虽然输出压缩度无明显提升,但是获得此压缩的抽运功率显著降低,压缩度的稳定性有望显著提高.而对于795 nm 低频段的压缩,以100 kHz 为例,预期可获得—10.69 dB 压缩,同样考虑10%的测量损耗,可测量到—7.53 dB压缩,目前在实验中只观测到大约—2.80 dB[17],这主要受限于光源以及探测系统的低频噪声.

3.2 级联DOPA 系统压缩增强的理论分析

接下来讨论级联的DOPA 系统对795 nm 波段的光场压缩的提升效果.假设级联系统中每个DOPA 均相同,其参数同样与文献[16]中的参数相同,即:腔长l=600 mm,非线性转换效率Enl=1.8%/W,内腔损耗L1=0.5%,抽运功率p=40 mW.根据3.1 节分析可知,DOPA 在分析频率2 MHz和100 kHz,对应的最佳输出耦合镜透过率Topt分别为7.7%和5.9%.采用以上DOPA 参数,可确定参量m1,n1,m2和n2,当两DOPA 之间光场的损耗L和位相延迟φ确定时,可根据式(7)和式(12)分析级联DOPA 系统输出光场的噪声特性.首先,假设传输光路中的位相延迟φ为2π 的整数倍,数值模拟了级联DOPA 系统输出正交振幅压缩态光场的压缩度随损耗L的变化曲线,如图5 所示.图5(a)代表分析频率f=2 MHz 的结果,而图5(b)为f=100 kHz 的结果.从图5(a)可看出,传输环路损耗L比较低的时候,级联系统对压缩增强的效应较明显.当损耗L=0 时,级联两个DOPA可将单DOPA 输出光场的压缩度提高3 dB,级联3 个DOPA 可再提高0.7 dB,进一步级联DOPA,压缩增强效果不再明显,从图5(a)可看出n=3和n=4 的结果很接近.随着光路传输损耗L增大,级联DOPA 的压缩增强效应作用会随之减弱,当损耗增加到50%以后,压缩增强效果主要体现在第2 个DOPA,后续的DOPA 对压缩增强的效果基本可忽略.而对于分析频率f=100 kHz 的结果,如图5(b),级联系统对于此频段压缩增强效果非常微弱,与兆赫兹波段结果有较大差异.

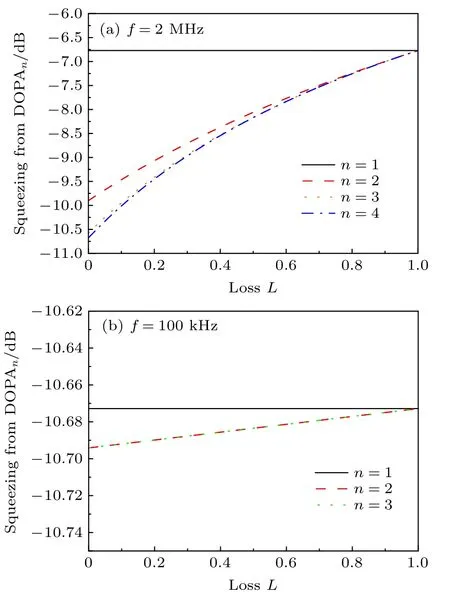
图5 级联DOPA 输出光场压缩度随传输光路损耗L 的变化 (a)分析频率f=2 MHz;(b)分析频率f=100 kHzFig.5.Squeezing degree of the output field versus the loss of optical loop for the cascaded DOPA:(a) f=2 MHz;(b) f=100 kHz.

此处,分析上述现象背后的物理.对于单个DOPA,其输出光场噪声如式(7),包括两部分贡献,前一项代表入射光场噪声贡献,当入射光为相干态时,其值为|m1|2,而后一项为DOPA 内腔损耗引入的真空场贡献,其值为|n1|2.对于分析频率f=2 MHz,代入DOPA 参数可求得|m1|2=0.137和|n1|2=0.074,说明入射光场噪声贡献占主要成分.先忽略传输光路损耗L,第1 个DOPA 输出的压缩态光场作为第2 个DOPA 输入光场,第2 个DOPA 以|m1|2的倍数缩小第1 个DOPA 输出光场噪声方差,同时会再耦合进新的真空场噪声方差|n1|2,如式(12)所示.DOPA 数目增加,按照此规律演化,当DOPA 数目增加到3 个以上时,式(12)中的第1 项入射光场噪声项经两次|m1|2倍数缩小后,其值会远小于第2 项腔内真空耦合项|n1|2,此时再增加DOPA 数目对压缩增加效果不会有太大贡献.而对于分析频率f=100 kHz,根据DOPA参数可求得|m1|2=0.0004和|n1|2=0.085,从此结果上可看出DOPA 内腔损耗引入的真空场噪声占据主要成分,每级联一个DOPA 均会引入新的真空场噪声,所以级联DOPA 系统无法实现对100 kHz频段的压缩增强.前面的讨论假设无传输光路损耗,而有光路损耗的情况时,相当于对每个DOPA输出光场噪声衰减后再进入下一个DOPA,其物理与上述讨论一致.

前文讨论了级联DOPA 系统输出压缩度与传输光路损耗L的依赖关系,接下来讨论传输光路的位相延迟φ对级联系统输出压缩度的影响.DOPA是相敏的光学参量放大器,前1 个DOPA 输出压缩态光场并不是简单注入第2 个DOPA 即可实现压缩增强,需严格控制其位相,此处位相指的是注入的信号光与抽运光的相对位相.为了简化计算,先忽略传输光路损耗L,根据式(12)数值模拟了级联DOPA 系统输出正交振幅压缩态光场的压缩度随传输光路位相延迟φ的变化曲线,如图6(a)和6(b)所示分别为分析频率2 MHz和100 kHz的结果.从图6 可看出随着级联的DOPA 数目增多,级联DOPA 系统输出光场的噪声对相位越来越敏感,这也意味着对于相位控制的要求也越来越高.将级联DOPA 与单个DOPA 输出结果交点的横坐标范围定义为RE,如图6(a)所示,相对位相锁定于此范围,级联DOPA 输出压缩会优于单个DOPA 结果,RE可以一定程度衡量位相锁定精度的要求.图6(b)和6(d)分别给出了分析频率2 MHz和100 kHz 的RE随级联的DOPA 数量n的变化曲线,此结果可为级联DOPA 系统实验设计提供一定参考.对于2 MHz 的结果可看出,级联2—3 个DOPA 可对此频段的压缩有比较显著的增强,其代价是需要提高相位锁定的精度;而在100 kHz处,级联DOPA 对压缩的增强很不显著,同时其对位相锁定要求相比2 MHz 要更高,因此从原理和技术上都很难通过级联DOPA 实现此低频段的压缩增强.

上述的讨论主要是在理想的条件下,接下来讨论在目前可达到的实验参数下级联DOPA 系统对于压缩的增强效果.对于传输光路中的损耗L,一方面来源于光路中光学元器件的散射、吸收以及剩余的透过率等,受益于目前镀膜技术以及镜片加工工艺的发展,此损耗已经可以降的很低.上述损耗是被动损耗,另一方面是主动损耗,注入DOPA 的信号光场需分出一部分做探测,将探测信号送入相位锁定环路,进而实现其与抽运光场的相对位相锁定.一般而言,分出的信号光越强,获得的误差信号越强,相位锁定也越稳定,但是同时对压缩的衰减也越强.综合以上两个因素,一般需要引入大概5%的光路损耗.而对于位相φ,可写成φφ0+Δφ,φ0和 Δφ分别是环路位相分布的均值和起伏.对于φ0,可通过相位锁定技术使其处于特定位相点,例如整数倍π,本文设置φ00;而 Δφ相当于将其从最佳的位相点偏移开 Δφ,等效于引入Δφ的位相偏置,从图6 可看出其大小对于级联DOPA输出的压缩影响也很大.目前,高压缩度压缩态制备实验均对系统的位相起伏进行了显著抑制,2018 年郑耀辉教授团队[25]已经将DOPA 系统中位相起伏限制到了4.42 mrad,本文也采用此位相噪声进行后续的计算.考虑5%的光路损耗以及4.42 mrad 的位相噪声,级联DOPA 输出光场在2 MHz 分析频率处的压缩随DOPA 数目的变化如图7 所示.图中分别给出了考虑和不考虑位相噪声两种情况的曲线,不考虑位相噪声时,级联DOPA输出光场的压缩度趋向于确定的极限值,这也和2013 年Wang 等[23]的结果一致.但是当考虑位相噪声时,尽管代入的位相噪声非常小,其依然对结果造成了比较大的影响,DOPA 数目超过4 以后,随着DOPA 数目增加,压缩反而退化.这是因为随着DOPA 级联的数目越多,其对位相也越敏感,位相噪声会将压缩和反压缩耦合,从而导致输出的压缩退化.当级联DOPA 数目小于4,级联压缩增强的效果大于位相噪声导致的压缩退化,压缩逐渐增强,当DOPA 数目超过4,位相噪声导致的压缩退化逐渐成为主要贡献,最终导致级联DOPA 输出的压缩逐渐退化.在实验可达到的光路损耗以及位相噪声下,级联两个DOPA 可将795 nm 压缩从—6.77 dB 提高到—9.67 dB,级联第3 个可将压缩提高至—10.25 dB.考虑大概10%的测量系统损耗,级联2 个和3 个DOPA 有望将测量的压缩从—5.39 dB提高到—7.05 dB和—7.33 dB.

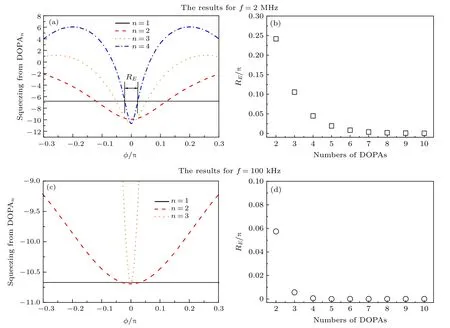
图6 (a)和(c)为级联DOPA 系统输出光场压缩度随传输光路位相延迟 φ 的变化;(b)和(d)为级联DOPA 可实现压缩增强的相位区间RE 随级联DOPA 个数的变化 (a)和(b)为分析频率f=2 MHz 的结果;(c)和(d)为分析频率f=100 kHz 结果Fig.6.(a) and (c) are the results for squeezing degree of the output field versus the phase delay φ of optical loop for the cascaded DOPA;(b) and (d) are the results for the phase region RE versus numbers of DOPA;(a) and (b) are the results for f=2 MHz;(b) and (d) are the results for f=100 kHz.

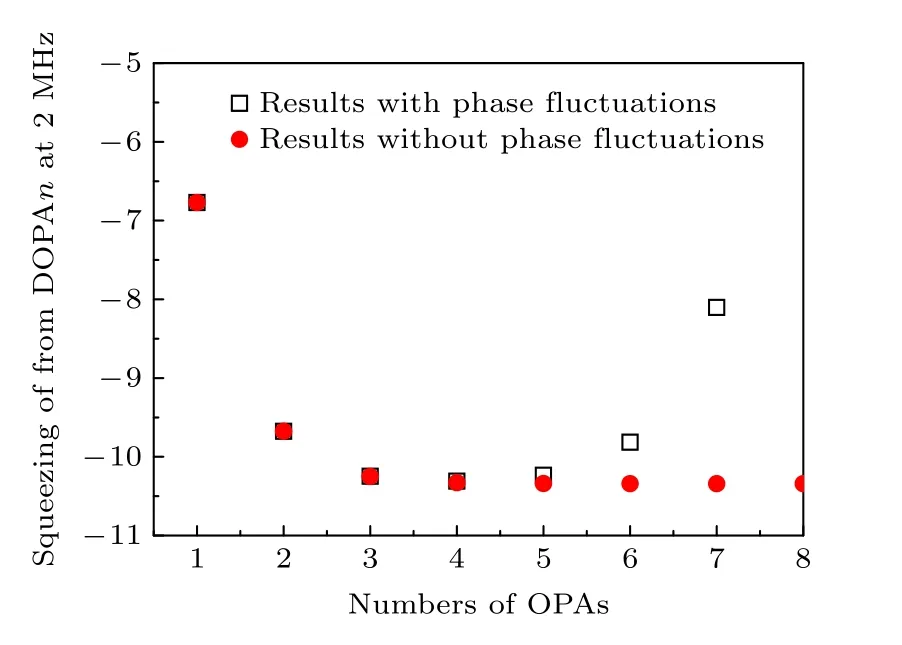
图7 考虑传输光路损耗以及位相噪声情况下,级联DOPA 系统输出光场在2 MHz 分析频率处的压缩度随DOPA 数目的变化Fig.7.The squeezing of the output field at 2 MHz from the cascaded DOPA versus the numbers of DOPA,at the circumstance of considering the loss and phase noise induced by optical loop.

上述讨论主要集中在2 MHz和100 kHz 这两个典型分析频率,最后将讨论扩展到一个宽的频率范围.根据式(7)和式(12),计算了级联DOPA 输出光场的噪声特性随频率的变化曲线,如图8 所示.DOPA 参数与上文一致,其输出耦合镜透过率Topt选择各分析频率最佳的透过率,并且考虑5%的光路损耗,图8(a)为未考虑位相噪声结果,图8(b)为考虑4.42 mrad 位相噪声的结果.从图8(a)结果可得出一个规律:单个DOPA 输出光场在低分析频率处压缩强,级联DOPA 对压缩增强的效应反而弱,而随着分析频率升高,单个DOPA 输出光场的压缩在减弱,但是级联系统对压缩增强的效应反而增强,此效应可在一定程度上扩展压缩的带宽.按照此规律演化,当n趋向于无穷大时,此系统将会输出理想的宽带压缩光.这和Wang 等[23]的理论分析结果一致,He 等[26]讨论级联非简并光参量放大器产生纠缠态光场时,也得到类似的结论.当考虑位相噪声时,其结果如图8(b)所示,n从1到3 的结果与图8(a)结果一致,当n进一步增大时,压缩的频谱相比图8(a)发生了较大变化,随着n增大压缩带宽反而变窄.这主要是随着DOPA增多,级联DOPA 系统对位相越来越敏感,并且从图(6)可看出,不同分析频率处对位相的敏感程度不同,低频段对于相位噪声显然更敏感,从而导致图8(b)中低频部分的压缩水平明显退化.从此结果可看出,通过级联多个DOPA 系统获得宽带的压缩光,实验上是存在技术瓶颈的.

图8 级联DOPA 输出光场的压缩特性随分析频率的变化 (a)忽略传输光路位相噪声结果;(b)考虑4.42 mrad位相噪声的结果Fig.8.Squeezing characteristics of the output light for the cascaded DOPA versus analysis frequency:(a) The result when the phase noise induced by optical loop is ignored;(b)the result when the phase noise of 4.42 mrad is considered.

4 结论

原子跃迁线波段压缩态光场制备的DOPA 需运转于低抽运功率下,本文基于光参量放大器的理论模型,对此低抽运功率DOPA 系统进行了理论分析和数值模拟.研究发现,在确定的抽运功率下,不同分析频率处均存在一个最佳的DOPA 输出耦合镜透过率,可在此频率处获得最高的压缩输出.数值模拟了此DOPA 最佳的输出耦合镜透过率和此透过率下输出的压缩度随分析频率的依赖关系,这对于原子跃迁线波段的DOPA 设计具有重要的指导意义.构建了级联DOPA 的理论模型,在模型中考虑了级联光路中的损耗以及位相噪声,在分析频率2 MHz和100 kHz 处,对级联系统的压缩增强效应进行了数值模拟.研究发现,级联两个DOPA 压缩增强效应最明显,随着级联DOPA 数目进一步增加,压缩增强效应迅速衰减.压缩增强效应还依赖于环路中的光学损耗和位相噪声,环路中的光学损耗和位相噪声越低,压缩增强效果越明显,因此通过级联系统实现压缩增强,需严格控制级联环路的光学损耗和位相噪声.此外,研究发现级联系统在低频和高频处的压缩增强效果存在较大差异,高频段级联DOPA 系统压缩增强效应显著,而在低频段级联DOPA 的压缩增强则很有限.本论文对上述差异背后的物理做了深入的分析和讨论,这有助于理解相敏的光学参量放大器.在考虑了级联光路中的损耗以及位相噪声前提下,探究了级联DOPA 系统的量子极限以及频谱特性.研究发现,由于位相噪声的限制,利用级联DOPA 产生理想的宽带压缩光仍是存在技术瓶颈的.本论文中的分析可为原子跃迁线波段压缩态实验设计提供有益的指导,为其在量子通信和精密测量领域中的应用奠定基础.