低能电子在玻璃管中的稳定传输*

李鹏飞 袁华 程紫东 钱立冰 刘中林 靳博 哈帅万城亮 崔莹 马越 杨治虎 路迪 Reinhold Schuch黎明 张红强7)† 陈熙萌‡

1) (兰州大学核科学与技术学院,兰州 730000)

2) (理化学研究所仁科加速器研究中心,和光 351-0198)

3) (中国科学院近代物理研究所,兰州 730000)

4) (哥德堡大学物理学系,哥德堡 SE-41296)

5) (斯德哥尔摩大学物理系,斯德哥尔摩 SE-10691)

6) (中国工程物理研究院电子工程研究所,绵阳 621900)

7) (兰州大学,稀有同位素前沿科学中心,兰州 730000)

分别对裸的直玻璃管和外壁与出入口两端面涂导电银胶的直玻璃管进行了低能电子穿透实验.穿透电子的倾角分布显示,穿透电子强度随倾角增大而减少,并且穿透倾角不会超过玻璃管的几何张角.还测量了玻璃管在倾角为—0.2°时的充电过程.对于裸玻璃管,在充电过程中,穿透率和角分布有显著的振荡现象.整体来看,穿透率随时间先下降后上升,最后在某个平均值附近振荡;角分布随穿透率变化同步变化,先向正角度移动再向负角度移动,最后在玻璃管的倾角附近振荡.对于涂导电胶的玻璃管,在充电过程中,穿透率和角分布稳定变化.穿透率随时间先下降后上升最后平稳,角分布随时间先向负角度移动再向正角度移动,最后在玻璃管倾角附近稳定.通过模拟电子与SiO2 材料的碰撞过程,提出了电子在裸玻璃管和涂导电胶玻璃管中的充电过程的物理图像.该物理图像能很好地解释电子在裸玻璃管和涂导电胶的玻璃管中充电过程的实验结果.最后,依据实验结果和物理图像给出了低能电子在玻璃毛细管中稳定输运的条件.

1 引言

由于低能电子对生物大分子有很大的损伤作用[1,2],电子束可以作为切割生物大分子链的工具.为了选择性地切割生物大分子的某一部分,要求电子束被聚焦到生物大分子的尺度(纳米量级).同时为了能在不损伤细胞活性的基础上进行切割,电子微束需要被从真空中引出做成外束,直接作用在切割位置.这些严苛的条件限制了电子束作为生物大分子切割工具的应用.直到一项用高能离子束对单个活细胞进行辐照的实验被报导[3].该实验将玻璃管做成出口为10 μm 的锥管,玻璃管尖端靠近细胞,离子由尖端出口对单个细胞进行定点辐照.实验实时观测了辐照剂量与细胞活性的关系.电子能否采用玻璃管进行定点传输成为能否对电子束应用该技术的关键.

离子的导向效应第一次被报导于2002 年.Stolterfoht 等[4]用Ne7+离子入射PET 微孔膜,初始入射离子的电荷沉积在微孔内壁表面,自组织形成电荷斑,电荷斑的库伦场阻止后续入射离子与微孔内壁碰撞,而使后续离子沿着微孔的轴向直接出射.因此绝大部分出射离子没有发生电荷态变化与能量损失.低能正离子在形成电荷斑的充电过程中,离子穿透率随充电时间上升然后达到平稳,同时离子的穿透角分布在微孔轴向角度附近振荡,最后平稳在微孔轴向角度[5,6].之后,大量的实验和理论研究围绕高电荷态离子在绝缘微孔膜[5-17]或单绝缘毛细管[3,18-22]中的穿越过程展开.目前正离子的导向效应机制已经被完全研究清楚[23,24].在导向效应过程中,除了入射离子自组织形成的电荷斑产生的库伦场决定了离子的穿越轨迹外,镜像电荷力起到了对离子束整形的作用[15,16].对于高能离子,离子不能完全被电荷斑的库伦场偏转而与管壁碰撞,散射过程必须被考虑[17].

但低能电子穿越绝缘微孔膜的实验结果与低能正离子有巨大的不同[25].在200—350 eV 能量的电子穿越高定向的Al2O3微孔膜的实验中发现[26,27],穿透电子包含弹性散射电子、非弹性散射电子和二次电子.非弹性散射电子和二次电子所占的比例是弹性散射电子的十倍以上.随着微孔膜倾角增大,弹性散射电子减少而非弹性散射电子和二次电子增大.弹性散射电子的角分布测量显示,弹性散射电子的出射角度与微孔膜的倾角相同,但角分布宽度远大于微孔的几何张角.充电过程的测量显示,弹性散射电子的强度随充电时间呈指数减少.弹性散射电子强度比正离子穿透强度小两个量级.针对该实验的模拟计算指出[27],电子与离子充电过程的不同来源于二次电子对入射电子形成电荷斑过程的影响,弹性散射电子不是来源于充电形成的电荷斑对电子的反射,而是来源于电子的近表面小角度散射,电荷斑的充电过程不再是必须的物理过程.然而在电子穿越PET 微孔膜的实验中,穿透电子中同样存在着大比例的非弹性散射电子,并且非弹性散射电子和弹性散射电子都沿着微孔的轴向出射[28].穿透电子的时间演化测量显示,穿透电子刚开始基本没有出现,一段时间后穿透电子强度快速上升到平稳态[29].非弹性散射电子的能损在上升阶段比平稳阶段大很多[30].对此结果,该工作的研究者认为,是由于电子特殊的沉积深度以及对应的电场强度变化导致的.然而这与理论模拟结果不同[31],模拟显示镜面散射和多次小角度散射是穿透电子经历的主要物理过程,而入射电子基本不会在微孔表面形成负电荷斑.由于二次电子激发,微孔内壁表面可能会形成正电荷斑,因而会吸引而不是排斥后续电子.这种电荷沉积模式会导致穿透电子强度随时间减小,这与Al2O3微孔膜的实验中的穿透电子强度随时间演化特征吻合.

以上研究中我们发现低能电子和低能离子穿越绝缘微孔膜的物理过程有很大不同.由于二次电子发射,沉积电荷的库仑场分布不像正离子那样支持电子穿越微孔膜,对出射电子的影响在两种不同材料的绝缘微孔膜中不同.

在电子穿越单玻璃管的研究中,情况变得更加复杂.在300—1000 eV 能量的电子穿越单根直玻璃管的研究中[32],穿透电子包含大比例的非弹性散射电子.穿透电子强度随倾角增加而下降,并且在倾角小于几何张角时下降更快.充电测量显示[33],除了0°以外的所有倾角,充电刚开始时几乎没有穿透电子,沉寂一段时间后,穿透电子强度随时间快速增强,之后穿透电子强度随时间振荡,不能达到平稳.当倾角大于几何张角时,穿透电子的能量随充电时间(即电荷的累积)而增加,直到与初束相同,同时其能量展宽变窄,直到与初束相同.当倾角小于几何张角时,穿透电子能量小于初束,能量展宽大于初束,并且两者基本保持常数,不随电荷的累积而变化[32].这些穿透电子的时间演化特性被作者解释为,沉积的负电荷斑逐渐靠近入口,并且突发性放电造成部分负电荷被中和[33].在500到1000 eV 电子穿越单玻璃锥管的实验中[34,35],这种穿透电子强度随时间演化特征同样被观察到,穿透电子强度在充电刚开始时沉寂之后随充电时间上升,但是穿透电子强度的上升速度比直玻璃管要慢得多.在锥管倾角为0°附近时,有三个穿透电子斑出现.这三个电子斑会随着倾角改变而移动,即中间电子斑的角分布中心在玻璃管的倾角角度上.对于不同入射能量的电子,穿透电子形成的出射斑的成分不同,500 eV 能量下,三个电子斑主要由弹性散射电子组成,而1000 eV 能量下,中间电子斑主要由弹性散射电子组成,其他两个电子斑主要由非弹性散射电子组成.穿透电子的弹性散射电子部分都会在倾角小于几何张角时消失.随着倾角继续增加到几何张角之外,只有在更大观察角上的穿透斑还存在,中心斑和另一侧的电子斑消失.这些复杂的出射电子角分布及其演化很难用一个物理图象解释清楚,可能源于电子在绝缘体孔内部复杂的输运物理过程.以上直管和锥管实验中,玻璃管均为裸管,管外壁没有涂导电层,这会造成各种不可预测且不稳定的电荷沉积模式,导致各种不一的实验现象.

我们之前开展了1.5 keV 的电子在400 pA/mm2的束流强度下对倾角为0°的直玻璃管和锥形玻璃管充电的实验[36].这些玻璃管均为裸玻璃管,外壁上没有导电层.这两种玻璃管的穿透电子都只有一个电子斑,并且穿透强度随时间有极大的振荡现象,同时电子穿透率比几何穿透率小四个量级.而对于外表面涂了导电层的锥管,在相同的能量下,用束流强度为21.3 fA/mm2的电子束做穿透[37].穿透电子随时间振荡的现象不再发生,穿透电子角分布同样是一个电子斑.穿透率随入射电荷的累积(充电时间)而衰减,直至平稳,同时穿透电子的角分布中心略微向0°移动.穿透电子在倾角为0°达到稳态后,其穿透率接近几何穿透率,其角分布宽度与玻璃锥管的几何张角相同.穿透电子的出射角度随倾角移动而移动,但穿透电子移动的角度小于倾角变化的角度.在几何张角内,穿透电子达到稳态后,其角分布宽度和穿透率基本不随倾角移动而改变,而在几何张角外,电子穿透率则快速下降.这些实验结果符合几何穿透,并且在充电过程中存在对穿透电子的阻塞效应.

从以上实验结果中不难发现,在电子穿越绝缘微孔的研究中,沉积电荷的作用仍然存有争议.同时,为了理解电子穿越微孔过程的物理图景,相应的计算工作也仍然不足.更需要指出的是,除了我们之前所做的电子穿越外壁涂导电层的玻璃锥管实验之外,其他绝大部分电子穿越单玻璃管的实验中,充电过程都伴有穿透电子的振荡现象.这种不可预测也不可控的振荡为利用玻璃管制作电子微束创造了极大困难.这要求我们探索稳定穿透电子所需要的条件,即玻璃管外壁的导电层是否起了作用,起了什么作用,还有没有其他条件可以让穿透电子保持稳定.在本文中,为了理解沉积电荷在电子穿越单玻璃管过程中的作用,同时为了探索稳定穿透电子所需的条件,测量了电子穿越裸的单玻璃管和外壁涂导电胶的单玻璃管的倾角分布和充电过程.之后通过CASINO 软件[38]模拟了电子碰撞SiO2材料的物理过程,依据计算结果创建了电子在SiO2材料上的充电图景.该图景很好地解释了我们所做的充电实验的结果.根据实验结果和物理图景,我们给出了稳定电子穿透所需要的条件.

2 实验装置

低能电子穿越高硼硅玻璃圆形毛细管的实验在兰州大学的低能粒子实验平台完成.实验平台的详细介绍可参考我们之前发表的工作[36,37].能量为0.9 或1.5 keV 的电子束从电子枪发出后经过偏转、聚焦、准直后进入金属制作的靶室.该靶室对外部磁场有屏蔽作用.靶架上的束斑大小为2 mm×2 mm.束流的发散角被控制在0.5°以内.0.9和1.5 keV 电子束的束流密度分别为—0.75 pA/mm2和—3.75 pA/mm2.靶室的真空度优于5×10—6Pa.穿越玻璃毛细管的电子被二维微通道板荧光屏探测器(详见文献[36,37])探测,可同时获取计数和角分布信息.

高硼硅玻璃毛细管被安装在一个五维调节装置上,可以沿着上下,左右,前后三个空间维度平移,可以在水平面(倾角,用α表示)和铅锤面(仰角)两个平面上旋转(详见文献[36,37]).在探测器平面上定义观测角度,将穿透电子在水平面和铅锤面上的移动分别称为φ角和θ角(如图1(a)所示).毛细管内径为0.5 mm,长为28.5 mm.为避免电子束打在玻璃管端面和外壁上,造成端面和外壁的充电,将一片铝箔紧靠在玻璃入口端,并在玻璃管入口中心处开一个略小于玻璃管直径的圆形孔.先完成1.5 keV 的电子穿透裸玻璃管的实验之后,再将玻璃管外壁和入口出口两个端面涂上导电银胶,进行0.9 keV 电子的穿透测量.

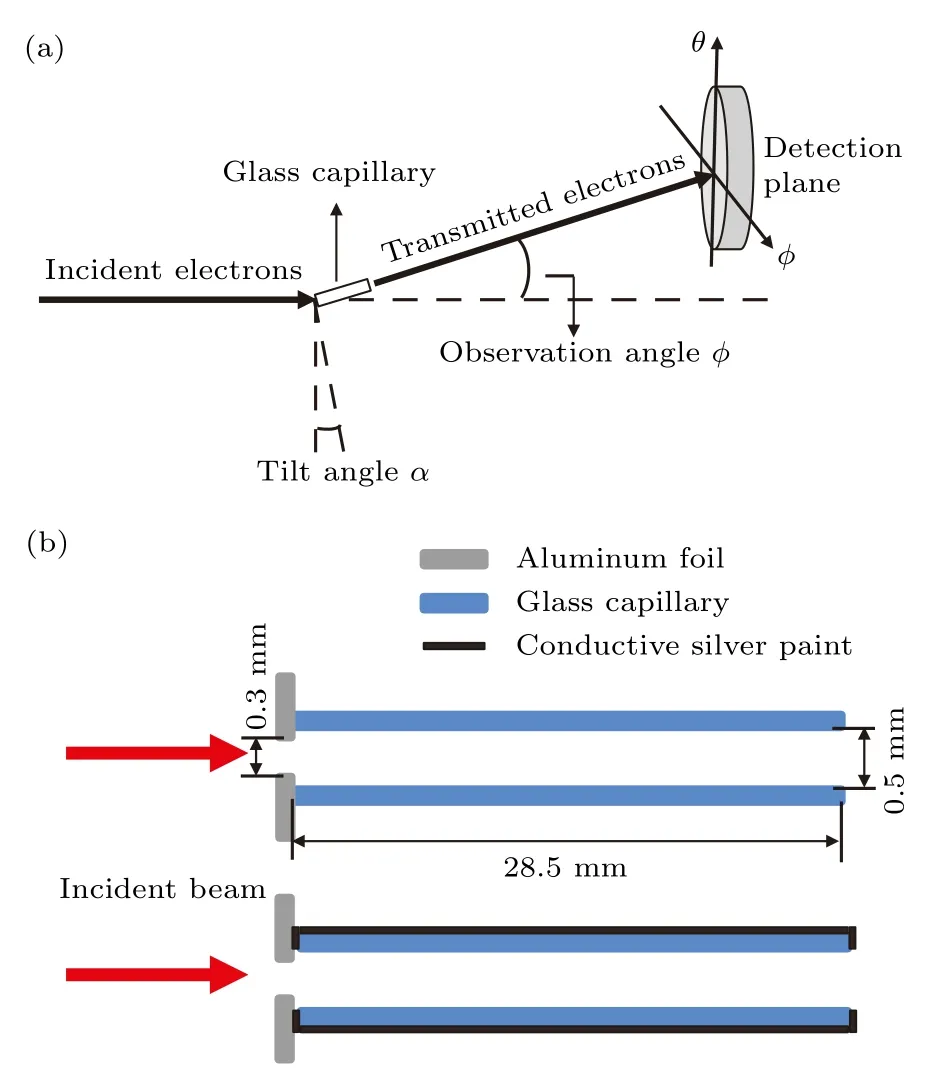
图1 (a)实验设备示意图;(b)裸玻璃管和涂导电胶玻璃管的示意图Fig.1.(a) Schematic drawing of the experimental setup.The tilt angle α between the axis of the glass capillary and the electron beam,the observation angles φ and θ relative to the direction of the electron beam are indicated;(b)schematic drawing of the glass capillary,bare (above),silver conductive paint brushed (below).

3 实验结果

图2 展示了在充电达到稳态时,1.5和0.9 keV电子的穿透率随玻璃毛细管倾角α的变化曲线.2 维MCP 探测器记录了所有的出射电子.这里定义几何穿透半高宽角度:

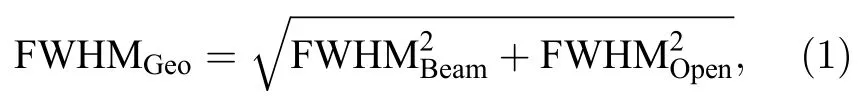
其中 FWHMBeam代表电子束的发散角度;FWHMOpen代表玻璃管的几何张角.计算出的几何穿透半高宽角度在图2 中用两虚线位置所示角度的角度差表示.对于1.5 keV 的穿透电子(图2(a)),其穿透率分布不呈高斯分布.穿透电子强度在倾角为0°时达到最大,且在倾角为0°(玻璃管中心)和玻璃管几何张角边界处有很尖锐的转折点.在大于几何穿透半高宽角度的倾角上,绝大部分1.5 keV的电子被阻止.而对于0.9 keV 的穿透电子(图2(b)),穿透电子强度随倾角的变化可以用高斯函数拟合,其半高宽为0.3°,远小于几何穿透的半高宽角度,同时也比1.5 keV 电子的倾角分布更窄.但毛细管倾角从0.3°增加到0.8°的过程中,电子穿透强度变化很微弱.

分别对1.5 keV 电子入射的裸玻璃毛细管和0.9 keV 电子入射的涂导电胶的玻璃毛细管在倾角为—0.2°时进行充电测量.每次测量前,都让玻璃管放电12 h 以上,防止上次测量之后玻璃管内残存着电荷,对测量结果造成影响.测量结果如图3 所示.

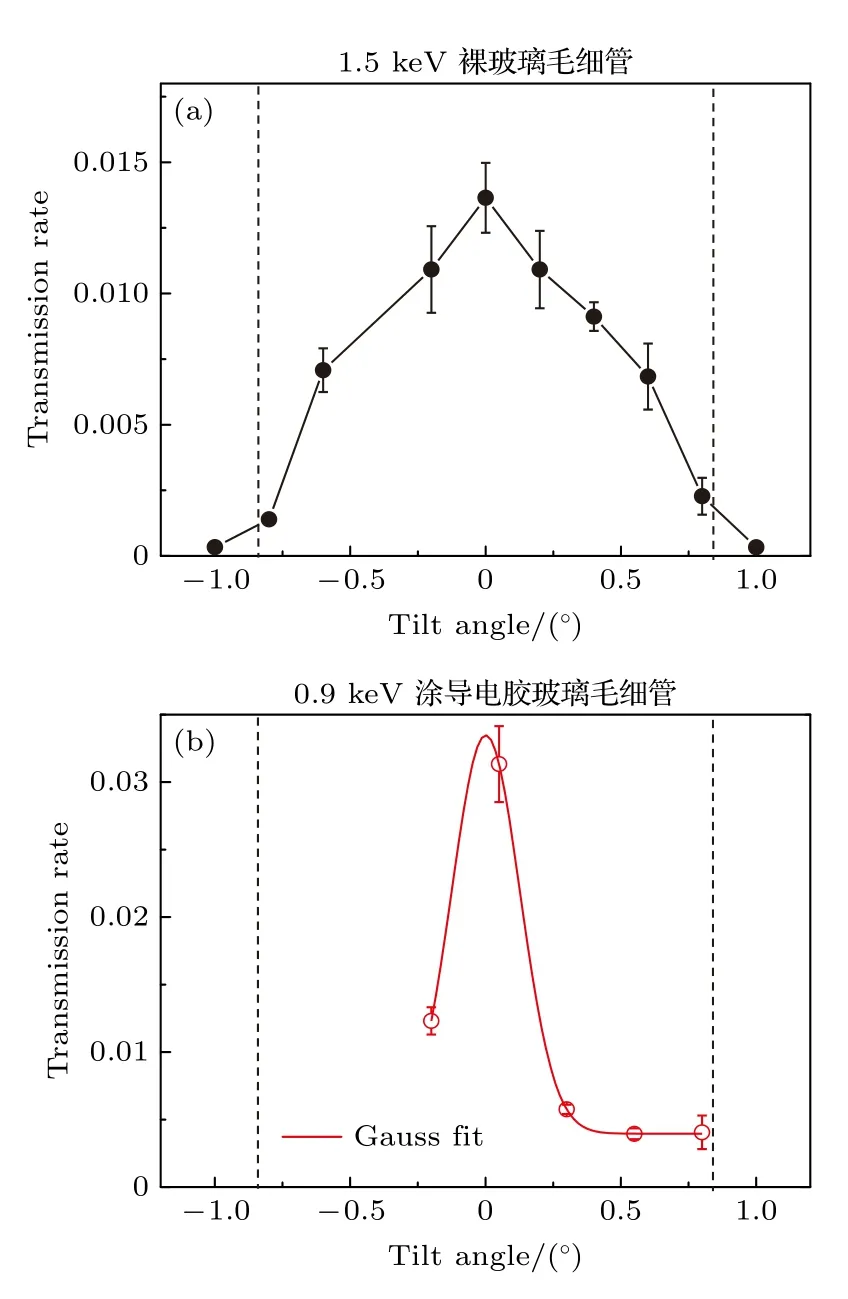
图21.5和0.9 keV 电子分别穿越裸玻璃毛细管(a)和涂导电胶玻璃毛细管(b)的穿透率随倾角变化的分布曲线.图中,虚线之间的角度代表几何穿透角.图(b)中,红线是高斯拟合线Fig.2.The steady-state values of the transmission rate as a function of the tilt angle for 1.5 keV electrons through bare glass capillary (a) and 0.9 keV electrons through conductive-coated glass capillary (b).The dash lines indicate the geometric transmission angle of 1.68° spread angle.The red solid line is a Gaussian fit curve of the measured 0.9 keV data.

图3(a)—(c)展示了1.5 keV 电子在倾角为—0.2°时穿透电子的穿透强度、穿透角分布随充电时间(充电电荷量)累积而呈现的极其复杂的变化过程.将图像在探测角φ 上投影,取投影最大值为图像中心值.第一阶段(0—340 s),穿透强度随充电时间累积而略微上升而后迅速下降至最小值,穿透电子角分布中心随穿透强度同步变化,从探测角0°向负角度方向略微移动,至—0.2°后由—0.2°迅速向正角度方向移动到0.5°.整体趋势上可以看作穿透强度随充电时间下降,穿透角分布随充电时间向正方向移动的过程.第二阶段(340—1000 s),电子穿透率随充电时间缓慢上升至0.02,穿透电子角分布中心随穿透率同步变化,由0.5°向负方向移到—0.5°.第三阶段(1000 s—end),电子穿透率随时间在0.015 附近上下振荡,振荡幅度为±0.005,穿透角分布中心跟随穿透强度同步振荡,振荡中心为—0.3°,振荡幅度为±0.3°,穿透强度下降时角分布中心向正角度方向移动,最多至0°,穿透强度上升与平稳时角分布中心向负角度方向移动至—0.6°.第三阶段的振荡周期约为600 s,其中3390 至4000 s 周期的角分布图像展示在图3 中.

图3 对倾角为—0.2°的裸玻璃毛细管(a),(b),(c)和涂导电胶的玻璃毛细管(d),(e),(f)的充电过程的测量.图(a)和图(d)分别为1.5和0.9 keV 电子的穿透率随时间演化曲线;图(b)和图(e)分别为1.5和0.9 keV 能量下的穿透电子在φ 平面的投影中心随时间的演化曲线;图(c)和图(f)为充电过程中选取的穿透电子的二维角分布图像;每个图像分别对应图(a)和图(c)中画红圈的位置Fig.3.Measurements of the charge-up process in the glass capillary at certain tilt angle (α=—0.2°).Investigations conducted with both electron energies of 1.5 and 0.9 keV.(a) and (d) show the measured time evolution of the transmission rates.(b) and (e) show the projection of the transmitted electron angular distribution on the φ-plane.(c) and (f) show the 2 D images of electron angular distribution at different stages during the charge-up process.Each image in Figure (c) and Figure (f) corresponds to a red circle as marked in Figure (a) and Figure (d),respectively.

从整体的趋势上看,1.5 keV 电子在裸玻璃毛细管中的充电过程可以看作为穿透强度随时间先下降后上升之后在0.015 的穿透率上振荡的过程,穿透角分布随穿透强度同步变化,先向正方向移动到正角度,再向负方向移动,然后在—0.3°的振荡中心上振荡.整个过程中,角分布向正方向最大移动到0.5°,向负方向最大移动到—0.9°,跨度达到1.4°,远大于毛细管的几何张角0.8°.

0.9keV 的电子在涂导电胶的玻璃毛细管中的充电过程的测量结果展示在图3(d)—3(f)中.穿透电子强度随时间先迅速下降至最小值(0—30 s,第一阶段)后缓慢上升(30—550 s,第二阶段)到穿透率为0.01 后保持长时间平稳(550 s—end,第三阶段).穿透角分布中心跟随穿透强度变化,略有延后,先向负角度方向移动,从0°到—0.9°(0—200 s),之后向正角度方向移动从—0.9°到—0.4°(200—900 s),最后穿透角分布中心极其缓慢地向正角度方向移动,由—0.4°到—0.3°(900 s—end).整个充电过程的角分布移动跨度为0.9°,只略微大于毛细管的几何张角0.8°,考虑到束流发散,可以认为与几何张角相同.对比0.9和1.5 keV 电子的充电过程,两者的穿透电子角分布中心跟随穿透强度有相反的移动方向,如穿透强度减少时,0.9 keV 的穿透电子向负方向移动而1.5 keV 的穿透电子向正方向移动.0.9 keV 电子的充电曲线平滑而稳定,不存在上下振荡.

4 物理图像和讨论

4.1 镜像电荷力

入射电子极化毛细管内表面产生镜像电荷,镜像电荷吸引电子靠近表面,改变入射电子的入射方向.圆柱内部,镜像电荷势被解析地表示为

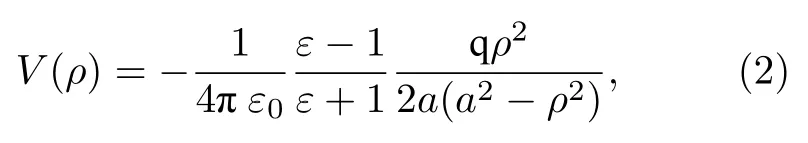
其中a是圆柱半径;ρ是电子距圆柱轴心的距离;ε0是真空介电常数;ε是相对介电常数;q是入射粒子电荷数.由于电子在离表面有一定距离的高度上就已经开始发生非弹性散射[39],我们在a– ρ≥0.1 nm 的范围内考虑镜像电荷势.计算出a– ρ=0.1 nm 处的镜像电荷势为13 eV.对于0.9和1.5 keV的电子,受镜像电荷势的影响,电子的入射角分别变为6.9+|α|度和5.3+|α|度,α为毛细管倾角.我们测量充电的角度α=—0.2°,故对于0.9和1.5 keV的电子,入射角分别变为7.1°和5.5°.

4.2 电荷沉积

入射电子与毛细管内壁碰撞,会发生与原子核相互作用的弹性散射、与核外电子相互作用的非弹性散射两种相互作用.只发生弹性散射的电子会通过镜像反射离开内壁,只与原子核发生动量交换,而不影响内壁的电性.发生非弹性散射的电子,会从以下两种形式沉积电荷:一是入射电子在非弹性散射过程中不断损失能量,最后沉积在毛细管体内,造成负电荷在体内积累;二是入射电子与靠近内壁表面的核外电子碰撞使核外电子从表面逃逸形成空穴,造成正电荷在靠近表面处累积.另外,除了入射电子造成的电荷累积,还需要考虑逃逸的二次电子的影响,为此需要知道二次电子的能量分布和角度分布.入射电子在材料体内发生非弹性散射也会产生空穴和二次电子,但二次电子射程极短,分布在形成的空穴附近,因此体内的空穴和二次电子分布总体形成的电荷分布可以看作电中性.

用CASINO 软件模拟了0.9 keV 电子在倾角为7.1°和1.5 keV 电子在倾角为5.5°下与SiO2材料的碰撞过程.空穴的深度分布如图4(a)和图4(c)所示,0.9和1.5 keV 电子造成了基本相同的空穴分布,绝大部分空穴分布在表面以下0.5 nm(两个原子层的厚度)内.0.9 keV 电子的空穴形成几率(即二次电子发射几率)为272%,1.5 keV 电子的空穴形成几率为254%.沉积的入射电子的深度分布如图4(b)和图4(d)所示,0.9 keV 能量下沉积的电子比1.5 keV 分布得更浅更密集.在0.9 keV能量下,沉积的电子的平均深度为7.7 nm,而在1.5 keV 能量下为16.7 nm.0.9 keV 的电子的沉积几率为 33%,而1.5 keV的电子为31%,两者基本相同.

图40.9 keV 电子在入射角为7.1°时造成的空穴深度分布(a)和电子沉积深度分布(b);1.5 keV 的电子在入射角为5.5°时造成的空穴深度分布(c)和电子沉积深度分布(d).X 方向为毛细管轴向方向,X 正向方向为入射电子具有最大动量的方向,(0,0)位置为碰撞点Fig.4.The holes distribution (a),(c) and deposited electrons distribution (b),(d) in depth for 0.9 keV electrons at tilt angle 7.1°(a),(b) and 1.5 keV electrons at tilt angle 5.5°(c),(d).The impact occurred at the (0,0) point.

两种入射能量下,二次电子具有相同的能量分布和角分布.其中 95%以上的二次电子能量在10 eV 以下.产生的二次电子以碰撞点为中心向四周均匀发射,与碰撞表面的夹角分布在 0°—90°之间,在40°左右的夹角下出射的二次电子最多.

计算结果显示,除了电子的沉积深度较浅外,0.9 与1.5 keV 的电子有基本相同的体内电子沉积几率,也产生了基本相同的空穴分布和二次电子分布.较浅的沉积深度造成较快的空穴电子复合速率,但同时也将导致更低的击穿电压.前者延长击穿时间,后者缩短击穿时间,两者效果相抵,并不会造成0.9 keV 电子的充电现象与1.5 keV 电子出现本质区别,尤其是造成两者穿透电子的角分布中心的移动过程完全相反.所以导电层的作用才是造成这种区别的主要原因.

4.3 物理图景

根据以上计算,给出电荷在玻璃毛细管内壁表面与体内沉积过程的物理图景:沉积的入射电子随时间在体内连续累积.二次电子发射造成的表面空穴也连续累积.由于沉积的电子深度较深,同时被空穴的电场屏蔽,玻璃管表面表现为正电场.未涂导电胶的情况下(图5(a)),在很短的时间内(在1 pA/mm2的束流强度下≪1s),正电场可以使二次电子做抛物线返回表面.刚开始时,正电场比较弱,二次电子在玻璃管轴向方向上射程较大,入口处发射的二次电子落到出口,而出口处发射的二次电子落到入口.两端的空穴电场被落回的二次电子屏蔽,并且空穴和电子快速复合,造成两端表面电场的强度的增长速度慢于其他部分.中间部分的正电场继续增强,二次电子射程越来越短.当出入口发射的二次电子可以落到中心时,中心部分的电场强度增速开始小于两端电场强度的增速.直至两端正电场强到使二次电子不能发出时,两端的正电场不再增强,同时其他部分因为得不到两端发射的二次电子的补充而造成表面电场相继增强,直至所有部分的表面电场达到出入口处正电场的强度.与此同时,体内沉积的入射电子持续累积,且没有上限.

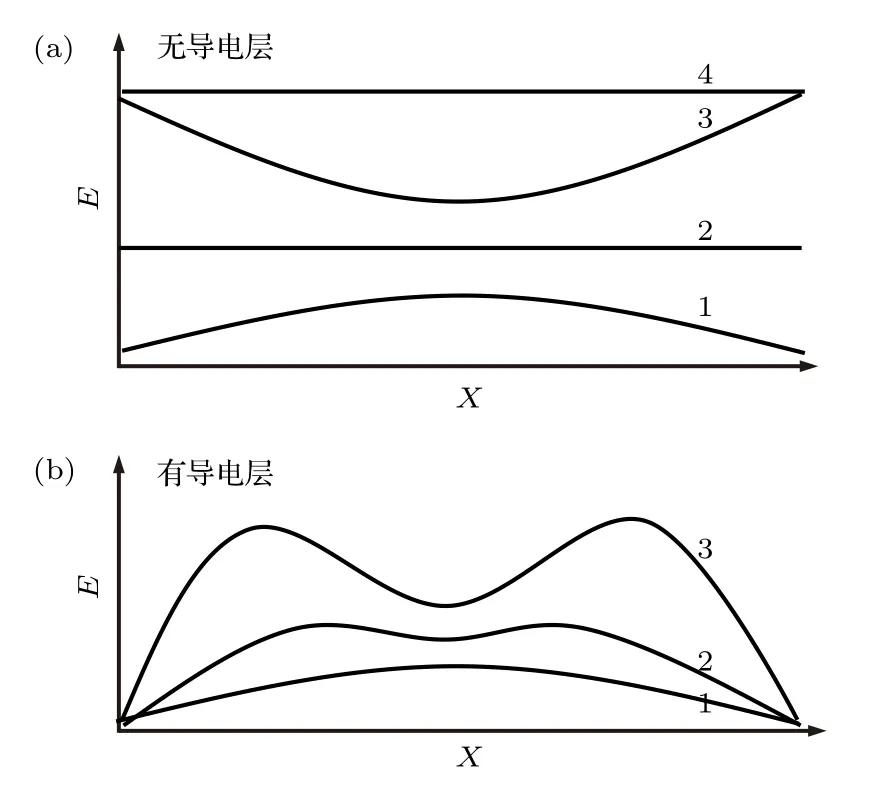
图5 无导电层(a)和有导电层(b)时,SiO2表面电场场强的演化示意图.图中的数字代表演化的先后顺序Fig.5.The evolution of the electronic field on the surface for the bare SiO2 (a) and conductive-coated SiO2 (b).The numbers in the figure stand for evolution sequences.

而对于涂了导电银胶的毛细管,入口与出口处由于导电胶接地而表现为零电势.故两端发射的二次电子永远具有一定射程,落到中间部分的表面上,屏蔽中间部分表面的正电场.表面电场最终呈现如图5(b)所示的双峰形.毛细管内壁表面只呈现很弱的正电场,对入射电子在毛细管内的飞行轨迹影响很微弱.

4.4 讨论

基于建立的物理图像,我们对裸玻璃管和涂导电胶玻璃管的充电数据做出解释.在倾角为—0.2°的情况下,入射电子与正角度一侧的玻璃管内壁碰撞.在第一阶段,对于裸玻璃管,电子与内壁碰撞造成二次电子发射,带正电荷的空穴在正角度一侧的玻璃管内壁表面累积,后续入射电子被吸引,向正角度方向移动,直至入射电子被吸引到正角度一侧的管壁上(图6(b)),造成穿透电子的下降;对于涂导电胶的玻璃管,由于导电层的存在,正电荷累积缓慢,表面正电场对入射电子的轨迹影响很小,因而入射电子只被沉积在体内的电子形成的负电场排斥,造成穿透电子持续向负角度方向移动,打在负角度一侧的玻璃管内壁上(图6(e)),使穿透电子强度减小.第二阶段,对于裸玻璃管,绝大部分电子被吸引至正角度一侧的管壁上,不能逃逸,造成电子在正角度一侧管壁体内迅速沉积,当体内电子达到一定密度后,后续的入射电子被体内电子形成的负电场排斥出内壁表面,穿透电子强度开始增加,并且穿透电子向负角度方向移动(图6(c)),与此同时,正角度一侧的管壁表面正电场仍会持续增强;对于涂导电胶的玻璃管,负角度一侧的玻璃管内壁被充电,电子被再次反射,向正角度方向移动(图6(f)),出射电子变多,穿透电子强度增加.第三阶段,对于裸玻璃管,1.5 keV 电子的平均沉积深度只有16.7 nm,当表面正电荷和体内电子密度累积到一定量时,16.7 nm 厚的绝缘层被高压击穿,表面空穴与体内电子迅速复合一部分,之后继续累积并再次击穿,如此反复,造成穿透电子计数的振荡和穿透电子角分布的振荡;对于涂导电胶的玻璃管,玻璃管内壁两侧的充电完成,电子经过两次由沉积电荷导致的偏转后基本从玻璃管轴向方向穿透.由于玻璃管内壁表面正电荷的积累被导电层大大限制,表面空穴与体内电子的电压差很难达到击穿电压,这个前提下,0.9 keV 电子的平均沉积深度只有7.7 nm,体内电子和表面空穴有较快的复合速率,能再次延长达到击穿电压所需要的时间,穿透电子强度和角分布长时间保持平稳.

图6 充电过程中,裸玻璃管((a)—(c))的和涂导电胶的玻璃管((d)—(f))的穿透电子在玻璃管内的轨迹示意图.红色箭头线为电子轨迹Fig.6.The diagrams for the trajectories of the transmitted electrons through the bare glass capillary ((a)—(c)) and the conductive-coated glass capillary ((d)—(f)) in the charging up process.

根据实验测量和理论分析,不难得到电子稳定穿越玻璃管的实验条件:1)管外壁和出入口两端要有导电涂层.导电涂层的存在极大地降低了毛细管内壁表面的正电场强度,降低了表面正电场和体内负电场之间的电压差.2) 允许的情况下选较低的电子入射能量.低入射能量的电子在体内的沉积深度较浅,在表面正电荷强度被导电涂层限制的前提下,能增加表面空穴和体内电子的复合速率.3)合适的电子束密度.电子束的流强过强时,体内电子和表面空穴复合率远远小于沉积速度,即使存在导电层也会发生放电.

5 结论

我们测量了1.5 keV 的电子穿越裸玻璃管和0.9 keV 的电子穿越外壁和出入口两端面涂导电银胶的玻璃管的倾角分布.发现穿透电子强度随倾角增大而减少,电子的倾角分布半高宽小于玻璃管的几何张角.对比测量了裸玻璃管和涂导电胶的玻璃管在倾角为—0.2°时的充电过程.发现裸玻璃管的电子穿透率和角分布随时间显著振荡,而涂导电胶的玻璃管的电子穿透率和角分布随时间是一个稳定变化的曲线.依据电子与SiO2材料的碰撞模拟结果,提出了电子在裸玻璃管和涂导电胶玻璃管中的充电过程的物理图像.该物理图像指出,玻璃管外壁和出入口两端面的导电层能极大地降低玻璃管内壁表面的正电场强度,很好地解释了电子在裸玻璃管中和在涂导电胶的玻璃管中的充电过程的实验结果.最后我们提出了电子稳定穿透玻璃管的三个实验条件,为以后利用玻璃锥管产生稳定的电子微束和外束的实验提供了方向.