基于精英策略的蚁群算法在AGV路径优化中的应用*

□ 孙宇翔，陈浩鹏，任传荣

(江苏科技大学 张家港校区，江苏 张家港 215600)

1 引言

在现代物流的仓储中，货物搬运效率的显著提升得益于自动引导车(Automated Guided Vehicle，AGV)的出现，也为企业节省了大量的劳动力成本[1]。在这种全自动化设备的运行过程中，为了搜寻一条相对更优的路径，使AGV在运行过程中可以避开所有障碍物的同时行驶较短的距离，依靠的是背后强大的算法。

传统蚁群算法的随机选择虽然能搜索更大的任务范围，有助于搜寻潜在的全局最优解，但是需要相对比较长的时间才能发挥正反馈的作用，致使算法在开始阶段收敛速度较慢。同时，蚁群算法具有正反馈的特性，若蚁群算法在开始搜索时受次优解影响，那么正反馈会使次优解很快占据优势，使算法陷入局部最优。针对上述问题，很多先前的研究者在蚁群算法的基础上做出了改进，曹新亮等[2]针对蚁群算法在初期搜索目标的盲目性，建立了新的数学模型，对开始的信息素浓度提前进行差异化设置，进而提高算法收敛速度；占伟等[3]在初始阶段就赋予了蚁群算法一个确定的搜索方向，在信息素更新策略上平衡全局和局部搜索的能力，尽力以最快的速度找到最优解；韩颜等[4]将粒子群算法和蚁群算法融合改进，在蚁群算法中设定栅格标识，从而增强小车的避障能力。

本文针对传统蚁群算法中存在的问题，加入了精英策略，通过模拟仿真来验证改进后的算法在搜索AGV运行的最优路径上的有效性。

2 蚁群算法逻辑

2.1 传统蚁群算法

通常认为，在蚁群算法开始之前，各目标点及路径上各点的信息素浓度一致为0，有τ0=τij(0)；用ηij(t)来表示启发函数，即在时刻t时，蚂蚁从目标点i转向目标点j的期望程度。

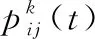
allowedk={C-tabuk}是t时刻蚂蚁下一步允许选择的栅格块(没有访问过的栅格)；tabuk(k=1,2,…,m)是禁忌表，记录已走过的栅格块。

2.2 改进蚁群算法的信息素更新规则

2.2.1 信息素更新策略

信息素的更新机制直接影响了蚁群算法整体的性能。在蚁群算法中引入遗传算法的精英策略[6]，使得蚂蚁在寻路的过程中，将每次迭代完成后的精英蚂蚁对应的解取出来，对精英蚂蚁的路径进行局部的信息素调整，即对每条精英路径依据长度赋予不同的比例参数ω，路径长度越小，则参数越大，信息量浓度也越大。这样，不仅增强了蚁群算法的正反馈机制，提升了算法效率，同时，采取局部信息素更新和全局信息素更新相结合的方式，避免了算法早熟收敛。

2.2.2 信息素更新规则

信息浓度更新规则如下所示：

最优路径的信息素更新规则：

其余蚂蚁相关路径中的信息素更新规则:

其中，w-r表示第r只精英蚂蚁的信息素更新比例参数，Δτbest(i,j)表示在当代循e只(即最短路径)精英蚂蚁在栅格(i,j)上释放的信息素浓度。

3 模拟仿真

3.1 栅格法建立环境

将蚁群算法应用于AGV小车路径规划之前，需要将实际环境虚拟化，即建立环境模型。在全局的路径规划中，使用频率最高的就算栅格法[7]。栅格法的建立过程就是在AGV的可运动范围内建立二维的平面直角坐标系，随后根据障碍物的布局、大小模拟出栅格区域的大小。把栅格分为障碍类栅格和可行驶栅格，对前者赋值为1，对后者赋值为0，这样机器人就可以根据栅格的属性值区分障碍物和可行驶区域。

3.2 仿真应用

该仿真模拟中采用20*20的栅格图作为仿真模拟环境，黑色代表障碍物，白色代表可移动区域。其中算法的具体相关参数如表1所示。

在Matlab中，分别使用传统蚁群算法和基于精英策略后的蚁群算法进行模拟，得到的结果如图1-4所示。

表1 改进后的蚁群算法相关参数

图1 传统蚁群算法路径图

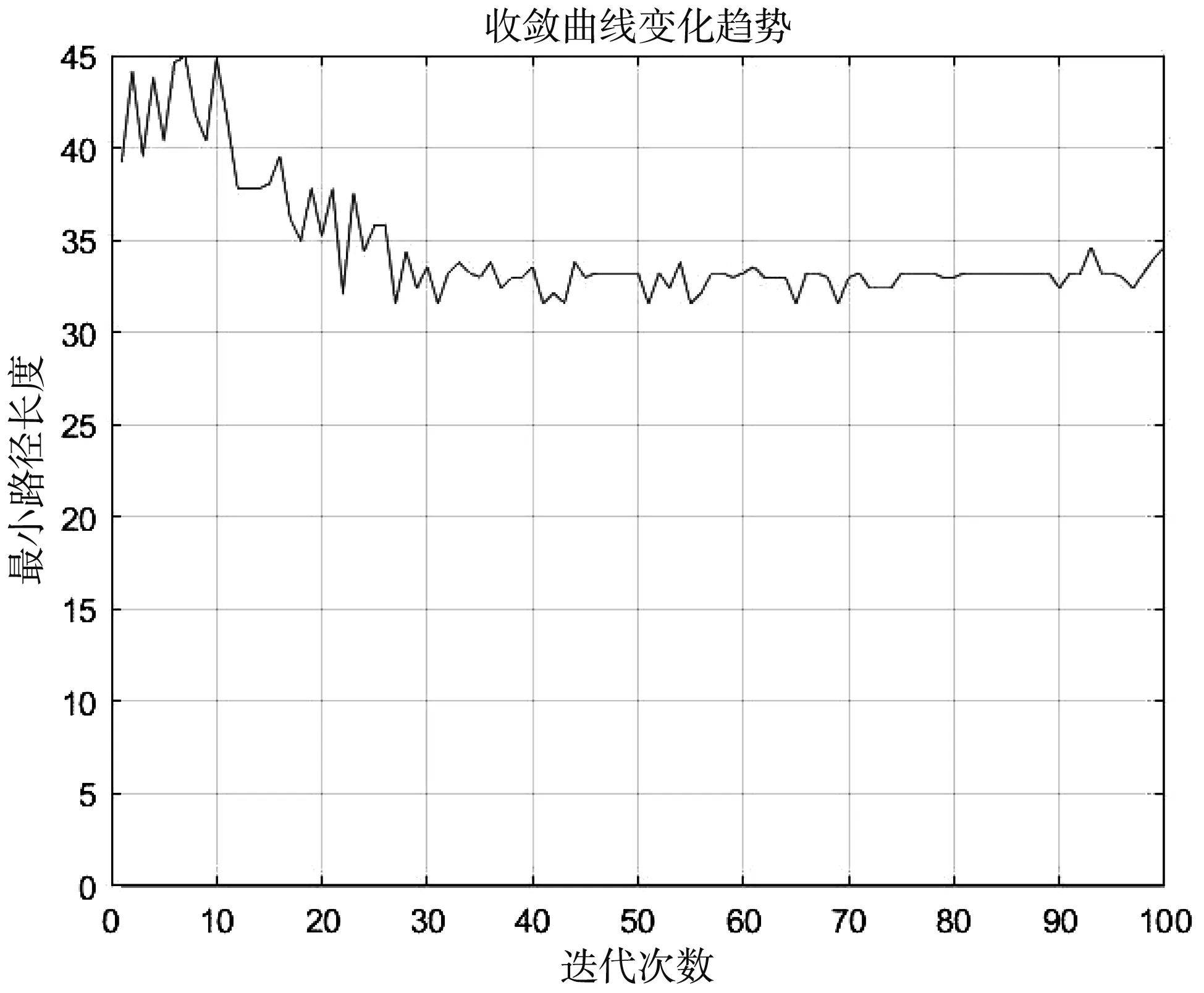
图3 传统蚁群算法收敛曲线

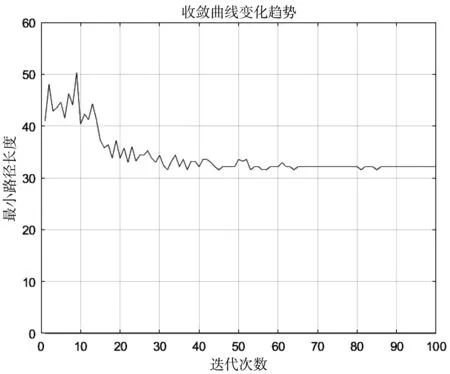
图4 精英策略下的蚁群算法收敛曲线

如图1和图2所示，用传统蚁群算法和改进后的蚁群算法运行得到的路径并不相同，经过数据比对，改进后的蚁群算法所生成的路径更优。

观察传统蚁群算法收敛曲线(见图3、图4)，可发现未优化的蚁群算法收敛不平稳、速度慢，最终所得到的路径较长。而改进后的蚁群算法所规划的路径更为集中，且集中在了最优路径的周围。

表2 改进前后路径长度及到达终点蚂蚁数量

通过比对生成的详细数据可以看到，传统蚁群算法搜索到的最优路径长度为33.20，而精英策略下的蚁群算法搜索到的最优路径长度为31.79，并且在两个算法运行的过程中，传统蚁群算法搜索到的可行解的平均值高于改进后的蚁群算法。

在两个算法各迭代100次的过程中，传统蚁群算法只有2279只蚂蚁最终到达了终点，而精英策略下的蚁群算法有4061只蚂蚁成功到达了终点，说明改进后的蚁群算法提高了蚂蚁的搜索效率。

在修改栅格法中障碍物的布局和更换目标点位置后，分别用传统蚁群算法和改进后的蚁群算法搜索路径结果，得出了8组优化前后的路径长度，并求出了优化比例。其结果如表3所示。

分析比对结果可知，总体来看，加入精英策略后的蚁群算法搜索到的最优路径长度相较于传统蚁群算法有所减少，在大多数情况下优化效果明显。

通过Matlab仿真后生成的相关数据可以看出，本文所改进的蚁群算法能够在复杂的环境下更快速地搜索到最优解，并且所得结果优于传统蚁群算法，也提升了算法运行过程中的搜索效率。

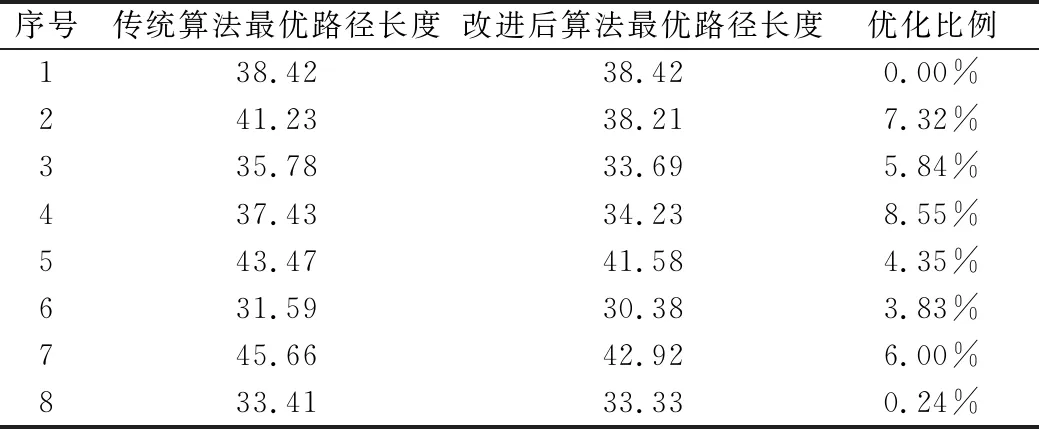
表3 优化前后路径长度及优化比例

4 结语

本文针对传统蚁群算法初期收敛速度慢、容易陷入局部最优解等问题，在传统蚁群算法的基础上加入了精英策略，运用对精英蚂蚁的信息素进行局部更新的思想，替换了信息素的更新规则。经过仿真模拟后发现，改进后的蚁群算法提高了算法的收敛速度和搜索效率，其搜索的路径结果更优，证实了该算法的可行性和有效性。