黄土丘陵沟壑区自然条件下不同辐射面蒸发蒸腾量的预测

贾 芳，樊贵盛

（1.山西农业大学水土保持科学研究所（山西省水土保持科学研究所），太原 030024；2.太原理工大学水利科学与工程学院，太原 030024）

0 引 言

蒸发蒸腾量（Evapotranspiration，ET），其物理意义是指水分从地球表面移向大气的过程，包括土壤与植株表面液态水或固相水的蒸发和植物的蒸腾[1]。它是研究区域水资源平衡的关键因素，也是管理和优化水资源配置的基础。在北方干旱半干旱地区，随着人类活动的加剧和扰动，使得区域ET值逐渐增大，产生了诸如径流衰减、地下水亏缺等现象，导致水资源紧缺危机日益凸显，因此，对自然条件下的ET值进行预测具有十分重要的意义。目前，ET值的获取主要包括直接法和间接法。直接测定法包括涡度相关法[2]、风调试法[3]、遥感法[4]、蒸渗仪法[5]等。间接估算法[6,7]主要包括经验公式法、水量平衡法、能量平衡与空气动力学联合法。其中，水量平衡法是计算ET值最基本的方法，也是目前一直使用的较为传统、应用最为广泛的方法[8]。王欣语、高兵等[9]利用水量平衡方程估算了青海湖水量的平衡变化及其对青海湖水位的影响；杨丽虎、徐迎春等[10]利用水量平衡法定量评估了引黄灌区土壤水与地下水的补给量；王青松、冯浩等[11]采用蒸散仪、水量平衡法探究了不同颜色地膜覆盖对春玉米农田蒸散量及蒸散结构的影响；刘中一、霍再林等[12]应用水量平衡法对河套灌区实施节水后作物生育期内区域耗水、地下水贡献及水均衡变化进行了定量研究。综上所述，目前对于黄土丘陵沟壑区自然条件下蒸发蒸腾量的研究较少。本文通过在黄土丘陵沟壑区布设15 个试验点，系统的研究了不同辐射面ET值的变化规律，以及坡向、坡度对ET的影响，在水量平衡法的基础上构建了月度ET值预测模型，并对其预测结果进行了验证。研究结果对黄土丘陵沟壑区农业生产、灌溉制度的制定、缓解水资源短缺现状、实现基于ET的水资源管理模式具有重要意义。

1 理论与方法

1.1 研究区概况

本文研究区主要布设在王家沟。王家沟位于吕梁市离石区王家沟村，是黄河一级支流三川河的一级支沟，由东向西汇入三川河支流北川河。王家沟流域面积9.1 km2，主沟道长4.6 km，平均纵坡7.6%，两侧有31 条支沟，均与主沟成直角相汇，还发育了众多的冲沟、切沟。流域内地形起伏变化大，地面平均坡度30°，沟坡比1.724，沟壑密度7.01 km/km2，沟道下切深度一般为60～80 m，具有典型的黄土丘陵沟壑代表性。布设试验点时考虑坡向、坡度、植物等因素，选择阳坡（西南坡、西坡、南坡）和阴坡（北坡和西北坡）为主要坡向布设观测点，在不同坡向上按照坡度不同布置观测点，一共布置15 个点，其中阳坡4 个测试点，阴坡11 个测试点。试验测试周期为2018-2019年，测试频次为每月一次，测试期为每年3-10月，每月21日进行土壤含水量取样测定，每年测定8次。试验点基本情况如表1所示。

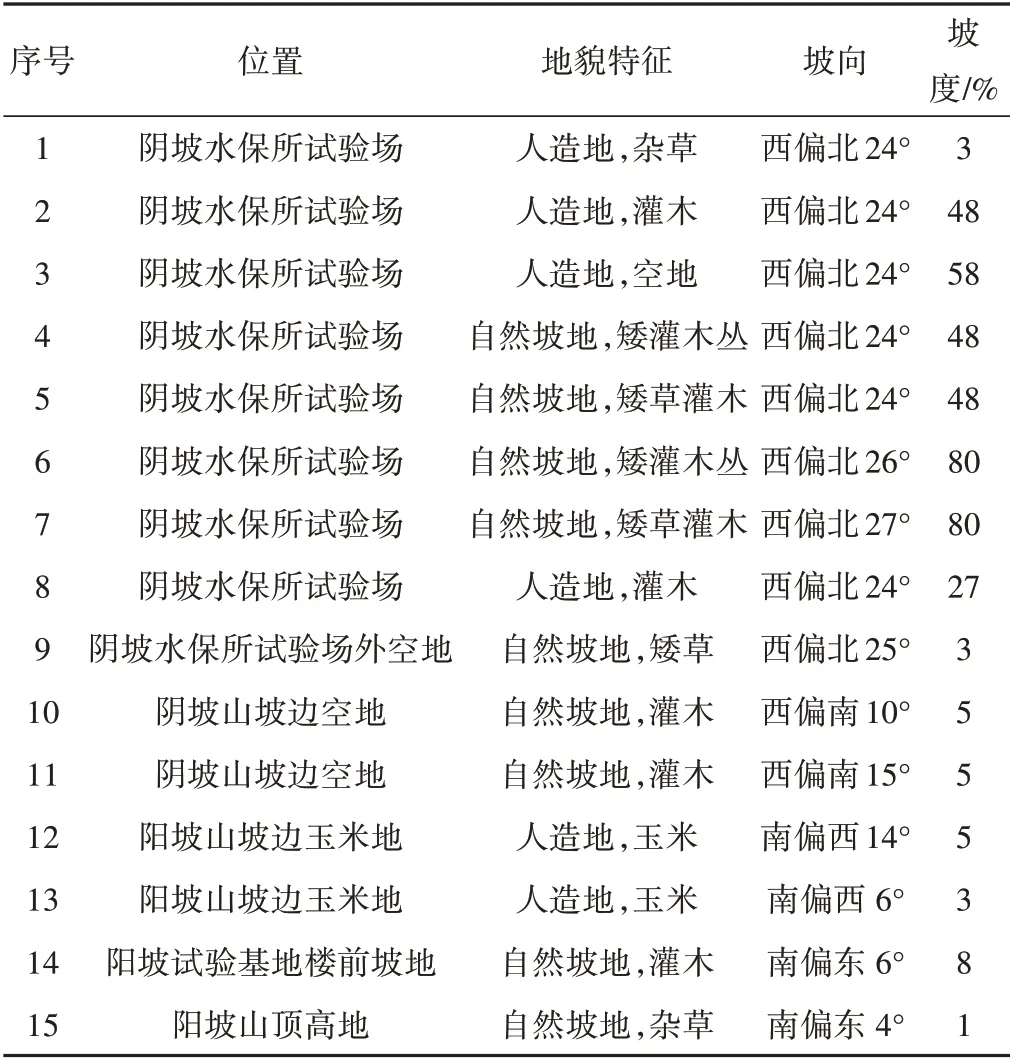
表1 试验点基本情况Tab.1 The basic situation of the test site

1.2 ET计算公式

水量平衡法源于Grier 等提出的水文平衡理论，即水分在土壤、植物叶面和气候之间运移时，存在着水分的动态平衡关系。水量平衡法主要用于揭示研究区域在研究时段内的水循环过程、分析水分循环要素间的定量关系[13]。

计算ET水量平衡方程为：

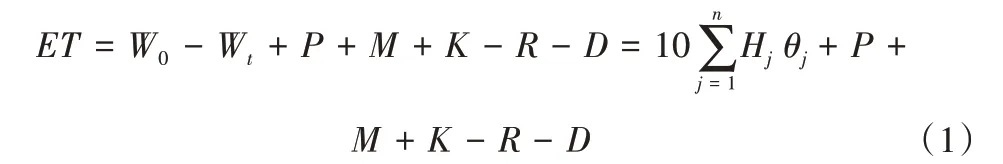
式中：ET为计算时段内的蒸发蒸腾量，mm/月；W0、Wt为计算时段始、末土壤储存水量，mm；P为计算时段内的降水量（不考虑植物截留），mm；M为计算时段内的灌溉水量，mm；K为计算时段内的地下水补给量，由于研究区域地下水埋深大于5 m，文中该项为0；R为计算时段内所产生的的地面径流量，mm；D为计算时段内深层渗漏量，mm，文中取该项为0；j为土壤层次号；n为土壤分层，根据TDR 的测试情况，以10 cm为间隔，共分为13层；Hj为第j层土壤的厚度，cm；θj为第j层土壤的体积含水量，%；R=α P，为径流系数，根据试验区测试数据确定。

2 ET值预测模型的构建

2.1 条件的概化

首先，假设田间土壤、植物、覆盖层、大气条件等均匀。假定非饱和土壤水为忽略侧向水分交换的垂直一维流，在垂直方向上，土水势连续。地表分为无积水层覆盖和有积水层覆盖两种情况。当地表无积水层覆盖时，降雨强度小于土壤入渗率（单位时间内通过单位地表面积渗入到土壤中的水分），此时的实际入渗率为土壤水分的补给速率；当地表有积水层覆盖时，降雨强度大于土壤入渗率，此时地表处于近饱和状态，实际入渗率为土壤入渗率。

2.2 水分运移的数学模型

土壤水分运移规律可以用对流扩散型非线性偏微分方程（组）来描述，其中只有少数方程在特定的边界和初始条件下可以得出解析解，而大多数方程不存在解析解。土壤水分运动遵循达西定理，由达西定理和连续方程可以推导出土壤水分运动基本方程[14]：

式中：θ为体积含水量，%；z为垂直坐标（从地面算起向下为正）；t为时间，min；D(θ)为扩散度，cm2/min；K(θ)为水力传导度，cm/min；l为计算深度，cm。

初始条件：初始含水量已知，即：

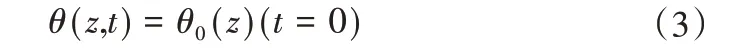
边界条件：

（1）上边界条件，当膜上无积水时：

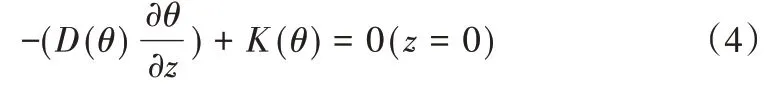
当膜上有积水时：

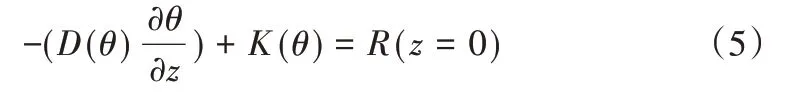
（2）下边界条件：

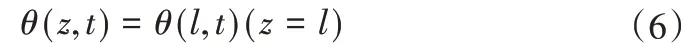
综上所述，一维土壤水分运动的数学模型方程可以用如下方程组描述：

为克服数值弥散的影响采用Bresler 算法，将土体按照垂直方向剖分为n个单元土层，空间步长为dz，节点编号为0，1，2，…，n-1，n，在dt（tk-1～tk）时间段内，对任一内节点i所代表均衡区（i-1/2）到（i+1/2）之间的土体上采用二阶差分近似的差分格式，可得土壤水分运移的节点方程组，通过两者的联合求解，就可得到任意时刻土壤水分分布情况。

2.3 数值计算过程及相关参数的计算

土壤水分数值模拟的计算可以采用以下步骤：①根据实测土壤剖面含水量θ、土壤容重γ，用插值法给出剖面上各点的含水量的初始值；②求解水分运动方程，给出时段末（每月21日）各节点的土壤含水量分布情况，计算得到式（1）中W0-Wt值；③将P、M、R代入式（1）中，计算得到月度ET值。

程序计算中涉及到的相关参数包括土壤水力传导度K、土壤水扩散度D和土壤水动力弥散系数Dsh。拟合相关参数时所采用的经验公式与模型参数如表2所示。

表2 计算中所采用的经验公式及其系数Tab.2 Empirical formulas and coefficients used in calculations

3 结果与分析

3.1 试验区ET值变化特征分析

根据试验点的土壤含水量、气象等监测资料，依据水量平衡方程，可以计算得到各试验点月度ET值，进而得到15个测点的月度ET平均值（后文中简写为ET值）。图1是2018年、2019年项目区15 个测点月度ET平均值的变化特征图。从图1曲线可以看出：越冬期过后，ET值逐渐增大，4月底达到第一个极值；进入6月雨季之前，ET值缓慢减小，雨季之前达到最小值；进入雨季后，ET值逐渐增大，8月底达到最大值；雨季结束后，ET值逐渐减小。

分析认为，试验区域内主要为黄土，土壤入渗能力很大，加之雨季植被涵盖等，导致大部分降雨都渗入到下层土壤当中，由降雨产生的地表径流量很少，而区域内没有耕作等人类活动影响，水分很难渗入到观测区域以下的土层当中。这就导致影响区域内ET值变化的主要因素有两个，一是降雨量，二是土壤含水量。而土壤含水量的变化主要是区域内降雨和蒸发相互作用引起的，因此，区域内ET的变化特征和区域内降雨变化特征一致。表现为：越冬后ET值逐渐增加，进入6月的雨季之前，降雨很少，ET值逐渐减小；6-8月雨季到来，降雨增加，ET值逐渐也增大；雨季结束后，ET值又开始逐渐减小。2018年度的测试数据显示，8月初之前ET值出现了一个低值，可能是两个年度降雨过程不完全一致引起的。结合两个年度的降雨过程，2018年度降雨7月和8月较为平均，土壤干湿交替时间短、次数较为频繁，导致雨季当中ET值产生波动；而2019年度降雨主要集中于7月底到8月之间，干湿交替时间长、次数较少，雨季中ET值波动并不显著。

3.2 坡向对ET的影响分析

以正南方向为0°，南偏西方向按照顺时针方向计算各测试点的坡向，南偏东方向按照逆时针方向计算各测试点的坡向（负值），绝对值在90°以内的为阳坡，绝对值在90°以外的为阴坡。选择坡度相近的测试点分析不同坡向月度ET值变化特征，如图2所示。图中坡向最大的阴坡156°为1 号和9 号点测试数值的平均值（两点坡度相同、坡向相近），阳坡80°为10 号点测试数值，阳坡75°为11 号和12 号点测试数值的平均值（两点坡度相同、坡向相近），阳坡6°为13 号点测试数值，阳坡-6°为14号点测试数值。

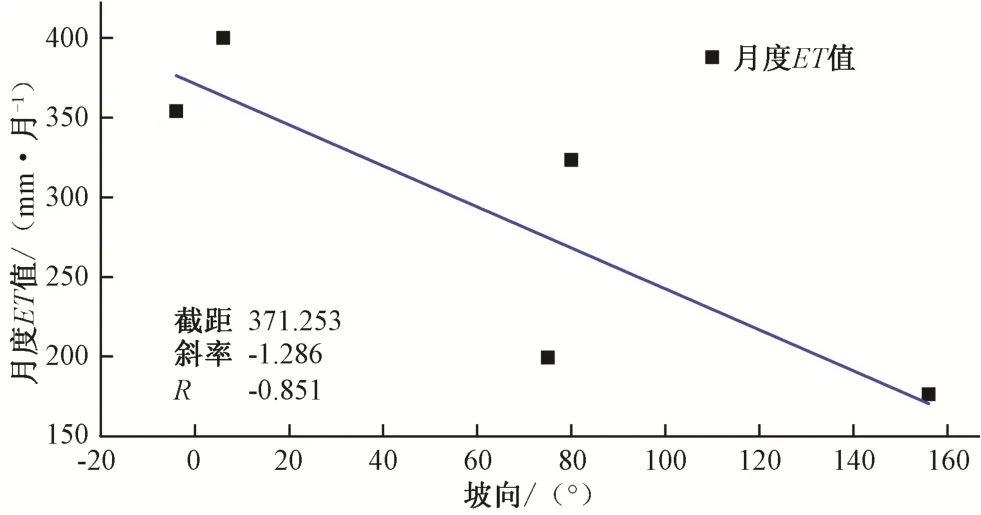
图2 试验区不同坡向月度ET值的变化特征曲线Fig.2 Variation characteristic curve of the month ET value of different slope directions in the test area

从图2结果来看，坡向和月度ET值之间有一定的相关性，而接近正南区域月度ET值为最大值。产生该现象的原因为：在其他条件相近的情况下，不同坡向就意味着接受太阳辐射的时长不同，月度ET值的大小和接受太阳辐射的时长相关，接受太阳辐射时长越长，土壤蒸发强度越大，月度ET值就越大；反之亦然。由于试验区地势开阔，没有其他遮蔽物，因而能够接受太阳辐射的范围较宽，下午的平均照射强度也要明显高于上午，阳坡接受太阳的照射时间也比阴坡相对较长，土壤蒸发强度相对较大，气温高，月度ET值就大；反之亦然。由于阳坡6°和阳坡-6°最为接近正阳坡，月度ET值为最大。

3.3 坡度对ET的影响分析

坡度分析时，以测试区地形平坡为0°，采用百分数表示地表测试的坡度。由于阳坡测点较少，文章选用阴坡面、坡向相近的测点，进行坡度单一变量对月度ET值的影响分析。在项目所在的区域内，图中坡度最小的3%为1 号和9 号点测试数值的平均值（两点坡向相近、坡度相近），坡度高之的27%为8 号点测试数值，坡度再高之的48%为2 号、4 号和5号点测试数值的平均值（三点坡向相近、坡度相近），坡度再高之的58%为3 号点测试数值，坡度最高的80%为6 号点和7号点测试数值的平均值（两点坡向相近、坡度相近）。图3为阴坡（1-11 号所在区域）测试期内月度ET值和坡度的相关变化特征曲线。

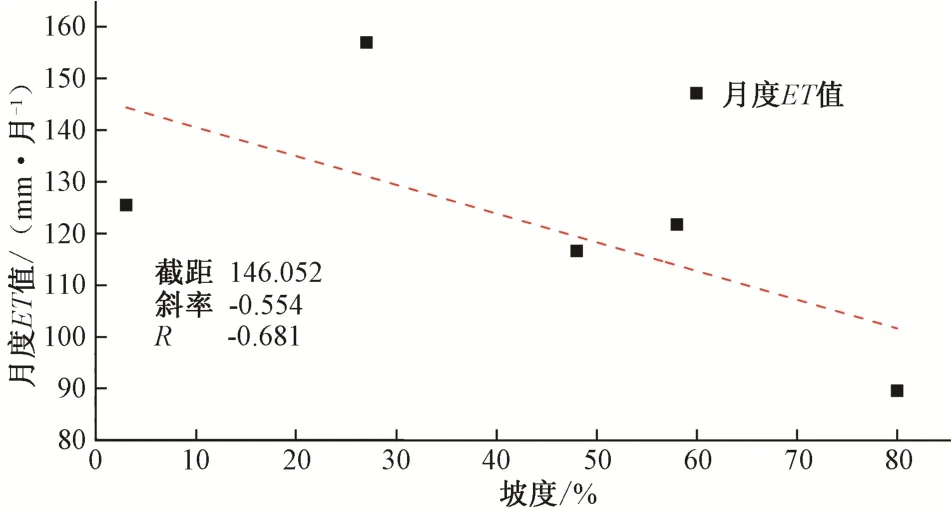
图3 试验区阴坡面（1-11号）不同坡度条件下月度ET值的变化特征曲线Fig.3 Variation characteristic curve of month ET value under different slope conditions of shady slope surface(1-11#)in test area

从图3数据可以看出：在其他条件相近的情况下，坡度越大，月度ET值越小；反之亦然。产生该现象的原因为：在其他条件相近的情况下，不同坡度意味着地表径流量不同，土壤入渗水量就不同，坡度越大，产生的地表径流量越大，土壤入渗水量就越小，土壤蒸腾蒸发量越小，月度ET值就越小；反之亦然。

3.4 模型的验证分析

根据试验点土壤基本特性，基于土壤特征曲线和水分运移模型，对土壤水分变化过程进行模拟计算，将模拟结果代入水量平衡方程后，可以得到该位置的ET值变化特征。计算所得各测试点不同时刻的ET平均值，结果如图4所示。结果表明，所构建的模型能够较好地拟合得到黄土丘陵沟壑区自然条件下不同辐射面ET值。

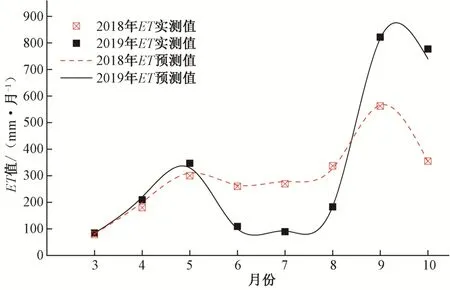
图4 试验点ET值数值模拟计算与实测值的对照图Fig.4 ET value numerical simulation calculation and actual measurement value comparison chart

4 结 论

本文以黄土丘陵沟壑区不同辐射面ET值为研究对象，在水量平衡法的基础上，构建了不同辐射面ET值预测模型。研究结果表明：①ET值在越冬期过后，逐渐增大，4月底达到第一个极值；进入6月雨季之前，ET值缓慢减小，雨季之前达到最小值；进入雨季后，ET值逐渐增大，8月底达到最大值；雨季结束后，ET值逐渐减小。②坡向和月度ET值之间有一定的相关性，接近正南区域阳坡的ET值为最大值；坡度和月度ET值之间也有一定的相关性，坡度越大，ET值越小，反之亦然。③采用水量平衡法对研究区蒸发蒸腾量进行预测，从模拟结果来看，所构建的模型能够较好地得到研究区ET值。