椭圆山岭隧道洞口段在SH波作用下三维动力响应
2022-04-13王振宇阳军生王星华
王振宇,阳军生,王星华
(1.中南大学 土木工程学院,湖南 长沙 410075;2.湖南财政经济学院 工程管理学院,湖南 长沙 410027)
我国地域辽阔,山地、高原和丘陵区面积占国土面积的60%以上。同时大部分山区(如青藏高原)又处于欧亚板块和印度板块挤压的接触带,是一个地震活动频繁的地带。随着我国西部大开发战略的深入进行,高速铁路的建设也正在(或即将在)西部山岭地区蓬勃开展,高速铁路隧道的抗震问题越来越引起人们的关注。隧道洞口段对于隧道来说是极为重要的组成部分,在地震作用下,隧道洞口段易发生破坏导致整个隧道无法正常应用。由于高速铁路的特殊性,其隧道结构形式大部分都采用双线单洞近似椭圆的结构形式,跨度比较大,断面的面积也比较大,使得隧道的洞口段更加容易受到地震的影响而破坏[1-5]。
隧道洞口段的动力响应研究分为理论分析、数值模拟和振动台模型试验3种,目前国内外的研究主要集中在数值模拟和振动台模型试验这2种方法,主要的研究内容是洞口段的减震措施和减震效果。这类研究主要考虑的是隧道洞口段单一横截面结构的动力响应,没有考虑隧道的整体性和波形传播的立体性[6-8],文献[9-10]仅仅考虑了在SH波作用下圆形山岭隧道洞口段的动力响应特征,并用椭圆隧道模型进行振动台试验来验证理论解析解的正确性。
隧道洞口段和隧道洞身的最大区别在于:隧道洞口段有一个凌空面,而隧道洞身段可以看作无临空面的结构,文献[11-18]根据波动理论和洞口有临空面的特点,将经过坡面反射的波在隧道结构中轴线上叠加,形成复杂的波场,这使得隧道结构的受力方式更加复杂。
本文将山岭隧道洞口段模型简化为单面坡简单结构,并认为隧道结构形式不影响波的传播,应用弹性波传播理论,推导了SH波从隧道底部垂直入射时椭圆山岭隧道轴线上的动应力响应规律。然后将椭圆隧道结构看成三维的薄壁壳结构,求解SH波作用下的隧道结构位移的解析解。最后根据前面的理论推导对山岭椭圆隧道进行振动台的模型试验,来验证前面理论分析结果的正确性,以总结椭圆山岭隧道洞口段变形机制。
1 理论推导
为了分析椭圆山岭隧道洞口段的动力响应特征,先假定山体中不存在隧道,仅考虑SH波从山体底部垂直入射时,经山体坡面反射时的效应,求解此时在隧道结构轴线处SH波反射所产生的应力场分布;在将隧道简化为三维薄壁壳结构的同时忽略围岩与隧道之间的相互作用,最后求解这些应力场作用下隧道结构的位移分布。
1.1 基本假设
上述理论推导过程遵循以下基本假设:
(1)围岩山体尺寸与隧道结构尺寸之间的比值大到可以忽略隧道结构的存在对围岩动力响应的影响。
(2)围岩与结构之间连接紧密,没有相对位移。
(3)将高速铁路近似椭圆的隧道结构简化为标准的椭圆结构。
(4)假设所有的结构均为均质弹性体,并且仅考虑单面坡的反射作用而不考虑散射作用。
1.2 椭圆形模型隧道轴向位移解析解
图1为单面边坡模型,由波动传播理论得:SH波从底部垂直入射,经路线O1B到坡面B点,发生反射,反射波沿路线BA到点A处,然后与直接经路线O2A入射的SH波叠加在隧道轴线的A点处,见图2。
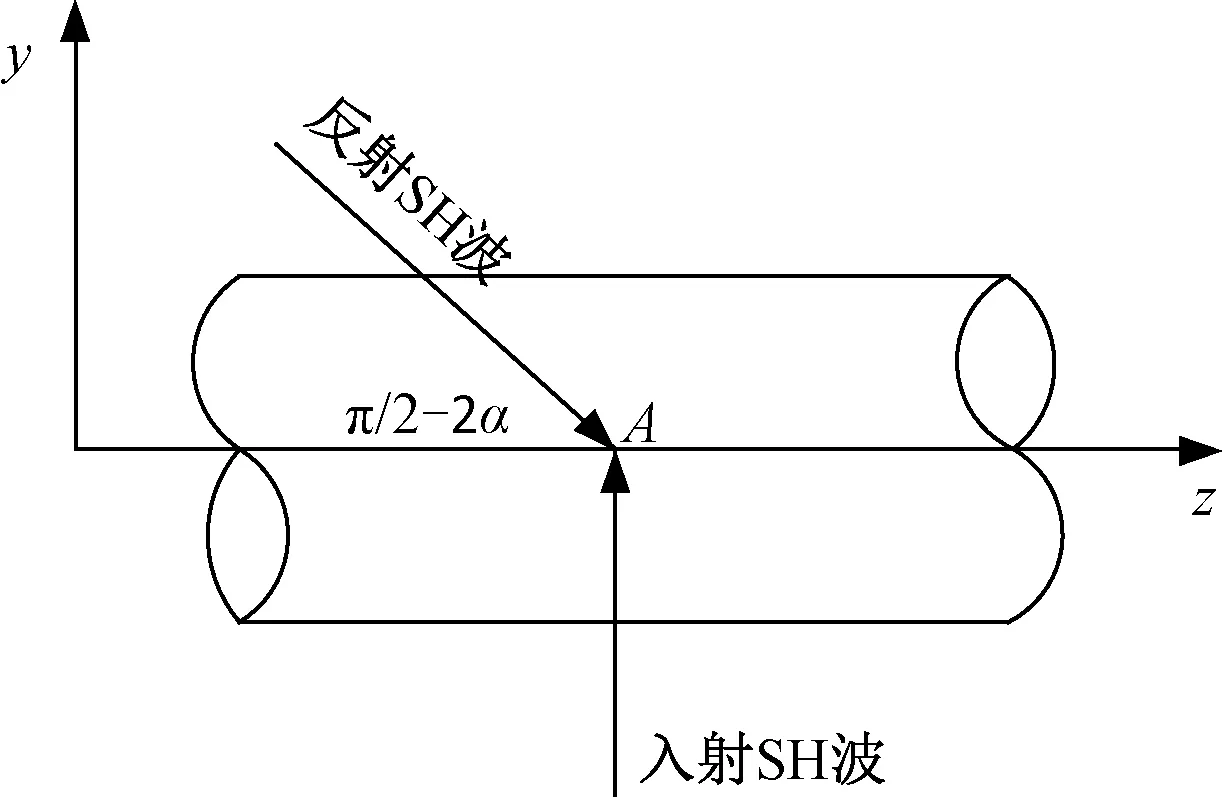
图2 轴向位移在A点叠加示意
根据波动传播理论,SH波的反射角α等于单面边坡的坡角α,入射波速等于反射波速,两者振幅相等[19]。
设入射波的位移函数为
(1)
式中:A0为振幅;L为波长;vs为剪切波速。将单面坡面看作自由边界时,反射波位移函数为
(2)
式中:t′=t-t0,t0为SH波从点D经坡面反射到达点A的传播时间(图1)。
根据图1的坐标系统,坐标原点为C点时,A点坐标为(0,z),则反射波到A点时间延迟为
(3)
根据文献[20]的研究,经山体坡面反射的SH波等效为如下两条波:沿隧道轴向(z向)传播的SH波,波长为L/cos(π/2-2α),波速为vs/cos(π/2-2α),振幅为A0;沿横截面方向(y向)传播的SH波,波长为L/sin(π/2-2α),波速为vs/sin(π/2-2α),振幅为A0。
所以,在A点处波场为上述3条波的叠加(入射SH波,沿轴向与横截面方向传播的SH波)。
为了求解隧道结构的动力响应,将隧道简化为薄壁椭圆柱壳体,应变的规定见图3。由于薄壁椭圆柱壳体横断面的厚度很小,所以只需考虑结构的轴向应变、环向应变、切向应变等3种应变。

图3 薄壁椭圆柱形壳体的隧道衬砌应变
轴向应变、环向应变、切向应变的计算式分别为
(4)
(5)
(6)
在柱坐标系中,椭圆方程为
(7)
(8)
式中:r(θ)为椭圆半径;2a、2b分别为椭圆隧道的长轴和短轴;uz、uθ、ur分别为柱面坐标系下剪切波所产生的位移分量。
故在上述叠加位移场作用下,隧道结构总应变等于每个波单独作用下所产生应变的叠加,下面对A点处3个波所引起的隧道结构应变分别进行计算。
椭圆的柱坐标系见图4。
根据图4坐标系,高速铁路双线单洞结构物X点的坐标满足
(9)
(10)


因此
(11)
(12)
1.2.1 沿隧道轴向(z向)传播的反射SH波
反射SH波沿z向传播在xOz平面内的运动,由围岩传递作用到隧道结构上的位移表示为
(13)
根据图4的柱面坐标系,将隧道位移进行分解,切向和径向的位移函数分别为
(14)
(15)
将式(14)、式(15)代入式(2)~式(4),经计算、整理可得到应变表达式为
(16)
式中:
A1=1/(ab)
(17)
(18)
(19)
(20)
(21)
1.2.2 沿y向传播的反射SH波
沿y向传播的反射SH波对应的位移函数为
(22)
同上,沿切向和径向对位移函数进行分解可得
(23)
(24)
将式(23)、式(24)代入式(2)~式(4),经计算、整理可得应变表达式为
(25)
式中:
(26)
(27)
(28)
1.2.3 沿y向传播的入射SH波
沿y向传播的入射SH波对应的位移波函数为
(29)
沿切向和径向对波的位移函数进行分解可得
(30)
(31)
将式(30)、式(31)代入式(2)~式(4),经计算、整理可得到应变表达式为
(32)
式中:
(33)
将以上3条SH波所引起的隧道结构应变进行叠加,并消去时间项t′,整理后隧道结构的总应变为
(34)
从式(34)可知,在底部垂直入射SH波的作用下,隧道结构的轴向应变为0,环向应变则是由沿y轴(平行横截面)方向传播的SH波所产生,切应变则是由沿z轴方向(轴向)传播的SH波所产生。
式(34)为椭圆山岭隧道洞口段的总应变表达式,当隧道结构为圆时(即长短轴相等),式(34)退化为文献[9]的形式。
2 椭圆形山岭隧道洞口段结构动力响应的影响因素分析
为了能够分析影响山岭隧道洞口段结构动力响应的各个因素,先假设基底入射的SH波位移函数为
u(t)=A0sin(2πft)
(35)
式中:频率f取2 Hz;振幅A0取0.3 m;t为时间,s。根据式(34)和式(35)即可计算出椭圆隧道结构动力应变响应的具体数据。
为此计算参数取值如下:椭圆隧道的长轴2a=11.2 m,短轴2b=8.6 m,厚度为0.48 m,围岩与衬砌参数见表1,隧道轴向方向取值100 m(z=100 m)作为研究范围,洞门角度取值70°,以便于与振动台模型试验结果进行对比。

表1 隧道衬砌与围岩的物理力学参数
SH波从隧道底部入射时,山岭隧道洞口截面各个位置的切向应变曲线见图5。由图5可知:隧道洞口截面各个位置的切向应变曲线均类似一条正弦曲线,这条曲线的振幅与山体坡度密切相关,如山体坡度为45°时,应变曲线振幅最大(处于拱底和拱顶位置,其绝对值相等但符号相反,ε=6.283×10-6),左(右)拱腰处应变值为零,应变曲线以隧道轴心为中心、左右对称、上下镜像对称;山体坡度为70°时,应变曲线反相,但最大应变依然是在拱顶和拱底位置,拱腰的应变还是为0。

图5 洞口截面的切向应变
考虑长短轴之比的影响时,隧道拱顶切向应变与山体坡度的关系曲线见图6。由图6可知:山体坡度为45°时,拱顶切向应变最大,随着山体坡度的增加,切向应变逐渐减小,在50°~60°之间,拱顶应变由正值转变为负值,山体坡度继续增加时,拱顶切向应变绝对值随之而增大,增大到极值以后,切向应变绝对值逐步减小,山体坡度为89°时,切向应变减小为0。从图6还可以看出:拱顶的切向应变不随椭圆长短轴之比的变化而变化,不同长短轴比时基本上是一条曲线,这说明长短轴之比对拱顶的应变几乎没有影响。

图6 不同a/b时隧道拱顶切向应变与山体坡度的关系
山体坡度为70°时,隧道不同截面切向应变与洞口距离的关系曲线见图7。由图7可见:这些切向应变曲线都以隧道中心为对称中心,左右对称、上下镜像对称;在距洞口100 m的范围内,各切向应变曲线相位发生了4次转变,最危险的位置仍然是拱顶和拱底,最危险的断面是距洞口100 m截面,最大应变绝对值为3.777 8×10-6,其正值出现在拱底,负值则出现在拱顶;次危险断面是距洞口5 m截面,拱顶的应变为-3.631 1×10-6。

图7 切向应变与隧道洞口距离的关系(α=70°)
距洞口5 m截面、长短轴之比(a/b)为1.1时,不同山体坡度隧道拱顶切向应变的时程曲线见图8。从图8可以看出:这些时程曲线在计算范围(4 s)内,振幅是稳定不变的,山体坡度不同时,其振幅是不同的,其频率(0.875 Hz)小于所输入地震波的频率(2 Hz);山体坡度为45°的时程曲线和70°的时程曲线刚好反相,但他们的频率是相同的。

图8 拱顶切向应变的时程曲线(a/b=1.1)
3 大型振动台试验模型的制作
为了验证理论分析的正确性,我们进行大型振动台试验来还原现场工况,对理论分析进行对比。为了能客观真实地探究原型的特性,采用缩尺的物理模型进行试验时,需要进行相似设计,模型试验物理量量纲的相似关系见表2。

表2 振动台模型试验物理量量纲的相似关系
3.1 椭圆形隧道模型制作和监测方案
根据振动台台面尺寸及其极限承载能力,设计模型箱尺寸为9 300 mm(长)×3 700 mm(宽)×2 500 mm(高),模型箱总重为38 kN。椭圆隧道衬砌模型见图9。

图9 椭圆隧道衬砌模型(单位:mm)
在隧道模型试验中,沿隧道轴向方向上,监测断面布置在Ⅶ-Ⅶ、Ⅵ-Ⅵ、Ⅸ-Ⅸ节段的中间位置,山体坡度为70°。椭圆形隧道洞口段纵断面剖面和底面俯视图见图10。

图10 椭圆形隧道洞口段纵断面剖面和底面俯视图
3.2 模型试验结果分析
对于不同的地震烈度,隧道结构应变的规律基本上一致,隧道洞口段结构环向应变的变化曲线见图11。

图11 隧道洞门内部环向应变f=7.237 Hz(单位:10-6)
由图11可见,输入正弦地震波,地震波频率不同时,其动力响应特征也不相同,最危险的部位是拱顶和右拱脚。由图11(a)可见,地震频率为4 Hz时,最大应变出现在拱顶(加速度为0.30g,应变为5.127×10-5);由图11(b)可见,地震频率为 7.237 Hz时,应变最大值出现在右拱脚(加速度为0.30g,应变为4.639×10-5)。
输入正弦地震波时隧道拱顶外部的纵向应变曲线见图12。由图12可见:随着地震加速度的增加,隧道的应变也增加,这个规律与所输入地震波的频率无关。当地震波的频率比较小时(f=6.383 Hz),隧道的应变随着距洞口的距离增加而增大;频率比较大时(f=13 Hz),隧道的应变仍然随着距洞口的距离增加而增大,但最危险的断面是距洞口35 cm处。在隧道轴向地震波的作用下,隧道将产生水平剪切变形,这些变形是沿着隧道轴向产生的;并且洞口段将产生较大的刚性位移,在右拱肩和右拱脚处容易产生破坏见图13。
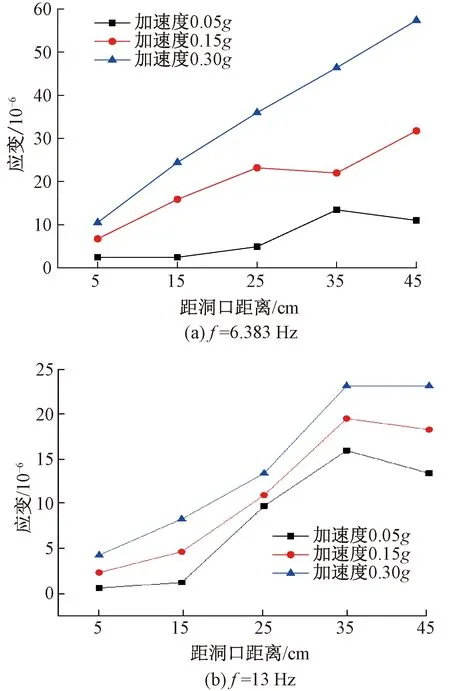
图12 隧道拱顶外部纵向应变曲线

图13 隧道洞口段右拱肩、右拱脚破坏图
以上试验结果初步验证了理论分析结果:山岭隧道洞口段容易发生破坏的部位通常是拱顶(底)和拱脚(肩)处,最危险的断面通常在距洞口35 cm处。
4 结论
本文在隧道底部垂直入射SH波的作用时,对椭圆山岭隧道洞口段的应变进行了模型的理论简化与推导,并进行了大型振动台的模型试验,通过分析两者的结果,得到如下结论:
(1) 将山体坡面简化为单面坡,获得底部垂直入射SH波时椭圆山岭隧道洞口段应变场的解析解,通过参数分析,认为:在输入正弦SH波时,椭圆隧道洞口截面各个位置的切向应变曲线以隧道中心为对称中心,左右对称、上下为镜像对称,拱顶和拱底应变最大,两者绝对值相等、符号相反,而左右拱腰的应变为0。
(2) 通过参数分析得出:随着椭圆长短轴之比的增加,隧道拱顶的切向应变不受影响,但不同山体坡度对切向应变有很大影响,如山体坡度为45°时,其应变最大为6.283×10-6,山体坡度为70°时,其应变为-3.631 1×10-6;最危险断面是距洞口100 m截面、次危险断面是距洞口5 m截面,拱顶(底)是最危险部位。
(3) 山体坡度不同时,拱顶切向应变时程曲线的振幅、相位不相同,坡度相同时,其振幅和频率是相同的;山体坡度70°的时程曲线与山体坡度45°时程曲线的相位相反,刚好相差180°。
(4) 通过大型振动台的模型试验,证明了理论模型的合理性与正确性,模型试验表明:隧道洞口段最危险的位置是拱顶或右拱脚,地震频率不同时,最危险的位置也不同,如:频率为4Hz时,最危险位置是拱顶(0.30g,5.127×10-5);频率为7.237 Hz时,应变最大值出现在右拱脚(0.30g,4.639×10-5),试验模型破坏结果也证实了这个结果。
(5) 将动力响应看作隧道横截面与纵向两个方向上动力响应的叠加,横截面上容易发生剪切变形,使得隧道两侧拱肩与拱脚为抗震的薄弱环节,这种现象会沿轴向缓慢增加,系平行隧道结构横截面传播的SH波所致。
以上结论可以作为山岭隧道洞口段设计与施工的参考依据:洞口5 m范围内增强衬砌强度、加强拱顶位置衬砌的刚度与强度是保证隧道安全的有效手段。
