不同流速对隧道排水管结晶规律室内试验研究

熊 帅

(内江师范学院 人工智能学院，四川 内江 641100)

1 引言

随着我国地下轨道交通、高铁事业的深入发展，地下空间渐渐被大量开发。当前我国的隧道数量已居世界第一，成为了隧道大国[1]。川藏铁路东起四川省成都市，终于西藏自治区拉萨市，途经雅安、康定、昌都、林芝、山南等地。其中，成都到雅安段于2018 年开通运营，而从雅安到林芝段估计新建隧道总长约953 m，桥隧比高达93%，由此可见其隧道、高海拔隧道、隧道群以及特长隧道占比之大，工程勘察、设计、施工、运维面临巨大挑战[2,3]。

隧道，尤其是一些高等级公路隧道[4,5]，要求洞内环境干燥无水，对防排水技术要求很高。早期所修隧道因排水不当引发的隧道结构[6]问题层出不穷，归根到底大多未做防水措施，在20世纪60年代以前表现得尤为严重。近年来一些新建的隧道，也存在较严重的渗透漏水[7,8]。由于隧道排水不当轻则引发营运期间的涌突水等，重则引发隧道结构变化，威胁隧道正常运营，这些问题严重阻碍了隧道事业的进一步发展，成为公路工程中的十大通病之一。因此解决隧道渗水所引发的隧道漏水、涌水[9,10]等一系列问题已经成为工程设计与工程施工中的一个关键技术环节。

因此，本文依托科研项目对西南片区隧道现场进行调研，总结了导致隧道排水管堵塞的物理、化学、人为的内外在因素，并通过室内实验装置研究了5种不同流速对排水管堵塞的规律(图1)。

图1 现场排水管堵塞物

2 隧道排水管堵塞因素

(1)物理因素[11～14]。空气中存在大量的CO2，和

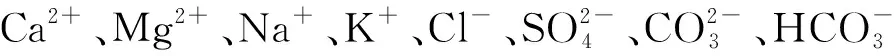
MgCO3+Ca2+→CaCO3+Mg2+

得出沉淀物CaCO3、CaSO4、MgCO3、MgSO4等在化学键的作用下附着在管壁内侧不能及时在水流作用下排出，最终导致排水系统堵塞[16]。

(3)人为因素。管道设计时，通常根据隧道断面情况、行车辆大小、排水量大小等进行设计。因此，如果调查人员在勘察设计阶段存在疏漏，排水管管径设计偏小，那么在雨季时，周围的泥沙、生物残骸等不能及时排出管道，引起管内堵塞，破坏管壁；若排水管管径设计偏大，相应的过水断面面积加大，水流速度会降低，微溶于水的钙化物、镁化物会沉淀附着在管壁内侧，不易排出管壁，形成晶核，如此恶性循环，导致排水系统失效。在实际施工过程中，也存在施工人员操作不当导致管壁埋设的设计坡度与实际坡度差别较大，根本原因是操作人员未依据设计图纸、标高的测定、施工中人为误差等。且管道安装施工完成后由于管壁内侧有一些泥沙残渣烂叶没有得到及时疏通等因素也会造成隧道排水管排水不畅，引发堵管的情况。

隧道排水管堵塞原因还有很多，除了上述的物理、化学、人为三类因素外，还包括气温高低、当地气压、溶液酸碱度等因素。隧道排水系统是隧道建筑结构的重要组成部分，一旦发生破坏，会造成隧道结构的损害，二衬开裂威胁行车安全。因城市地下空间隧道渗水导致的隧道结构病害问题，后期工程维修需要大量的资金，甚至有的维修资金超过了建造投资；一些漏水严重的地区导致大量涌水已经发生交通事故，严重威胁到人们的行车安全和生命财产，因此可见隧道排水的重要性。通过现场调研发现，受不同地势的影响，各排水管道水流速度不尽相同，排水管道堵塞受不同水流速度的冲击程度也不一致，后文将采用室内模型试验方法对不同流速因素影响管道堵塞规律进行研究。

3 试验装置

实验采用两个循环水箱的模型尺寸均由60 cm×30 cm×30 cm(长×宽×高)水箱进行联通形成一个单缸循环系统，利用水泵将循环液体抽入不同实验要求的管径中，排水管道的内径为32 mm的PVC管，通过流量计控制不同实验的流速，使溶液经过不同时间段的实验管道，通过不同时间段对实验管段的烘干称重判断结晶的速度和质量关系(图2、图3)。

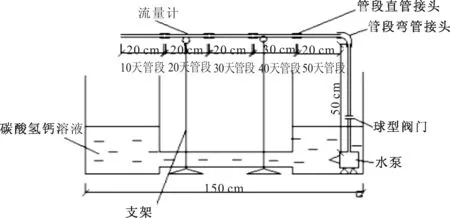
图2 水缸立面

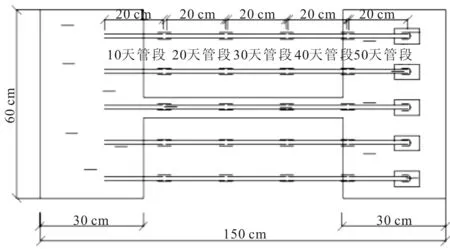
图3 实验装置平面

3.1 实验溶液配制

采用化学试剂NaHCO3和CaCl2按2∶1的比例，加入水配备，在配备溶液时由于CaCl2溶于水会放热，故应先加入，再加入NaHCO3，边加边搅拌，让其充分反应，保证比表面积接触充分，静置24 h后，取上层澄清溶液进行实验。

3.2 实验参数选择及其他因素的控制

实验一共使用50根实验管段，统一选取PVC管径为32 mm的管道，实验管段的长度设为20 cm，分为5 组。每组在不同流速作用下进行实验研究，最后对每组结晶量取平均值，然后对5 种不同流速作用下结晶规律进行对比。实验室温度通过空调控制在25 ℃。

3.3 实验具体布置

第一批将25 根实验管段同时安装在溶液箱的接口上，分别对每根管段进行编号，使5 组管段的水平高度统一，确保每根管段的初始流速相同的。实验每隔10 d进行称重一次，第一次称重取下第10 d称重管段，第二次称重取下第20 d称重管段，……，依此类推，最后一次取下第50 d称重管段，此时第一组实验结束，50 d为一个周期，同一组的管道结晶量进行对比和观察，然后两组取平均值，减小误差，最后得出实验值进行分析。

3.4 实验及计算步骤

(1)截取25 根长度为20 cm的管段，实验管段直径统一为32 mm，25 根为一组，分为两组。给每组的每根管子编号且称重，精确到0.001 g，并认真做好记录。

(3)将调试好正常运行的实验仪器于常温下，打开管道的阀门，开始循环。

(4)每隔10 d测一次管道干重，将测得的数据减去原始管道的重量，就得出不同管子结晶的重量，如实记录每个数据。

(5)50 d之后，实验结束，清理容器和其他仪器，做好保养工作，以备下组实验使用。

(6)计算得出两组管段的不同数据，取平均值，得出管径为32 mm的管子内部的结晶量，把实验数据如实的记录在表格内。

4 结果及分析

试验结果如表1。

表1 不同流速组结晶量 g

根据以上实验数据，得出如下曲线(图4、图5)。

图4 不同流速实验管道结晶质量与时间关系

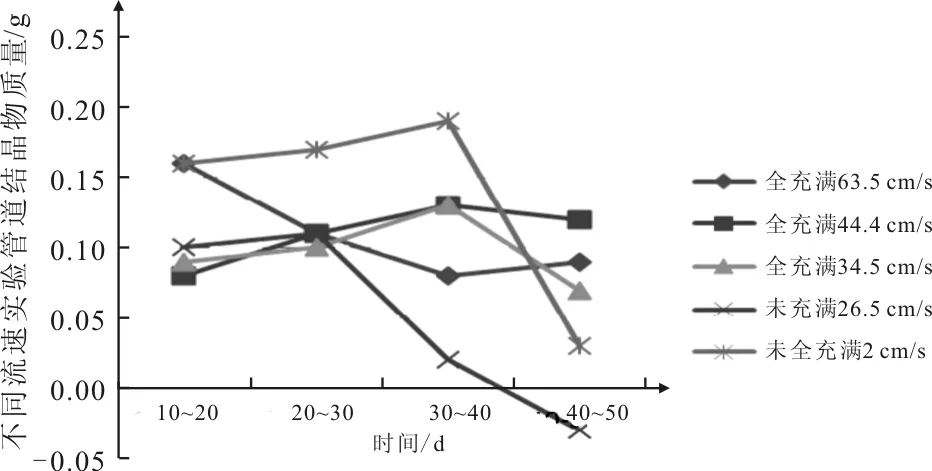
图5 不同流速实验管道结晶增量与时间关系

表1结晶量是根据实验管道前后质量之差计算得出，结晶增加量是根据相邻两管道之差算得出，分别反映了结晶量和结晶增量与时间的关系。图4反映了流速较慢的实验管道即未充满水的管道比全被溶液充满的实验管(流速快的)道结晶速率要快、多。其中，在管道未充满情况下：流速为22 cm/s时，结晶量最大值与最小值之差为0.55 g；流速为26.5 cm/s时，结晶量最大值与最小值之差为0.23 g。在完全充满管道的情况下：当流速为34.5 cm/s时，结晶量最大值与最小值之差为0.39 g；当流速为44.5 cm/s时，结晶量最大值与最小值之差为0.44 g；当流速为63.5 cm/s时，结晶量最大值与最小值之差为0.44 g。其次受流速的影响，各个不同流速的管段结晶量均先呈现上升的趋势，随着时间的推移在后期均达到饱和状态，保持平稳，结晶速率减缓、减慢，管道初期在与碳酸钙晶体之间的相互作用力较强，大量附着在管壁上慢慢导致溶液中的杂质堆积，后期不再是以碳酸钙晶体与管壁之间相互作用力为主导，其作用渐渐减弱，并且后期管壁的沉积物被水流冲击磨圆，所以质量变化很小。从图5 中可以看出，5 种流速中只有一组出现了负增长的现象，是在流速为26.5 cm/s时，负增长值大小为0.03 g，数量级为0.01 g，相比在流速为26.5 cm/s，实验结晶量数量级1 的基础上，其增量其实较小；其次，在流速较快的管道处，结晶变化幅值波动比较大。

5 结论与展望

在对以重庆为代表的的中梁山隧道和以贵州为代表的大山隧道实地勘察调研的基础上，综合考虑了纬度、经度，隧道建设地势，隧道运营周期，运营过程中隧道内的排水管道内水流速度的变化等，建立室内试验模型，研究流速对管道结晶规律的影响。通过对比不同流速下，结晶量及结晶增量两个指标的不同，得到以下结论。

在未满管或水流速度较慢时，由于溶液中杂质的沉积和晶体结晶物与管壁的相互作用，其结晶量和结晶速率较大。其次在各不同流速之间，结晶量的增长率都有先高后逐渐趋于平稳的趋势；管道未充满情况下：流速为22 cm/s时，结晶量最大值是最小值的1.83 倍；流速为26.5 cm/s时，结晶量最大值是最小值的1.32 倍。在完全充满管道的情况下：当流速为34.5 cm/s时，此时最大值是最小值的1.8 倍；当流速为44.5 cm/s时，结晶量最大值是最小值的2.83 倍；当流速为63.5 cm/s时，结晶量最大值是最小值的2.69 倍。

本文研究了流速对管壁结晶的影响规律，坡度因素实质上也可归结到这一研究中，根据重力势能的理论换算公式，如果存在一定的坡度为α，则有P=mghsinα，可以和动能进行换算，进而在对流速的研究显得十分重要。

本文的不足之处在于周期较短，不能完全模拟大自然四季交替变化对隧道管道堵塞的变化规律，另外本文主要是从室内试验宏观层面进行模拟，建议在后期研究水流速度与管壁结晶规律时加入一定的微观动力学模拟，将两者进行对比，能从更加深层次了解反应堵塞机理。