中国网络人口区域分布的影响因素分析——基于面板向量自回归模型

祝长华，谢俊贵，李少勇，吕玉文

（1.韶关学院 数学与统计学院，广东 韶关 512005； 2.广州大学 经济与统计学院/社会创新研究中心，广东 广州 510006）

中国互联网信息中心（CNNIC）是负责中国域名注册和互联网统计的准政府机构，于1997年开始发布有关中国网络人口（以前称为互联网用户）的统计信息.仅20多年，中国的网络人口就从62万增长到9.89亿（截至2020年12月31日），占中国总人口70.4%.伴随这一飞速发展的同时，网络人口的区域发展非常不平衡，例如，2016年，北京网络人口普及率达到77.8%，而云南仅为39.7%.在数字经济时代，网络人口是数字经济的生产者和消费者.一个省网络人口的发展水平会影响它在国民经济中的潜在地位.

网络人口研究一直受到重视［1］.早在2000年，美国就在“调查数字未来”调查中对网络人口进行了定量分析.网络空间具有社会的特征，可以称为网络社会［2］.因此，可以将Internet用户称为网络人口.谢俊贵提议建立网络人口统计学［3］.现有文献中有关中国网络人口区域分布的决定因素主要有：经济因子、电信设施建设水平、教育发展水平、科学和技术发展、总人口、城市化水平等.其中，陈扬乐发现区域经济的发展水平，城市化率，信息基础设施和教育水平是影响中国网络人口区域分布的因素［4］.但当时中国网络人口的发展还处于起步阶段，且忽略了时间的影响以及各省之间的发展差异.孙中伟等认为GDP和人口总数是关键因素，尽管总人口规模将影响Internet人口的发展，但如果仅将经济和总人口作为因素，则会高估总人口的影响［5］.虽然对中国网络人口区域分布影响因素的研究尚未深入，但学者们对互联网扩散和数字鸿沟的影响因素却进行了广泛的研究［6-8］.这些研究可以为本研究选择指标提供很好的参考.大多数学者对一些因素已经达成共识，其中最常见的是经济因素［9］.同样电信基础设施，特别是电话密度，也被认为是重要影响因素［10］；然而，在当前的移动互联网和宽带时代，选择电话密度作为信息基础设施建设水平的代理变量显然是不合理的.此外，教育也被认为是一个重要影响因素［11］.教育是全球信息技术传播的重要影响因素.最后，一个国家或地区对外开放程度，尤其是对外贸易开放程度，对技术扩散也具有重要影响，也是一个重要影响因素.

尽管先前的研究已经分析了多种因素，但它们却忽略了时间和个体差异的影响，这有可能会完全扭曲分析结果.而且，他们大多使用多元线性回归进行检验，这不能动态分析因素之间的动态变化.因此，有必要考虑使用因素、个体差异和时间的动态面板回归模型来分析中国网络人口区域分布的影响因素，以更好地解释中国网络人口的区域分布差异.文章采用面板向量自回归（PVAR）模型分析了中国网络人口的分布情况解释了网络人口与影响因素之间的互动关系，丰富了有关地区经济发展不平衡的影响因素研究，并能为数字经济发展提供参考价值.

1 数据和模型

1.1 数据和变量

研究调查了31个中国省市（不包括台湾，香港和澳门）的2001-2016年的年度数据.数据主要来自于CNNIC和中国统计年鉴（1998-2017）.为了避免异方差，对所有变量取对数.所有分析均使用Stata 12和Excel 2010进行.研究从经济发展水平、对外开放程度、教育发展程度和信息基础设施建设等几个方面分析影响因素.在参考前人研究基础上选取如下变量，见表1.

表1 变量列表

1.2 自适应权重面板聚类分析

面板聚类分析将多元统计方法应用于面板数据，很快得到广泛应用.本研究采用李因果等提出的自适应权重的面板数据聚类方法［12］.它综合考虑个体间的“绝对量距离”（dij（AQED））、“增长速度距离”（dij（ISED））和“变异系数距离”（dij（VCED））.设面板数据集为｛xitk｝，i=1，…，N；t=1，…，T；k=1，…，Q.其中Q为指标个数，T为总时期，N为个体数.选取因变量和自变量一起对样本进行分类.这3类距离的表达式分别为：

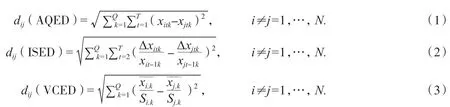
对dij（AQED）按照公式（4）进行标准化，得到标准化距离zdij（AQED），即：

同理，可以得到其它两个标准距离分别为zdij（ISED），zdij（VCED）.

再将它们代入式（5），即：

得到最终距离dij（CED），其中ω1，ω2，ω3为权重，可由熵权法得到.

设类GL和GK合并为新类GR，则其他类Gi与新类GR的距离平方为：

最后合并距离最小的两类，分类数由碎石图判断.

1.3 面板向量自回归模型

研究采用的面板向量自回归（PVAR）模型是由 Holtz-Eakin等于1988年提出的［13］.它综合了面板分析和向量自回归模型的优点，既能够控制不可观测的个体异质性（包含时间效应和个体效应），也可以分析面对冲击时变量的动态反应.与向量自回归模型相比，它对时间序列中时间的维度大大降低.本研究采用简化式PVAR模型，它的具体模型表达式为：

其中Yit是1×5的因变量向量，ui和eit是1×5的面板固定效应和随机误差向量.矩阵A1，…，Ap是5×5的待估参数向量.模型假设E（eit）=0，E（éit eit）=Σ，E（éit eis）=0，对任意t＞s.然而，PVAR 模型对变量的排序很敏感.因此，通常的惯例是，在系统中将更外生的变量排在前面，而更内生的变量排在后面.本研究假设变量按以下顺序：｛lnpinver，lnpgdp，lnpedu，lnpphone，lnpinter｝.

对模型（7）的处理和估计主要分为4个步骤：（1）模型诊断及估计.首先对各变量进行平稳性检验，否则会出现伪回归.文章采用常用的Levin等2002年提出的ADF检验［14］.随后按照信息准则选择模型，选择了滞后一阶的PVAR模型.最后，为了消除模型中个体效应和时间效应造成的系数估计偏差，采用截面均值差分和向前均值差分来分别消除时间效应和个体效应.这样保证了转换后的变量与滞后变量正交，从而可以将滞后变量作为工具变量进行估计.文章采用GMM方法对模型进行估计.由于模型中有许多待估参数难以解释，因此，研究者更感兴趣的是格兰杰因果关系检验、预测误差方差分解和脉冲响应函数图. （2）格兰杰因果关系检验.检验变量之间的因果关系.（3）预测误差方差分解.能够刻画模型中一个变量的冲击对其它变量波动的贡献度.（4）脉冲响应函数图.能够很好的隔离出一个变量的冲击对其它内生变量的影响.采用蒙特卡洛模拟500次得到脉冲响应函数标准误的置信区间.

2 结果分析

2.1 区域聚类分析

通过熵权法计算，绝对欧几里得距离，增量速度欧几里得距离和变异系数欧几里得距离的权重分别为0.302、0.271和0.427，可将省市分为4类.第一类包括经济发达但网络人口相对不多的省份（北京、天津和上海），例如北京，2016年，网络人口普及率达到77.8%.这一类型的网络人口普及率均超过70%.它们的经济发展水平较高，网络人口发展较早.但近年来，与其他省份相比，网络人口规模较少，而互联网普及率却很高.第二类包括经济发达而且网络人口规模也大的省份（江苏、浙江、广东和福建），例如广东省，主要位于东部沿海地区.这些省份的网络人口发展较早，并且近年来一直处于前列，网络人口普及率均超过65%.第三类包括经济和网络人口水平中等的省份（湖北、湖南、四川、山东、重庆、辽宁、吉林、黑龙江、河南、河北、安徽、江西、广西、内蒙古、山西、陕西、贵阳和海南），例如湖南.此类省份数量最多，主要集中在中部地区，网络人口普及率在55%左右.这些省份所有指标的发展水平均是中等水平，人口众多，网络人口也较大.又如，在河南，尽管网络人口普及率在中等水平，但是，近年来，网络人口规模却一直处于前列.第四类是经济和网络人口发展都落后的省份（云南、新疆、西藏、青海、甘肃和宁夏），例如云南，2016年网络人仅为39.7%.这些省各个指标都相对落后.

2.2 中国网络人口区域分布影响因素分析

所有变量在显著性水平0.05下均通过平稳性检验.在显著性水平0.1下，经济发展水平，教育发展水平和对外开放程度是网络人口发展的格兰杰原因，但是信息基础设施不是网络人口发展的格兰杰原因.另外，网络人口发展和教育发展水平互为格兰杰因果；网络人口发展与对外开放程度互为因果关系；经济发展水平和对外开放程度互为因果关系；经济发展水平与信息基础设施建设互为因果关系；信息基础设施与教育发展水平互为因果关系.这为中国的互联网+战略提供了理论基础.此外，教育发展水平是对外开放程度的格兰杰（Granger）原因；信息基础设施建设是对外开放程度的格兰杰原因.尽管格兰杰因果关系检验揭示了变量之间的因果关系，但该检验无法衡量这种关系的强度或样本时间以外的情况.预测误差方差分解可以用来度量各变量的扰动项对其它变量预测误差的单独贡献，即可以度量某个变量对另外一个变量的影响.所有变量对其它变量（包含自身）预测误差方差的贡献比例之和为1.

2.3 预测误差方差分解

PVAR模型的稳定性检验显示模型满足稳定性条件，这意味着结果可用于预测.表2给出了预测期数为1期和10期的预测结果.预测期数为1时，所有变量预测误差方差主要受自身的影响；在第10期，网络人口发展的变化42.5%由教育发展水平解释，26.3%由自身解释，其次是信息基础设施建设（14.5%）和经济发展水平（12.3%）.这一结果证明了教育发展水平对于网络人口发展的重要性.对外开放程度和教育发展水平的预测误差方差主要受自身的影响（分别高达78.9%和70.3%）.信息基础设施建设和经济发展水平的预测误差方差变化也主要受教育发展水平的影响，但相比来说比例较低分别为49.3%和37.9%.综上，教育发展水平对于网络人口发展、经济发展水平和信息基础设施建设均非常重要.

表2 预测误差方差分解结果

2.4 脉冲响应函数

脉冲响应函数用于分隔系统中变量的作用，分析一个变量纯粹受其他变量冲击的反应.脉冲响应函数的分析结果表明，网络人口发展对信息基础设施建设的响应为正，但影响越来越弱并最终趋于平稳.短期内教育发展水平对网络人口发展产生较强的负向影响，但很快回落.这可能是因为在后期学历较低的人是网络人口增加的主力军.起初，经济发展水平对网络人口发展产生了正向且强烈的影响，但后来逐渐消失.对外开放程度对网络人口发展的冲击不大，影响很小.信息基础设施建设似乎对网络人口发展的影响并不十分敏感.可能是因为信息基础设施的建设更多地取决于国家政策.从对信息基础设施的影响看，网络人口发展和教育发展水平对信息基础设施建设的冲击相对较大.从对教育发展水平的影响看，信息基础设施建设和经济发展水平对教育发展水平有持续的正向影响.网络人口发展对教育发展水平提升也有正向作用，但是最终会回落.从对经济发展水平影响看，信息基础设施建设对经济发展水平有较强的正向影响.教育发展水平对经济发展水平有负向影响.在样本期内，中国的教育发展迅速，但是它对收入的促进作用已减弱. 2005年，出现民工荒；大学生工资不如民工收入现象是一个迹象.从对对外开放程度影响看，经济发展水平和信息基础设施建设对对外开放程度的影响持续为正向影响.网络人口发展和教育发展水平对对外开放程度的影响短暂，最终将回落.

2.5 稳健性检验

交换相关系数较小变量的顺序对结果的影响较小［15］.笔者交换了具有较大相关系数变量的顺序，以评估模型的稳健性.在变量中，经济发展水平与网络人口发展之间的相关系数最大（0.993），其次是经济发展水平与教育水平之间的相关系数（0.989）.最后是网络人口发展与教育发展水平之间的相关系数（0.982）.通过交换这三对变量的顺序重新建模，共建立了三次模型.观察格兰杰因果关系，预测误差方差分解和脉冲响应函数图的变化（由于长度限制，结果未列出）.与原始模型相比，结果几乎没有差异.因此，该模型具有很高的稳健性.

3 结语

利用2001年至2016年31个省的数据，分析了中国网络人口的区域分布特征和影响因素，并采用面板数据聚类分析方法对31个省进行分类.进而采用PVAR模型对中国网络人口的区域分布的影响因素及因素之间的相互作用进行分析.结果表明：（1）中国网络人口区域分布不均衡呈现由东向西递减.这31个省市可以分为4类：经济发达，网络人口普及率高，但网络人口规模相对较少的省市；经济发达，网络人口普及率高且网络人口规模大的省市；经济发展水平和网络人口普及率均中等水平的省市以及经济落后和网络人口普及率低的省市.（2）对外开放程度、经济发展水平和教育发展水平都是影响中国网络人口分布的重要因素.（3）从长期看，教育发展水平将是网络人口发展、信息基础设施建设和经济发展水平的重要影响因素.（4）除了对外开放程度的冲击对其它变量的影响较小外，各变量的变动对其它变量均有一定程度的影响.这里重点关注到，短期内，教育发展水平对网络人口发展的负向影响，可能原因是当高学历人群的互联网普及率接近100%饱和时，网络人口的增长主要取决于教育程度低的人群.教育发展水平的冲击将导致网络人口在短期内为负向影响.

随着互联网对社会生活的深入渗透，网络人口的发展将影响地区的社会经济发展.因此，笔者提出一些建议，以期能促进我国网络人口和数字经济的发展：（1）地方政府应颁布各种优惠政策以吸引外国投资，并学习和引进先进的外国技术和设备，特别是信息技术产品.（2）在农村和西部地区，引导和鼓励企业和个体户与互联网融合，利用互联网不受时间和空间限制的优势，扩展销售市场以提高经济增长水平；降低互联网访问成本，特别是手机流量成本，并保证公共信息服务的最低数量和基本质量，将有利于网络人口的增长；一些网民建议将Wi-Fi视为最低需求水平，并提出了“新马斯洛需求理论层次”.（3）政府带头并鼓励非政府组织共同努力，为弱势群体提供资金和培训；在农村和西部地区建立信息服务站，并为普通民众提供互联网咨询服务和培训.（4）国家应加大对教育的投入，提高中国网络人口的素质.网络人口是高质量的资源，不能单纯追求数量增长.网络人口可以促进经济发展和社会进步.受过较高教育和收入的互联网人群倾向于将互联网用于经济利益，而那些社会经济地位较低的人群则主要将互联网用于娱乐活动.