基于遗传算法的城市水环境治理绿色施工优化

李 新 薛振宁 黄 健

(1.江苏建筑职业技术学院，江苏 徐州 221116；(2.徐州市水利工程建设管理中心，江苏 徐州 221000；3.徐州市水利工程建设有限公司，江苏 徐州 221006)

绿色施工是可持续发展思想在绿色理念中的一种体现[1]，早在20世纪30年代，巴克敏斯特·富勒就首先提出“少费而多用”思想[2]，即通过合理设计与利用，实现资源效用的最大化。据统计，建筑活动使用了人类使用自然资源总量的40%，能源总量的40%，而造成的建筑垃圾也占人类产生垃圾总量的40%[3]。在可持续发展的大背景下，绿色施工必然会成为工程行业的发展方向。

在绿色施工优化方面，王宇静等[4]建立了绿色施工多目标均衡优化模型，并采用先进仿生算法——微粒群算法(PSO)对模型进行求解；刘玲等[5]通过采用多属性效用函数理论对绿色建筑的工期、成本和质量进行分析，建立了多目标的综合优化模型；朱慧娟[6]将改进的粒子群算法运用到一个具体实例，求出了进度、成本、质量和环保的最优状态。

随着我国城镇化进程的加快和经济的飞速发展，中小河流开始出现水环境污染、水质恶化等问题。为满足人们日益增长的环境需求，打造生态宜居城市，绿色理念也相应地引入到中小河流水环境治理中，但基于该理念的绿色施工研究还比较少，对绿色施工的智能优化也不够完善。

1 绿色施工多目标管理

所谓绿色施工多目标管理，即是通过开展绿色施工优化研究，将先进的决策模型引入现代建造技术，以便优化施工安排及资源投入，保证施工进度，为工程建设提供更加科学合理的解决方案。在常规的费用、质量、工期的基础上加入绿色施工指标，将环保因素纳入施工主要控制目标中，并与费用、质量、工期等构成多目标控制系统。在均衡项目的进度、费用、质量和环保这四个目标之间关系的同时，确定最优目标，为企业决策提供依据。绿色施工与常规施工管理目标的对比见图1。

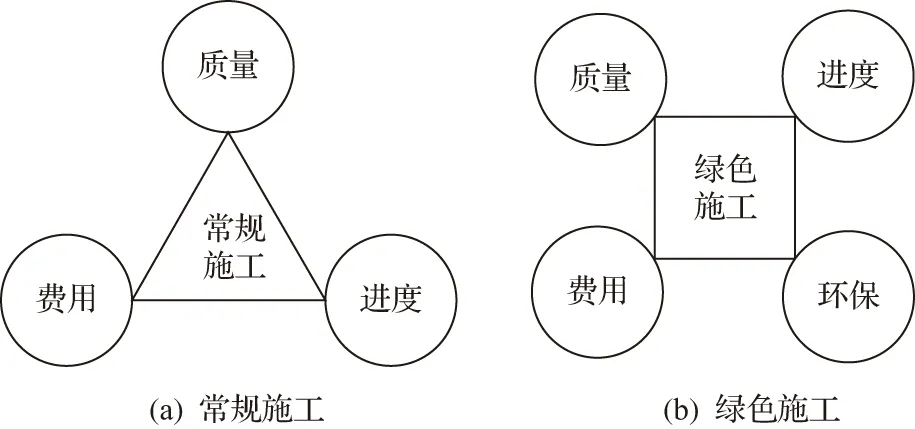
图1 管理目标对比

2 绿色施工多目标优化模型

在绿色施工管理中，质量、工期、费用、环保四个方面存在一定的内在联系，可以表示为线型关系[7-9]。由于水环境治理项目涉及的因素较多，采用线型关系存在一定的不足，本文结合工程特点，构建项目工期、质量、绿色施工水平与费用的二次函数关系。

2.1 工期和费用的关系

工程建设项目的费用，一般由直接费和间接费组成。直接费包括人工费、材料费、机械台班费、措施费等。间接费指无法直接计入工程成本，但为进行工程施工所发生的费用，包括管理人员工资、资产使用费、保险费等。在水环境治理项目中，要压缩工期则必须有更多的人员、机械、设备等的投入，从而导致直接费的增加；反之，相应的资源投入减少，则会导致工期的延长以及费用的减少；间接费一般随工期的增加而增长。对于一个特定的项目，费用一般随着工期的延长先下降后上升[10]。综合考虑直接费与间接费之后，可以得到工期与费用之间的函数关系：

(1)

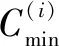
成本变化率a(i)可由下式计算得到

(2)

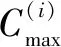
2.2 质量和工期的关系

在水环境治理中，为保持正常的质量水平，必须维持一定的时间投入，当投入的时间增加时，质量会有一定幅度的提升，但当质量水平达到一定程度后，工期增加对质量提高的影响便越来越弱，质量与工期的关系可表达为

(3)

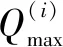
2.3 绿色施工水平和工期的关系

由于绿色施工是一个动态的过程，需要对环保、节能等进行持续投入，还需要对既有施工造成的非绿色因素进行治理，均需有一定的时间投入，绿色施工水平会随着投入时间的增加而提高；反之，压缩工期则会导致绿色施工技术不能得到有效应用，甚至会以牺牲环境为代价进行赶工。绿色施工水平与费用的函数关系可以表示为

(4)

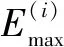
3 优化模型的建立

3.1 多属性效用函数关系

为了对绿色施工进行优化，需要对质量Q、进度T、费用C、绿色施工水平E四个指标进行统一分析，但由于在优化模型中，四个指标的单位不一致，需要对其进行归一化处理，构建的函数为

u=u(T,C,Q,E)

(5)

若偏好关系>，～，<满足

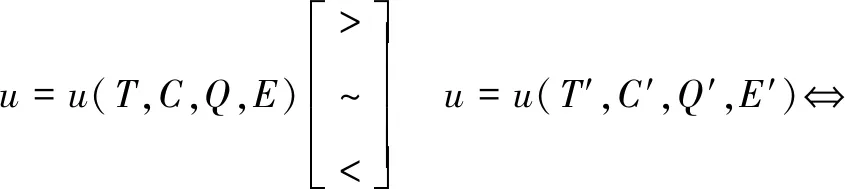
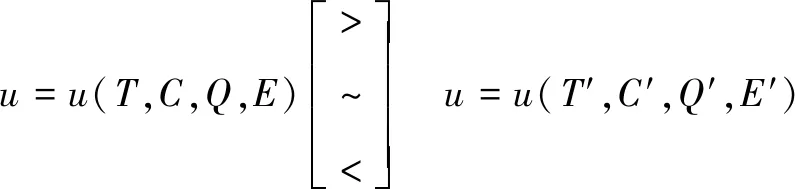
(6)

则将函数u=u(T,C,Q,E)称为多属性效用函数。由多属性效用函数分解定理，可得

u(T,C,Q,E)=kTu(T)+kCu(C)+kQu(Q)+kEu(E)

(7)

kT,kC,kQ,kE≥0

(8)

kT+kC+kQ+kE=1

(9)

式中：u(T)、u(C)、u(Q)、u(E)分别为工期T、费用C、质量Q、绿色施工水平E的单变量效用函数；kT、kC、kQ、kE分别为各单变量效用函数的权重，各权重的取值一般由专家根据经验及偏好打分确定。

3.2 约束条件

约束条件是多目标优化模型的主要构成因素之一，多属性效用函数的约束条件由各单项工作在网络计划中的逻辑关系，即工期、质量、绿色施工水平、费用相互关系，以及各变量的域值确定。可得工期、费用、质量、绿色施工水平等四个指标的效用函数分别为

u(T)=a+b(T-Tmin)2

(10)

u(C)=c+d(C-Cmin)2

(11)

u(Q)=e+f(Q-Qmin)2

(12)

u(E)=g+h(E-Emin)2

(13)

式中：a、b、c、d、e、f、g、h可由工期T、费用C、质量Q、绿色施工水平E的上下限求得。

3.3 绿色施工多目标优化模型

考虑各指标的权重系数kT、kC、kQ、kE，将工期、质量、绿色施工水平、费用四个指标分别对应的效用模型，代入多属性效用模型中，可得水环境治理项目优化模型的目标函数为

(14)

s.t.

Tmin≤T≤Tmax

(15)

Cmin≤C≤Cmax

(16)

Qmin≤Q≤Qmax

(17)

Emin≤E≤Emax

(18)

4 绿色施工优化求解

遗传算法[11-12](Genetic Algorithm，GA)是一种借鉴基因遗传机理来模拟群体自然进化过程的随机搜索最优解的进化算法。遗传算法已被人们广泛应用于组合优化、机器学习、信号处理、自适应控制等领域。

遗传算法的基本原理是用某种编码表示问题的潜在解集，并产生初始种群，种群中的个数代表染色体的数量，通过不断淘汰劣质染色体，逐步使种群进化到包含近似最优解的状态[13]。

4.1 基本思路

在遗传算法优化求解的过程中，采用数字编码的方式，输入项目的质量、工期、费用、绿色施工水平等数据，染色体对应的基因位代表工序号，该项工序实际持续时间代表各染色体对应的基因值，初始种群个体的基因值通过随机方式在定义区间内产生。各工序的费用、质量、绿色施工水平可由式(1)、(3)、(4)计算得出。

4.2 适应度及遗传算子

适应度函数用来表征种群中每个个体对其生存环境的适应能力，直接决定着群体的进化行为。在遗传算法中适应度值规定为非负，并且在任何情况下总是希望越大越好[14]。遗传算子包括交叉和变异，pc为交叉概率，pm为变异概率，交叉概率介于0.6～1.0之间，变异概率介于0.001～0.1之间。变异过程可以看作是在项目持续时间内重新产生的一个随机值，适应度函数由目标函数u(T,C,Q,E)的最大值确定。

5 工程案例及应用分析

5.1 工程概况

徐州市奎河水环境综合整治工程，包括生态化改造现有老驳岸、河道清淤、绿化景观提升、调蓄池、沿河截污管网等项目，其中调蓄池为制约本项目的关键工程，因此选择调蓄池开展绿色施工多目标优化。调蓄池南北方向长79.4m，东西方向宽66.4m，基坑深7.7m(局部深9.5m)，包括支护、开挖、抗浮锚杆、底板、内部结构等工序。

5.2 绿色施工参数

对调蓄池施工工序进行分析，可得调蓄池施工进度网络，见图2。各工序内容见表1。项目的关键路径为：A→B→C→D→F→H→J→K→N→O。

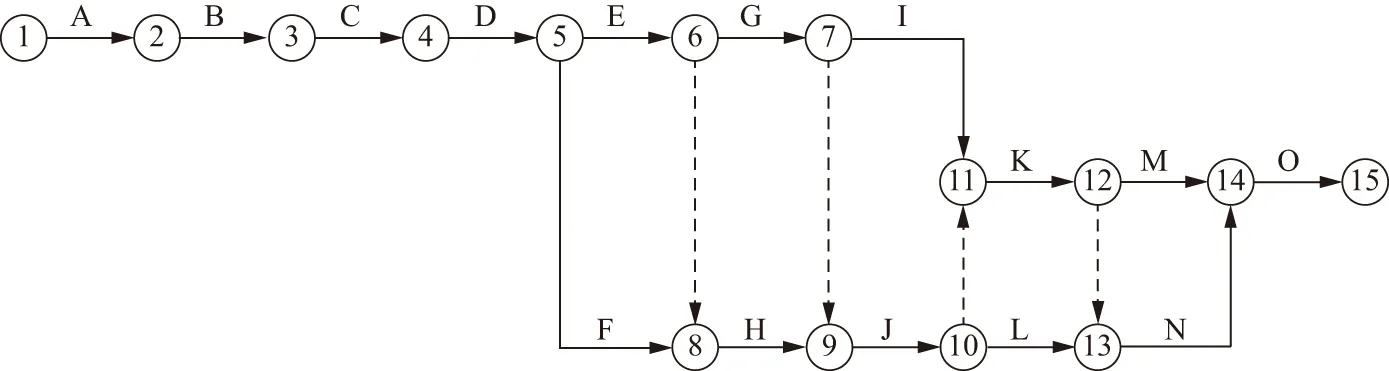
图2 施工进度网络

表1 各工序代号内容

邀请专家对各工序的施工参数进行评估，在分析项目资源投入、工程措施、材料使用等情况的基础上，采用层次分析法，同时结合相关规范标准以及专家个人经验，得到关于工期、费用、质量、绿色施工水平的相关参数，见表2～表3。根据表2和表3中的数据，结合工期分析，可得Tmax=381天，Tmin=326天，Cmax=3076万元，Cmin=2650万元，Qmax=100分，Qmin=87.6分，Emax=100分，Emin=86.4分。

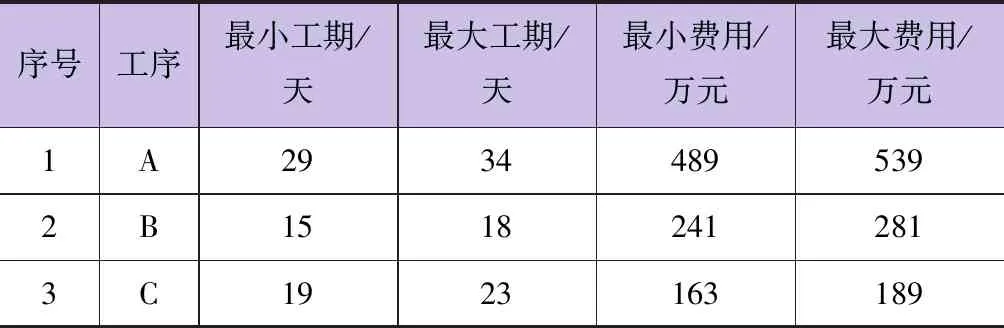
表2 各工序工期、费用参数

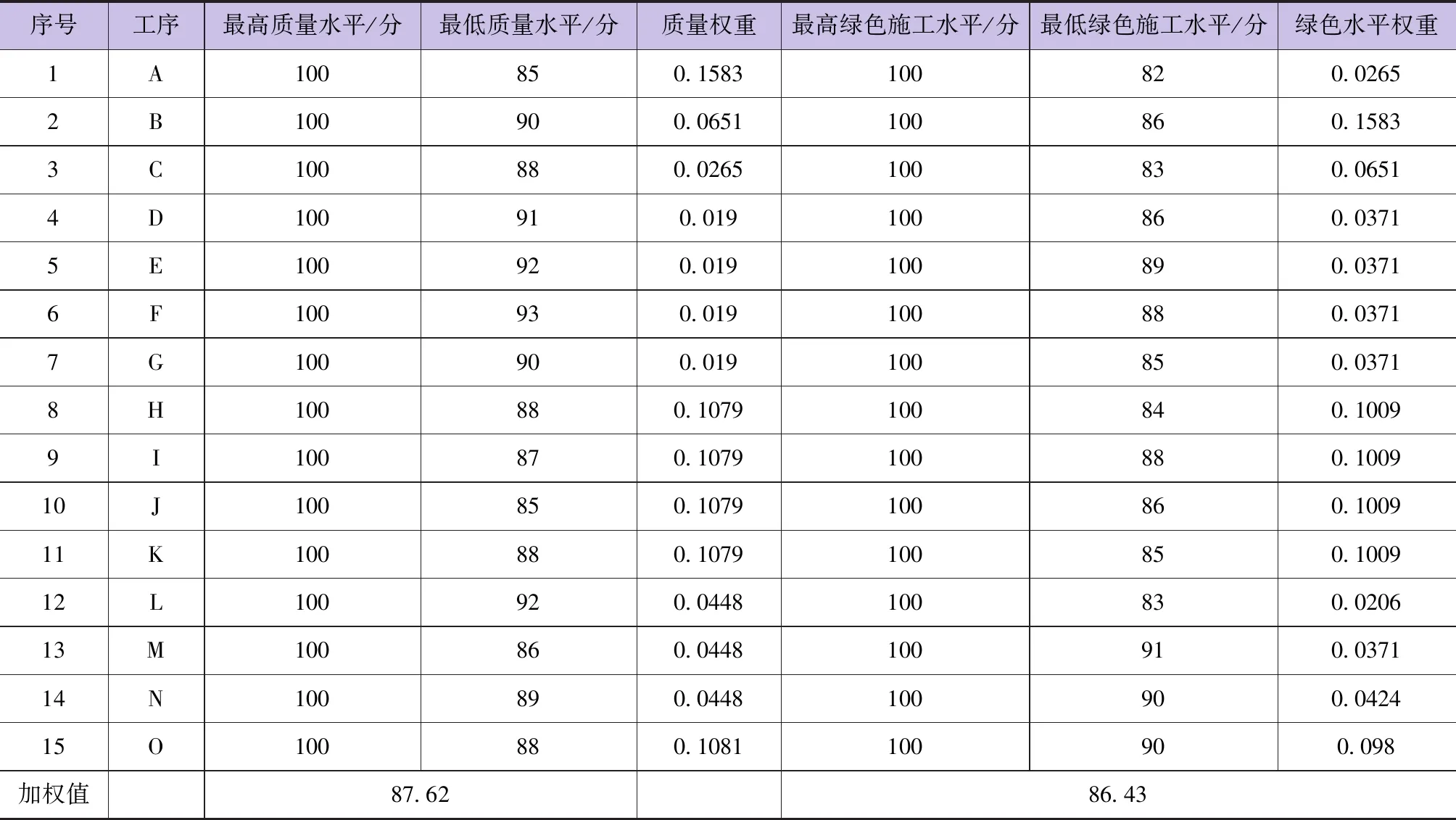
表3 各工序质量得分及绿色施工水平

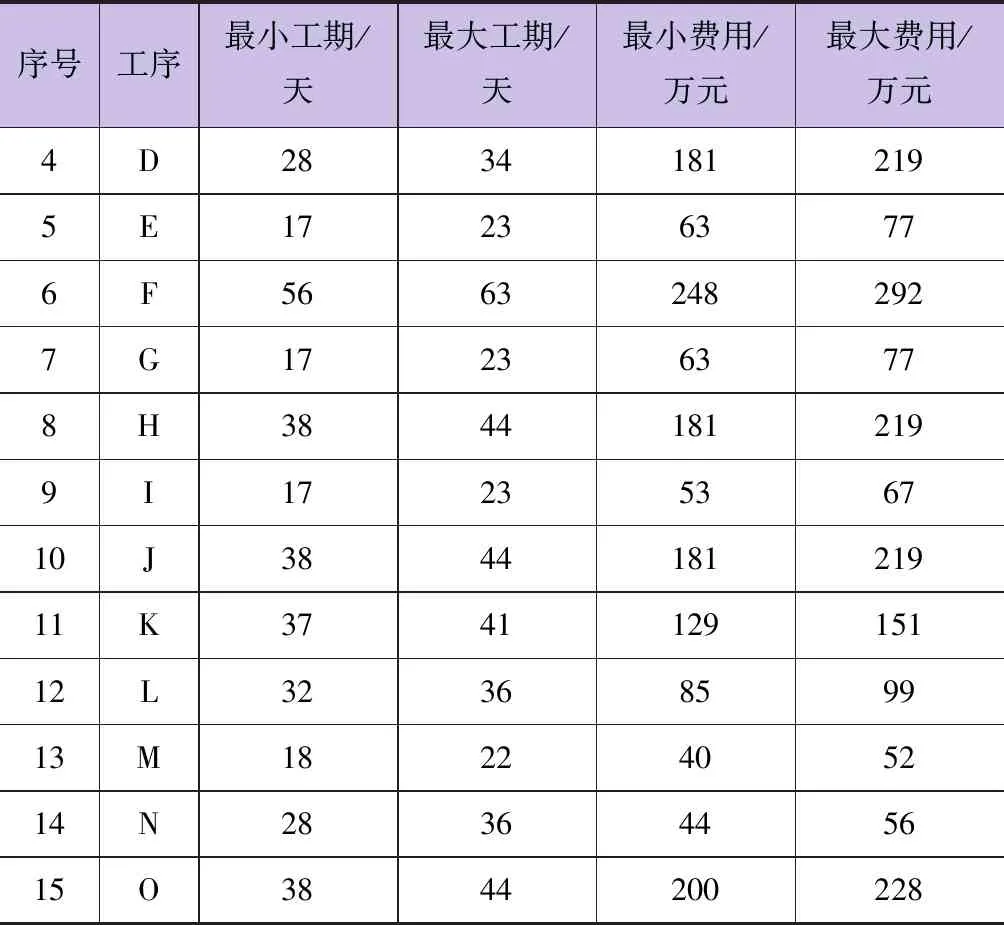
续表

5.3 绿色施工优化及分析

基于前述分析，将交叉概率pc设定为0.8，变异概率pm设定为0.05，遗传种群初始规模设为500，终止遗传运算的迭代次数设定为500，采用遗传算法计算，迭代结果见图3。由图3可知，在迭代次数达到80次左右时，计算结果开始收敛，最佳适应度与平均适应度趋于一致，此时的解为最优解，计算结果为(T,C,Q,E)=(347，2830，90.77，88.56)，u(T,C,Q,E)=0.9533。从优化结果可以看出，在满足工程质量、绿色施工要求的前提下，工程费用控制在了一个合理水平，工期控制在了一个较低值，项目综合效应达到了较高水平。

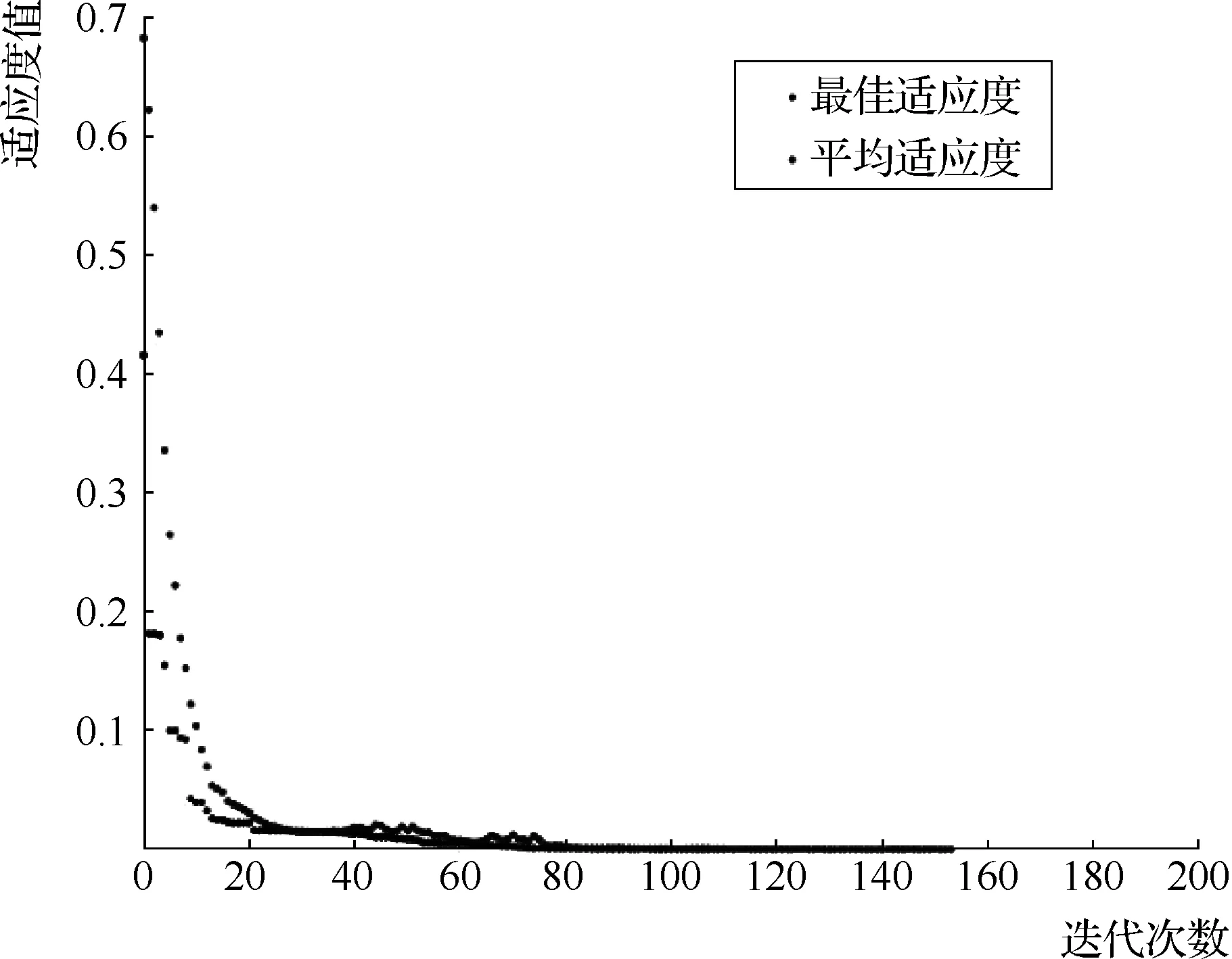
图3 计算迭代结果

优化结果表明，对于城市水环境治理项目，采用遗传算法可为项目决策提供有效依据，在满足绿色施工目标的前提下，实现工程效益的优化。

6 结 论

相较于传统项目的控制目标，本文引入绿色施工控制目标，将环保因素纳入绿色施工管理中。由于水环境治理项目涉及的影响因素较多，采用线型关系存在一定的不足，可以采用二次函数构建以质量、进度、费用、环保为控制因素的绿色施工多目标优化模型；为便于统一分析，可以采用多属性效用函数对分析指标进行归一化处理。工程应用表明，采用遗传算法对典型项目绿色施工多目标进行优化后，在满足绿色施工水平及工程质量的前提下，项目工期及费用都达到了相对较优的水平，该方法可以为项目决策提供有效依据。