融合深度特征的通道可靠性目标跟踪算法*
2022-04-12杨海清林小明
杨海清, 林小明
(浙江工业大学 信息工程学院,浙江 杭州 310023)
0 引 言
目标跟踪是计算机视觉的基本问题之一,具有许多实际应用的场景,例如视频监控,人机交互等。由于形变、光照变化、尺度变化和快速运动等复杂因素的存在,此问题仍具有挑战性。
近几年,基于相关滤波的方法在准确性和鲁棒性方面已显示出持续的性能改进。Bolme D S等人[1]提出最小输出均方误差(minimum output mean square error,MOMSE)跟踪器,该跟踪器与当时的主流跟踪器相比,在性能方面取得了极大的领先,同时,跟踪速度也达到了几百帧每秒。Henriques J F等人[2]在MOMSE的基础上引入了循环结构和核(cyclic structure and kernel,CSK)技巧来训练滤波器,因为仅使用单通道的灰度特征,对于快速运动和颜色变化的目标跟踪效果很差。Henriques J F等人[3]在CSK的基础上使用目标特征的循环移位和循环矩阵在傅里叶域中的对角化性质获得岭回归封闭解,极大提高了跟踪速度,但仅使用单一HOG特征,在一些复杂场景下,该跟踪效果仍然很差。Danelljan M等人[4]使用位置滤波器和尺度滤波器对目标进行位置和尺度估计。Li Y等人[5]利用多个特征的尺度采样来自适应的估计目标尺度。Danelljan M等人[6]在判别相关滤波器的基础上引入空间正则化来减轻边界效应,进一步提高跟踪的准确性。上述所提到的方法仅仅使用手工特征,不能很好地表征目标的外观模型。同时,上述方法对于每一帧均更新滤波器,当目标被遮挡时,容易使模板发生漂移。
本文利用深度特征[7](Conv5—4,Conv5—5)包含的语义信息结合手工特征的(HOG,CN,Gray)纹理信息的方式,分别训练相关滤波器,根据可靠性系数进行响应图自适应通道可靠性加权融合。同时通过判断主旁瓣比(PSR)和响应图的有效局部最大数量(NELM)是否满足给定的阈值,从而对模型进行自适应更新。
1 相关知识
一般性的相关滤波跟踪器在跟踪目标的过程中分为训练、检测和更新模型三个阶段。
训练阶段:在初始帧中,提取以目标位置为中心,大小为M×N的图像块来训练相关滤波器,并通过循环移位得到训练样本x(m,n)∈{0,1,…,M-1}×{0,1,…,N-1}。通过求解岭回归的最小封闭解问题得到最优滤波器w
(1)
式中λ为正则化参数,X为所有训练样本所组成的样本矩阵,y为训练样本X的期望输出。将式(1)转换到频域内求解得到第d(d∈{1,…,D})维通道的滤波器
(2)
式中 ⊙为元素点积,大写字母为傅里叶变换(例如:X=F(x)),X*为X的复共轭。
检测阶段:滤波器训练完成后,对于新读入的视频帧,在新的视频帧中截取以上一帧中目标位置为中心,大小为M×N的图像块Z来进行检测,响应图的计算公式为
(3)
响应图的最大值处即为新视频帧中目标所在位置。跟踪过程中,为了抑制边界的影响,采用汉明窗进行处理。
模型更新阶段:在目标跟踪过程中,目标的外观不可能保持一成不变,因此,为了能够跟踪上目标,对滤波器模板的分子和分母同时进行更新,更新方式为
(4)
式中θ为学习率,t为当前帧。
2 方 法
2.1 算法流程
图1为所提方法的整体流程。首先,提取输入图像的手工特征(HOG,CN,Gray),使用VGG—19网络进行深度特征提取,分别提取Conv4—4层和Conv5—4层的深度特征,独立训练每种通道特征的相关滤波器,得到对应通道特征的相关响应图。接着,计算每个通道可靠性系数H,通过自适应通道可靠性加权融合得到最终的响应图。最后,当目标被遮挡时,为了避免滤波器学习到背景信息,从而导致目标跟踪失败,只有NELM和PSR指标满足给定的阈值时,才能对模型进行更新。
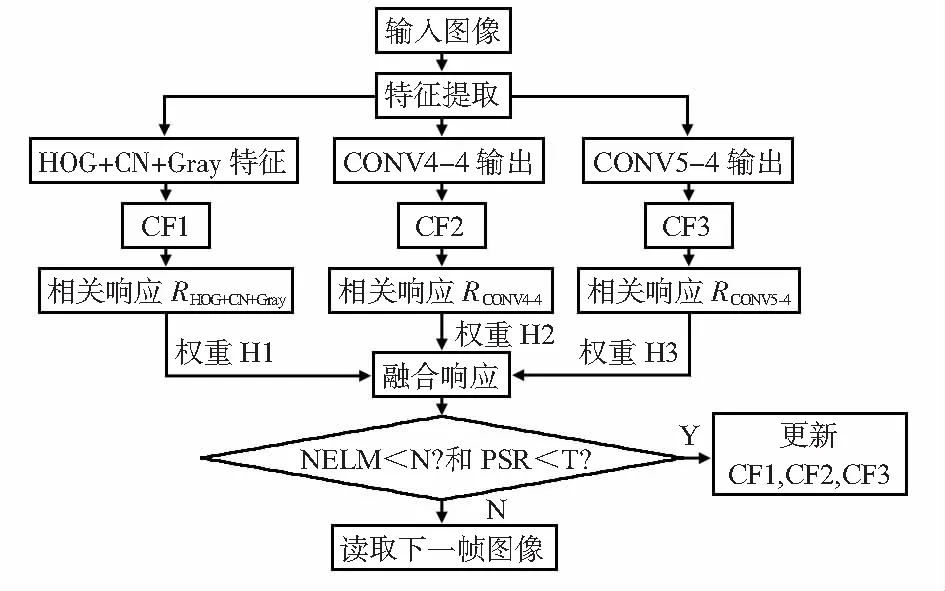
图1 算法流程框图
2.2 通道可靠性评估和自适应响应融合
通道可靠性反映了每一种通道特征在目标定位阶段中的重要性,它由通道学习可靠性和通道检测可靠性组成。通道可靠性的公式定义为
(5)

(6)
其中,Wd由式(2)计算得到,Xd为第d维通道特征。
(7)

在跟踪目标的过程中,目标的外观模型会发生变化,因此,需要对通道可靠性系数进行更新,公式为
Ht=(1-θ)Ht-1+θH
(8)
式中Ht-1为前一帧的通道可靠性,θ为学习率。
最后,进行自适应响应图融合,得到最终的响应图R。根据式(5)计算每个通道特征的可靠性加权因子
R=H1·RHOG+CN+Gray+H2·RCONV4-4+H3·RCONV5-4
(9)
其中,H1+H2+H3=1。
2.3 遮挡检测模型更新策略
在最小化输出均方误差[8]滤波器(MOSSE)中,PSR用于描述响应图的状态以检测跟踪是否失败,PSR被定义为
(10)
式中gmax为峰值,μ为旁瓣的平均值,σ为旁瓣的标准偏差。
然而,当目标快速移动或者处于低分辨率状态下时,PSR不能精确反映出目标是否被遮挡,因此,引入响应图有效局部最大数量(NELM)来进行遮挡检测。
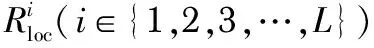
(11)
因为目标在两帧之间的运动应该是平稳的,因此,从视频序列的第二帧获得的响应图中,除(目标位置)以外的局部最大值被视为阈值β
β=max(Ti)
(12)
在后续帧的响应图中,Ti如果大于阈值β,则Ri被记录为有效局部最大值。NELM表示为
NELM=Crad{Ti|Ti>β}
(13)
式中 Crad为集合中元素的数量。如果有效局部最大响应值存在(如,NELM大于1,PSR小于给定的阈值τ。),则说明目标被遮挡,不更新模型。如果没有局部最大响应值存在(即NELM=0),不管PSR是高于给定的阈值还是低于给定的阈值,则按(4)式更新模型。
3 实验结果与分析
3.1 实验环境与参数设置
本次实验在Intel Core i5—8300CPU、主频2.30 GHz、运行内存8 GB的笔记本电脑上运行,使用的仿真软件为MATLAB2016a。本文算法参数设置:相关滤波学习率θ=0.01,正则化参数λ=10-4,阈值τ=7.0。
3.2 定量评估
为了验证本文所提算法的有效性,从0TB—100数据集上选取30个具有挑战性的视频序列进行验证,这些视频序列中包含目标跟踪中的常见挑战,包括光照变化、尺度变化、遮挡、快速运动、运动模糊、平面内旋转、平面外旋转等挑战因素。本次实验使用一次性评估方法(OPE)进行评估,评估指标为精度得分和成功率。精度ρ为所跟踪目标的实际中心位置与标准中心位置的欧氏距离
(14)
式中 (xc,yc)为目标的实际中心位置,(xg,yg)为目标的标准中心位置,精度分数(precision)定义为低于一个特定阈值ρ的视频帧数占视频总帧数的百分比。重叠率(IOU)表示在当前帧中,跟踪框和标准框的重叠面积与两个框的总面积的比值
(15)
式中BT为跟踪框,BG为标准框,成功率定义为重叠率超过一个特定阈值的视频帧数占视频总帧数的百分比。
所提算法与六种主流算法进行比较,包括HCFT[7],Staple[9],LMCF[10],KCF[3],DSST[4]、SAMF[5]。其中,HCFT仅使用深度特征,Staple使用的是颜色直方图和HOG特征,LMCF和SAMF使用的是HOG和CN特征,KCF和DSST使用的是HOG特征。本次实验主要评估了使用OPE方法的结果,在图2中,图(a)表示阈值在20像素处的距离精度得分,图(b)表示曲线下的面积。本文算法与六种主流算法相比,取得了最好的结果,精度达到了87.5 %,成功率则达到了77.8 %,分别高出第二名跟踪算法4.7 %和8.3 %,在所有比较的算法当中排名第一。
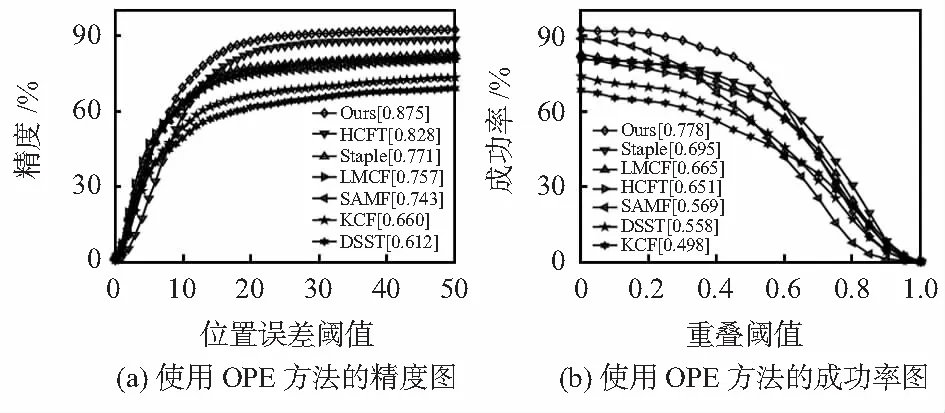
图2 距离精度和重叠成功率
3.3 定性评估
图3为所提方法与LMCF,Staple,HCFT,DSST跟踪算法在5个具有不同挑战因素的视频序列上进行的定性评估,分别是DragonBaby,MotorRolling,Human7,Pand和Jogging,从图3中可以得出,LMCF在目标被遮挡情况下能够继续跟踪到目标(Jogging),但当目标快速移动和发生旋转时(BragonBaby),其跟踪性能较差。Staple算法虽然对光照变化和尺度变化不敏感(Human7),但对快速运动、发生旋转的目标的跟踪性能也很差(MotorRolling)。HCHT算法虽然能够检测出目标所在的位置,但当目标的尺度发生变化或被遮挡时,不能自适应调整目标的尺寸和重新跟踪上目标。DSST算法可以对目标的尺寸进行预测,但当目标发生旋转或被遮挡时,会发生跟踪漂移。本文所提的算法能很好应对以上各种挑战因素,从5个测试序列可以看出,本文算法的跟踪性能均很好。

图3 五种跟踪算法的对比效果
4 结 论
在复杂场景下,针对使用单一特征的相关滤波器容易跟踪失败的问题,通过提取传统手工特征(HOG,CN,Gray)和深度特征来表征目标外观模型,实现了纹理信息和高语义信息的有效互补,进一步改善了目标的表征能力,同时,通过计算每个通道的可靠性系数,实现响应图的自适应通道可靠性加权融合,实现了目标的精确定位,在OTB—100上表明,所提算法能应对一些跟踪场景中的复杂变化(如目标旋转、快速移动、遮挡等),具有较高的跟踪精度和较好的鲁棒性。
