改进无迹粒子滤波的电动汽车锂电池SOC估算*
2022-04-12谭星浩刘有耀张雪兰
谭星浩, 刘有耀, 张雪兰
(西安邮电大学 电子工程学院,陕西 西安710121)
0 引 言
新能源汽车与传统燃油汽车最大的区别是用动力电池作为动力驱动[1],燃料电池电动汽车以其高效环保受汽车行业青睐,但燃料电池中氢气存储及安全性等问题使其商用需进一步研究,目前锂电池依然在新能源汽车中广泛使用。作为衔接电池组、整车系统和电机的重要纽带,电池管理系统(battery management system,BMS)的重要性不言而喻,对锂电池荷电状态(state of charge,SOC)的精准估算是动力电池延长使用寿命的重要参数[2]。
电动汽车动力电池SOC估测是BMS控制算法的核心所在,直接影响到电动汽车的续航能力和运行稳定性状态。锂电池SOC是非直接测量变量,不能通过传感器直接测量得到,只能通过可测量变量结合控制算法进行估算[3]。对SOC的估算常用的方法有:安时积分法、开路电压法、神经网络法和卡尔曼滤波法等[4]。安时积分法无法计算初始电量,并且会产生累积误差。开路电压法需要电池组静置较长时间,只适用于电动汽车停车检测,内阻法不适用于前期放电SOC估计。神经网络法需要大量参考数据进行训练计算量较大。卡尔曼滤波法对系统模型要求高,通常与其他算法结合[5]。
锂电池内部结构复杂,受内阻、温度、环境噪声等多个因素的影响[6],使得 SOC 精确计算比较困难。本文为了减小这些因素对锂电池SOC估算影响,采用改进无迹粒子滤波(improved unscented particle filtering,IUPF)算法,结合无迹卡尔曼滤波(unscented Kalman filtering,UKF )的粒子滤波算法可以有效避免外界环境等因素影响,使得对SOC估算精度更高。
1 电池模型的建立
对锂电池建模可以估计电池的开路电压,再根据开路电压(open circuit voltage,OCV)与SOC的对应关系可以估计当前电池的SOC值。因此选择一个合适的电池模型对电池SOC估算精度非常重要[7]。本文选用在Thevenin模型的基础上再增加一组RC回路组成的二阶RC模型,电路相对简单,误差较小,其等效电路如图1所示。
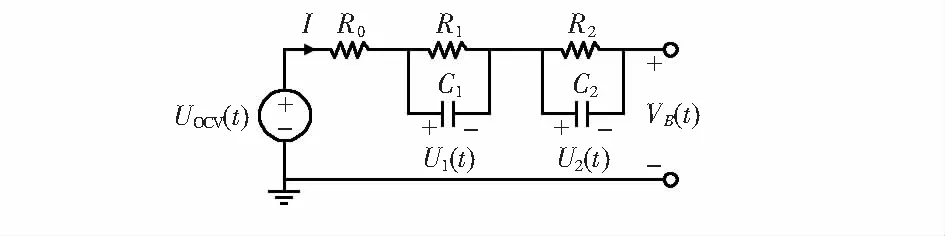
图1 锂电池等效电路模型
图1中UOCV(t)为开路电压,流过电池的电流用I表示;R0为电池欧姆内阻;R1,R2为电池极化内阻;C1,C2为电池极化电容。VB(t)表示电池模型的端电压,由KVL定律可得
VB(t)=VOCV(t)-U1(t)-U2(t)-IR0
(1)
电池SOC由安时积分法得
(2)
式中SOC0为SOC的初始值,QN为电池额定容量,η为库伦效率。
由戴维南定理可以得出以下数学关系式
(3)
VB(t)=VOCV(t)-I(t)R1(1-e-t/τ1)-
I(t)R2(I-e-t/τ2)-R0I(t)
(4)
(5)
VB,k=VOCV(SOCk)-U1,k-U2,k-Ik·R0
(6)
式中T为采样时间,wk为系统噪声。
2 电池模型参数辨识
等效电路模型中只有确定R0,R1,R2,C1,C2以及OCV-SOC特性曲线电池模型才会确定,系统采用Moli能源公司生产的18650型锰酸锂电池,其额定容量为30 Ah。本文通过恒流脉冲放电对电池参数进行辨识[8]。
实验过程在25 ℃环境温度1C放电倍率放电15 min,然后静40 min。实验得到的SOC和OCV值通过MATLAB中Cftool工具进行多项式拟合,发现5阶拟合效果良好,图2为SOC-OCV特征关系曲线。
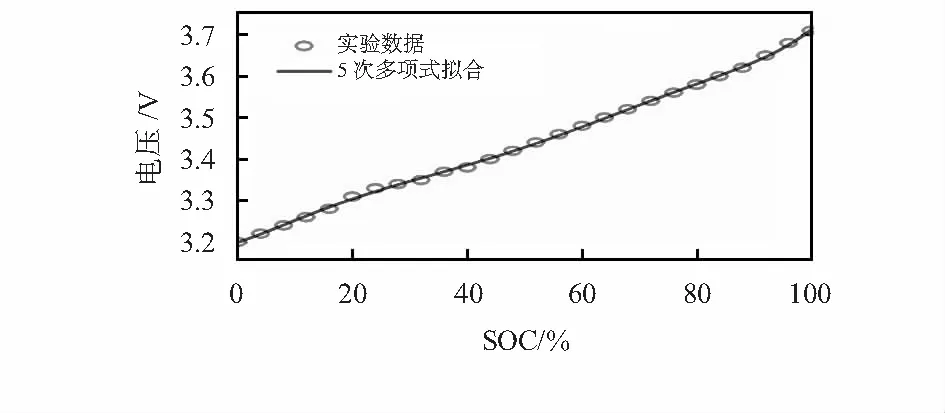
图2 SOC-OCV拟合关系曲线
SOC-OCV 关系的5阶多项式为
UOCV=-23.51×SOC5+18.69×SOC4-6.275×SOC3-
152×SOC2+1.28×SOC+2.24
(7)
对于模型内阻R0以及RC参数辨识需结合脉冲放电不同SOC点响应过程,图3是一次脉冲放电的电压响应示意图,A→B是静置状态,B→D是放电过程,E→F是放电结束后端电压零状态响应。根据图示变化过程可得
R0=UED/I
(8)
E→G间的电压可表示为
VB(t)-UOCV=k1e-λ1t+k2e-λ1t
(9)
结合式(4)可得
(10)
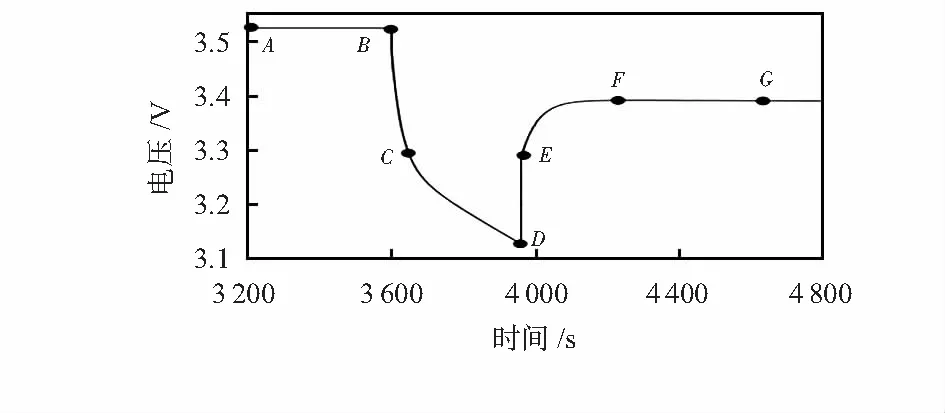
图3 一次完整脉冲放电过程
3 IUPF算法原理
粒子滤波(particle filtering,PF)是通过蒙特卡洛模拟的一种贝叶斯滤波方法[9],其核心思想是利用所求状态空间中大量样本的加权和表示后验概率密度,通过求和近似积分的操作[10]。传统粒子滤波需要大量的样本数量,由于没有考虑重样性函数的观测数据估计精度不高,本文结合UKF,通过选定的Sigma点来精确估计随机变量经过非线性变换后的均值和方差,从而更好地近似状态的概率密度函数[11]。
锂电池动态系统非线性离散模一般形式为
(11)
式中xk为k时刻的系统状态;uk为输入量放电电流;yk为输出量电池端电压;wk为随机噪声;vk为传感器噪声。
使用IUPF算法进行状态估计步骤如下:
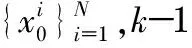
计算各采样点权系数
(12)
式中λ=α2(L+κ)-L,L为系统状态向量维数,α为比例缩放因子,决定了Sigma点分布状态,β用来描述偏离信息,λ为Sigma点的尺度参数,κ为副尺度参数[12]。
2)利用UKF更新粒子和UT变化建立Sigma点
(13)
建立Sigma点对观测噪声具有较强鲁棒性,式中Px为x的协方差。
时间更新
(14)
测量更新
(15)
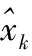
K=Pxy,k(Pyy,k)-1
(16)
3)计算SOC粒子重样性权值
(17)
4)粒子权值归一化
(18)
5)重采样:为了得到最优状态估计,通常使得粒子权值方差趋于零。有效粒子数Neff可表示为
(19)
为了减轻粒子退化,利用正则化粒子滤波来提高粒子集的多样性,首先用密度估计理论计算后验密度的连续分布,然后从连续分布中采样生成采样粒子,即
(20)

δ=(Nthr-Neff)/Nthr
(21)
式中Nthr为有效粒子数值,通过验证取Nthr=0.6N,如果Neff 按粒子权重排序 (22) 权重除以估计值与实际值的偏差 (23) 6)k时刻的状态最优估计值 (24) 7)k=k+1,得到新的观测值,返回步骤(2),直至循环结束,算法流程如图4所示。 图4 IUPF算法流程图 本文以额定电压3.7 V的三元锂电池为实验对象,实验平台由电池测试仪和计算机组成,各算法过程噪声矩阵Q=[10-9,10-9,10-10,10-8],观测噪声矩阵R=0.001,放电阶段的初始状态为x0=[0,0,0.065,0.87]T,PF算法和IUPF算法用于跟踪和预测的粒子数均为80,有效粒子阈值为0.6 N,初始协方差矩阵P0=[10-2,10-2,10-2,10-2]T,分别在恒流放电和动态应力测试(dynamic stress test,DST)下验证该算法的精度。 首先在1C恒流放电状态下对实验采集的数据进行模型验证,然后根据模型的辨识参数,分别为采用PF算法、UKF算法和IUPF算法进行SOC估算,并将估算结果与放电实验法获得的参考SOC值进行对比,IUPF估算下SOC初值为0.98,如图5所示,PF算法SOC估算误差最大,IUPF算法下 SOC估算更接近参考值。由恒流放电下SOC估算误差关系曲线可看出 PF算法有明显的初始误差。由于IUPF算法对重采样过程进行了优化,其估算结果误差较小。PF算法SOC估算最大误差为0.061 4,UKF算法下为0.038 7,IUPF算法下为0.018 6,由此可见IUPF算法对锂电池SOC估算精度明显优于PF与UKF算法。 图5 恒流放电下SOC估算及误差对比 电动汽车消耗锂电池基本在行驶过程中,电池在DSTSOC估算情况要比恒流条件下复杂,通过模拟工况放电来估算电池SOC对电动汽车续航以及电池健康状态非常重要。 由于PF算法误差较大,因此DST下未采用PF算法估算SOC,图6为DST下UKF算法、IUPF算法估算SOC与放电实验法测得SOC参考值及其误差对比,由图可知UKF算法SOC估算结果波动较大,而IUPF算法SOC估算比较稳定,基本与参考值一致。DST下两种算法SOC估算的误差值,UKF初始误差较大,而且变化幅度较大,DST下UKF算法SOC估算最大误差为0.148,IUPF算法抗干扰能力显著,IUPF算法最大误差为0.015 6,进一步提高了电池SOC估算的精度。 图6 DST下SOC估算及误差对比 本文主要研究IUPF算法来提高电动汽车锂电池SOC估算精度,通过建立二阶RC等效电路模型完成电池参数辨识,对实验获取的SOC和OCV数据进行五阶多项式非线性拟合。考虑到等效电池模型为非线性非高斯系统,利用UKF在粒子更新阶段调节Sigma采样点中比例缩放因子,提高了UT变换精度,为进一步提高电动汽车锂电池SOC估算精度,选用正则粒子滤波解决了粒子退化问题并筛选出优质粒子。为验证该算法的有效性,在恒流放电和DST工况下采用PF算法、UKF算法以及IUPF算法对电池SOC进行估算,并与实验所用的放电实验法SOC参考值进行对比,估算误差维持在2 %以内,估算精度明显高于其余两种算法,满足电动汽车锂电池管理系统设计需求。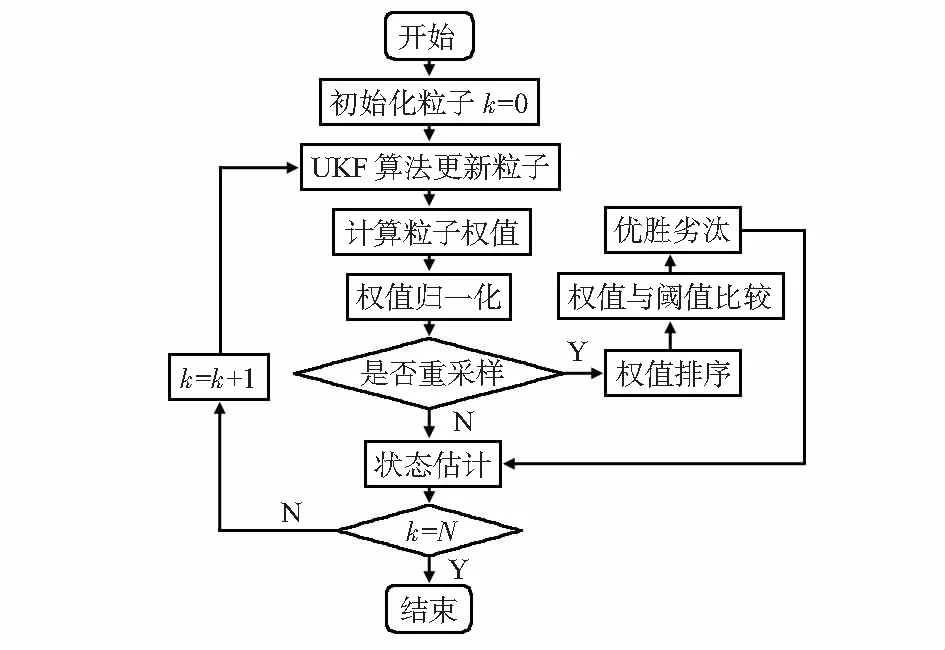
4 实验与仿真结果分析


5 结 论
