Research on Normal Pythagorean Neutrosophic Set Choquet Integral Operator and Its Application

Changxing Fan,Jihong Chen,Keli Hu,3,En Fan and Xiuqing Wang

1Department of Computer Science,Shaoxing University,Shaoxing,China

2College of Management Shenzhen University,Shenzhen,China

3Information Technology R&D Innovation Center of Peking University,Shaoxing,China

ABSTRACT We first propose the normal Pythagorean neutrosophic set(NPNS)in this paper,which synthesizes the distribution of the incompleteness,indeterminacy,and inconsistency of the Pythagorean neutrosophic set(PNS)and normal fuzzy number.We also define some properties of NPNS.For solving the decision-making problem of the nonstrictly independent and interacting attributes,two kinds of NPNS Choquet integral operators are proposed.First,the NPNS Choquet integral average(NPNSCIA)operator and the NPNS Choquet integral geometric(NPNSCIG)operator are proposed.Then,their calculating formulas are derived,their properties are discussed,and an approach for solving the interacting multi-attribute decision making based on the NPNS is studied.Finally,the two kinds of operators are applied to validate the stability of the new method.

KEYWORDS Normal pythagorean neutrosophic set (NPNS); NPNS choquet integral average (NPNSCIA)operator; NPNS choquet integral geometric (NPNSCIG)operator; multi-attribute decision making (MADM)

1 Introduction

As an important branch of modern decision theory, MADM is widely used in many fields such as economy, management, military, and engineering.One of the core problems of MADM is how to give the attribute values under each attribute.Since Zadeh [1] proposed the concept of fuzzy set (FS), FS has become a hot research topic.Different scholars apply various methods and new theories to fuzzy decision making, improve and optimize the existing problems in fuzzy decision making, and make its development more perfect and reasonable.To popularize the FS,in 1986, Atanassov [2] introduced the concept of intuitionistic fuzzy set (IFS)and studied it.IFS can express membership degree and non-membership degree at the same time, and their sum is less than or equal to 1.Compared with traditional fuzzy sets, IFS is more suitable for describing fuzziness and uncertainty in practical problems.However, in the process of dealing with decision making, the sum of membership degree and non-membership degree may be greater than 1.So Yager [3] proposed the Pythagorean fuzzy set (PFS), which allows the sum of membership degree and non-membership degree to be greater than 1, but its sum of squares is not more than 1.PFS is an extension of IFS.Therefore, the processing of fuzzy and uncertain information has a stronger performance.On the basis of Yager’s research, different scholars applied various methods and new theories to Pythagorean fuzzy decision making.For example, Peng et al.[4] put forward the Pythagoras soft set by integrating Pythagoras with the soft set.Liang and Peng et al.[5,6]studied interval-valued Pythagorean fuzzy sets.Liu et al.[7] proposed the Pythagorean hesitation fuzzy set by combining the Pythagorean and hesitation fuzzy set.Fan et al.[8] generalized the membership degree and non-membership degree of the Pythagorean fuzzy number and proposed the triangular Pythagorean fuzzy set.But IFS can only deal with incomplete information but not with uncertain and inconsistent information.Therefore, Smarandache [9,10] proposed the neutrosophic set (NS)theory based on IFS.It is a generalization of FS and IFS by adding independent uncertainty on the basis of IFS.In the NS theory, decision-makers can use the degree of truth, indeterminacy, and falsity to describe the evaluation of objective things.Since it was proposed, it has attracted extensive attention and research.Wang et al.[11] proposed a concept of single-valued neutrosophic sets (SVNS).Liu et al.[12] proposed a weighted aggregation operator and decision making method based on interval value neutrosophic sets (IVNS).Fan et al.[13-15]proposed decision making methods based on SVNS, linguistic neutrosophic multisets(LNM), and refined-SVNS.Liu et al.[16,17] proposed the normal neutrosophic set (NNS).Ye [18] proposed Correlation Coefficients of NNS.Jansi et al.[19] in 2019 proposed Pythagorean neutrosophic set(PNS)as an extension of Ajay et al.applied PNS in fuzzy graphs [20].

Ideally, the constructed decision indicator system should have the conditions of completeness,representativeness, and independence.However, in many practical cases, these attributes are usually not independent but correlated.In order to solve the MADM problem of attribute correlation,Marichal [21] in 2000 generalized the fuzzy measure defined by Sugeno [22] and proposed the Choquet integral [23].Since Choquet integral was put forward, it has been hotly discussed by many scholars.Xu [24] applied Choquet integral to multi-attribute decision making of intuitional fuzzy sets and proposed intuitional fuzzy correlated average operator, intuitional fuzzy correlated geometric operator, etc.Tan et al.[25] proposed intuitionistic fuzzy Choquet integral average operator and intuitionistic fuzzy Choquet integral geometric operator.Qu et al.[26] applied the Choquet integral to the interval-hesitation fuzzy multi-attribute decision making and proposed the interval-hesitation fuzzy Choquet integral operator.Peng et al.[27] applied Choquet integral to The Pythagorean fuzzy decision making environment and proposed the Pythagorean fuzzy Choquet integral average operator and geometric operator.Dong et al.[28] proposed Generalized Choquet Integral Operator of Triangular Atanassov’s Intuitionistic Fuzzy Numbers.Wan et al.[29] proposed Generalized Shapley Choquet integral operator based method for interactive interval-valued hesitant fuzzy uncertain linguistic.When solving MADM problems, Choquet integral operator can effectively deal with the redundant part of attribute compatibility, and solve the problem of attribute correlation by balancing the influence degree between attributes.In view of the Choquet integral operator can be used to consider the relationship between information, this paper proposes the normal Pythagorean neutrosophic set (NPNS)and generalize Choquet integral operator to the NPNS environment.NPNS synthesizes the distribution of the incompleteness,indeterminacy, and inconsistency of PNS and the normal neutrosophic number, which is more reasonable than PNS and NNS on expressing the decision making information.NPNS Choquet integral operator not only considers the importance between attributes but also reflects the relation between attributes.Then the properties of this operator are discussed, and an algorithm for solving the MADM problem is proposed based on this operator.

We organize the paper as follows.Section 2 describes basic concepts.Section 3 defines two Choquet integral operators of NPNS.Section 4 establishes the DM model based on NPNSCIA or NPNSCIG Operator.Section 5 provides an example.Section 6 gives conclusions.

2 Some Basic Concepts

2.1 Pythagorean Fuzzy set(PFS)

Definition 1[3].SetYas an object set, a PFS is expressed asΓ={y,(uΓ(y),vΓ(y))y∈Y},uΓ:Y ∈[0, 1] denotes membershipand νΓ:Y ∈[0, 1] denotes non-membership, and 0 ≤(uΓ(y))2+(νΓ(y))2≤1 for eachy∈Y.

2.2 Normal Fuzzy Number(NFN)

Definition 2[30].Setas the membership-function ofΓ, and thenΓ=(α,ε)is an NFN and all NFNs are denoted asN.

2.3 Neutrosophic Set(NS)

Definition 3[10,11].Set Y as an object set,thenis called neutrosophic set (NS),express truth-membership ,express indeterminacy-membership andexpress falsity-membership.and≥0.

2.4 Pythagorean Neutrosophic Set(PNS)

Definition 4[19].SetYas an object set,thenis called Pythagorean neutrosophic set (PNS),express truth-membership,express indeterminacy-membership andexpress falsity-membership.Hereandare dependent andis independent.∀y∈Y,and

2.5 Normal Pythagorean Neutrosophic Set(NPNS)

Definition 5.SetYis an object set,(α,ε)∈N, thenis defined as the normal Pythagorean neutrosophic set (NPNS)inexpress the truthmembership,express indeterminacy-membership andexpress falsity-membership.Hereare dependent andis independent.[0,1]and

For convenience, a normal Pythagorean neutrosophic element (NPNE)is denoted as=〈(α,ε),(J,K,L)〉.

Definition 6.Set=〈(α1,ε1),(J1,K1,L1)〉and=〈(α2,ε2),(J2,K2,L2)〉as two NPNEs, then we define the NPNEs’operations:

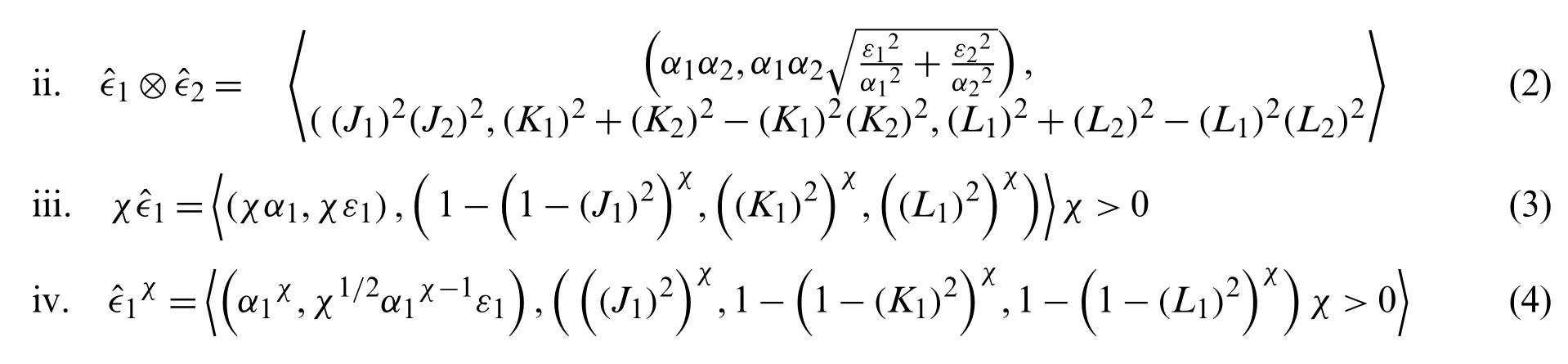
Definition 7.Set=〈(α,ε),(J,K,L)〉as a NPNE, and then its score functions are

and its accuracy functions are

Definition 8.Setas two NPNEs, then we have

2.6 Fuzzy Measure(FM)

Definition 9[22].SetD(Y)as the power set toY={y1,y2,...,yn},η(yi)expresses the weight ofyi, and thenη:D(Y)∈[0,1] is called theFMofYwhile satisfying the following conditions:

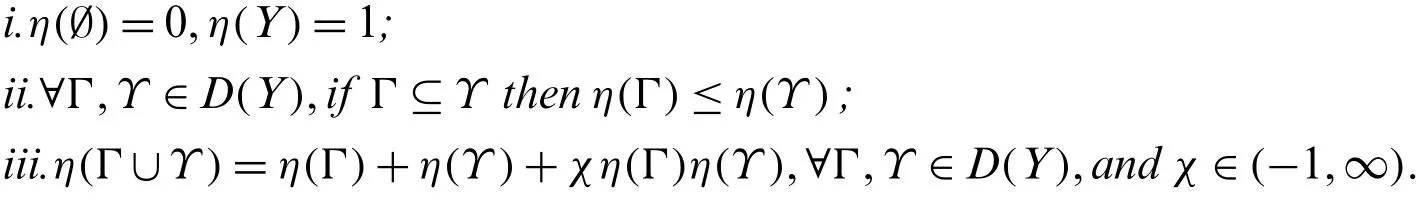
Ifχ= 0 thenη(Γ∪Υ)=η(Γ)+η(Υ), which indicates that the attribute setsΓandΥare independent of each other; if −1< χ <0 thenη(Γ∪Υ)< η(Γ)+η(Υ), which indicates that there is information redundancy between attribute setsΓandΥ; ifχ >0 thenη(Γ∪Υ)> η(Γ)+η(Υ), which indicates that there is information complementarity between attribute setsΓandΥ.

Forη(Y)=1, according to Eq.(9), whenϑ≠0,ηcan be confirmed:

2.7 Choquet Integral(CI)

Definition 10[21].SetY={y1,y2,...,yn}andηas an FM on Y andξas a nonnegative real value function.Then we define the Choquet integral of functionξaboutη:

In which(γ(1),γ(2),...,γ(n))express an arrangement and can makeξγ(1)≥ξγ(2)≥...≥ξγ(n)and,yγ(ς)expresses the corresponding weight toξγ(ς).

3 Two Choquet Integral Operators of NPNS

In this section, we define two normal Pythagorean neutrosophic set based Choquet integral operators, one is the normal Pythagorean neutrosophic set Choquet integral averaging (NPNSCIA)operator, and the other is the normal Pythagorean neutrosophic set Choquet integral geometric (NPNSCIG)operator.Meantime, we discuss some properties of them.

3.1 The NPNSCIA Operator

Definition 11.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), while

NPNSCIA is called the NPNS Choquet integral averaging operator, in which(γ(1),γ(2),...,γ(n))express an arrangement and can makeandZγ(■)=is the corresponding weight of

According to some relevant operation rules of NPNE, we can get the form of the NPNSCIA operator shown in Theorem 1.

Theorem 1.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), after using the NPNSCIA operator, the collective value obtained is also an NPNE and is denoted by

In which(γ(1),γ(2),...,γ(n))express an arrangement and can makeandand yγ(ς)is the corresponding weight of

Now, we proof Eq.(13).

Proof:

When n=1, we can easily get Eq.(13).

When n=2, we get:

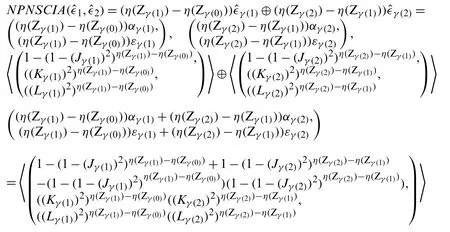
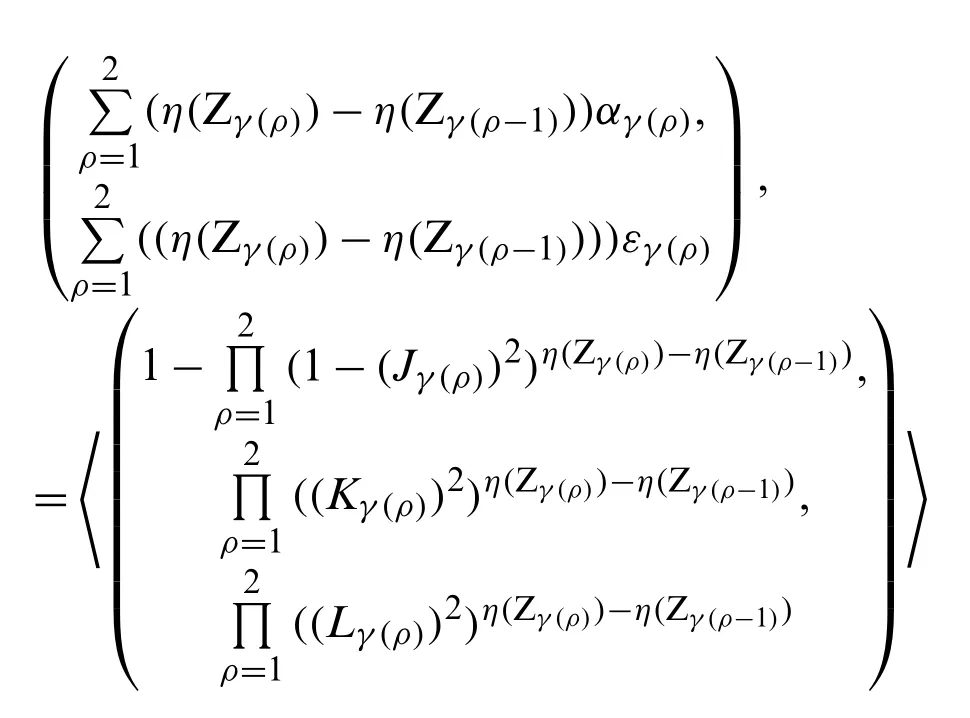
Making a hypothesis, whenn=ςthe Eq.(13)is established:

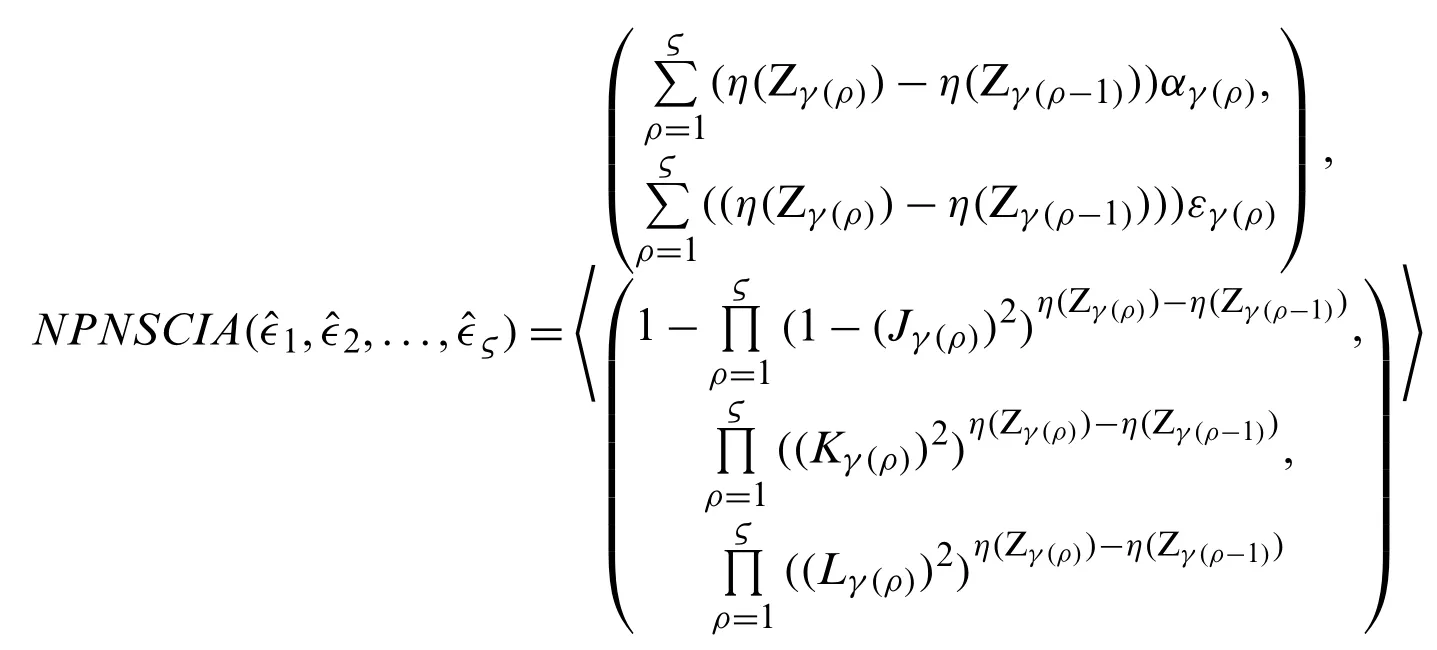
Thenn=ς +1,

This proves Theorem 1.

Theorem 2.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), ifthen

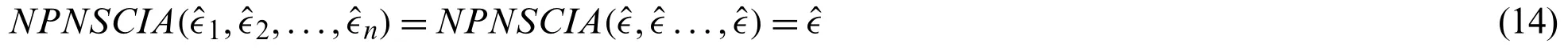
Proof:

NPNSCIA

Theorem 3.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), ifis a replacement ofthen

It is easy to prove it according to Definition 11, here we omit.

Theorem 4.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉and=〈(αρ∗,ερ∗),(Jρ∗,Kρ∗,Lρ∗)〉(ρ=1,2,...,n)as two collections of NPNE on Y, and their ranking orders arefor allρ, which meansαγ(ρ)≤αγ(ρ)∗,εγ(ρ)≥εγ(ρ)∗,(Jγ(ρ))2≤((Jγ(ρ))2)∗,(Kγ(ρ))2≥((Kγ(ρ))2)∗and(Lγ(ρ))2≥((Lγ(ρ))2)∗, then

Proof:

Sinceαγ(ρ)≤αγ(ρ)∗,εγ(ρ)≥εγ(ρ)∗for allρandη(Zγ(ρ))−η(Zγ(ρ−1))≥0 (can be got in Definition 10), then

Since(Jγ(ρ))2≤((Jγ(ρ))2)∗,(Kγ(ρ))2≥((Kγ(ρ))2)∗and(Lγ(ρ))2≥((Lγ(ρ))2)∗for allρthen

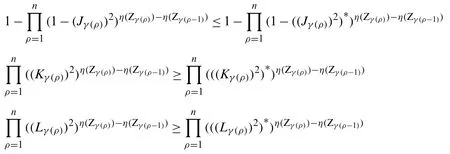
Theorem 4 has been proved.

Theorem 5.(Boundedness).Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), let=〈(min(αρ),max(ερ)),(min(Jρ2),max(Kρ2),max(Lρ2))〉 and=〈(max(αρ),min(ερ)),(max(Jρ2),min(Kρ2),min(Lρ2))〉, then

Proof:

To Theorem 2,

To Theorems 3-4,

3.2 NPNSCIG Operator

Definition 12.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), while

NPNSCIG is called the NPNS Choquet integral geometric operator, in which(γ(1),γ(2),...,γ(n))express an arrangement and can makeandand yγ(ς)is the corresponding weight of

According to some relevant operation rules of NPNSs, we can get the form of the NPNSCIG operator shown in Theorem 6.

Theorem 6.Setηas a fuzzy measure onY= {y1,y2,...,yn}, a collection of NPNE=(αρ,ερ),(Jρ,Kρ,Lρ)(ρ=1,2,...,n), after using the NPNSCIG operator, the collective value obtained is also an NPNE, denoted by

Theorem 7.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), ifthen

Theorem 8.Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), ifis a replacement ofthen

Theorem 9.Setηas a fuzzy measure onY={y1,y2,...,yn},=〈(αρ,ερ),(Jρ,Kρ,Lρ)〉and= 〈(αρ∗,ερ∗),(Jρ∗,Kρ∗,Lρ∗)〉(ρ=1,2,...,n)as two collections of NPNE onY, and their ranking orders areandfor allρ, that isαγ(ρ)≤αγ(ρ)∗,εγ(ρ)≥εγ(ρ)∗,(Jγ(ρ))2≤((Jγ(ρ))2)∗,(Kγ(ρ))2≥((Kγ(ρ))2)∗and(Lγ(ρ))2≥((Lγ(ρ))2)∗, then

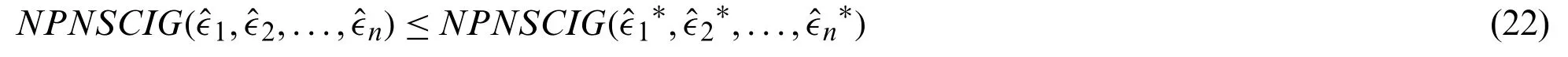
Theorem 10.(Boundedness).Setηas a fuzzy measure onY={y1,y2,...,yn}, a collection of NPNE= 〈(αρ,ερ),(Jρ,Kρ,Lρ)〉(ρ=1,2,...,n), let= 〈(min(αρ),max(ερ)),(min(Jρ2)max(Kρ2),max(Lρ2))〉and=〈(max(αρ),min(ερ)),(max(Jρ2),min(Kρ2),min(Lρ2))〉then

It is easy to prove Theorems 6-10.

4 Decision Making Methods Based on NPNSCIA or NPNSCIG Operator

The multi-attribute decision problem with decision information of NPNS is described as follows:There are m schemesH={h1,h2,...,hm} and n attributesT={t1,t2,...,tn}.The decision maker measures the schemeshiby attributetjand gets the valueof attributes, in whichhij=〈(αij,εij),(Jij,Kij,Lij)〉is an NPNE.Then, we can get the NPNE decision matrixC=(hij)mn.

Considering the correlation between attributes, by using the NPNS Choquet integral operator, a MADM method is presented in the NPNS environment.

Step 1:Build upC=(hij)mn;

Step 2:Calculate the fuzzy measure of attribute sets;

Step 3:Calculate by using the NPNSCIA or NPNSCIG operator;

Step 4:Calculate each scheme’s score value;

Step 5:Choose the best scheme.

5 An Illustrative Example

The company plans to choose one of the four suppliersH={h1,h2,h3,h4}with the strongest comprehensive ability as its long-term supplier,h1expresses the supplier A,h2expresses the supplier B,h3expresses the supplier C andh4expresses the supplier D.When making decisions,the company considers four attributesT={t1,t2,t3,t4}of suppliers:quality, production capacity,after-sales service and management ability, and their fuzzy measures areη1=0.3,η2= 0.3,η3=0.3and η4=0.2.

Step 1:In Table 1, the decision makers give the evaluation values described by NPNE.

Table 1:Matrix C

Step 2:Using Eq.(10), we calculateϑ=−0.2317;

Step 3:Using Eq.(9)andϑ, we get the fuzzy measure:

η(x1,x2)=η(x1,x3)=η(x2,x3)=0.5791;

η(x1,x4)=η(x2,x4)=η(x3,x4)=0.4861;

η(x1,x2,x3)=0.8389;η(x1,x2,x4)=η(x1,x3,x4)=η(x2,x3,x4)=0.7523;

η(x1,x2,x3,x4)=1.

Step 4:Using the NPNSCIA operator, we calculate each supplier’s comprehensive value.

h1=〈(5.1185,0.4719),(0.5363,0.1752,0.3892)〉;

h2=〈(6.1232,0.4626),(0.5323,0.1466,0.3600)〉;

h3=〈(4.7609,0.3677),(0.4346,0.1663,0.4960)〉;

h4=〈(5.5694,0.5000),(0.5129,0.1622,0.2939)〉.

Step 5:Each supplier’s score value can be gotten by using Eqs.(5), (6);

Φ1(h1)=10.7778;Φ1(h2)=13.0562;Φ1(h3)=9.1181;Φ1(h4)=11.9763.

Φ2(h1)=0.9937;Φ2(h2)=0.9864;Φ2(h3)=0.7042;Φ2(h4)=1.0752.

Step 6:According to the valueΦ1(hi)and the Definition 8, we rank each supplierh2≻h4≻

h1≻h3and choose the excellent supplierh2.

While using NPNSCIG operator:

Step 1’-3’:Just as Steps 1-3;

Step 4’:Using the NPNSCIG operator, we calculate each supplier’s comprehensive value.

h1=〈(4.8535,0.4894),(0.4529,0.1916,0.4202)〉;

h2=〈(5.9026,0.4630),(0.4276,0.1562,0.4615)〉;

h3=〈(4.6323,0.3960),(0.3829,0.1745,0.5438)〉;

h4=〈(5.5115,0.5143),(0.3391,0.1967,0.3437)〉.

Step 5’:Each supplier’s score value can be gotten by using Eqs.(5), (6).

Φ1(h1)=9.6674;Φ1(h2)=11.4833;Φ1(h3)=8.4328;Φ1(h4)=10.7924

Φ2(h1)=0.9748;Φ2(h2)=0.9007;Φ2(h3)=0.7209;Φ2(h4)=1.0071.

Step 6’:According to the valueΦ1(hi)and Definition 8, we rank each supplierh2≻h4≻h1≻h3and choose the excellent supplierh2.

Compared with the literatures [16-19], NPNS Choquet integral operator can not only model the weight of attributes and attribute-set in MADM problem, measure the correlation, complementary correlation, and preference correlation between attributes, but also can fully consider the importance between attributes, so as to make the decision results more objective.

6 Conclusions

In this paper, NPNS and Choquet integral operators are combined to define the NPNSCIA operator and NPNSCIG operator, which can consider the incidence relation between indicators.It is proved that they have power equality, displacement invariance, ordered monotonicity,and boundedness.A nonlinear programming model is established and the FM of indicators and indicator sets is solved objectively.In the NPNS environment, by using the defined operators and the established model, the problem of related MADM with attribute weight information unknown or partially attribute weight information unknown is solved effectively.Finally, the case proves that this method is easy and reasonable.This study extended the Choquet integral to NPNS, making the Choquet integral better applied and developed in the related MADM problems.

Funding Statement:This research was funded by the National Natural Science Foundation of China, Grant No.61703280; Zhejiang Provincial Natural Science Foundation of China, Grant No.LY20F020011; Social Sciences and Humanities Youth Foundation of Ministry of Education, Grant No.21YJCZH039; Natural Science Foundation of Zhejiang Province, Grant No.TY22F025548; the Public Welfare Technology Research Project of Zhejiang Province, Grant No.GG22F015473 and Key scientific research project of Shaoxing University, Grant No.2020LG1004.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.