On Degenerate Array Type Polynomials
2022-04-12LanWuXueYanChenMuhammetCihatDagliandFengQi
Lan Wu,Xue-Yan Chen,Muhammet Cihat Da˘gli and Feng Qi
1Key Laboratory of Intelligent Manufacturing Technology,Inner Mongolia Minzu University,Tongliao,028000,Inner Mongolia,China
2Department of Mathematics,Akdeniz University,Antalya,07058,Turkey
3Institute of Mathematics,Henan Polytechnic University,Jiaozuo,454010,China
4School of Mathematical Sciences,Tiangong University,Tianjin,300387,China
Dedicated to retired Professor Ji-Shan Tian,former vice president of Henan University,China
ABSTRACT In the paper, with the help of the Fa´a di Bruno formula and an identity of the Bell polynomials of the second kind,the authors define degenerate λ-array type polynomials,establish two explicit formulas,and present several recurrence relations of degenerate λ-array type polynomials and numbers.
KEYWORDS Degenerate array polynomial; Stirling number of the second kind; generating function; explicit formula;recurrence relation
1 Introduction
In this paper, we use the following notation:
Z={0,±1,±2,...}, N={1,2,...}, N0={0,1,2,...}, N−={−1,−2,...}.
The Stirling numbers of the second kindS(n,m)forn≥m≥0 can be generated by

and can be computed as

See [[1], p.206] and the paper [2].
Theλ-array type polynomialsS(n,m;x;λ)were defined in [3] by the generating function

See also the papers [4,5].It is clear thatS(n,m;0;1)=S(n,m).In the paper [6], Simsek obtained and constructed several generating functions and many relations of generalized Stirling type numbers, the array type polynomials, and Eulerian type polynomials.In the paper [7], Bayad et al.deduced interesting and meaningful identities associated withλ-array type polynomials,λ-Stirling numbers of the second kind, and the Apostol-Bernoulli numbers, while they dealt withλ-array polynomials by applyingλ-delta operator.Readers interested to the Apostol-Bernoulli numbers and polynomials may consult to the papers [8-10] and closely related references therein.
In the paper [11], Carlitz introduced degenerate Bernoulli and Euler polynomialsBn(x;γ)andEn(x;γ)by

and

respectively.Forx=0, the quantitiesBn(0;γ)andEn(0;γ)are called as degenerate Bernoulli and Euler numbers.Since limγ→0(1+γ t)1/γ=et, Eqs.(3)and (4)reduce to the generating functions for classical Bernoulli and Euler polynomials, respectively.
We now define degenerateλ-array type polynomialsS(n,m;x;λ;γ)by

It is easy to see that

which is defined by (2).Whenx=0, we call the quantitiesS(n,m;0;λ;γ)degenerateλ-array type numbers.
In this paper, utilizing the Faá di Bruno formula and an identity of the Bell polynomials of the second kind, we establish several explicit formulas and recurrence relations of (degenerate)λ-array type numbers and polynomials.
Let us notice that the Faá di Bruno formula, which can be viewed as an extension of chain rule to higher derivatives, has been applied to establish explicit and closed-form formulas of many important numbers and polynomials in analytic and combinatorial number theory.For more details, please refer to, for example, the papers [12-18] and closely related references therein.
2 Some Identities of the Bell Polynomials of the Second Kind
The Bell polynomials of the second kindBn,k(x1,x2,...,xn−k+1)forn≥k≥0 can be defined by

See [[1], p.134].Forn∈N, the Faà di Bruno formula is described in [[1], p.139] in terms of the Bell polynomials of the second kindBn,k(x1,x2,...,xn−k+1)by
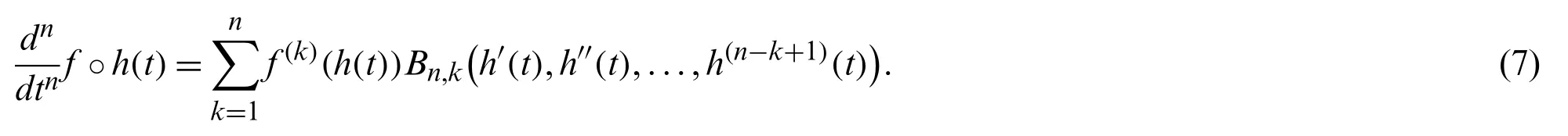
The formula
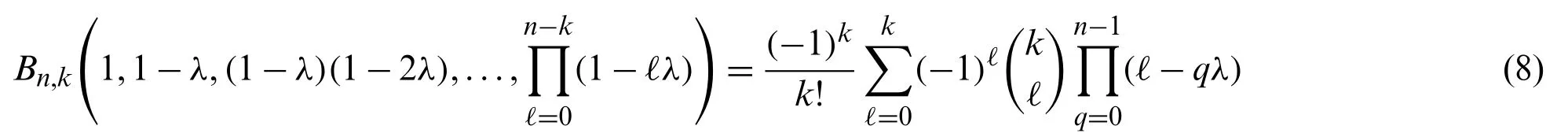
has been applied and reviewed in [[16], Lemma 2.2], [[17], Remark 6.1], and [[19], Section 1.3].
The explicit formula (8)is equivalent to

which was presented in [[20], Theorems 2.1 and 4.1], where the falling factorial 〈x〉nis defined forx∈C by

Whenn∈N, the explicit formulas (8)and (9)can be rearranged as
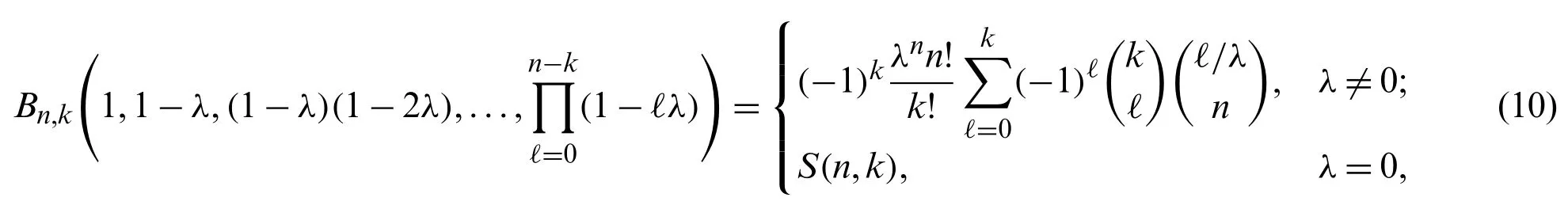
where extended binomial coefficientis defined by

and the classical Euler gamma functionΓ(z)can be defined by
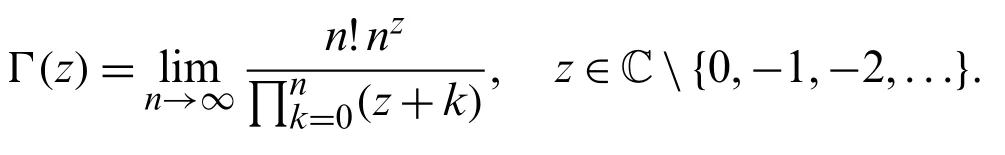
For new results and applications about the Bell polynomials‘of the second kindBn,k, please refer to the papers [13,19,21-23] and closely related references therein.
3 Explicit Formulas of Degenerate λ-Array Type Polynomials
In this section, we establish two explicit formulas for degenerateλ-array type numbers and polynomials, respectively.
Theorem 3.1.Forn∈N, degenerateλ-array type numbersS(n,m;0;λ;γ)can be computed by
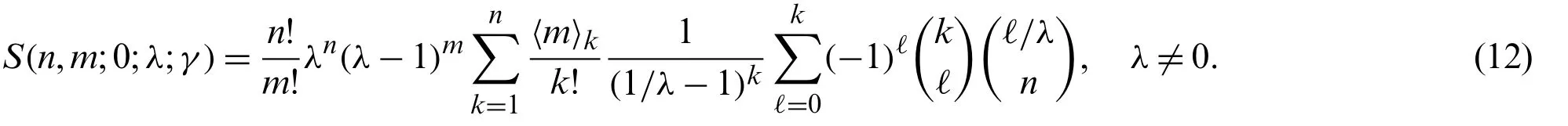
Proof.Making use off(u)=(λu−1)mandu=h(t)=(1+γ t)1/γ→1 ast→0 in the Faá di Bruno formula (6)and applying (10)result in


ast→0.Considering the generating function in (5)forx=0, we proved the explicit formula (12).The proof of Theorem 3.1 is complete.
Remark 3.1.From (5), it follows immediately that

By virtue of the explicit formula (12), we obtain the first few values of degenerateλ-array type numbersS(n,m;0;λ;γ)for 1 ≤n≤6 as follows:

Remark 3.2.The explicit formula (12)in Theorem 3.1 and seven concrete values listed in Remark 3.1 reveal that degenerateλ-array type numbersS(n,m;0;λ;γ)are polynomials ofλandγwith degreesmandn−1 ≥0, respectively.
Theorem 3.2.Forn∈N, degenerateλ-array type polynomialsS(n,m;x;λ;γ)can be computed by

Proof.Fork∈N, it is easy to see that

asu→1.Lettingu=h(t)=(1+γ t)1/γ→1 ast→0 and making use of the Faà di Bruno formula (7)give

ast→0.Considering the generating function in (5), we proved the explicit formula (13).The proof of Theorem 3.2 is complete.
Remark 3.3.From the generating function (5), we can easily obtain

By virtue of the explicit formula (13), we can calculate the first few values of degenerateλ-array type polynomialsS(n,m;x;λ;γ)for 1 ≤n≤3 as follows:

Remark 3.4.From the explicit formula (13)in Theorem 3.2 and the four concrete values in Remark 3.3, we conclude that degenerateλ-array type polynomialsS(n,m;x;λ;γ)are polynomials ofx,λ, andγof degreesn,m, andn−1 ≥0, respectively.
Remark 3.5.Whenx=0 in Theorem 3.2, the explicit formula (13)becomes (12)in Theorem 3.1.
Remark 3.6.For further better understanding degenerateλ-array type polynomialsS(n,m;x;λ;γ), we demonstrate two angles of the graph ofS(3,2;4;λ;γ)for −9< λ <9 and 0<γ <9 in Fig.1.The blue plane in Fig.1 is the(λ,γ)-plane.

Figure 1:Two angles of the graph of S(3,2;4;λ;γ) for −9<λ<9 and 0<γ <9, plotted by Wolfram Mathematica 12.0
Remark 3.7.For further better understanding degenerateλ-array type polynomialsS(n,m;x;λ;γ), we demonstrate two angles of the graph ofS(3,2;x;4;γ)for 0< x <9 and 0<γ <9 in Fig.2.The blue plane in Fig.2 is the(x,γ)-plane.

Figure 2:Two angles of the graph of S(3,2;x;4;γ) for 0 < x < 9 and 0 < γ < 9, plotted by Wolfram Mathematica 12.0
Remark 3.8.For further better understanding degenerateλ-array type polynomialsS(n,m;x;λ;γ), we demonstrate two angles of the graph ofS(3,2;x;λ;4)for 0< x <9 and−9<λ<9 in Fig.3.The blue plane in Fig.3 is the(x,λ)-plane.
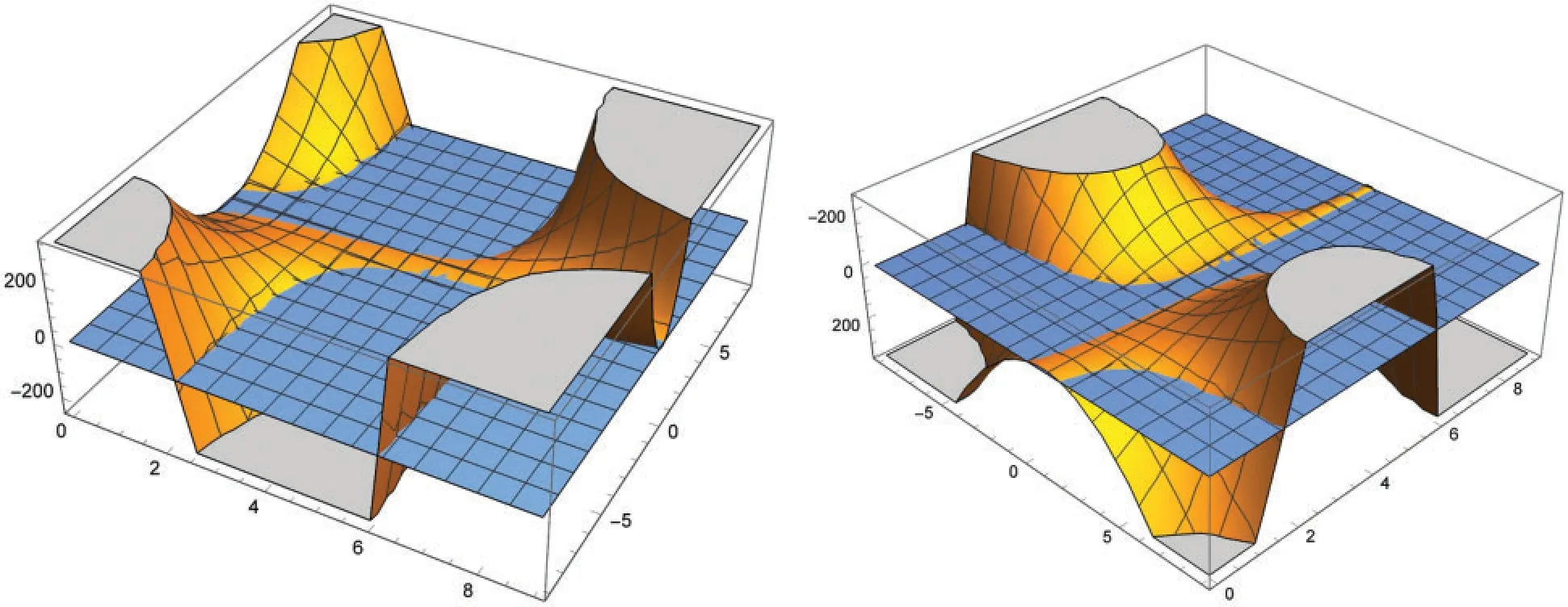
Figure 3:Two angles of the graph of S(3,2;x;λ;4) for 0 In this section, we establish several recurrence relations of degenerateλ-array type polynomials. Theorem 4.1.Degenerateλ-array type polynomials satisfy the recurrence relation Proof.From Eq.(5), it follows that Comparing coefficients of the termson both sides concludes (14).The proof of Theorem 4.1 is complete. Theorem 4.2.Degenerateλ-array type polynomialsS(n,m;x;λ;γ)satisfy the recurrence relation Proof.Differentiating with respect totyields where, on the other hand, and Further replacingxbyy+γand simplifying lead to (15). Takingγ→0 in (15)and considering (6)give (16).The proof of Theorem 4.2 is complete. Remark 4.1.One of anonymous referees commented that theλ-array type polynomials are related to numbers considered in the papers [24-26]. In this paper, with the help of the Faá di Bruno formula (7)and the identity (10)for the Bell polynomials of the second kindBn,k, we define degenerateλ-array type polynomialsS(n,m;x;λ;γ)by (5), establish two explicit formulas (12)and (13)in Theorems 3.1 and 3.2, and present several recurrence relations (14), (15), and (16)of degenerateλ-array type polynomials and numbersS(n,m;x;λ;γ)andS(n,m;λ;γ)in Theorems 4.1 and 4.2. Acknowledgement:The authors thank the editors and anonymous referees for their careful corrections to, valuable comments on, and helpful suggestions to the original version of this paper. Funding Statement:The first two authors, Mrs.Lan Wu and Xue-Yan Chen, were partially supported by the College Scientific Research Project of Inner Mongolia (Grant No.NJZY19156 and Grant No.NJZZ19144), by the Natural Science Foundation Project of Inner Mongolia (Grant No.2021LHMS05030), and by the Development Plan for Young Technological Talents in Colleges and Universities of Inner Mongolia (Grant No.NJYT22051)in China. Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.4 Recurrence Relations of Degenerate λ-Array Type Polynomials
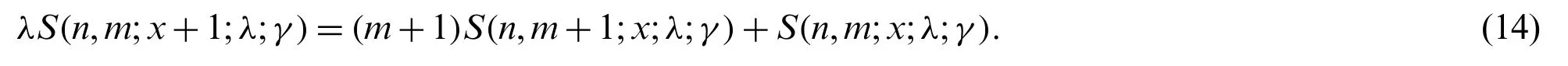




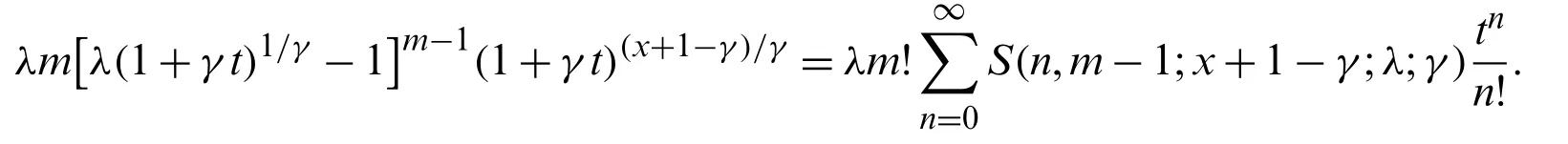
5 Conclusions
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- Noise Pollution Reduction through a Novel Optimization Procedure in Passive Control Methods
- Study of Effect of Boundary Conditions on Patient-Specific Aortic Hemodynamics
- Comparative Study on Deformation Prediction Models of Wuqiangxi Concrete Gravity Dam Based on Monitoring Data
- Mu-Net:Multi-Path Upsampling Convolution Network for Medical Image Segmentation
- An Approach for Quantifying the Influence of Seepage Dissolution on Seismic Performance of Concrete Dams
- Influence of Soil Heterogeneity on the Behavior of Frozen Soil Slope under Freeze-Thaw Cycles
