k-Order Fibonacci Polynomials on AES-Like Cryptology

Mustafa Asci and Suleyman Aydinyuz

Pamukkale University,Kinikli,Denizli,20160,Turkey

ABSTRACT The Advanced Encryption Standard(AES)is the most widely used symmetric cipher today.AES has an important place in cryptology.Finite field,also known as Galois Fields,are cornerstones for understanding any cryptography.This encryption method on AES is a method that uses polynomials on Galois fields.In this paper,we generalize the AES-like cryptology on 2×2 matrices.We redefine the elements of k-order Fibonacci polynomials sequences using a certain irreducible polynomial in our cryptology algorithm.So,this cryptology algorithm is called AES-like cryptology on the k-order Fibonacci polynomial matrix.

KEYWORDS Fibonacci numbers; Fibonacci polynomials; k-order Fibonacci polynomials; Fibonacci matrix; k-order Fibonacci polynomial matrix; Galois field

1 Introducti on

AES (Advanced Encryption Standard)is a standard offered for encryption of electronic data.AES, adopted by the American government, is also used as a defacto encryption standard in the international arena.It replaces DES (Data Encryption Standard).The encryption algorithm defined by AES is a symmetric-key algorithm in which the keys used in both encryption and decryption of encrypted text are related to each other.The encryption and decryption keys are the same for AES.

The algorithm standardized with AES was created by making some changes to the Rijndael algorithm, which was mainly developed by Vincent Rijmen and Joan Daeman.Rijndael is a name obtain using the developers’names:RIJmen and DAEmen.

AES is based on the design known as substitution-permutation.Its predecessor, DES, is an algorithm designed in Feistel structure.AES’software and hardware performance is high.The 128-bit input block has a key length of 128, 192 and 256 bits.Rijndael, on which AES is based,supports input block lengths that are multiples of 32 between 128 and 256 bits and key lengths longer than 128 bits.Therefore, in the standardization process, key and input block lengths were restricted.AES works on a 4×4 column-priority byte matrix called state.Operations in the matrix are also performed on a special finite field.

The algorithm consists of identical rounds that transform a certain number of repeating input open text into output ciphertext.Each cycle consists of four steps, except for the last cycle.These cycles are applied in reserve order to decode the encrypted text.The number of repetitions of cycles is a function of the key length according to Table 1.

Table 1:Key lengths and number of rounds for AES

These cycles include key addition, byte substitution, ShiftRow and MixColumn.We can see these cycles in Fig.1.One can see detailed information about AES in Fig.2 [1].

Figure 1:AES input/output parameters

Figure 2:AES encryption block diagram

A finite field, sometimes also called Galois field, is a set with a finite number of elements.Roughly speaking, a Galois field is a finite set of elements in which we can add, subtract, multiply and invert.Before we introduce the definition of a field, we first need the concept of a simple algebraic structure, a field.

1.1 Definition Field

A field F is a set of elements with the following properties:

• All elements of F form an additive group with the group operation “+” and the neutral element 0.

• All elements of F except 0 form a multiplicative group with the group operation “×” and the neutral element 1.

• When the two group operations are mixed, the distributivity law holds, i.e., for alla,b,c∈F:a(b+c)=(ab)+(ac).

Galois field arithmetic is the most widely used field involving matrix operations.One can see detailed information about the Galois field and the operations performed on it in [2].Also, you can find information on the classical cryptology benefit in [3].

In extension fieldsGF(2m)elements are not represented as integers but as polynomials with coefficients inGF(2).The polynomials have a maximum degree ofm−1, so that there aremcoefficients in total for every element.In the field, which is used in AES, each elementis thus represented as

A(x)=a7x7+...+a1x+a0,ai∈GF(2)={0,1}.

Note that there are exactly 256=28such polynomials.The set of these 256 polynomials is the finite fieldIt is also important to observe that every polynomial can simply be stored in digital form as an 8-bit vector

A=(a7,a6,a5,a4,a3,a2,a1,a0).

In particular, we do not have to store the factorsx7,x6, etc.It is clear from the bit positions to which powerxieach coefficient belongs.

Fibonacci numbers are defined by the recurrence relation ofFn=Fn−1+Fn−2forn≥2 with the initial conditionsF0=0 andF1=1.There are a lot of generalizations of Fibonacci numbers satisfied and studied by some authors.For more information one can see in [4-8].The Fibonacci Q-matrix is defined in [9,10] as follows:

andnthpower of the FibonacciQ−matrix is shown in [11-13] by

Fibonacci polynomials that belong to the large polynomial classes are defined by a recurrence relation similar to Fibonacci numbers.The Belgian mathematician Eugene Charles Catalan and the German mathematician E.Jacobsthal were studied Fibonacci polynomials in 1983.The polynomialsfn(x)studied by Catalan are defined by the recurrence relation

fn(x)=xfn−1(x)+fn−2(x)

wheref0(x)=0,f1(x)=1,f2(x)=xandn≥3.Fig.3 notice that forx=1,fn(1)=Fn,FnisnthFibonacci number.

Figure 3:The behavior of the first six Fibonacci polynomials

In [14], the k-order Fibonacci polynomial is defined by A.N.Philippou, C.Georghiou and G.Philippou in 1983.

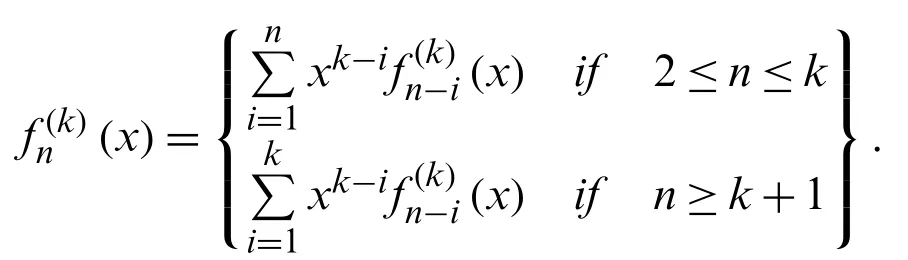
Kizilates et al.studied a new generalization of convolved(p,q)−Fibonacci and(p,q)−Lucas polynomials in [4].Also, Qi et al.gave a closed formula for the Horadam polynomials in terms of a tridiagonal determinant in 2019 in [15] and Kizilates et al.defined several determinantel expressions of generalized tribonacci polynomials and sequences in [5].In [6], Kizilates et al.introduced new families of three-variable polynomials coupled with well-known polynomials and numbers in 2019.New families of Horadam numbers associated with finite operators and their applications were studied by Kizilates in [7].

In [16], Basu et al.introduced the generalized relations among the code elements for Fibonacci coding theory in 2009.In 2014, Basu et al.defined a new coding theory for Tribonacci matrices in [17] and they expended the coding theory on Fibonacci n-step numbers in [18].Also, Basu et al.defined generalized Fibonacci n-step polynomials and stated a new coding theory called generalized Fibonacci n-step polynomials coding theory in [19].

In [19], fork≥2

whereF(k)n (x)is a k-order Fibonacci polynomials.

Diskaya et al.created a new encryption algorithm (known as AES-like)by using the AES algorithm in [20].They created the encryption algorithm by splitting the message text into 2×2 block matrices using Fibonacci polynomials.

Fibonacci polynomials have many applications in algebra.In recent years, we see that these polynomials have many uses in the field of engineering.Also, Fibonacci polynomials are used in solving differential equations.These solutions are used in engineering and science, adding new approaches to the solution of engineering problems.Mirzae and Hoseini solved singularly perturbed differential-difference equations arising in science and engineering with Fibonacci polynomials in [21].Also, in [22], Haq et al.studied approximate solution of two-dimensional Sobolev equation using a mixed Lucas and Fibonacci polynomials.

In this paper, we generalize the encryption algorithm given in [20] and study the encryption made with the 2×2 type block matrix operation to thek×ktype in Galois field.We redefine the elements of k-order Fibonacci polynomials sequences using a certain irreducible polynomial in our cryptology algorithm.The algorithm consist of four steps as in the AES encryption algorithm.The encryption algorithm defined in this algorithm is a symmetric-key algorithm in which the keys used in both encryption and decryption of encrypted text are related to each other.The encryption and decryption keys are the same like AES.So, this cryptology algorithm is called AES-like cryptology algorithm on the k-order Fibonacci polynomials.

2 The k-Order Fibonacci Polynomials Blocking Algorithm

In this chapter, we redefine the elements of k-order Fibonacci polynomial sequences using a certain irreducible polynomial in our coding algorithm.In extension fieldsGF(2m)elements are not represented as integers but as polynomials with coefficients inGF(2).Throughout this section, we takem=5 for next process.Sincem=5, we consider the finite Galois field containing 32 elements in this algorithm and this Galois field is denoted asNote that there are exactly 25=32 such polynomials.The set of these 32 polynomials is the finite fieldEach elements of this polynomials correspond to one letter of the alphabet.

The AES encryption algorithm uses theP(x)=x8+x4+x3+x+ 1 polynomial as the irreducible polynomial.

The irreducible polynomials ofare as follows:

x5+x2+1

x5+x3+1

x5+x3+x2+x+1

x5+x4+x3+x+1

x5+x4+x3+x2+1

x5+x4+x2+x+1.

In this paper, we consider the irreducible polynomials asP(x)=x5+x2+1.We can also diversify our encryption algorithm by using other irreducible polynomials.

Definition:In [8], the Fibonacci polynomial sequence {fn(x)}n≥0isf0(x)=0,f1(x)=1 andfn+2(x)=xfn+1(x)+fn(x).

For later use the first few terms of the sequence Fibonacci polynomials can be seen in the following Table 2 and a few the irreducible polynomials for Fibonacci polynomials are given as Table 3.

Table 2:Fibonacci polynomials

Table 3:Irreducible polynomials for Fibonacci polynomials

Polynomials of the Galois field are equivalent of each alphabet in Table 4 is as following:

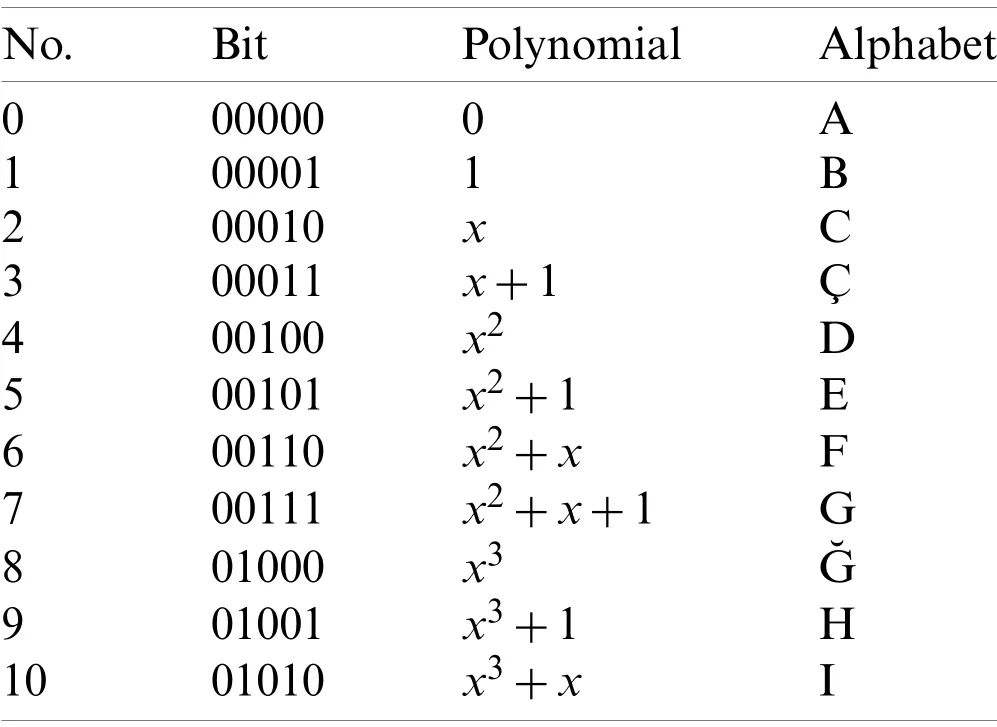
Table 4:Alphabet table

(Continued)

Table 4(continued)No.BitPolynomialAlphabet 1101011x3+x+1˙I 1201100x3+x2J 1301101x3+x2+1K 1401110x3+x2+xL 1501111x3+x2+x+1M 1610000x4N 1710001x4+1O 1810010x4+xÖ 1910011x4+x+1P 2010100x4+x2R 2110101x4+x2+1S 2210110x4+x2+x¸S 2310111x4+x2+x+1T 2411000x4+x3U 2511001x4+x3+1Ü 2611010x4+x3+xV 2711011x4+x3+x+1W 2811100x4+x3+x2X 2911101x4+x3+x2+1Y 3011110x4+x3+x2+xZ 3111111x4+x3+x2+x+1Q

Now, we obtain our encryption algorithm in line preliminary information we have given.

2.1 The k-Order Fibonacci Encryption Algorithm:The Coding Algorithm

• Step 1:We can consider the message text of lengthnand assume that each letter represents one length.

• Step 2:We can choose arbitrary value ofkandn.Thek-value we choose determine which order Fibonacci polynomials to use.We can create the matrixQnk(x)in Eq.(1)according to thekandnvalue we have chosen.Our message text is divided into blocks according to the valuek.We get matrices ofk×1 type.We get a new matrix by multiplying thek×1 type matrix with theQnk(x).Our new message is created by looking at the values in the matrix we obtained from the alphabet table.

• Step 3:We multiply the message matrix we just obtained by the invertible key matrix.In this paper, we accept the key matrix as follows:

1.KeyMatrix=

If there is an ascending 2 letters in the text, it letters is multiplied by 2.Key matrix in 2×2:

2.KeyMatrix=

• Step 4:The text created in the 3th step is collected sequentially with the k-order Fibonacci polynomials by starting from left and our encrypted message is created.

2.2 The k-Order Fibonacci Decryption Algorithm:The Decoding Algorithm

• Step 1:We can consider encrypted a text of lengthnand assume that each letter represents one length.

• Step 2:The text created is addition sequentially with the k-order Fibonacci polynomials by starting from the left and our new message is created.

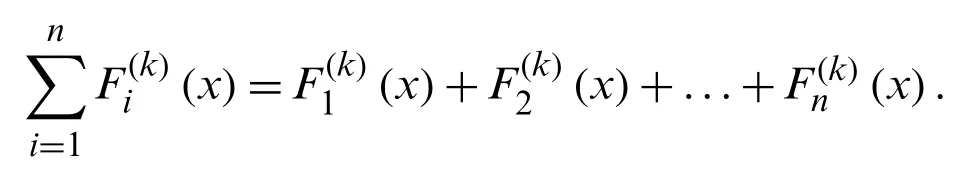
• Step 3:We multiply the message matrix we just obtained by inverse of the 1.key matrix.

InverseKeyMatrix=

If there is an ascending 2 letters in the text, it letters is multiplied by 2.Inverse key matrix in 2×2:

Inverse2.KeyMatrix=

• Step 4:We can obtain the matrixaccording to thekandnwe have chosen.Our text is divided into blocks according to the value k.We get matrices ofk×1 type.We get a new matrix by multiplying thek×1 type matrix with theOur new message is created by looking at the values in the matrix we obtained from the alphabet table.We can obtain our text message text.

2.3 Illustrative Examples for AES-Like Cryptology on the k-Order Fibonacci Polynomial Matrix

Example 1:Let us consider the message text for the following:

“HELLO”

Application to the Coding Algorithm:

• Step 1:“HELLO” is 5 letters.In this example, we encrypt process by choosingn=5 (We can choosenarbitrarily).

• Step 2:Fork=3 andn=5, we can use Tribonacci polynomials for encryption.

We can get as

It is known that

9=(01001)=x3+1=H

5=(00101)=x2+1=E

14=(01110)=x3+x2+x=L

17=(10001)=x4+1=O

So, it is

Since the word “HELLO” has 5 letters, we divide it into blocks of 3×1 and 2×1.So now we encrypt the 2×1 block with the usual Fibonacci polynomial matrix.

We can get in Eq.(1)as

So, it is

It results “HELLO”→“VVMKR”.

• Step 3:We multiply the message matrix we just obtained by the invertible 1.Key matrix.Turn into blocks of 3s and multiply with the key matrix.

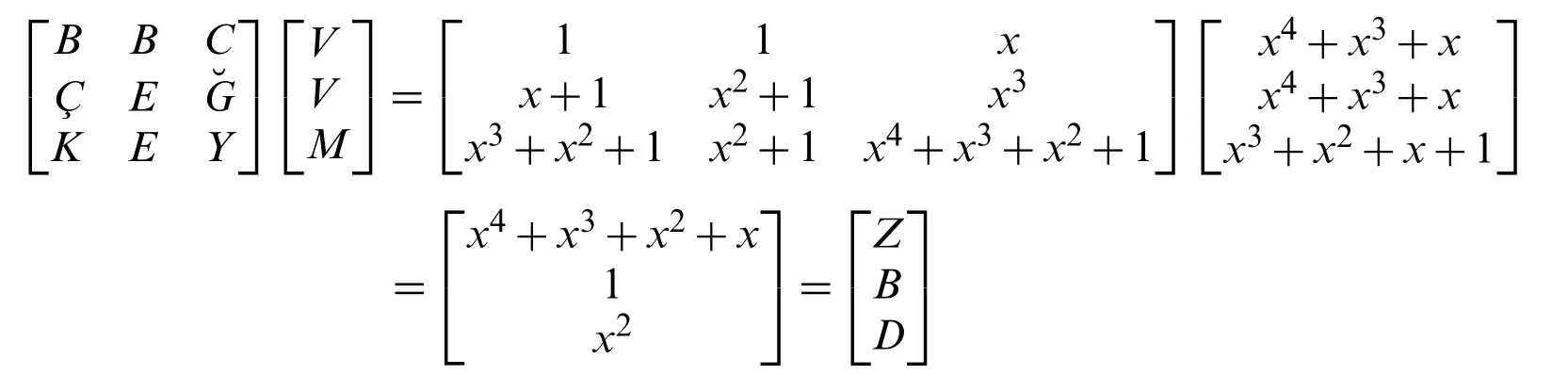
Since we have 2 letters left, we can use our 2.Key matrix,

It results “VVMKR”→“ZBDX

• Step 4:We get

Z+T1(x)=x4+x3+x2+x+1=Q

B+T2(x)=1+x2=E

D+T3(x)=x4+x2+x=S

X+T4(x)=x4+x2+x+1=T

whereTn(x)is anthTribonacci polynomial.

It results “ZBDX”→“”.

Application to the Decoding Algorithm:

• Step 1:We can get as

Q+T1(x)=x4+x3+x2+x=Z

E+T2(x)=1=B

S+T3(x)=x2=D

T+T4(x)=x4+x3+x2=X

S+T5(x)=x4+x3+1=

whereTn(x)is anthTribonacci polynomial.

It results “”→“”.

• Step 2:We multiply the message matrix we just obtained by inverse of the 1.Key matrix.

Since we have 2 letters left, we can use our 2.Inverse key matrix.

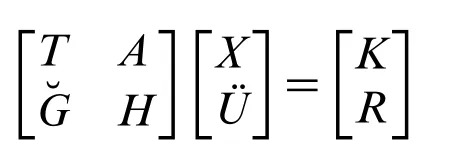
It results “ZBDX”→“VVMKR”.

• Step 3:We can obtain the matrixaccording to thekandnvalue we have chosen.

Fork=3 andn=5; we get as

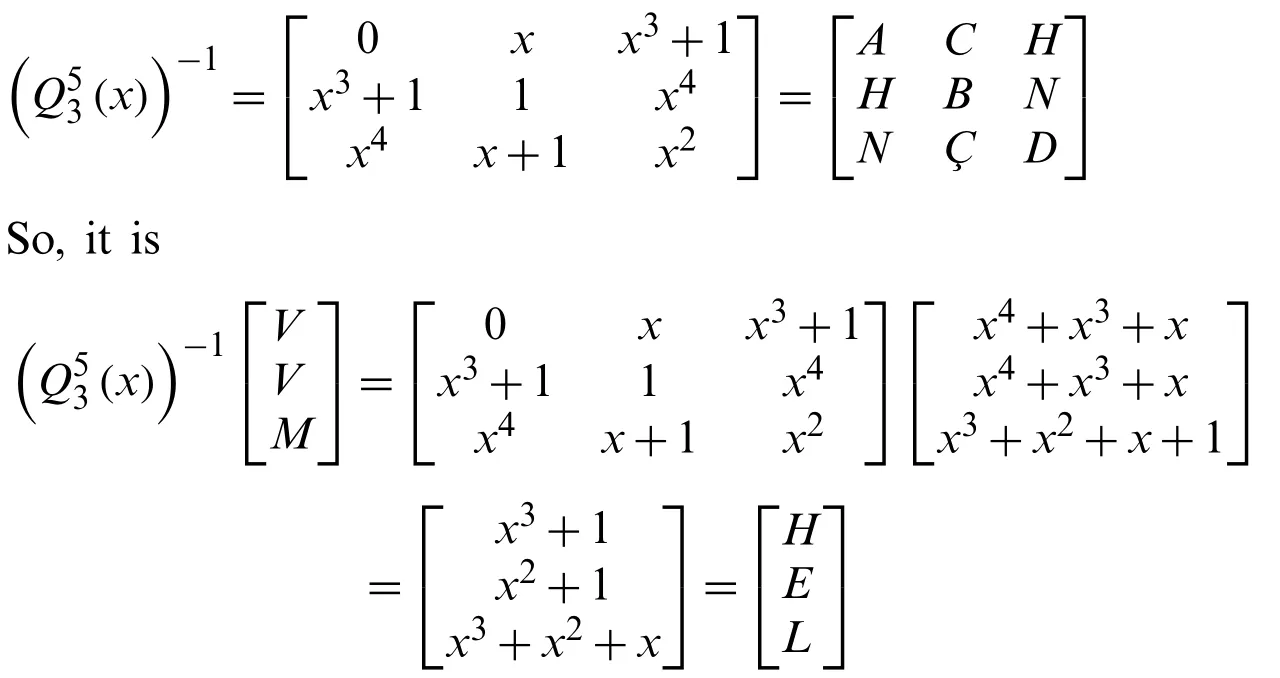
Since we have 2 letters left, we can getfork=2 andn=5 as

It results “VVMKR”→“HELLO”.

We have handled the example given in [20] again with the algorithm we created.The correct result was obtained as a result of the operation we have done.In addition, the encryption process performed with 2×2 block matrices in the other study was performed faster and easier with this method.

Example 2:Let us consider the message text for the following:

“PUBLIC”

Application to the Coding Algorithm

• Step 1:“PUBLIC”is 6 letters.In his example, we encrypt process by choosingn=6 (We can choose n arbitrarily.We do not have to choose the same number of letters as the number of n in our message text to be encrypted).

• Step 2:Fork=4 andn=6, we can use Tetranacci polynomials for encryption.We can get as

It is known that

19=(10011)=x4+x+1=P

24=(11000)=x4+x3=U

1=(00001)=1=B

14=(01110)=x3+x2+x=L

10=(01010)=x3+x=I

2=(00010)=x=C

So, it is

Since the word “PUBLIC” has 6 letters, we divide it into blocks of 4×1 and 2×1.So now:

We encrypt the 2×1 block with the usual Fibonacci polynomial matrix.

We can get as

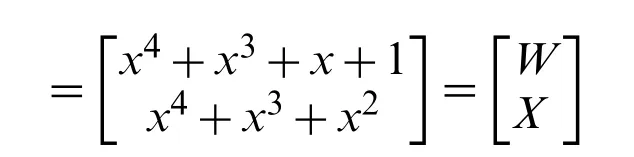
It results ‘PUBLIC’→‘ZÇLMWX’.

• Step 3:We multiply the message matrix we just obtained by the invertible 1.Key matrix.

Turn into blocks of 3s and multiply with the key matrix.

Since we have 3 letters left, we can use our 1.Key matrix again.

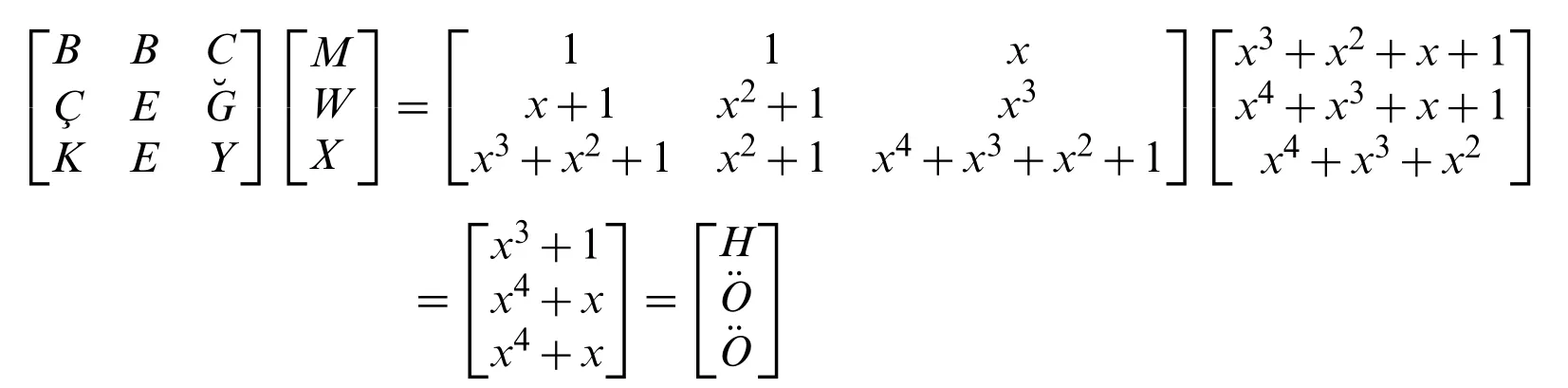
• Step 4:We get

whereF(4)n (x)is a Tetranacci polynomial.

Application to the Decoding Algorithm

• Step 1:We can get as

whereF(4)n (x)is a Tetranacci polynomial.

• Step 2:We multiply the message matrix we just obtained by inverse of the 1.Key matrix.

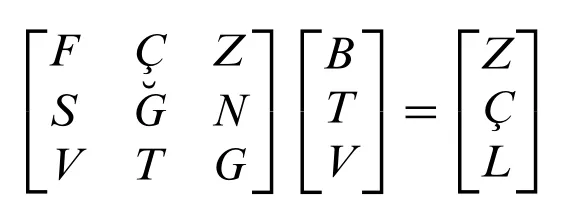
Since we have 3 letters left, we can use our 1.Inverse key matrix again.

• Step 3:We can obtain the matrixaccording to thekandnvalue we have chosen.

Fork=4 andn=6; we get as

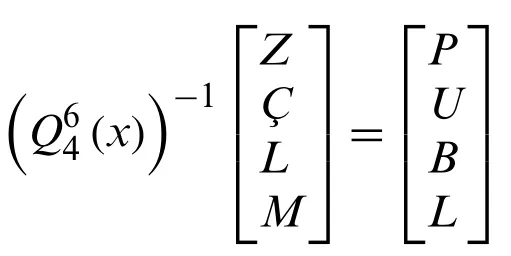
and fork=2 andn=6

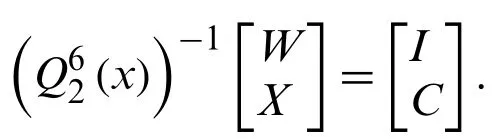
It results “”→“PUBLIC”.

3 Conclusion

AES (Advanced Encryption Standard)is a standard offered for encryption of electronic data.The AES cipher is almost identical to the block cipher Rijndael.The Rijndael block and key size vary between 128, 192 and 256 bits.However, the AES standard only calls for a block size of 128 bits.Hence, only Rijndael with a block length of 128 bits is known as the AES algorithm.In the remainder of this page, we only discuss the standard version of Rijndael with a block length of 128 bits.

The Rijndael algorithm perform encryption with the help of polynomials in Galois fields.We have obtained a new encryption algorithm by generalizing the previous studies.In this paper,we generalized the encryption algorithm given in [20] and studied the encryption made with the 2×2 type block matrix operation to thek×ktype in Galois field.We redefined the elements of k-order Fibonacci polynomials sequences using a certain irreducible polynomial in our cryptology algorithm.The algorithm consist of four steps as in the AES-like encryption algorithm.The encryption algorithm defined in this algorithm is a symmetric-key algorithm in which the keys used in both encryption and decryption of encrypted text are related to each other.The encryption and decryption keys are the same like AES.So, this cryptology algorithm is called AES-like cryptology algorithm on the k-order Fibonacci polynomials.In this way, researchers can perform the encryption process based on arbitrary choices.

In this paper, we present the mathematical basis for understanding the design rationale and the features that follow the description itself.Then, we define AES-like encryption by giving the encryption method and its implementation.

Funding Statement:This work is supported by the Scientific Research Project (BAP)2020FEBE009,Pamukkale University, Denizli, Turkey.

Conflicts of Interest:The authors declare that there are no conflicts of interest regarding the publication of this article.