基于自私兽群算法优化多尺度熵的区域降水复杂性分析
2022-04-12刘东王椿庆张亮亮
刘东, 王椿庆, 张亮亮
(1.东北农业大学 水利与土木工程学院,黑龙江 哈尔滨 150030; 2.农业部农业水资源高效利用重点实验室,黑龙江 哈尔滨 150030; 3.黑龙江省寒区水资源与水利工程重点实验室,黑龙江 哈尔滨 150030)
气候变化对人类社会的巨大影响,受到了世界各国的普遍关注。降水作为影响人类和陆地生态系统的重要气候因素之一,一直是各国学者热衷研究的对象[1-2]。降水作为区域自然地理特征的重要表征要素,是水文预报的重要依据。然而,降水受到多重水文要素、季节性变化以及空间分布的影响,使其呈现出显著的不确定性和明显的波动变化等复杂性特征[3]。人口、工农业以及经济发展对水的需求与日俱增,降水的复杂性特征导致降水的强时空变异性,这既增加了降水预报和水资源管理的难度,又增加了旱涝灾害的发生几率,严重影响着人民的生产和生活。同时,降水对植被、土壤理化性质、地表径流均具有很大的影响,降水复杂性给生态环境带来诸多影响。基于此种背景,探究降水复杂性测度改进方法,识别区域降水的复杂性特征,探索导致降水复杂性的可能诱因,对实现降水的精准预测与趋势把握、旱涝灾害的预防和整治以及人民生产和生活的有序进行都有着十分重要的意义。
随着复杂性科学的快速发展,相关理论得到发展和完善,这为探索降水复杂性测度问题提供了有效的理论基础。近年来,熵、分形、混沌等理论被广泛应用于时间序列的复杂性测度分析中[4]。熵因为其简单实用及在灵敏度和抗噪性计算中的优势,在时间序列复杂性测度领域中备受研究者的青睐[5]。余冲等以信息熵为手段,对湖北省各气象站1951—1996年间的月降水资料进行分析,揭示了降水的时空变化规律和发展趋势[6]。薛联青等将改进的样本熵运用到湘江流域的降水和径流时间序列复杂性分析中,发现了样本熵能有效识别时间序列的动力学特征[7]。ZHANG Liangliang等利用样本熵、小波熵、排列熵和模糊熵对黑龙江省降水复杂性进行分析,结果发现,样本熵具有更高的稳定性和可靠性[3]。
样本熵由RICHMAN Joshua S首次提出,它具有不依赖数据长度、较高一致性以及对缺失数据不敏感等优点[8]。CHOU Chien Ming等应用样本熵分析了不同尺度的降雨和径流时间序列复杂性[9]。XAVIER Sílvio Fernando Alves Jr等利用样本熵分析了巴西帕拉伊巴州降水序列复杂性特征[10]。COSTA M等在样本熵的基础上对时间序列进行了粗粒化处理,提出了多尺度熵理论[11]。BALZTER Heiko等利用多尺度熵分析气候时间序列数据,结果显示,相比传统方法,利用多尺度熵方法可以发现相关的额外有价值的信息[12]。ZHOU Yu等利用多尺度熵方法研究了水库对河流流量的影响,结果显示,多尺度熵方法可以在多个尺度进行分析,并且能够很好地探索水文过程的非线性特性,该方法所得结果不受周期趋势的影响[2]。已有研究发现,多尺度熵具有稳定、精确且能够展现序列多维性的优点,实现起来更加简单,实现过程容易理解13-14]。
参数的选取是多尺度熵估计相对准确的关键,已有的研究中[4,10]均以穷举法方式来寻找最优参数。穷举法虽然简单和易于理解,但是存在繁冗的计算过程。近年来,智能优化算法被广泛用于参数寻优的过程中,取得了良好的效果。自私兽群(Selfish Herd Optimization,SHO)算法是FAUSTO Fernando 等在2017年提出的一种群智能优化算法[15]。自私兽群(SHO)算法是基于Bill Hamilton提出的自私兽群理论来表达猎物和捕食者的狩猎关系,通过模拟捕食者捕食猎物时捕食者和猎物位置变化来实现最优解的搜索,该算法在寻优过程中具有精度高和鲁棒性强的特点[16]。
ZHAO Ruxin 等在SHO算法中加入混沌策略,并利用其来对IIR数字滤波器进行参数优化,在求解IIR系统辨识问题时取得了较好的结果[17]。JENA Narendra Kumar等利用SHO算法优化了PID控制器的动态性能[18]。
本文具体研究目标如下:
1)运用自私兽群(SHO)算法率定多尺度熵的最佳参数;
2)分析区域降水复杂性空间特征及其可能成因;
3)评估基于自私兽群(SHO)算法的区域降水复杂性多尺度熵测度模型性能。
1 研究区域与数据来源
1.1 研究区域
北大荒农垦集团有限公司建三江分公司地处世界三大黑土带之一的三江平原腹地,位于黑龙江、乌苏里江汇流的冲积河间地带。地理坐标为北纬46°49′~48°12′、东经132°31′~134°32′,如图1所示。建三江分公司下辖的15个农场是中国重要的粮食产区和商品粮种植基地,同时是世界高纬度粳稻种植面积最大的地区[19]。由于降水的复杂性特征给土壤、地表径流等农业环境带来的诸多困扰,影响农业气象预报和农业灌溉,从而妨碍粮食增产增收和农业的健康发展,故有必要开展建三江分公司下辖15个农场(研究区域)的降水复杂性测度分析。
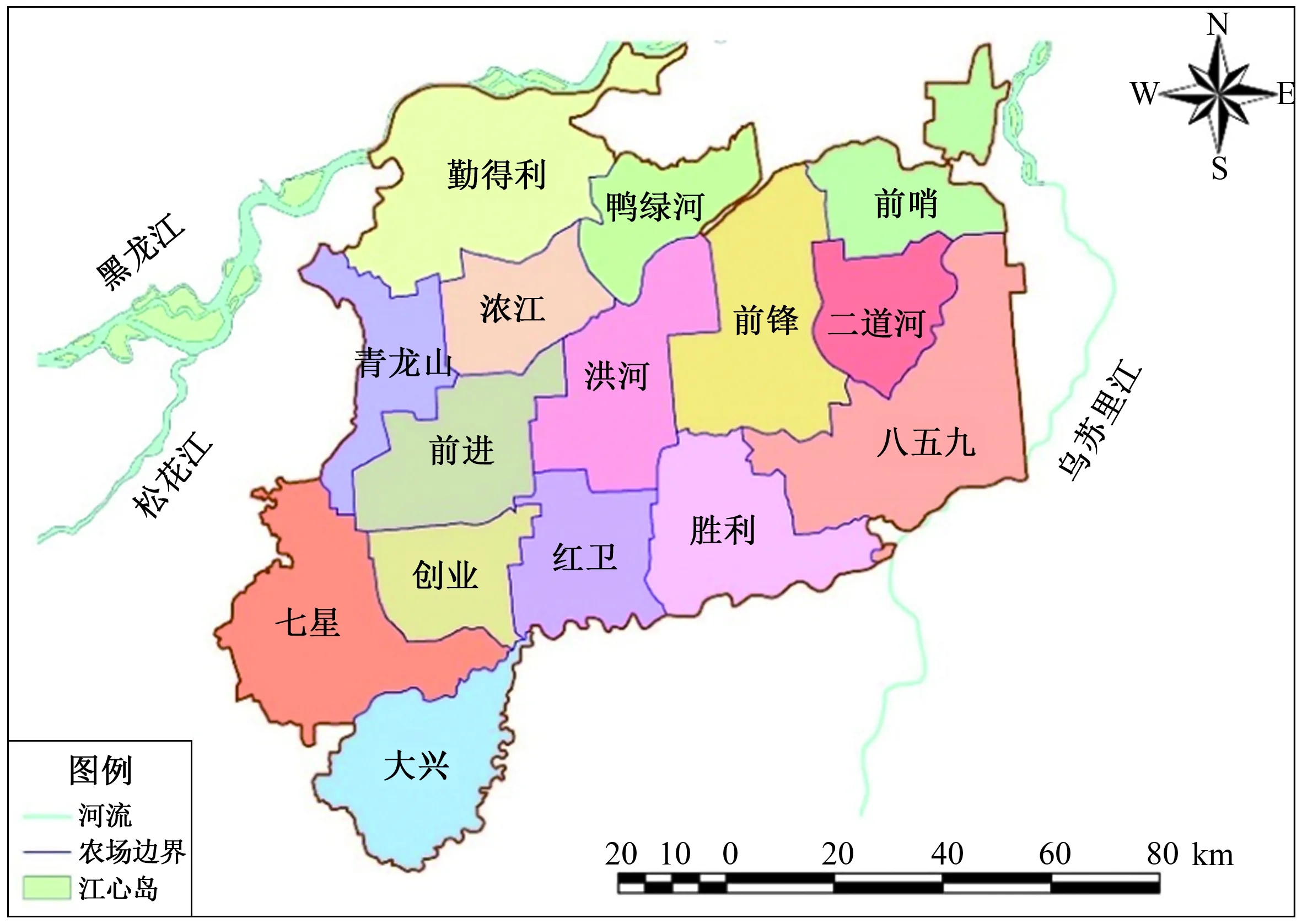
图1 建三江分公司行政区划图
1.2 数据来源
从中国北大荒农垦集团有限公司建三江分公司收集到建三江分公司各农场1997—2018年(年数n=22)逐月降水监测资料,用于后续复杂性研究;从《建三江农垦统计年鉴》(1997—2016年)、《建三江农垦年鉴》(2017—2019年)收集整理得到该区的森林覆盖率、水域面积、人口密度等自然地理数据以及经济社会发展统计资料,用于后续降水复杂性可能原因分析。
2 研究方法
2.1 多尺度熵
多尺度熵是在样本熵的基础上,对原始的时间序列进行粗粒化处理,使其在保留样本熵对缺失数据不敏感、较高一致性等优点[20]的同时体现时间序列的多维性。多尺度熵求取的具体步骤如下:
设原始的时间序列为:a(1)、a(2)、a(3)、……、a(N)。3个参数分别为:尺度因子t、嵌入维数m、相似系数r。
步骤1对原始时间序列进行粗粒化处理,得到新时间序列,如下:
(1)
新时间序列的长度P=int(N/t)。

Bt(i)=[b(t)(i),b(t)(i+1),…,b(t)(i+m-1)]。
(2)
式中i=1、2、…、P-m+1。
步骤3定义序列Bt(i)与Bt(j)对应元素最大差值的绝对值为二者之间的距离,如下:
D[Bt(i),Bt(j)]=max(|Bt(i+h)-Bt(j+h)|)。
(3)
式中:h=0、1、…、m-1;i、j=1、2、…、P-m+1;i≠j。
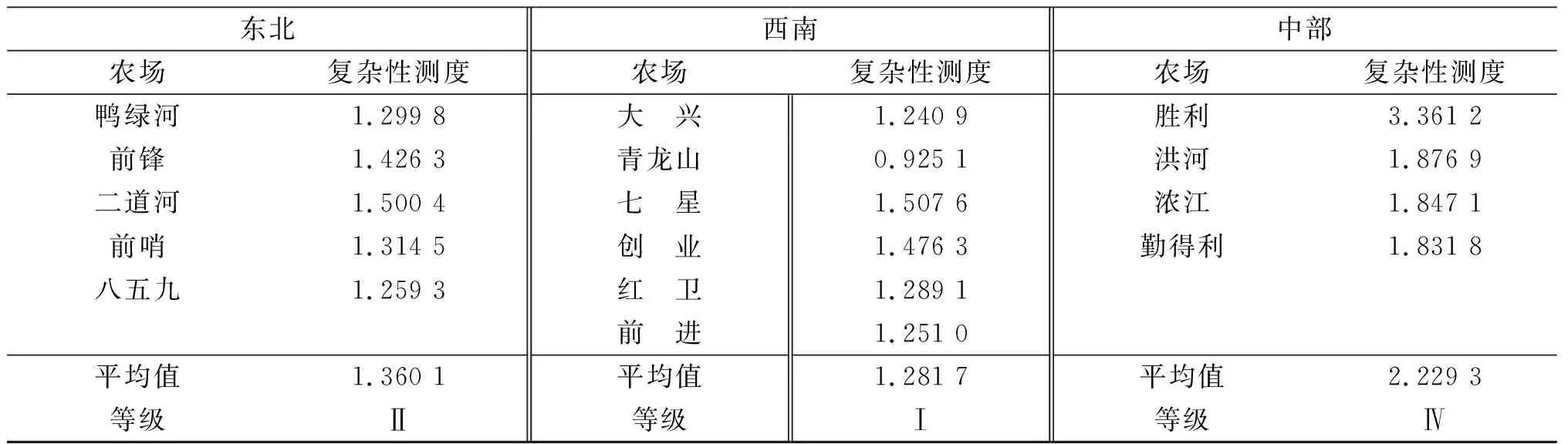
步骤4计算距离D小于r的个数N{D[B(t)(i),B(t)(j)] (4) (5) 步骤6将维数增加1,变为m+1,重复步骤2—5,得到Et,m+1(r)。 步骤7定义多尺度熵为: (6) 自私兽群算法是通过模拟狩猎者捕食猎物来寻找最优值的一种群智能优化算法[21]。具体的运行步骤如下: 步骤1随机生成动物种群。在参数边界内随机生成动物种群,计算公式如下: (7) 研究发现,猎物群体占动物种群的70%~90%[15],故猎物数量和狩猎者数量如下: Nh=floor(N·rand(0.7,0.9)), (8) Np=N-Nh。 (9) 式中:Nh为猎物数量;Np为狩猎者数量;N为动物种群数量。 步骤2生存价值是用来表示动物群体中所有个体能够生存下来的能力[16],计算公式如下: (10) 式中:SV为个体生存价值;f代表目标函数,fbest和fworst分别代表目标函数的最佳值和最差值。 步骤3猎物群的运动。 1)猎物群领袖的运动。猎物群的领袖往往具有最大生存价值[22]。猎物群领袖的位置L更新公式如下: (11) 式中:a为[0,1]区间的随机数;φ代表个体之间的吸引力;D为猎物群中危险位置;A为猎物群中最优位置。 2)猎物群跟随者和猎物群逃脱者的运动。猎物群的跟随者(F)是选择跟随猎物群体的成员,猎物群脱逃者(T)是选择脱离群体的成员,而猎物群的跟随者分为优势猎物群跟随者(FB)和劣势猎物群跟随者(FW)[23]。其位置更新公式如下: (12) T=T+2(βφT,B(A-T)+γ(1-SVT)ε)。 (13) 式中:β、δ、γ均为[0,1]内的随机数;Z表示局部最优个体;M表示猎物相对安全位置;ε表示空间解中的随机方向;φF,L为个体与猎物群领袖之间的吸引力;φF,C为个体与局部最优个体C之间的吸引力;φF,M为个体与相对安全个体M之间的吸引力;φT,B为个体与全局最优个体B之间的吸引力。 步骤4狩猎者的捕食运动。狩猎者(PA)寻找猎杀半径内的猎物,并以赌轮盘方式选择捕食,其位置更新公式如下: PAi=PAi+2ρ(R-PAi)。 (14) 式中:ρ为[0,1]中的随机数;R是被捕食的猎物。 步骤5猎物群恢复阶段。通过交配概率选择猎物群的个体,被选择的个体通过交配产生的新生猎物取代被猎杀的猎物。交配操作过程如下: snew=mix([sr1,sr2,…,srn])。 (15) 式中:mix用于从不同生存个体中选择维度组件;s表示在猎杀中幸存的个体。 以尺度因子t、嵌入维数m、相似系数r为优化目标,以区分度为目标函数,利用自私兽群算法对t、m、r进行迭代优化,具体操作步骤如下: 步骤1初始化自私兽群搜索个体,即初始化t、m、r。 步骤2以区分度公式为目标函数,区分度Z的计算公式如下: (16) 式中:x为评价对象个数;y′为y标准化后的评价结果。 步骤3初始化算法的参数,包括自私兽群数量及比例、搜索空间、迭代次数、算法终止条件等。 步骤4分别利用公式(10)(17)计算个体的生存价值与适应度值,公式(17)为对评价对象的评价结果进行标准化处理的公式,具体如下: (17) 步骤5依据公式(11)(12)(13)进行猎物群个体的移动,依据公式(14)对狩猎者群捕食运动。 步骤6依据公式(15)进行种群恢复操作。 步骤7判断算法是否达到终止条件,若满足则转到步骤8,否则重复执行步骤4—6。 步骤8输出最优的自私兽群最优个体的t、m、r最优值。 运用自私兽群算法优化多尺度熵评价降水复杂性测度的流程如图2所示。 图2 降水复杂性测度评价流程 区分度理论适用于区别不同水平的评价对象,通常区分度越大,越能将不同的评价对象区分开来[4, 24],具体步骤如下: 步骤1对现有的x个评价对象的评价结果y进行降序排列 。 步骤2由式(17)对评价对象的评价结果进行标准化处理。 步骤3由式(16)对降水复杂性测度进行标准化后的区分度计算。 建三江分公司下辖15个农场1997—2018年间的逐月降水变化的线性拟合结果见表1,逐月降水变化及其趋势线如图3所示。 表1 建三江分公司各农场逐月降水序列拟合趋势线决定系数 由图3可知,月降水序列呈现出明显的波动性和周期性,因为月降水受到明显的季节变化影响,一年内5—8月份的降雨量偏多,其他月份的偏少。为判断降水变化是否具有趋势性,为15个农场的月降水时间序列添加趋势线,通过观察月降水拟合趋势线(图3),发现这15个农场的降水拟合趋势线基本为水平线。 图3 建三江分公司各农场逐月降水序列变化曲线及拟合趋势线 由表1可知,月降水拟合趋势线与月降水实测值的决定系数均小于0.01,通常情况下决定系数越大拟合效果越好,表明建三江分公司下辖的15个农场的月降水变化不具备明显的趋势性,月降水变化具有显著的复杂性特征。 3.2.1 复杂性测度模拟等级区间 为了更加直观地观察建三江分公司下辖的各个农场的月降水复杂性测度情况。现对各个农场的月降水复杂性测度进行等级划分。因为自然间断法能够识别分类间隔,恰如其分地对相似值进行分组并能保持各组差异最大化。利用ArcGIS内置分类方法中的自然间断法对各个农场的复杂性测度进行等级划分,并将其分为Ⅰ—Ⅳ 4个等级,具体见表2,其中等级越高表示具有较高程度的复杂性。 表2 复杂性测度等级划分标准 3.2.2 降水复杂性空间特征分析 设置自私兽群算法[16]的基本参数:初始种群数量N=50、迭代次数itern=50、优化维度dims=3、猎物种群的比例(为0.7~0.9之间的随机数),根据已有研究经验[25]设置多尺度熵的参数搜索范围,尺度t为1~10、嵌入维度m=1~3、r=(0.10~0.25)SD,SD为降水时间序列的标准差。利用自私兽群算法寻优计算得出区分度最大时的尺度因子t、嵌入维数m、相似系数r,参数值组合为t=5、m=2、r=6.804 09,区分度为1.215 2。将建三江分公司下辖的15个农场1997—2018年的月降水数据输入到优化后的多尺度熵中,计算得出在此参数组合下的各个农场的月降水复杂性测度,并划分各个农场的复杂性测度等级,结果见表3。 表3 最优参数组合下各农场复杂性测度结果 由表3可知:八五九、大兴、青龙山、前进、红卫、前哨、鸭绿河7个农场的月降水复杂性测度等级为Ⅰ级,七星、创业、前锋、二道河4个农场的月降水复杂性测度等级为Ⅱ级,这些结果表明这11个农场的月降水变化的复杂性不高;勤得利、浓江、洪河3个农场月降水复杂性测度等级为Ⅲ级,胜利农场的月降水复杂性等级达到Ⅳ级,这4个农场的月降水复杂性变化最为明显,尤其是胜利农场的月降水复杂性达到最高的Ⅳ级。由计算所得熵值进行月降水复杂性测度排序,由高到低的顺序为:胜利>洪河>浓江>勤得利>七星>二道河>创业>前锋>前哨>鸭绿河>红卫>八五九>前进>大兴>青龙山。 为了更加直观地观察建三江分公司下辖各农场月降水复杂性的空间分布情况,根据表3的复杂性测度结果绘制各个农场的月降水复杂性测度等级空间分布,如图4所示。 图4 建三江分公司各农场月降水序列复杂性等级空间分布 由图4可知,建三江分公司下辖15个农场的月降水复杂性测度具有明显的空间变异特征,月降水复杂性测度等级为东北和西南各农场的较低,中部各农场的复杂性测度较高。 为了直观地了解月降水空间复杂性分布情况,分别计算建三江分公司辖区东北、中部、西南部的各个农场月降水的平均复杂性测度,结果见表4。 表4 建三江分公司各农场月降水序列复杂性分区统计计算结果 由表4可知:中部农场具有最高的月降水复杂性测度,胜利农场复杂性测度为3.361 2,等级达到最高的第Ⅳ等级,表明中部的各农场的月降水复杂性变化最为显著。降水复杂性测度越高的农场往往降水动力学结构越复杂,降水的可预测性就越低,造成洪涝、干旱灾害的可能性也就越大,应强化中部农场降水监测水平,建立实时的灾害监控网络,完善应急管理预防系统,配置相应的抗灾管理人员与机构,降低干旱和洪涝灾害对农业的影响[4]。东北部的各农场月降水平均复杂性测度为1.360 1,等级为Ⅱ级,为第二高。西南部各农场的月降水复杂性测度最小,为1.281 7,等级为Ⅰ级,相对来讲降水的动力学结构较为简单,降水的可预测性也较高。 由于降水具有复杂性特征,不能单一方面考虑降水的成因。XU Jianhua等在分析新疆降水复杂性时发现降水分布的空间复杂性来源于复杂的地形[1]。ZHANG Liangliang等在分析黑龙江省降水复杂性时,计算了耕地、林地、草地、水域、居民用地、未利用地、人口数量、农业产值、工业产值与月降水复杂性的相关系数,试图揭示影响黑龙江省降水复杂性的潜在因子[4]。缠佳悦分析哈尔滨降水复杂性成因时着重考虑了地形和人口密度、工业产值、水旱田灌溉面积比重等人类活动等因素[26]。 本文从自然因素和人类因素两方面考虑导致降水复杂性的可能诱因。自然因素方面考虑森林覆盖率和水域面积。因为建三江分公司辖区地形基本上为平原,地势起伏变化不大,故不考虑地形的影响。人类因素方面考虑人口密度。因为建三江分公司辖区的农业发达,故着重考虑耕地面积比例。建三江分公司下辖的农场的农田灌溉率基本上为100%,分析灌溉率与降水复杂性关系的可研性较差。建三江分公司下辖的各农场普遍采用机井灌溉,考虑灌溉可能会对气候造成影响,故探究机井数量与降水复杂性的关系。各影响因素与降水复杂性的相关系数见表5。 表5 降水复杂性与其影响因素的相关系数 通过统计分析发现,人类因素均与降水的复杂性呈负相关,其中月降水复杂性与人口密度相关性最强,和耕地面积比例的相关性次之,与机井数量的相关性最弱。人类在改造自然的过程中,会使人类因素向适应农业生产的方向发展,从而降低了降水的复杂性。可见,人类活动是影响降水复杂性的重要因素,对降水复杂性的空间格局起着不可忽视的作用,相比较而言,森林覆盖率和水域面积对降水复杂性的影响较小。通过分析1997—2018年建三江分公司辖区农场的森林覆盖率和水域面积的情况发现,森林覆盖率和水面面积年平均变幅分别为0.17%和-0.009%,多数农场的森林覆盖率和水域面积变化较小。建三江分公司辖区农场的土地多为农田,多数农场的森林覆盖率和水面率不高,故森林覆盖率和水面率对降水的复杂性影响也相对较小。 为了验证自私兽群算法的搜索精度和搜索效率,设置t=1~10、m=1~3、r=(0.10~0.25)SD,t的变化步长为1,m的变化步长为1,r的变化步长为0.01,以区分度为目标函数进行计算,并与自私兽群算法的寻优过程进行对比,其结果见6。 由表6可知,自私兽群算法与穷举法在寻优精度上相同,但是在寻优速度上存在显著差异。自私兽群算法的寻优效率是穷举法的11倍,寻优速度显著提升,并且能够保证寻优精度,表明利用自私兽群算法来进行多尺度熵寻优具有一定优势。 表6 结果对比分析 自复杂性科学兴起并广泛应用于各类学科以来,区域降水复杂性特征成为研究的热点问题[27]。熵作为不确定性的重要理论,被引入到降水复杂性测度的应用中。学者们为此进行了不懈的探索。刘萌在利用模式熵对研究区进行复杂性测度分析时,利用前人经验选取嵌入维数,并在阈值的经验取值区间以0.01的步长寻找最优值[28]。ZHANG Liangliang等研究发现样本熵在研究复杂性测度中更具适用性,之后采用区分度理论优化样本熵,提高了样本熵对降水复杂性测度的寻优能力,在参数寻优方面仍然在经验区间内以0.01的步长寻找阈值[3-4]。本文采用的多尺度熵是在样本熵优点的基础之上,通过对原始时间序列的处理,使其能够体现时间序列的多维性,并且不依赖数据长度而拥有良好的一致性[29]。大多数学者在运用熵理论时大多依赖前人经验,在参数寻优过程中,在经验区间内以等步长形式寻找最优值,虽然简单易于理解,但是存在大量的繁冗计算过程。近年来,智能优化算法被广泛应用于学术领域,本文采用的自私兽群(SHO)算法通过模拟捕食者的狩猎过程寻找多尺度熵的最优参数组合,整个寻优过程用时约为15 s,寻优效率得到了较大提升。 由于降水受到地形、气候、植被和人类活动多重因素的影响,从而造成降水空间的异质性。本文在探究导致降水复杂性潜在诱因时,考虑了人类因素和自然因素两方面的影响。由于建三江分公司是重要的粮食产区和商品粮种植基地,该辖区农业十分发达,故本文着重考虑了农业相关因素与降水复杂性的关联性。又因为建三江分公司所在地区地处三江平原腹地,故未考虑地形因素的影响,其内部森林和水域面积不大,故自然因素对该辖区降水复杂性影响相对较小。但是,单单对建三江分公司辖区小范围尺度分析降水复杂性的诱因,难以完全理清降水复杂性的潜在影响因素,现有资料限制,后续可做进一步探索。 本文将多尺度熵作为衡量建三江分公司辖区农场降水复杂性的指标,综合反映出该辖区农场降水复杂性的空间格局,研究结果对进一步了解建三江分公司下辖各农场降水复杂性特征具有重要意义。其主要结论如下: 1)采用自私兽群优化算法并基于区分度理论对多尺度熵的参数进行寻优,利用优化后的多尺度熵分析了1997—2018年建三江分公司下辖的15个农场的月降水复杂性。 2)通过分析发现,这15个农场的月降水复杂性测度从高到低的次序是:胜利>洪河>浓江>勤得利>七星>二道河>创业>前锋>前哨>鸭绿河>红卫>八五九>前进>大兴>青龙山,利用ArcGIS软件对降水复杂性测度等级进行了空间化展示,发现中部农场的复杂性测度最高,东北部农场的次之,西南部农场的复杂性测度最低。 3)为了探究造成降水复杂性的可能原因,将影响降水复杂性的因素分为人类因素和自然因素,其中人类因素包括人口密度、耕地面积比例和机井数量,自然因素包括森林覆盖率和水域面积,通过分析各因素和降水复杂性测度的相关系数发现,人类规律性改造自然活动会降低降水的复杂性。 4)随着气候检测技术手段的不断进步以及大数据时代的来临,地区乃至国际间的合作不断增强,区域网络的互联互通、资料数据的共用共享,未来将从简单孤立的小范围、单区域扩展到复杂联系的大尺度、多区域来探究导致降水以及气候复杂性的原因及影响因素。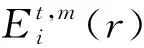
2.2 自私兽群算法

2.3 模型构建法
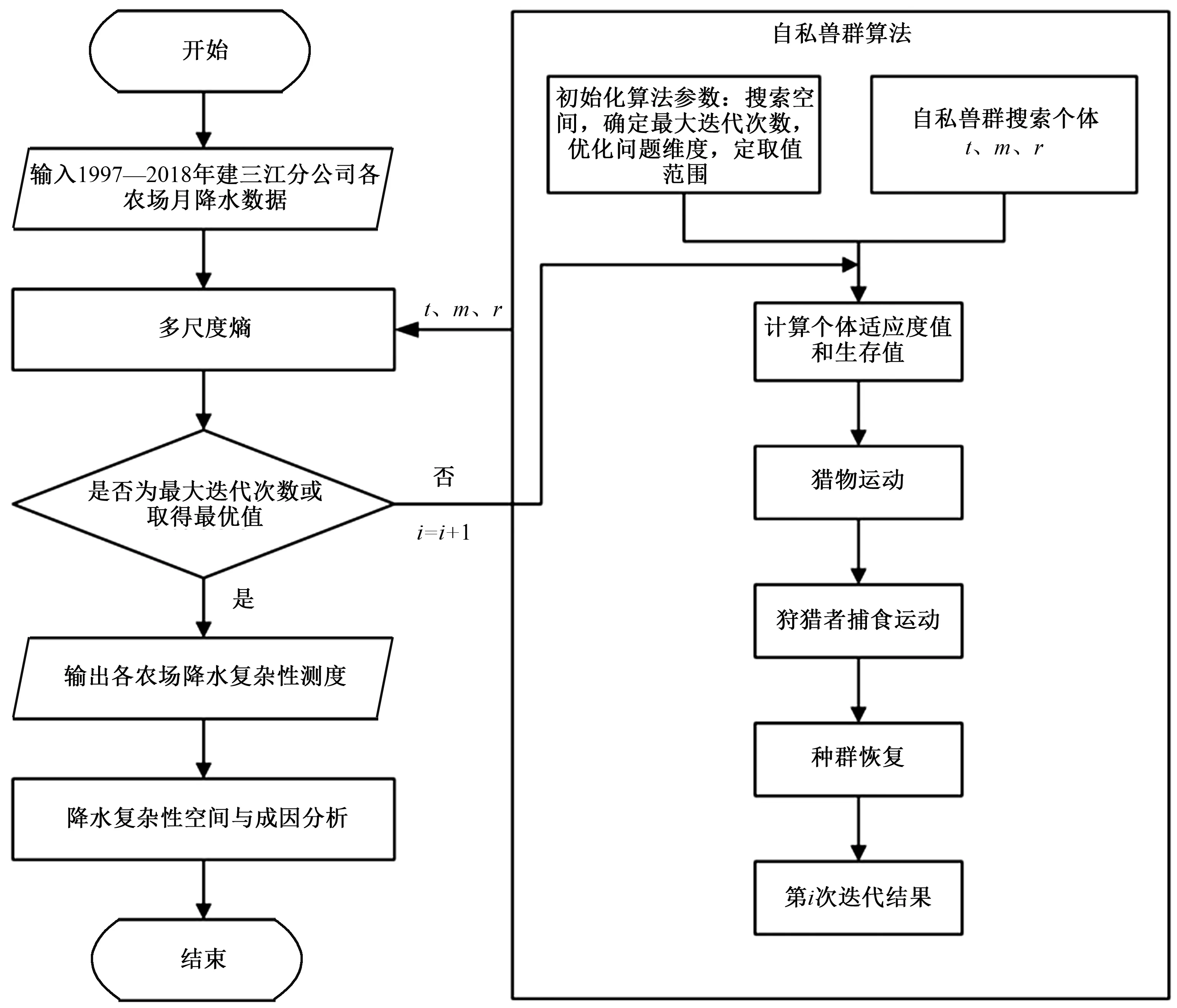
2.4 区分度理论法
3 结果与分析
3.1 建三江分公司下辖各农场月降水序列复杂性特征初步判别

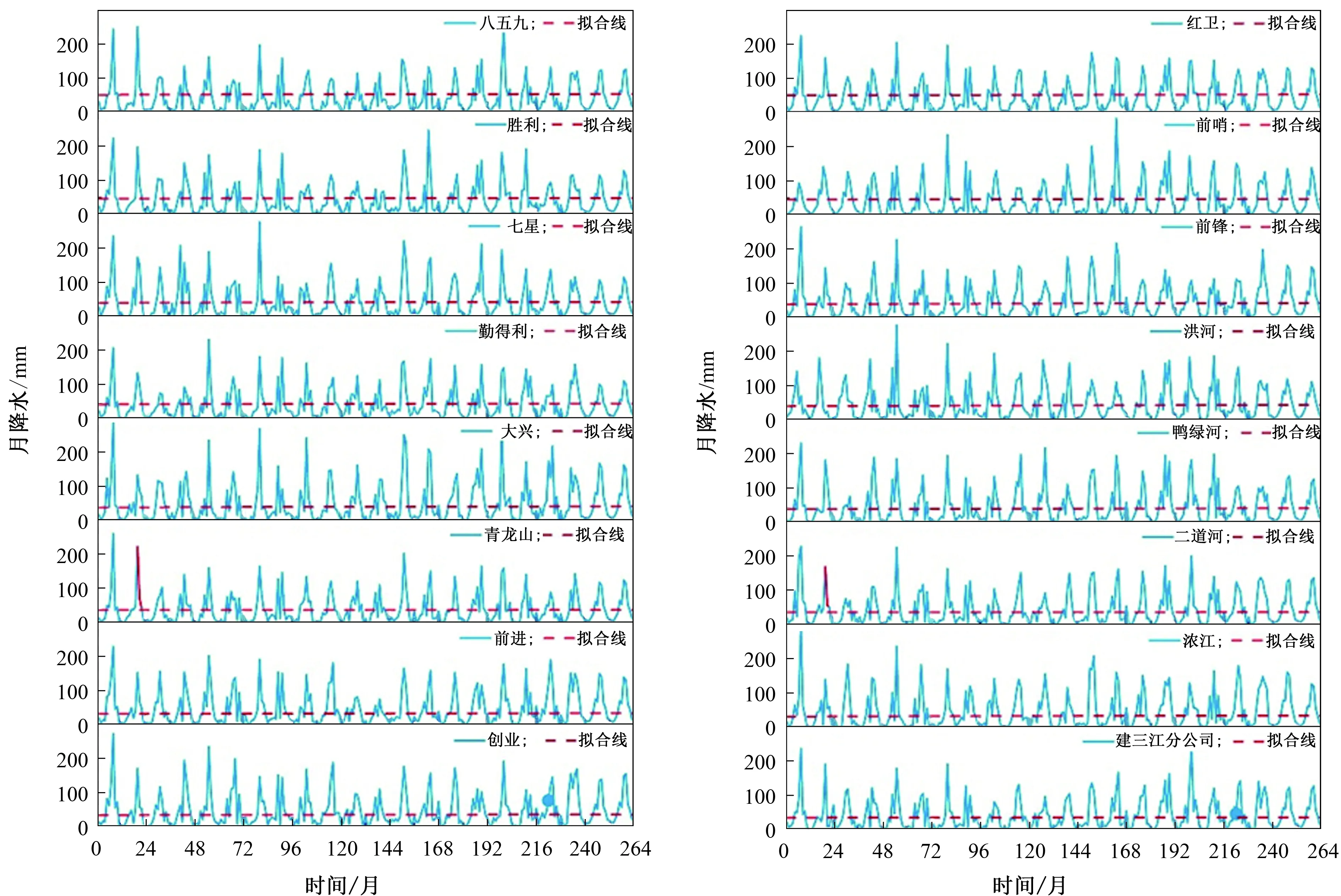
3.2 建三江分公司下辖各农场的月降水序列复杂性测度分析



3.3 降水复杂性可能成因分析

4 讨论
4.1 模型性能对比分析

4.2 与已有成果的对比分析
5 结论
