融合空间位置与结构信息的压缩感知图像重建方法

林乐平，周宏敏，欧阳宁*

（1.认知无线电与信息处理省部共建教育部重点实验室（桂林电子科技大学），广西桂林 541004；2.桂林电子科技大学信息与通信学院，广西桂林 541004）

0 引言

压缩感知理论［1］是一种新兴的信息获取与信号处理领域的理论，可以充分利用信号中的稀疏性信息，在远低于奈奎斯特采样频率的情况下，从采样样本中精确地重建原始信号。压缩感知理论在信号处理及相关领域引起广泛关注，并迅速被应用于图像处理［2-3］、网络通信［4］、雷达成像［5］等诸多领域。将压缩感知应用于图像重建，图像采样和压缩编码同步完成，直接得到压缩后的图像，省去中间处理冗余数据的过程，这对于图像数据的采集和传输有着极大便利和优势。在分块压缩感知框架［6］下，图像重建计算资源损耗进一步减少。

随着深度学习的兴起，许多基于深度学习的图像压缩感知重建方法被相继提出。非迭代重建网络（non-iterative Reconstruction Network，ReconNet）［7］是卷积神经网络在分块压缩感知信号重建问题的首次应用；深度残差重建网络（Deep Residual Reconstruction Network，DR2-Net）［8］是ReconNet与残差网络结构［9］的结合，能学习到更深层次的图像特征；基于非局部约束的多尺度重建网络（Multi-scale Reconstruction neural Network with Non-Local constraint，NL-MRN）［10］在每个重建模块中采用非局部操作，用于增强图像中点与点之间的约束性，进一步提高了重建效果；拉普拉斯金字塔重建对抗网络（LAplacian Pyramid Reconstructive Adversarial Network，LAPRAN）［11］在重建端引入拉普拉斯金字塔概念，每个金字塔层将观测值与上一级输出的低分辨率图像进行信息融合，以实现灵活的高分辨率图像重建；练秋生等［12］提出了一种基于多尺度残差重建网络（Multi-Scale Residual reconstruction Network，MSRNet）的压缩感知方法，网络中引入多尺度扩张卷积用于提取图像块不同尺度的特征；Huang等［13］构建了一种端到端的两阶段网络，通过网络学习到采样矩阵，同时级联图像块重建网络和块状伪影去除网络。

相对于传统压缩感知方法，上述基于深度学习的压缩感知图像重建方法在重建速度和重建效果上均有提升，但忽略了结合图像块之间的位置信息。针对低采样率下分块压缩感知重建图像视觉效果不佳的问题，本文提出一种融合空间位置与结构信息的压缩感知图像重建方法（compressed sensing image reconstruction method fusing Spatial Location and Structure Information，SLSI），并构建基于该方法的两支路网络。网络通过线性映射得到图像块的估计值后，用块分组重建支路结合图像结构信息为不同类型的图像块分配不同重建资源，为稀疏度高的图像块数据分配较少的重建资源，为稀疏度较低的图像块数据分配较多的重建资源，进而将图像块估计值拼接所得数据输入全图重建支路，该支路主要通过双边滤波和结构特征交互模块对相邻图像块像素进行信息交互，以减少低采样率下重建图像的空间位置信息丢失，两支路的加权输出值为最终重建全图。

1 分块压缩感知框架

压缩感知理论的主要思想是：当信号在某已知变换域下具有稀疏性，可以用观测矩阵将高维的信号投影到低维空间，通过求解优化问题从少量投影数据中重建出原始图像。相比基于整图的传统压缩观测，分块压缩感知框架的观测矩阵内存消耗更小以及重建过程的计算更简单。在分块压缩感知框架中，假定原始图像信号I是一个IW×IH大小的图像，将其分成L块大小为的互不重叠图像块，图像块中总像素数为B。将每个图像块转换成列向量，所有的块向量组成图像矩阵X=(x1，x2，…，xL)。所有图像块用同一个观测矩阵Φ∈Rm×B进行独立观测，获得图像块的观测向量集合，Y=ΦX=(y1，y2，…，yL)，Y∈Rm×L，m代表图像块对应的观测值元素总数。分块压缩感知图像重建的目标是从观测向量集合Y中获得对图像矩阵X和图像I的重建估计。

2 本文方法

本文构建的两支路网络结构如图1 所示，主要包括线性映射、块分组重建支路、全图重建支路、支路融合这四部分。

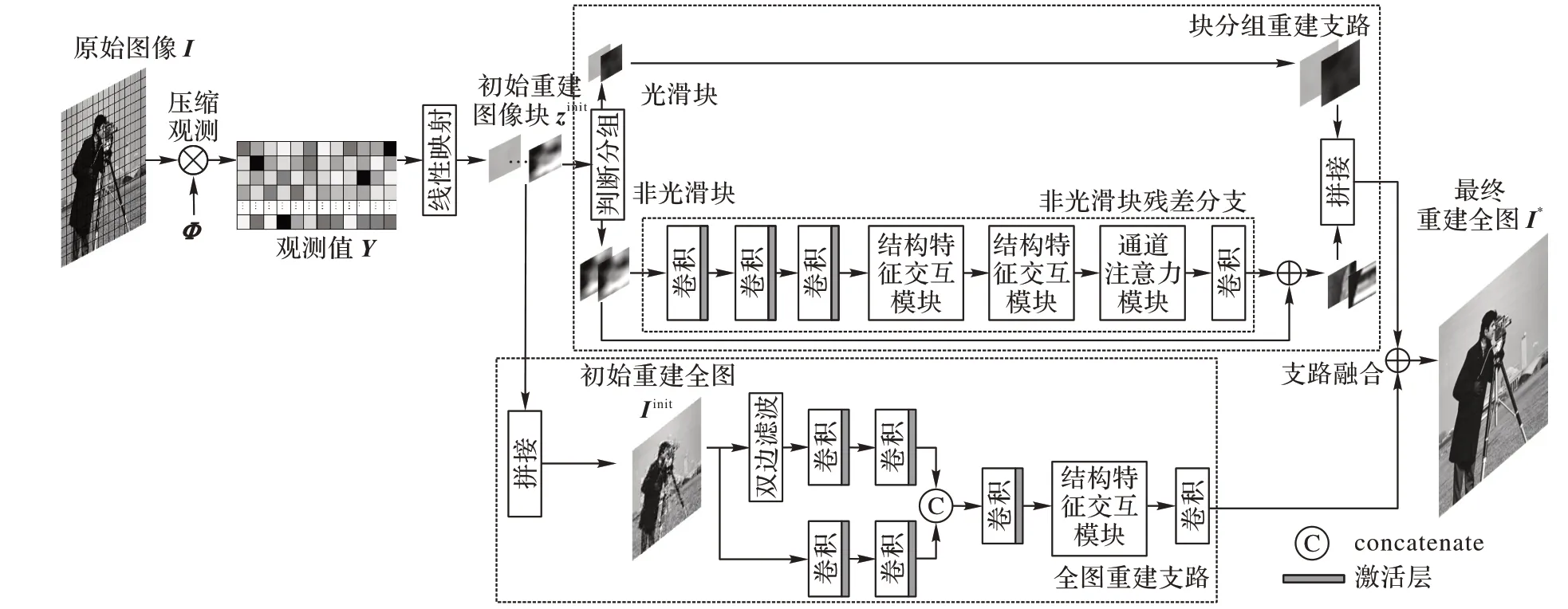
图1 网络结构Fig.1 Network structure

首先，使用线性映射将观测值升维，得到原始图像块的初步估计值；然后，将图像块的估计值输入块分组重建支路，根据样本标准差的均值设定阈值进行分组，分组后的数据进入对应的分组重建分支进行增强重建；同时，图像块的估计值也被输入全图重建支路，将图像块的估计值按照分块顺序进行拼接得到拼接后的全图估计值并开始进行全图重建；最后，对两支路的重建结果进行加权融合，得到高质量的重建图像。另外，观测值数据是在分块策略下通过对数字图像信号进行压缩观测得到，以此模拟真实信号的采样。

2.1 线性映射

线性映射部分由一层全连接和整形操作构成，用于将观测值Y从低维恢复到采样前的高维数据。先通过全连接重建得到X∈RB×L的初步图像矩阵估计)，如式（1）所示：

式中：Ffc(·)表示一个全连接层，层中共有B个全连接神经元，Wfc∈RB×m为全连接层权重。为了便于数据的后续处理，对zfc进行整形（reshape）操作得到初步重建图像块zinit=，也就是图像块的初步估计值，zinit的尺寸为。

2.2 块分组重建支路

块分组重建支路聚焦于每个图像块的重建，主要包括判断分组和分组重建两部分。在分块压缩感知框架的观测阶段采用相同的观测矩阵对每个图像块进行观测。图像的不同区域间结构各异，对图像进行分块后，同样大小的图像块之间包含的能量大小不一样，稀疏度也不一样［14］。根据图像块估计值的数值特性对图像块进行判断分组，以便于对每个组别的图像块设置各自的重建策略：为稀疏度高的图像块数据分配较少的重建资源，为稀疏度较低的图像块数据分配较多的重建资源。

2.2.1 判断分组

图像块的标准差代表像素在块内的交流功率，可以反映图像平滑程度，标准差越小，则图像块中像素差异越小，图像越平滑。在一定程度上，图像块估计值的标准差也可以反映对应图像块的平滑程度。基于此，计算初步重建图像块zinit的样本标准差σi(i=1，2，…，L)和样本标准差的均值。设定阈值，依据阈值对图像块数据进行分组，分为光滑块、非光滑块两组。样本标准差σi和其均值σˉ通过式（2）得到，其中：zi，j为第i个初步重建图像块的第j个像素值，的均值。若满足条件，则该图像块标记为光滑块；若满足条件，则该图像块标记为非光滑块。

2.2.2 分组重建

若图像块被判断为光滑块，则块中像素灰度值相差不大，可以认为该图像块的稀疏度较大，故直接采用该图像块对应的初始重建值作为增强重建值，如式（3）所示。若图像块被判断为非光滑块，则通过非光滑块残差分支学习图像块初始重建图像与原始图像的残差di，nons，该图像块的增强重建值的计算公式如式（4）所示。非光滑块残差分支由3 层卷积、2 个结构特征交互模块、1 个通道注意力模块（Squeeze-And-Excitation）［15］和1 个3×3 卷积组成。3 层卷积层的第1 层有72 个3×3 卷积核，第2 层有40 个3×3 的卷积核，第3 层有16 个卷积核，每一层后面加激活函数ReLU（Rectified Linear Units）［16］。在非光滑块残差分支中，2 个结构特征交互模块进行了一次递归，在保存模型时只需保存一个模块的参数。递归操作是指串联指定模块，模块中对应位置的卷积层之间进行权重共享，进而能在加深网络深度同时不增加参数［17］。最后，将块分组重建支路输出的两组块重建图按顺序拼接，得到该支路的全图重建值Iglout∈RIW×IH。

为了获取和融合丰富的图像结构信息，更好地重建图像的纹理和边缘，构建结构特征交互模块，该模块由结构特征提取和特征融合两部分组成，如图2 所示。模块输入数据用表示，c为输入数据的通道数，先对输入数据v提取结构特征。结构特征提取部分由5 条并行支路和1 个级联操作（concatenate）［12］组成。5 条并行支路的通道数均为c，第1 条支路采用1×1 的卷积核，第2～5 条支路分别采用空洞率为1、4、6、8 的3×3 空洞卷积［18］。使用级联操作聚合5 条并行支路输出的不同尺度特征，得到聚合特征。另外，为使输出的特征图尺寸与输入的特征图尺寸相同，令结构特征交互模块中空洞卷积的步长和空洞率保持一致。特征融合部分通过卷积层和跳跃连接［9］逐步融合特征信息，首先对5c张特征图使用通道注意力模块［15］，使用1×1 卷积将特征图的数量从5c减少到c，得到交互后的特征，再使用直接映射连接结构特征交互模块的输入形成局部残差结构，连接激活函数ReLU 得到特征vres，如式（5）所示：

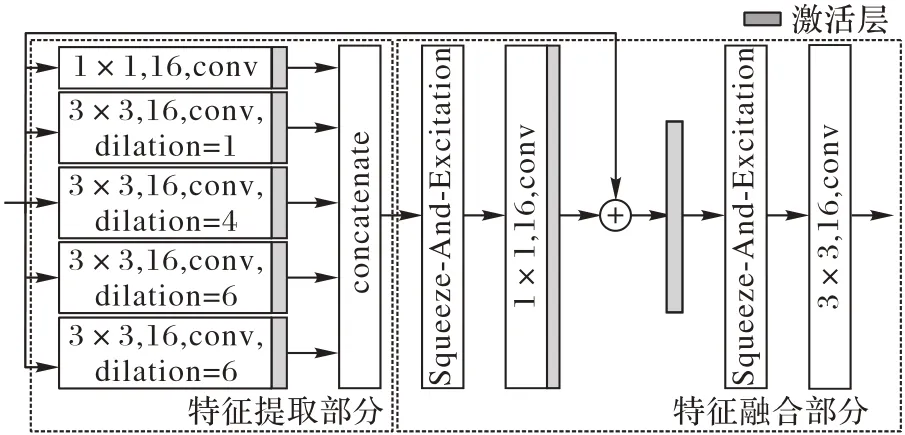
图2 结构特征交互模块Fig.2 Structure feature fusion module

vres通过通道注意力模块和c个3×3 卷积核，以再次进行通道和空间的信息交互，得到结构特征交互模块的输出。结构特征交互模块的输入与输出数据的尺寸一致，可作为网络中即插即用的模块。

2.3 全图重建支路

在由图像块拼接所得的全图中，相邻图像块之间会有一条细长的缝隙，使得边界像素值不连续，这影响了图像的清晰度。在低采样率情况下，重建图像块边界处的像素值跳变更明显。块边界像素值产生跳变的原因是分块压缩感知框架中对全图进行了非重叠分块处理，并独立地进行压缩观测和重建，这减弱了原始图像块的像素在空间上的相关性。图像分块后各图像块的稀疏度不一样，稀疏度大的图像块重建质量好，稀疏度小的图像块重建质量较差，不同重建效果的图像块合成一幅全图时，块与块衔接处的亮度呈伪周期突变。观察多个图像会发现图像像素间具有很强的自相关性，空间邻近的像素灰度值连续性较大，故考虑在支路中利用相邻图像块之间的空域相关性，对相邻图像块之间的像素进行信息交互。双边滤波［19］属于空域上的滤波，能够将图像的空间信息与像素值结合在一起，使得图像块与图像块之间的像素值更连续，并在融合图像像素的同时保持图像的边缘结构特征。与池化和上采样的联合操作相比，空洞卷积操作能在不损失精度的同时获得较大的感受野；与大尺寸卷积核相比，参数量更少。因此全局重建支路中，加入了双边滤波操作和空洞卷积操作，以获得相邻图像块像素间的多种信息交互。

全图重建支路包括全图拼接和全图重建两部分。全图拼接将线性映射的输出按照分块顺序进行逐块拼接，得到全图初始重建图像Iinit∈R1×1×IW×IH。全图重建部分对全图初始重建图像Iinit进行增强重建。首先将Iinit输入两并行分支：一条分支包括一次双边滤波操作和两层卷积层，另一条分支包括两层卷积层，第一层和第二层都有16个3×3 的卷积核，每一层卷积层后面加ReLU 激活函数；然后，将两分支的输出使用级联操作合成32 张特征图，把级联后的32 张特征图送入1×1 卷积层，进行跨通道交互得到浅层特征Isf∈R1×16×IW×IH，再将Isf送入结构特征交互模块，得到信息交互后的全图特征Idff∈R1×16×IW×IH；最后，通过3×3 卷积得到全图重建支路输出值Igout∈RIW×IH。为了减少参数值，全图重建部分两分支中对应的两层3×3的卷积层间共享参数。

2.4 支路加权策略

支路加权融合使用了像素融合方式，操作简单，融合速度快，同时设置非固定的权值用于进行两分支图像的融合。不同采样率情况下的两支路所得图像输出重要性不一致。在低采样率的情况下，观测值中所含信息少，且各块之间的重建独立，故块分组重建支路的拼接所得全图中易出现不同程度的伪周期的像素跳变，而这时全图重建支路融合了图像的空间位置信息，所得输出更接近原始全图。为降低融合图像块边界像素间跳变程度，全图重建支路的输出应具有更大权值。相反地，在采样率较高的情况下，观测值中所包含的图像信息较多，应更侧重于块分组重建支路的重建，该支路的输出应具有更大权值，若此时分配给全图重建支路的输出以大权值，由于全图重建支路中的双边滤波操作将对图像进行平滑处理，反而会使得图像重建精度降低。

因此，采用自适应的加权融合策略，使得不同采样率下的图像融合都有较好的重建效果。对块分组重建支路输出Iglout与全图重建支路输出Igout进行加权平均得到网络最终重建全图I∗，如式（6）所示：

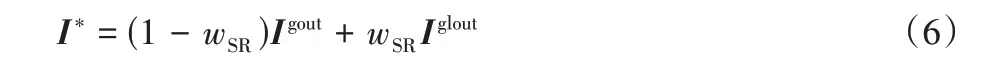
式中：wSR为自适应权值，且有wSR=w×SR，SR为采样率（sampling rate），SR=m/B，w为自适应加权参数。图像的采样率SR在(0，0.5]内取值，因此w的取值范围为(1，2]，在w取中间值时，各采样率下两支路输出图像的融合效果均较好，本文中w取1.6。

3 网络训练

本文以自然图像数据为重建对象，训练集共有291 张图像，采用公开的T91（Timeofte dataset）数据集［10］和BSD200-train（Berkeley Segmentation Datasets）数据集［20］中的图像作为训练数据。BSD200-train 数据集是伯克利大学计算机视觉团队提供的BSD500 中的训练集。将训练集中的图像从RGB颜色空间变换到YCrCb 颜色空间，并对图像依次不重叠地从左到右和从上到下进行滑动取块，所得图像块大小为16×16，这些图像块的亮度分量构成了训练集的标签。若图像的行值和列值不能整除，则在图像的右边和下边补零，使得补零后的图像能刚好在滑动取块时被完整分割完。将16×16的图像块拉为256×1 维的向量，并归一化到[0，1]。所有的块向量组成图像矩阵X，使用随机高斯矩阵作为观测矩阵Φ对图像块矩阵X进行采样，得到观测值矩阵Y。本文采用5种不同的采样率对图像块进行采样，分别是0.01、0.04、0.05、0.10、0.15。每一个图像块有256 个像素，所以对应观测值yi中的测量数m分别是3、11、13、26、38。所使用的损失函数为均方误差，具体损失函数如式（7）所示：

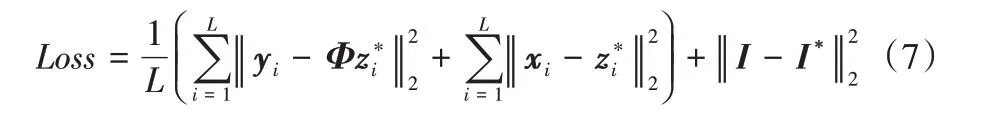
其中：代表块分组重建支路中第i个图像块的重建值，I代表原始图像，I∗代表网络的最终重建图。

训练和测试的操作系统为Windows 10 系统，图形处理器（Graphics Processing Unit，GPU）型号为GTX1080Ti。使用Python3.6 和Pytorch 深度学习开源框架训练，训练过程的优化器选用 Adam［21］。采用Pytorch 框架中的ReduceLROnPlateau 方法自适应调整学习率，初始学习率为0.001，当损失值超过30 个epoch 后不下降时，学习率衰减为原来的1/10，当学习率低至1×10-6时，学习率不再变化，最大迭代周期为500 epoch。通过自适应调整学习率，网络在加速收敛的同时能提高重建精度。在网络参数的初始化方面，全连接层使用均值为0、方差为1 的高斯矩阵作为初始化权重，所有卷积采用Pytorch 框架中默认的He_uniform 均匀分布［22］初始化方式。

训练完成后采用压缩感知领域常用的6 幅测试图像［10］和标准测试数据集Set11［12］进行测试。实验中的6 幅测试图像如图3 所示。

图3 实验中采用的6张测试图像Fig.3 Six test images used in experiments

4 实验及分析

4.1 不同方法间的重建性能对比

为了具体分析本文方法的重建性能，将提出的重建方法与已有的六种方法进行比较，包括基于增广拉格朗日乘子的全变分正则化方法TVAL3（Total Variation Augmented Lagrangian ALternating-direction ALgorithm）［23］、基于去噪的近似消息传递（Denoising-based Approximate Message Passing，D-AMP）法［24］两种基于迭代优化的传统压缩感知图像重建方法，以及基于深度学习的神经网络ReconNet、NL-MRN、DR2-Net 和MSRNet。TVAL3、D-AMP、ReconNet 和NL-MRN 使用文献［10］提供的结果，DR2-Net 和MSRNet 使用文献［12］提供的结果。实验从主观视觉效果和重建图像的图像质量量化指标两方面对不同重建方法的重建性能进行比较分析。图像质量量化指标选用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）和结构相似度（Structural SIMilarity index，SSIM）。

1）重建图像主观视觉效果比较。

本文方法与TVAL3、D-AMP、ReconNet 和NL-MRN 这四种方法的重建图像视觉效果比较如图4、5 所示，分别选择了Boats 图和House 图作为测试重建图。

图4 是采样率为0.10 时各方法对图像Boats 的重建对比，Boats 图细节纹理丰富。从图4 中的重建图像以及它们的图像的局部放大图的对比可以看出，本文方法获得的重建图像与对比方法的重建图像相比较，重建图像有更丰富的细节，能够较好地保持原图的整体结构。在Boats 图的局部放大图像中，远处船体的桅杆重建得更清晰，相邻图像分块边界像素值也更趋于相同。

图5 是在采样率为0.05 时的不同重建方法对图像House重建对比，House 图中的纹理区和光滑区分割明显。在图5（b）～（d）的局部放大的图像中可以观察到，图像相邻块中有深浅不一的格状痕迹，相邻的图像块之间有一条细长的缝隙，使得边界不连续。图5（e）中对应的重建的图像为本文方法所重建的图像，可以看出图像中没有明显的格状痕迹，光滑区域更平滑，边缘和曲线结构更连贯。从图4 和图5 中可以看出，本文方法的重建图像具有更优的视觉效果。

图4 采样率为0.10时不同方法重建结果对比Fig.4 Reconstruction result comparison of different methods with sampling rate of 0.10

图5 采样率为0.05时不同方法重建结果对比Fig.5 Reconstruction result comparison of different methods with sampling rate of 0.05

2）图像质量量化指标比较。

为了更客观地将本文方法与其他方法相比较，给出了图3 中6 张测试重建图像不同采样率对应的PSNR 折线图和SSIM 折线图，如图6、7 所示；同时给出了不同方法在不同数据集下具体的PSNR 均值和SSIM 均值，如表1 和表2 所示，最好的结果以粗体突出显示。

图6 不同采样率下各方法的6张测试图像的PSNR折线图Fig.6 PSNR line charts of 6 test images of each method at different sampling rates

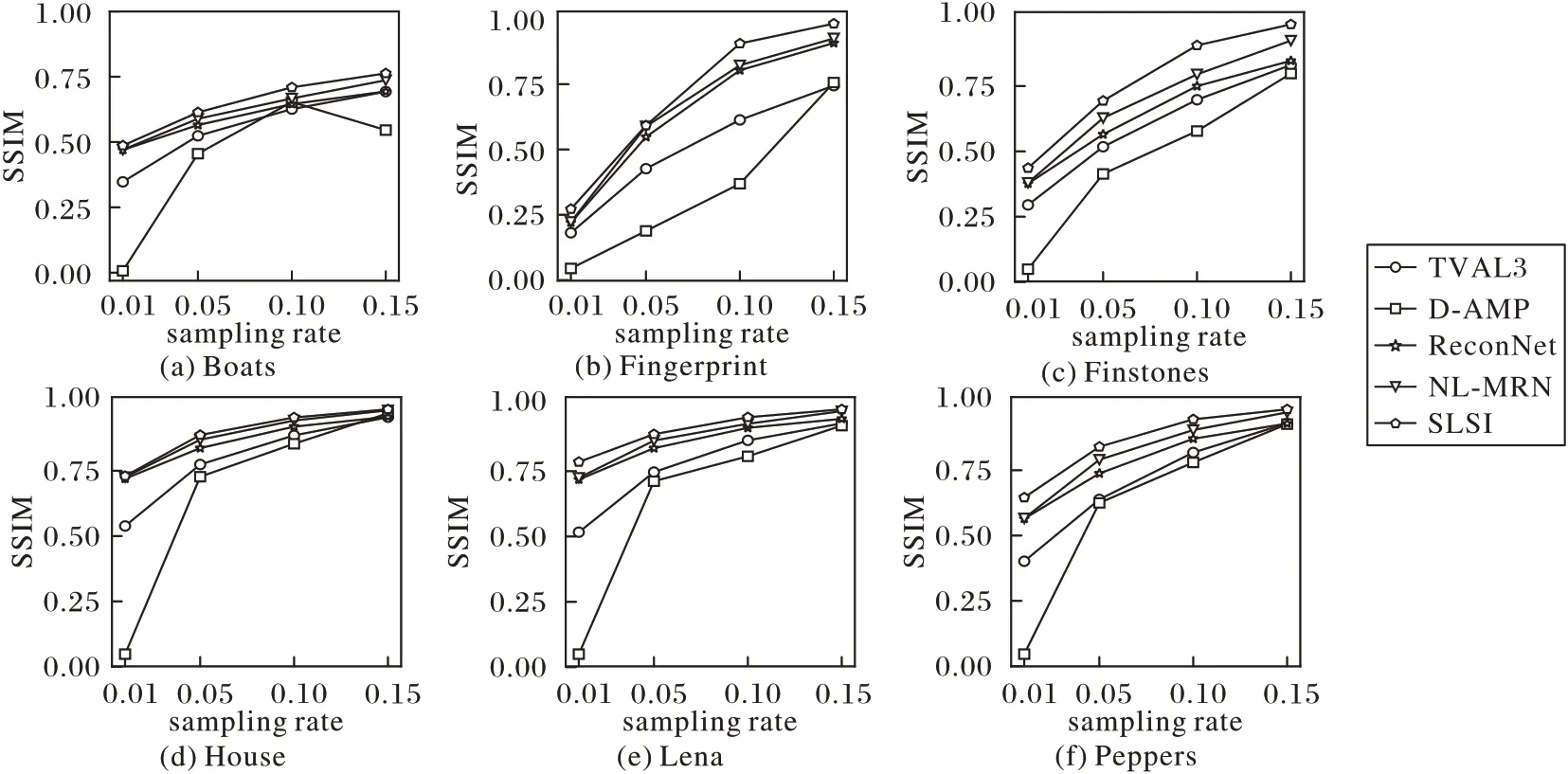
图7 不同采样率下各方法的6张测试图像的SSIM折线图Fig.7 SSIM line charts of 6 test images of each method at different sampling rates

表1 各方法在6张测试图像上的PSNR均值和SSIM均值Tab.1 Comparison of average PSNR and average SSIM among different methods on 6 test images

在图6、7 中，不同方法所对应的重建图像的PSNR值和SSIM值由折线图的形式展示，横坐标为采样率。重建图像PSNR值和SSIM值越高，则代表图像重建质量越高。可以发现本文方法在各个采样率下都在对比方法对应的折线之上，这表明在本文方法在各个采样率所对应的图像重建值均比对比方法的高。从图6、7 中可以发现，采样率越低，重建图像对应PSNR值和SSIM值越低，这是因为采样率越低，观测数据也将减少，所用于重建的信息也越少。由于本文方法中的全图重建支路融合了相邻图像块间像素的相关性，相当于增加了可用重建信息，因此能在低采样率的情况下得到比其他方法更高的PSNR值和SSIM值。

表1 展示了不同方法在图3 中的6 张测试图对应所得重建图PSNR 均值和SSIM 均值。由表1 可知，本文方法在4 种采样率下的重建图像的PSNR 均值和SSIM 均值高于传统的基于迭代的TVAL3 和D-AMP 方法，也高于目前的基于深度学习的ReconNet、NL-MRN 方法，如在采样率为0.05 的情况下，所提方法对应的PSNR 均值和SSIM 均值在图3 所示图像上分别平均提升了2.617 5 dB 和0.105 3。

表2 展示了不同方法在标准测试数据集Set11 下所得重建图的SSIM值。

表2 各方法在Set11数据集上的平均SSIMTab.2 Comparison of average SSIM of different methods on Set11 dataset

由表2 可知，本文方法在3 种采样率下的重建图像SSIM值均高于对比方法。表1 和表2 的结果证明了本文方法在提升图像重建质量方面的有效性。

4.2 消融实验分析

为了探究各支路对本文方法的影响，分别设计两个网络SLSI-gl 和SLSI-g 进行消融实验。以块分组重建支路为主，移除SLSI 网络中的全图重建支路，从而构成网络SLSI-gl。相对应地，以全图重建支路为主，移除SLSI 网络中的块分组重建支路，从而构成网络SLSI-g。对SLSI-gl、SLSI-g、SLSI 这三个网络使用相同的训练策略进行模型训练，并用图3 所示的6 幅测试图像进行重建测试，实验结果如图8～9 所示。

图8 对应采样率为0.01 时三个网络在500 次迭代中的训练结果。横坐标为迭代次数，纵坐标为6 张测试图像对应的PSNR 均值，曲线代表了PSNR 均值随迭代次数增长的变化情况。

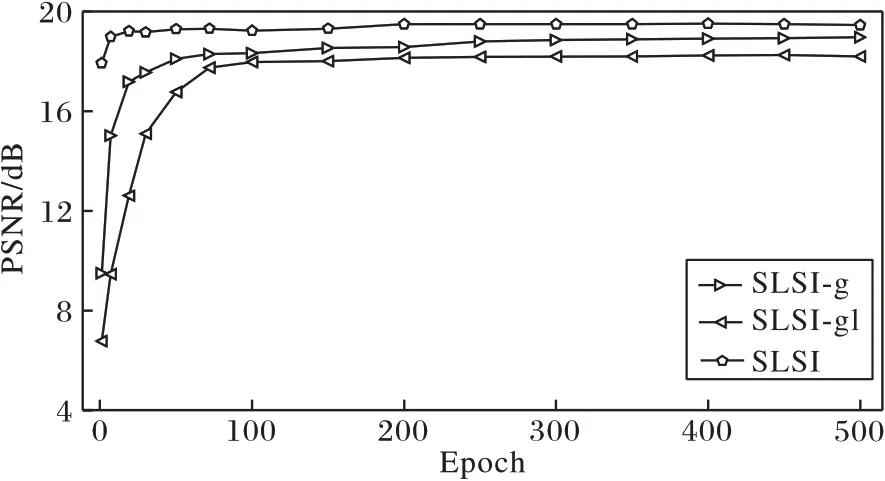
图8 消融实验在采样率为0.01下的训练结果Fig.8 Training results of ablation experiment at sampling rate of 0.01

观察图8 中的曲线变化，分析三个网络的收敛情况。当迭代次数较小时，随迭代次数增加，网络对应的PSNR 均值逐步提升，这表明该网络逐渐收敛。然后，网络对应的曲线趋向水平，这表明训练过程逐渐稳定，达到收敛状态。从图8 中的三条曲线对比可以看到，SLSI 所对应的带五边形符号标记的实折线最先达到水平状态，SLSI-g、SLSI-gl 次之，这表明网络SLSI 的训练收敛速度最快。另外，当三个网络训练收敛后，SLSI 网络对应的PSNR 均值最高。结合块分组重建支路和全图重建支路的网络，和仅使用一条支路相比，在收敛速度和训练性能上的结果更优。

图9 展示了原图和采样率为0.01 下SLSI-gl、SLSI-g、SLSI网络对应的Peppers 重建图像。图9（b）中图像块的像素值趋向于统一，较难分辨出图像的曲线边缘；图9（c）上能看到图像的大致轮廓，但图像中有较多的白点；图9（d）中图像的重建轮廓最清晰。通过图9（b）～（d）的重建图与图9（a）的原图进行对比，可以发现图9（d）的重建效果最好。

通过消融实验可以发现：在同等条件下，移除了两支路中的任一条支路，都会使得重建网络的重建精度降低，图像重建视觉效果变差。SLSI 的图像重建效果最优，一方面是融合两支路增加了网络参数，网络拟合能力更强；另一方面是块分组重建支路和全图重建支路所得结果可以进行互补，进而提高了整体的重建效果。

综上，SLSI 能够有效地重建出图像的细节，减少低采样率下重建图像的空间位置信息丢失，相比TVAL3、D-AMP、ReconNet、NL-MRN、DR2-Net、MSRNet 这6 种方法，能够获得更高的PSNR值和SSIM值，更好的视觉效果。

5 结语

本文提出了一种在分块压缩感知框架下融合空间位置与图像结构信息的压缩感知图像重建方法。一方面为稀疏度不同的块设置不同的增强重建策略以降低计算量，另一方面在重建过程中建立了分块图像间的位置联系，在一定程度上弥补了由分块采样带来的空间位置信息损失。实验结果表明，在低采样率的情况下，相较于常规的图像分块重建方法，所提方法对应的重建图像的视觉效果更好，所得PSNR值和SSIM值更高。本文方法在低采样率下也能通过少数观测值恢复图像的轮廓，适用于资源受限且目标是对图像的高层次理解的场景。