基于金融技术指标的用电数据分析

2022-04-12蒋群孙钢殷杰刘英

计算机应用 2022年3期

杨安，蒋群，孙钢，殷杰，刘英*

（1.浙江大学信息与电子工程学院，杭州 310027；2.国网浙江省电力有限公司营销服务中心，杭州 311121；3.浙江华云信息科技有限公司，杭州 310012）

0 引言

当前，智能电网建设正推动着大数据与电力应用的结合。电力大数据分析不仅能够及时、准确地掌握用户用电行为特征，而且能够从电力角度评估企业发展的活力，进一步调整供电政策、改善电力配置、提高经济效益，为电力行业运营和服务优化奠定必要基础［1-2］。

异动分析和负荷预测是电力大数据分析中两项重要研究内容。在异动分析方面，阈值检测是最简单可行的方案。例如，文献［3］中通过分析异动的深层原因，利用专家知识设置阈值准则有效捕捉了由窃电引起的异动。从数据分析角度出发，文献［4］中利用高斯核密度估计法寻找最优阈值，在路灯窃电检测中有较好表现。除阈值检测法外，聚类、局部离群因子等机器学习方法也被广泛应用于电力异动分析领域。文献［5］中使用基于密度和网格的局部离群因子算法挖掘异常用电模式；文献［6-8］中则利用不同的聚类算法刻画异动或非异动的用电行为模式，并在此基础上使用局部离群因子、关联分析、朴素贝叶斯分类、聚类等实现异动检测。

在负荷预测方面，早期研究通常采用差分整合移动平均自回归（AutoRegressive Integrated Moving Average，ARIMA）［9-10］、Prophet［11-12］等时序预测模型对负荷数据进行预测。随着人工智能的发展，神经网络受到了越来越多的关注。文献［13-14］中分别使用猫群优化算法和粒子群优化算法优化后向传播（Back Propagation，BP）神经网络，提高了负荷预测的稳定性；文献［15］中通过构建多尺度长短期记忆（Long Short-Term Memory，LSTM）网络模型捕捉多尺度特征以提高预测精度；文献［16-17］中使用卷积神经网络（Convolutional Neural Network，CNN）与循环神经网络（Recurrent Neural Network，RNN）模型组合设计，融合局部特征与时序特征提高了预测模型的性能。

然而，目前异动分析与负荷预测的大多数算法依赖于专家知识，例如异动原因的深层剖析、机器学习算法的特殊组合设计、模型超参数的确定等。这是因为已有算法通常采用平均负荷率、日峰谷差率、平期负载率、最大最小负荷等传统负荷特征作为异动分析与负荷预测的数据特征，而这些特征难以全面表征负荷时间序列，严重影响了模型的精度。与此同时，绝大多数已有算法还通常需要加入辅助信息，例如天气、温湿度等，增加了不必要的成本。

鉴于用电负荷数据与金融股票数据具有相似的数据特征表示，本文适应性地将某些金融技术指标迁移至用电负荷时间序列的描述中，开展了用电数据分析，降低了对专家知识、特殊设计的算法模型结构和辅助信息的依赖性，主要工作如下：1）将金融技术指标适应性地引入到用电时间序列分析中，分析了金融技术指标在刻画用电时间序列特征方面的有效性；2）采用统计方法对各项金融技术指标进行统计分析，并采用阈值检测识别异常用电情况；3）提取与金融相关的日负荷指标特征，构建了LSTM 负荷预测模型。

1 技术指标

类比于股票分析中通常采用股票价格时间序列为研究对象，本文对日平均负荷曲线进行分析，并计算相关的金融技术指标以刻画用户用电数据特征。

1.1 十字过滤线指标

在金融领域，十字过滤线（Vertical Horizontal Filter，VHF）指标用于行情定位，即分辨趋势行情或震荡行情。趋势行情表示时序数据呈现宏观趋势走向，而震荡行情表示时序数据在某水平附近波动，无明显的涨跌趋势。本文使用VHF 指标捕捉用电数据的趋势走向，其计算方式如式（1）所示：

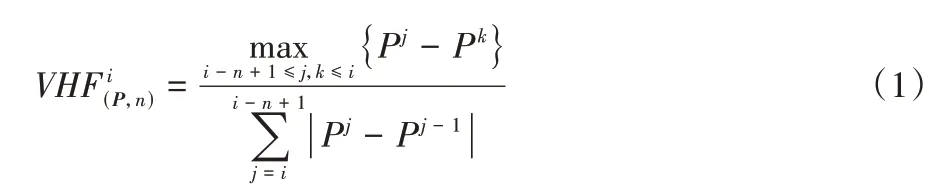
其中：P=[Pi]表示日平均负荷序列,表示序列P的n日VHF 指标序列，上标i表示第i日。VHF 取值范围为[0，1]，数值越大，意味着所考察时刻的前n日日平均负荷时序数据趋势性越强；反之，VHF 指标值越小，则意味着前n日日平均负荷时序数据呈震荡变动。鉴于用电日平均负荷波动具备一定的社会生产周期性，同时参考金融数据分析，本文选取VHF 指标参数n=28，用以表征以月为时间跨度的负荷数据的趋势性。

图1 给出了杭州市某企业用户从2018 年1 月到12 月的日平均负荷曲线及对应的VHF 指标曲线。从图1 中可以看出，在2～3 月份以及11 月份负荷序列趋势较强的位置，对应的VHF 数值较高，而在VHF 数值较低的5 月份到10 月份，日平均负荷序列表现为震荡，无明显趋势变动。

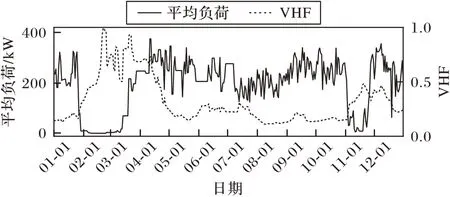
图1 2018年杭州市某企业日平均负荷曲线及对应VHFFig.1 Daily average load curve and corresponding VHF of a company in Hangzhou City in 2018

1.2 异同移动平均线指标

在金融市场中，异同移动平均线（Moving Average Convergence/Divergence，MACD）指标［18］被称为指标之王，用于描述价格变化的趋势强度与方向。MACD 可通过计算快速指数移动平均线（Exponential Moving Average，EMA）与慢速指数移动平均线之间的差值再经平滑后得到。当MACD从负到正，即快速均线超越慢速均线，意味着当前处于上升趋势；反之，则处于下降趋势。MACD 具有移动平均线共同的滞后性，而趋势滞后性不利于负荷预测或异动捕捉。针对上述不足，本文采用零滞后异同移动平均线（Zero Lag Moving Average Convergence/Divergence，ZLMACD）指标刻画电力数据特征，从而及时捕捉电力数据的趋势强度和方向，其计算方式如式（2）～（5）所示：

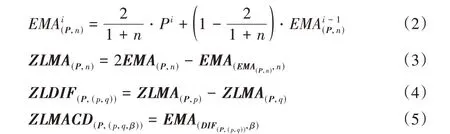
图2 给出了杭州市某企业用户2018 年1～6 月份的日平均负荷曲线及对应的MACD 指标曲线。从图2 中可以看出，日平均负荷序列呈上升趋势时，ZLMACD 指标为正；反之，日平均负荷序列呈下降趋势时，ZLMACD 指标为负。需注意的是，在反映负荷趋势变动时，ZLMACD 指标穿越0 轴均领先MACD 指标，表明滞后性有所改善，滞后性的改善有益于及时捕捉用电数据的趋势特征。

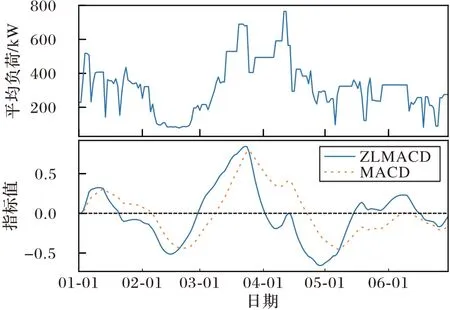
图2 2018年上半年杭州市某企业日平均负荷曲线及对应MACDFig.2 Daily average load curve and corresponding MACD of a company in Hangzhou City in first half of 2018

1.3 布林线指标

布林线（BOLLinger band，BOLL）指标基于标准差原理为时序数据波动划定信赖区间，该区间由中轨线、上轨线和下轨线共同构成［19］。在金融分析中，中轨线常使用成本线构建。用电数据分析任务中无成本概念，故本文考虑使用移动平均线（Moving Average，MA）构建中轨线，反映用电负荷的稳定状态。移动平均线目的是消除原序列的干扰因素，平滑原序列，以此保留本质内容。均线一般都具有滞后性，常落后于原时间序列的趋势变化，更平滑意味着滞后性也更明显。BOLL 指标所用均线应尽可能保证低滞后，故本文使用最小二乘移动平均线（Least Square Moving Average，LSMA）作为中轨线。LSMA 是基于最小二乘法的思想使用直线拟合过去n日的数据，并将当日拟合数据点作为当日均值。相较于普通移动平均线MA，LSMA 可改善滞后现象，在滞后性和稳定性之间获得较好权衡。

图3 给出了杭州市某企业2018 年全年日平均负荷曲线的普通移动平均线MA（14）和最小二乘移动平均线LSMA（14），其中括号内参数“14”表示14 日的移动平均。从图3 可以发现，LSMA（14）在保证较好平滑性的同时，相较于MA（14）具有更低的时滞。

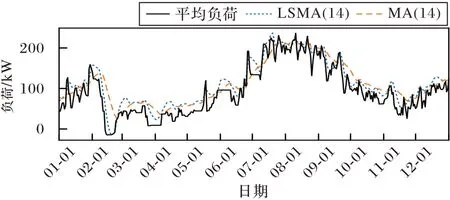
图3 2018年杭州市某企业日平均负荷曲线及对应MA和LSMAFig.3 Daily average load curve and corresponding MA and LSMA of a company in Hangzhou City in 2018

基于LSMA 构建中轨线，BOLL 指标计算方式如式（6）～（8）所示：

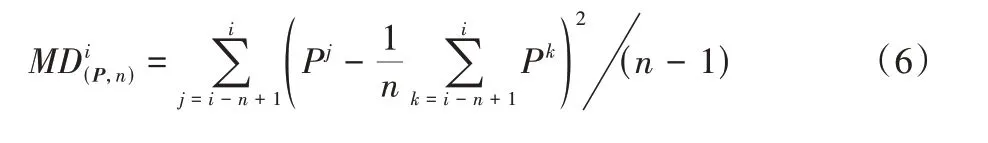
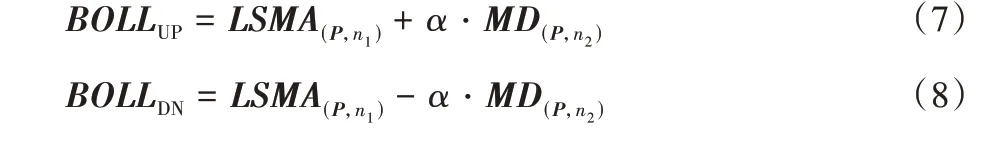
图4 给出了杭州市某企业用户2018 年上半年1～6 月的日平均负荷曲线及其对应的布林线指标。图4 中1～2 月份和5～6 月份有箭头指示的时间序列超出布林线边界，意味着平均负荷序列产生较剧烈的震荡。实验结果表明，布林线指标相较于趋势性指标VHF 和ZLMACD，对突变信号更为敏感。

2 基于金融技术指标的异动分析

用电异动通常可以反映在负荷的趋势变动中，金融技术指标能够有效地捕捉用电趋势变化，有助于寻找企业异动行为。本文提出基于金融技术指标的异动分析算法，该算法包含数据预处理、技术指标阈值选取、指标联合异动分析三部分。选取杭州市工业用户作为考察对象，考察时间范围从2018 年1 月1 日到2018 年12 月31 日共计365 日，数据选取每日平均负荷值，记日平均负荷序列为Praw。

2.1 数据预处理

为了使所有用户在指标数值上具有可比性，在计算指标前需对各个用户的日平均负荷序列数据进行标准化处理，即

其中：μP指日平均负荷均值，σP指日平均负荷标准差。

2.2 技术指标阈值选取

直观上，同一行业内用户个体间用电趋势具有潜在的一致性，因此本文根据行业确立阈值，即技术指标的阈值在同一行业范围内确定。图5 给出了杭州市所有工业用户2018年全年的VHF 和ZLMACD 指标数值统计结果。VHF 指标表征趋势性强度，指标值越接近1 表示趋势性越强，通常越接近1 的概率也越小；同时，ZLMACD 指标表征趋势变动情况，取值有正有负，指标绝对值越大表明上升或者下降趋势越强，通常绝对值越大则概率越小。

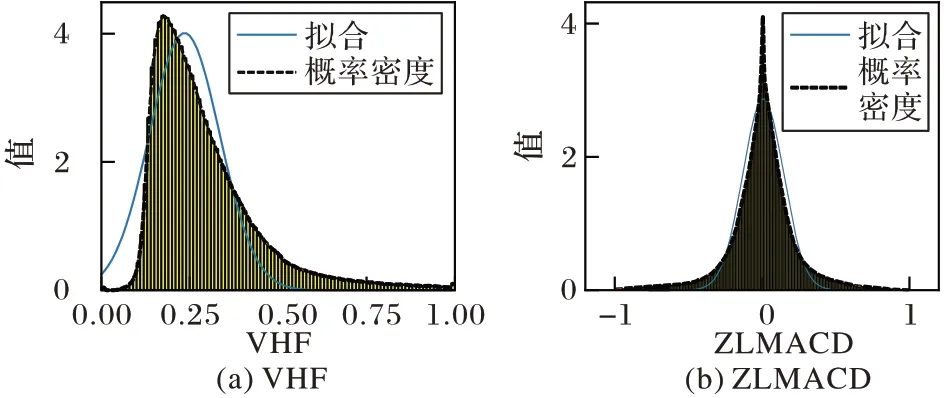
图5 2018年杭州市所有工业用户VHF和ZLMACD数值统计图Fig.5 Numerical statistics of VHF and ZLMACD of all the industry users in Hangzhou City in 2018

根据图5 正态拟合曲线可知，VHF 和ZLMACD 这两个指标都接近于正态分布，因而本文利用偏度系数和峰度系数衡量数据分布，进而确定异动判断的阈值。偏度系数skew和峰度系数kurt计算方式如式（10）～（11）所示：

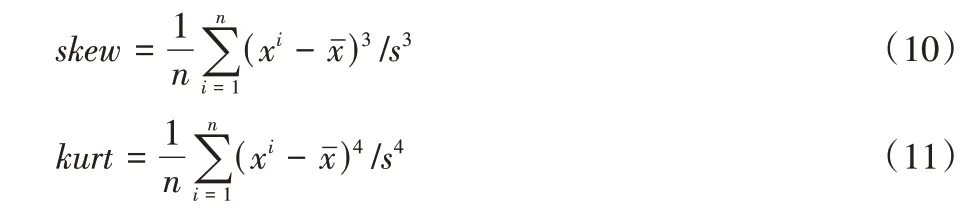
其中：和s分别表示VHF 或ZLMACD 序列的平均值和标准差。偏度系数skew度量数据分布的对称性，而峰度系数kurt则度量数据分布的峰高程度。在标准正态分布中，偏度系数与峰度系数均为0。

通过考察偏度系数与峰度系数，本文在VHF 指标分布后尾处选择阈值，选取二倍均值与95%分位数中的较大者作为阈值。根据ZLMACD 指标近似正态分布的特性，分别选取三倍标准差之外且绝对值不小于2.5%分位数和97.5%分位数作为双边阈值。经统计分析，杭州市工业用户可选VHF指标阈值为0.59，ZLMACD 指标阈值为-0.52 和0.49。本文在不同行业的实验结果表明，不同行业VHF 与ZLMACD 指标分布基本相似，在选择指标阈值可采取同样的策略。

2.3 联合VHF和ZLMACD的异动分析

ZLMACD 指标作为趋势性指标，在震荡行情时将频繁波动，只采用该指标作异动分析将产生虚警。VHF 指标指示是否处于趋势行情，反映局部时间范围的趋势变动情况，对于任何可疑用电趋势变动都有较好的警示，相当于为ZLMACD指标预警提供置信度。为了提高异动检测的准确率，本文将综合考虑VHF 和ZLMACD 两个指标超出阈值的情况进行异动分析。

图6 给出了联合VHF 与ZLMACD 后杭州市某一用户异动分析结果，其中被着色部分是超出指标阈值的部分。实验结果表明VHF 与ZLMACD 指标在2～3 月份和8～9 月份均有超出阈值部分，其对应的用电时间序列也有直观上不正常的趋势变动，两者结论一致。

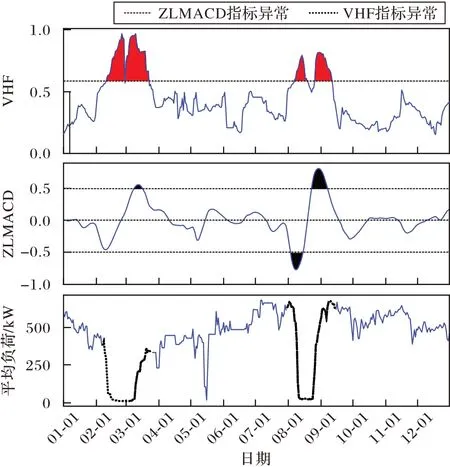
图6 某工业用户联合VHF和ZLMACD的异动分析结果Fig.6 Results of anomaly detection of an industry user by combining VHF and ZLMACD

3 基于金融技术指标的负荷预测

负荷预测旨在依赖给定的负荷数据预测未来负荷值，预测的关键在于对趋势的把握。金融技术指标能够更好地捕捉负荷趋势特征信息，将其作为特征加入至机器学习模型中有助于实现更为精准的预测。本文提出了基于金融技术指标的负荷预测算法LSTM-FI（Long Shot-Term Memory network with Financial Indicators），该算法包含数据预处理、负荷特征选取、负荷预测及结果分析三部分。实验数据为杭州市工业用户每日96 点负荷数据，考察时间范围从2018 年8 月26 日至2018 年11 月28 日。

3.1 数据预处理

在金融二级市场中，价格市场的变动常使用K 线图作为分析工具。K 线图由开盘价、收盘价、最高价、最低价共四项指标构建，相较于若干曲线的表现形式，K 线图更为直观，可以展现更多用户负荷信息。因而，本文使用K 线图描述用户用电负荷变动并基于K 线图构建预测模型。参考文献［20］，在对负荷数据采取标准化处理之后，使用日最大负荷Pmax、日最小负荷Pmin、日尖峰平均负荷Ppeak_avg、日平谷平均负荷Ptrough_avg四项核心参数构建负荷K 线图。杭州市工业用电分时划分为：尖峰时段19：00—21：00；高峰时段8：00—11：00、13：00—19：00、21：00—22：00；低谷时段11：00—13：00、22：00—次日8：00。本文将日尖峰平均负荷定义为尖峰时段与高峰时段平均负荷，日平谷平均负荷定义为低谷时段平均负荷，K 线实体中心位置为日平均负荷。根据日尖峰平均负荷与日平谷平均负荷之间相对大小关系，负荷K 线存在两种表示形式，如图7 所示。

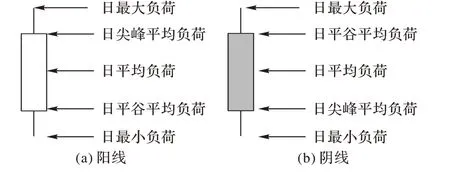
图7 电力负荷K线图Fig.7 Candlestick chart of power load

3.2 负荷特征选取

除K 线核心参数外，本文还采用传统日负荷特性指标，包括日平均负荷率ρavg、日最小负荷率ρmin、日峰谷差Δ等描绘用户用电日负荷特征，计算方式如式（12）～（14）所示：

根据式（12）～（14）可知，传统负荷特性指标是负荷K 线核心参数的非线性组合，这类特征对具备较强非线性表征能力的机器学习模型冗余。金融技术指标能够更好地捕捉负荷趋势特征信息，为传统负荷特性指标提供了补充，有利于提高负荷预测的精度。因此，本文将金融技术指标加入到日负荷特征向量中，构建如表1 所示的14 维日负荷特征向量。

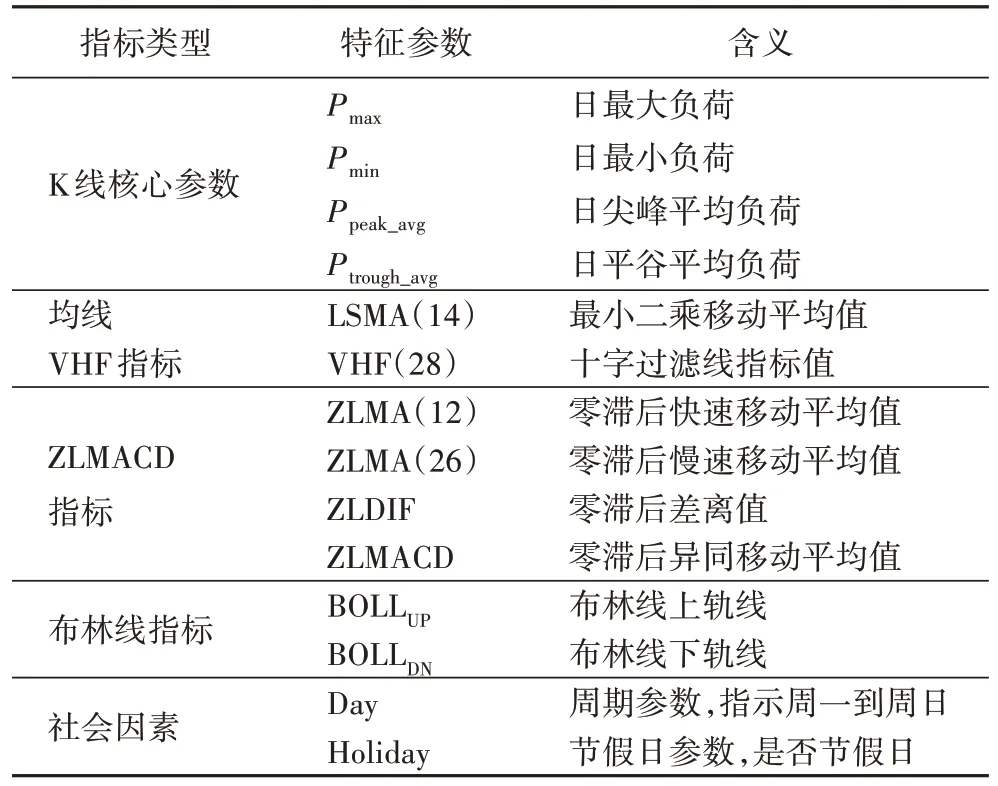
表1 14维日负荷特征向量Tab.1 14-dimensional daily load feature vector

在表1 中，括号中数字表示指标计算中所采用的参数值。除金融技术指标外，14 维日负荷特征向量中还包括两项社会因素指标，包含指示周一到周日的周期参数Day 以及节假日参数Holiday。这两项参数为非定量指标，需对其进行量化处理，Day 取值为{1，2，3，4，5，6，7}分别表示周一到周日，Holiday 取值为{0，1}表示是否为节假日。

3.3 负荷预测及结果分析

RNN 在处理序列化数据时具有独特的优势，其中LSTM是最常见的循环神经网络之一，LSTM 基本单元如图8 所示。

图8 LSTM基本单元结构示意图Fig.8 Schematic diagram of the structure of LSTM cell

LSTM 基本单元主要由状态循环变量Ct和ht组成，相较于RNN，LSTM 通过引入门结构增强了对长期时间序列的表征学习能力，一定程度上避免梯度爆炸问题。LSTM 引入的三项门结构包括遗忘门ft、输入门it、输出门ot，门结构如式（15）～（17）所示：

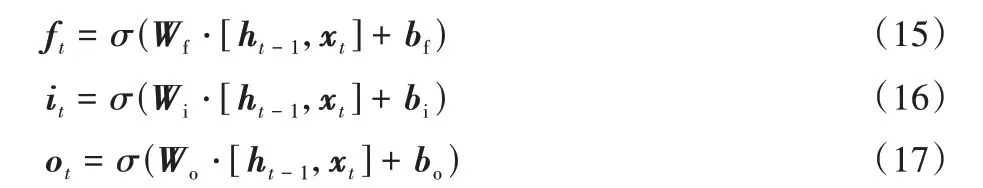
其中：Wf、Wi、Wo表示门结构中的权重矩阵，bf、bi、bo表示偏置向量，[⋅，⋅]表示矩阵向量的拼接组合，σ(⋅)表示sigmoid 激活函数。LSTM 基本单元中状态循环变量Ct和ht的正向推理方程如式（18）～（19）所示：

其中：WC表示更新状态变量的权重矩阵，bC表示偏置向量，“*”表示按元素乘运算。

基于电力K 线图，本文构建基于金融技术指标的LSTMFI 模型。LSTM-FI 模型包含单个LSTM 基本单元和一层全连接层。在每个时刻t，LSTM 基本单元依次读入对应时刻数据xt，通过遗忘门、输入门、输出门等结构选择性地遗忘或记忆序列长短期潜在信息，将最终时刻输出ht作为全连接层的输入，输出4 维向量作为预测的负荷K 线核心参数。LSTM-FI模型基于反向传播训练，整体结构如图9 所示。

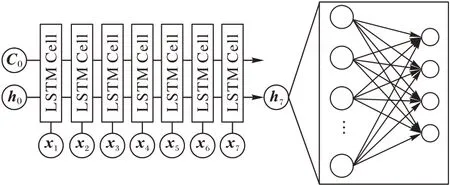
图9 基于金融技术指标的LSTM负荷预测模型示意图Fig.9 Schematic diagram of LSTM load forecasting model based on financial technical indicators

本文采取滑动窗口分割时间序列以构建数据集。设定滑动窗口长度为7，根据表1 构建输入特征向量，则输入维度为7×14，输出维度为1×4。对于任一用户2018 年8 月26 日至2018 年11 月28 日共95 日每日96 点负荷数据，根据滑动窗口共可得89 条数据样本，本文选择前79 日作为训练集，后10 日作为测试集。LSTM-FI 算法负荷K 线图预测结果如图10 所示。

从图10 可以看出，模型预测值与真实值基本一致，表明了LSTM-FI 算法的有效性。

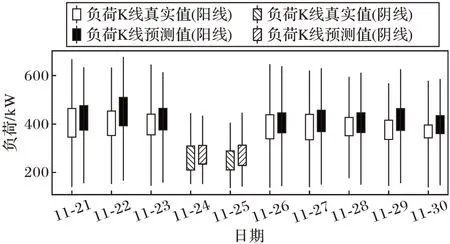
图10 连续10日预测结果K线图Fig.10 Candlestick chart of model prediction results for 10 consecutive days

为了定量评估算法性能，本文采用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）作为预测评价指标，计算方式如式（20）所示：

表2 不同算法的性能比较Tab.2 Performance comparison of different algorithms

实验结果表明，LSTM-FI 算法的平均预测MAPE 为9.272%，优于LSTM-noFI（平均14.746%）、ARIMA（平均11.594%）、Prophet（平均33.447%）和SVM（平均10.582%）。相较于ARIMA、Prophet 和SVM 算法，LSTM-FI 算法将MAPE分别降低了2.322、24.175 和1.310 个百分点。虽然Prophet和SVM 算法的日负荷最小值预测误差小于LSTM-FI 算法，但另外几项K 线图参数预测误差较大。考虑到日负荷最小值缺乏对实际生产的指导意义，综合来看，Prophet 和SVM 算法性能劣于所提预测算法。