基于轨迹点聚类的航路发现方法

刘海杨，孟令航，林仲航，谷源涛

（清华大学电子工程系，北京 100084）

0 引言

通过对海量历史轨迹数据进行深度挖掘，发现未掌握的飞行器航路，进而掌握飞行器的运动规律，是统筹规划全局空域交通管制的基础，同时也是异常轨迹预警的关键。

学术界关于航路发现的研究大多是针对浮动车辆的GPS（Global Positioning System）轨迹数据，目前，未搜集到航路发现相关的研究。

基于浮动车辆GPS 轨迹数据的路网提取方法可以分为4类：

1）聚类方法。对轨迹点或线进行聚类，如Edelkamp等［1］、Schroedl等［2］利用K-means算法对轨迹进行聚类，采用样条曲线拟合道路中心线来提取路网；Worrall 等［3］对轨迹点进行聚类，同时考虑方向角因素，链接各个节点提取路网；米春蕾等［4］、王冬等［5］对数据进行网格化后采用聚类方法，通过链接骨架节点或拟合中心线的方式，得到路网几何数据。

2）Delaunay 三角网法。杨伟等［6］、唐炉亮等［7］对轨迹线构建约束三角网来提取路网。

3）基于栅格化和核密度估计的图像处理方法。Shi等［8］、李俊杰等［9］对轨迹数据进行栅格化处理；Biagioni 等［10］采用核密度估计将轨迹数据转换为图像，然后采用图像处理［11］相关手段提取路网。

4）增量合并方法。Zhang 等［12］、Bruntrup 等［13］、Cao 等［14］主要是根据已有路网和新的轨迹数据对路网进行更新。

飞行器飞行轨迹数据与浮动车辆的轨迹数据有着明显差异：浮动车辆均按照现实存在的道路行驶，行驶线路较简单；而飞行器的航路是抽象的，且飞行轨迹较复杂，前述基于浮动车辆GPS 轨迹数据的路网提取研究成果各有优点，但无法充分利用飞行器运动轨迹的特点和解决轨迹采样率不同、高噪声的问题，直接应用于飞行器航路发现时性能不佳。存在的主要问题如下：

1）虽然众多研究成果对“直线”型航路段的提取效果较好，但对于“圆”状航路结构和多分支的交叉路口结构的提取效果欠佳。“圆”状航路结构容易提取为“点”结构，多分支结构中的部分夹角较小的分支容易被合并。

2）点、线聚类方法对采样率和噪声要求比较严格。

3）Delaunay 三角网、栅格化与核密度估计方法提取航路时，道路段呈锯齿状。

4）增量合并方法主要用于对航路的更新，而且对噪声敏感。

因此，本文设计了一种基于轨迹点聚类的航路发现方法，旨在解决飞行器轨迹数据采样率不同、高噪声问题的同时，改善对特殊航路结构的提取效果。

1 技术路线与主要方法

本文设计了一种抗噪鲁棒、易于实现的基于聚类的航路数据提取方法，具体步骤为：

1）对轨迹数据进行预处理，包括离群点剔除和卡尔曼滤波；

2）对预处理后的轨迹数据进行重采样，使轨迹数据的采样密度基本一致；

3）对轨迹数据点进行聚类，得到航路节点（聚类中心）；

4）对航路节点进行修正，降低航路节点的冗余度；

5）根据轨迹数据点的连接关系，将航路节点进行连接，形成航路几何数据。

1.1 轨迹预处理

本文涉及的轨迹数据由大量离散轨迹数据点组成，并存储在数据库中。轨迹数据点包括轨迹序号、经度、纬度、时间4 项有效属性。由于各种因素的影响，在数据库中存储的轨迹数据存在噪声和离群点，导致数据无法直接使用。针对轨迹数据中存在的噪声和离群点，本文提出了如下解决方案。

1.1.1 离群点剔除

采用一种自适应阈值法对离群点进行剔除操作。由经度、纬度和时间计算轨迹点的平均速度，采用基于数理统计中的3σ 原则，对平均速度大于阈值的轨迹点进行剔除。

1）阈值初始化。根据式（1）计算出整条轨迹各个采样点的平均速度。由于中值对噪声不敏感，所以本文以平均速度的中值乘以一个增益系数η来初始化阈值。

式中：vi是pi点的速度，E0为初始化阈值，(xi，yi)为轨迹中第i个轨迹点pi的坐标，ti为轨迹点pi对应的时间。

2）由于当前轨迹点的运动状态与相邻轨迹点的运动状态有一定的相关性，本文采用滑窗法对整条轨迹的采样点进行判断和剔除。该部分分为两阶段：

①窗未满时，以初始化阈值为判断依据。

式中：pi为轨迹的采样点，当pi=正常点时，pi进入滑窗；否则，将pi从轨迹中删除。

②窗满时，根据3σ 原则，对窗内轨迹点的平均速度计算阈值。

式中：E为阈值，meanwin为窗内平均速度，varwin为窗内速度标准差。

当vi>E，pi=离群点，进行剔除；否则，窗体滑动，将窗体中最旧的点移除窗体，令当前点进入窗体，直至整条轨迹结束。

1.1.2 滤噪平滑

采用卡尔曼滤波对轨迹数据进行平滑处理，达到消除轨迹数据中部分误差、平滑轨迹的效果。

1.2 基于轨迹点聚类的航路节点提取

1.2.1 孤立点剔除

Van Winden 等［15］通过统计分析得出结论：同一道路上的轨迹点到道路中心线的距离近似遵循高斯分布。轨迹预处理仅降低了轨迹数据的噪声影响，但噪声仍存在。由于部分轨迹数据中会存在孤立点，偏离航空主干道路的情况，为进一步降低对航路节点提取的影响，本文采用DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法［16］对轨迹数据点进行深度去噪处理。该算法不仅能够对轨迹数据点进行聚类，且对噪声不敏感，能处理非凸数据，较好地识别孤立点。

定义 孤立点。距离航路中心线较远且稀疏的点，如图1 所示。

图1 孤立点示意图Fig.1 Schematic diagram of isolated point

设轨迹{pi，1，pi，2，…，pi，n}，其中pi，j为第i条轨迹的第j个轨迹点，轨迹集合I={T1，T2，…，Tm}，轨迹点集合S={p1，1，p1，2，…，pm，n}。

1）对轨迹点集合S进行DBSCAN 聚类并设置合适的eps和Minpts，可得到聚类结果S1，S2，…，Sk，S-1，其中，S-1为孤立点集合，其余聚类结果视为有效点。

2）将孤立点集合S-1中的轨迹点从轨迹集合I中的轨迹T中剔除。

1.2.2 轨迹重采样

在历史轨迹数据库中，轨迹数据的采样时间间隔不统一，且同一轨迹的采样点的距离间隔也不同，所以本文采用轨迹重采样的方法，能消除采样时间间隔不统一造成的轨迹点的空间密度不同带来的影响，保证各条轨迹数据的轨迹点密度基本一致。该步骤的实现是为了1.2.3 节中的轨迹点聚类做好数据基础。具体算法如下：

1.2.3 轨迹点聚类

对数据库中的历史数据进行处理后得到的每条轨迹大致为等距离采样点，换言之，所有的轨迹数据点的密度较均匀，本文采用mini batchK-means 聚类对所有的轨迹采样点进行聚类，根据数据规模和覆盖面积，设定合适的聚类中心个数，经过聚类后，聚类中心能够较好地反映出轨迹的航路结构，得到航路节点G={C1，C2，…，Cn}。

1.3 对航路节点修正

对航路节点进行提取后，由于上述聚类方法选取聚类中心个数的原因，会存在航路节点分裂现象，即两个或多个节点之间的距离较近，本文采用基于密度的聚类方法，对航路节点进行合并，得到新的航路节点集合G′={C′1，C′2，…，C′n′}，并对轨迹数据点pi所属的节点簇类进行相应的修改，如图2所示。

图2 航路节点修正示意图Fig.2 Schematic diagram of route node amendment

1.4 航路节点连接

根据1.3 节可得到航路节点，将航路节点视为聚类中心，那么每条轨迹Ti={pi，1，pi，2，…，pi，n}的轨迹点pi，j(1≤j≤n)都含有各自的所属类别，本文将轨迹Ti映射到航路节点集合中，每条轨迹就可由Ti={pi，1，pi，2，…，pi，n}转换为由航路节点集合中的元素构成的序列为Ti={C′k1，C′k2，…，C′kn}，其中：{pi，1，pi，2，…，pi，m}∈C′k1，{pi，m+1，pi，m+2，…，pi，m+l}∈C′ki，{pi，m+l+1，pi，m+l+2，…，pi，n}∈C′kn。

轨迹点pi映射到航路节点集合的原则：

式中：distance(p，C)为轨迹点p和航路节点C的欧氏距离。

将所有历史轨迹映射为航路节点集合中的元素序列后，遍历数据库中的所有轨迹，可以得到整个航路节点的连接关系，进而得到航路几何数据。

2 实验与结果分析

2.1 实验数据集

本文根据真实轨迹的运动特征和数据特点，生成仿真数据用于实验。在生成仿真数据时，进行添加噪声、离群点、轨迹断裂等处理，使仿真数据尽可能逼近真实数据。实验数据包括不同噪声强度的轨迹数据，每种噪声强度下包括4 800条轨迹。实验数据集共有2 296 660 个轨迹数据点，每个轨迹点包括经度、纬度、时间等属性。实验数据集如图3 所示。

图3 实验数据集Fig.3 Experimental data set

2.2 实验结果分析

对实验数据集进行预处理（如图4 所示）后，通过对孤立点剔除（如图5 所示），轨迹重采样、轨迹点聚类和对航路节点的修正与连接，得到航路集合数据。针对实验数据集，本文设定聚类中心个数为300，为了对航路节点的提取效果进行评价，本文以仿真生成实验轨迹数据使用的航路结构作为参考，将本文的实验结果与参考航路进行叠加对比分析。

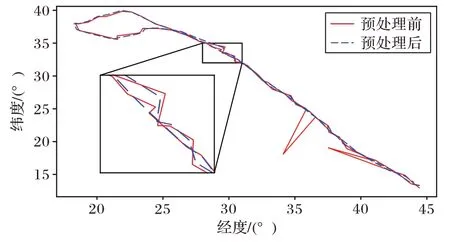
图4 轨迹预处理前后对比Fig.4 Comparison of trajectories before and after preprocessing

图5 孤立点剔除效果Fig.5 Visualization of isolated point removal

2.2.1 定性评价

图6（a）为本文方法的叠加分析图。从整体结果来看，本文方法提取的航路节点基本覆盖了参考航路，并且准确度较高；但对局部结果观察发现，连接航路节点的过程中，部分航路会出现错误连接的情况，这主要是由于轨迹数据中存在的噪声的影响，使得轨迹数据点向航路节点集合中映射出现偏差，导致错误连接。

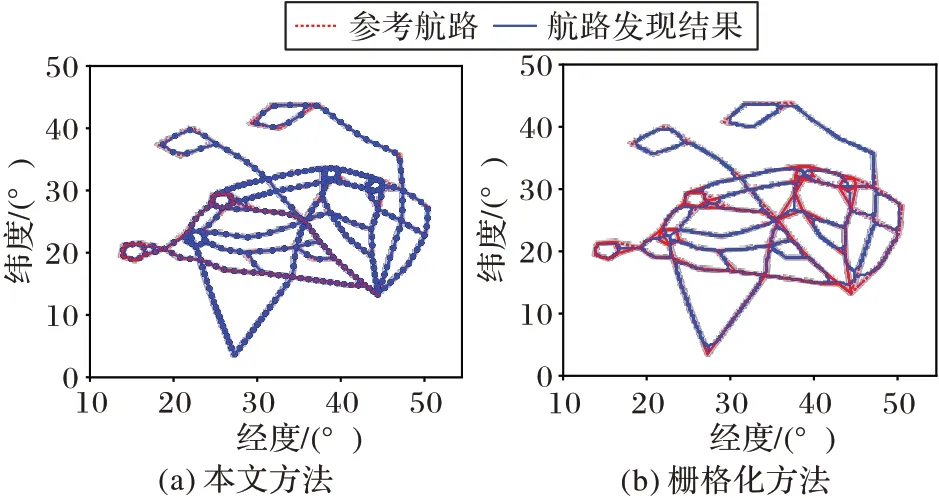
图6 两种方法航路发现结果对比Fig.6 Comparison of results of two route discovery methods

2.2.2 定量评价

为了定量评价本文方法的实验结果，将本文实验结果与栅格化方法［8］的实验结果分别与参考航路进行匹配，然后引用文献［12］提出的缓冲区检测方法，分别建立10 km、20 km、30 km 的缓冲区，对两种方法提取的航路节点的覆盖率α和航路长度的覆盖率β进行性能评价。具体评价函数如下所示：

式中：pi为航路节点，N为航路节点总数，linei为提取的航路中第i段轨迹段在参考航路缓冲区的部分，LINEi为提取的航路中第i段轨迹段。

如图7 和图8 所示，本文方法提取的航路数据在节点覆盖率和长度覆盖率上有较大提高，特别是在10 km 的缓冲区内的实验结果。对单一路段的提取，两种方法的提取效果比较相近，但对于两条航路夹角较小的交汇路口处，栅格化方法易提取成为一条航路；对“圆”状航路结果容易误提取为点结构。相较于栅格化方法，本文方法能够在保持提取平滑航路准确率的基础上，更好地提取“圆”状航路结构和夹角较小的两条航路的航路结构，有较好的抗噪性。

图7 本文方法与栅格化方法的节点覆盖率对比Fig.7 Comparison of node coverage between two methods

图8 本文方法与栅格化方法的长度覆盖率对比Fig.8 Comparison of length coverage between two methods

2.3 方法验证

本文方法的有效性已在真实数据集上得到验证，由于真实数据不便公开引用，所以本文对22 类民航轨迹数据进行航路提取来验证本文方法的有效性。轨迹数据可视化如图9（a）所示，航路提取结果如图9（b）所示。根据民航数据的航路发现结果可知，本文方法能够较好地发现航路，但存在一定的局限性，当某条航路或航路段上的轨迹数目稀少时，该航路或航路段上的轨迹易被检测为孤立点进行剔除，因此漏掉部分航路。

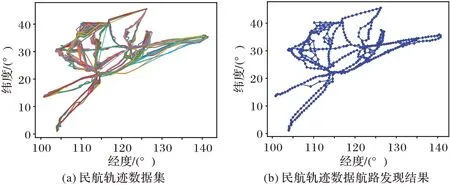
图9 民航轨迹数据实验结果Fig.9 result of civil aviation data set

3 结语

为了快速准确地从航空轨迹数据中提取航路的几何数据，本文提出了一种基于轨迹点聚类的航路提取方法，利用航空轨迹模拟数据进行实验分析，以模拟数据的理想航路为参考数据，与栅格化方法进行定性定量分析评价，结果表明本文方法提取的航路数据在节点覆盖率和航路长度覆盖率上都有明显提高，而且本文方法易于实现，有一定的有效性和可靠性。

本文方法提取的航路节点，可将轨迹数据映射为节点序列，进而可将轨迹预测问题转化为序列到序列的序列预测问题。为提高预测问题的正确率，需进一步研究和完善：1）轨迹数据映射到节点集合中的更有效的方法；2）各个航空路段的轨迹数据的密度相差较悬殊的情况，本文方法还需要进一步改进；3）由于噪声的影响，连接航路节点时会有误连的情况，下一步需对连接节点的方法进行进一步研究。