基于E-CARGO模型的共乘出行匹配建模与优化方法
2022-04-12李晓会董红斌
李晓会,董红斌
(1.哈尔滨工程大学计算机科学与技术学院,哈尔滨 150001;2.哈尔滨职业技术学院电子与信息工程学院,哈尔滨 150081)
0 引言
近几年,随着私家车数量的迅速增长,城市的交通压力越发紧张。城市汽车保有量的增多,在方便出行之外,也带来了一系列问题,如交通拥堵、石油资源过度消费、环境污染等。共乘出行已被证明是充分利用交通资源、缓解停车位紧张、减少环境污染和优化社会效益的有效途径[1]。车联网和全球实时定位等技术为共乘出行应用系统提供支持和保障。如何利用计算机技术,提高共乘出行系统中司机和乘客的匹配效率,已受到更多学者的关注和研究。此外,共乘出行系统可以使乘客和车主(司机)分摊共乘出行的相关费用,例如燃油费、过路费等,这部分费用相当可观。随着移动互联技术的不断进步和互联网移动设备的普及,简单、安全、灵活、高效和经济的共乘出行系统未来将会更受欢迎。
共乘是指具有出行路径相同或相似的乘客按照某一匹配方式乘坐被分配的同一辆汽车,在某一行驶区间共同乘车并分摊出行费用的一种出行方式。共乘出行应用系统主要考虑结合地理位置和时间信息来完成最优定价策略和车辆调度策略[2]。在共乘出行应用系统中,可以按乘坐请求在途中与有空座位的车辆匹配。乘客发出要出行的出发地点、时间和目的地,应用系统根据某一定价规则返回用户大约需要支付的费用,乘客接受费用后可以匹配给一位邻近的司机:如果是单司机多乘客模式,当司机驾驶的汽车还有空座位,可以接受多名路径相似的乘客分配一起乘车,完成出行后平台系统进行结算;如果是单司机单乘客模式,那么每次司机只能匹配一名乘客发送的请求,将乘客送达目的地后才会进行下次匹配。
司机可能只接受一个乘客的搭乘,在座位空余的情况下也可能愿意接受多个乘客。同样,每个乘客可能选择独自搭乘司机的车,也可能愿意和其他乘客共乘,存在的司机和乘客之间的共乘关系如表1 所示。无论哪种出行选择,乘客与司机的匹配方法都是共乘出行系统的核心。

表1 出行乘客与司机之间的关系Tab.1 Relationship between passengers and drivers
本文主要对乘客和司机进行在线动态匹配进行研究,结合基于角色的协同(Role-Based Collaboration,RBC)及其E-CARGO(Environment-Class,Agent,Role,Group and Object)模型[3-6],对共乘匹配问题进行建模,并对共乘中的代理、角色和群组及它们之间的关系进行了抽象描述,将共乘优化问题形式化为一个组角色分配问题,给出形式化定义和目标函数。通过在一定可接受的灵活时间内,在空余座位数约束下,最大化平台系统收入来获得最优匹配、增加平台收入和最大化社会效益。在群组角色指派基础上,在司机乘客利润收入距离矩阵上采用Kuhn-Munkres(K-M)算法[7-9]和Java 中的ILOG 软件包求解获得最优匹配矩阵和时间。
1 相关工作
共乘出行可以让车主节省相关的费用,提高无车用户交通出行的便捷性。共乘服务可能由私家车提供也可能由公共服务商提供。如果系统是私有的,以盈利为目的,那么提供商可以得到佣金或广告收入;如果是公共系统,可能会有一个社会目标,比如减少污染和交通拥堵。但无论共乘出行系统的性质是什么,都需要完成司机和乘客的匹配,一般来说在匹配中需要考虑的具体目标有:最小化系统中车辆行驶里程,尽量减少系统中的行驶时间和最大化参与者人数。共乘出行中匹配的成功率是吸引大家参与共乘出行系统中的一个重要性能指标,高成功率会刺激更多的参与者参与进来,本文针对共乘匹配建模与优化方法进行了研究。
共乘出行应用一般都需要乘客提供出发时间,因此有很多研究通过时间窗来获取参与者的时间偏好。文献[10]中研究限制用户在一定路程中应花费的时间,在应用研究中,允许乘客指定他们愿意接受的比直达时间多出的最大超额时间。乘客通过共乘出行系统发送请求的时间,最早出发时间和可以接受的抵达目的地时间关系如图1 所示。

图1 共乘中乘客时刻信息Fig.1 Time information of passenger in ride-sharing
文献[11]中提出了一种新固定时间下的形式化攻击建模和影响分析方法,验证了篡改控制设置对交通和驾驶员的成本影响。通过研究表明,人们更在意的是出行时间得到保证。影响乘客和司机匹配的因素除了时间因素外,也会有其他因素影响匹配是否成功,例如,人们可能更喜欢和比较熟悉的人共乘一辆车,女性乘车时感觉女司机更有安全感等。总之,对潜在的乘客在选择共乘伙伴时的限制越多,就会越难为该乘客找到成功的匹配[12]。
人们选择共乘出行除了考虑时间因素,也希望通过选择共乘出行方式分摊出行成本,降低花销。因此,也有很多学者研究关于在共乘中费用的分摊方式。文献[13]中研究了各种成本分担策略,提供了成本分摊策略维持参与或减少车辆使用的必要条件;文献[14]中考虑到乘车距离的不同,提出按距离远近成比例分摊费用的方法;文献[15]中提出了一种基于拍卖机制来确定司机报酬的方式,这种方式考虑到对司机的评估,对司机来说,他们心中愿意支付的费用介于单独驾驶私家车的费用和乘坐出租车的费用之间,对司机的补偿和佣金越高,司机心理对弯路的可接受长度越长;文献[16]中针对共乘市场准入限制较少、对服务定价的监管也较不严格的现状,从经济学的供需角度研究劳动力供给的参与弹性和工时弹性对市场劳动供给的影响;文献[17]中研究激增定价策略,按其动态价格向提供商支付固定佣金,并得出使用激增定价策略下,所有利益相关者都可以从具有自调度能力的平台上中获益这一结论。
在共乘出行时,如果司机时间足够灵活充裕,他们可能愿意为多个乘客提供服务,或是一个接一个,或是同时搭乘多名乘客。在为一个司机指派多名乘客时,系统会提供可行的最优路线,尽量减少出行成本。文献[18]中提出并构建了实时大容量乘车共享的数学模型,该模型可扩展到大量乘客和出行,根据在线需求和车辆位置动态生成最优路线。文献[19]中提出一种基于构造和局部搜索的启发式方法来研究多个乘客共乘的时间模型。
E-CARGO 模型在指派问题和推荐系统[20-23]中得到了一定的应用。文献[20]中针对根据基站代维人员结构情况优化人员分工与指派这一问题,通过E-CARGO 模型对基站代维任务进行建模和实验仿真,实验表明该方法高效、可靠;文献[21]中使用E-CARGO 模型对资源分配进行建模,并提出多对多推荐问题的优化求解方法。共乘出行问题属于资源分配问题,本文基于角色协同的工程理论方法和E-CARGO模型对共乘出行系统进行抽象和建模。
2 数学模型
2.1 E-CARGO模型介绍
E-CARGO 模型是由加拿大学者朱海滨教授基于角色协同理论的研究与探讨提出的一种基于角色协同的模型[24-26],是角色分配基本理论的研究和扩展,适用于社会系统和经济系统的形式化分析建模。在E-CARGO 模型中,系统Σ可以描述为一个九元组,即。其中:C是类集,O是目标集,A是Agent 集合,M是消息集合,R是角色集合,E是环境集合,G是群组集合,S0是系统的初始状态,H是用户集合。系统中,A和H、E和G是紧耦合集,一个用户和他的Agent 可以一起扮演一个角色,每个群组都在一个环境下工作运行,环境对群组有规范作用。在ECARGO 模型中,所有的Agent 都仅有一个中心处理事务,每个Agent 在一个时间内只扮演一个角色。
现实中的很多系统均可抽象表示映射到E-CARGO 模型中,将问题本身或将问题分解成子问题:首先确定角色和Agent,然后通过约束来描述角色或Agent 之间的关系和限制约束,再按角色和群组进行指派,最后通过评估准则对指派结果进行循环指派和评估,确定最终指派方案。
2.2 E-CARGO模型对共乘问题建模
在共乘出行系统中进行乘客和司机匹配时,要考虑可接受的时间范围、利润收入和空座情况进行车辆调度匹配和换乘方式。乘客为了节约出行费用和时间,有时从出发点到目的地过程中可能需要换乘匹配多个司机。
定义1共乘出行系统平台中司机角色R(Role)。R∷=。其 中:n表示司机角色的ID编号;表示共乘系统司机角色处理的消息集合;Ac表示当前扮演该角色的Agent 集合,即与该司机匹配的乘客集合;Ap表示可以扮演该角色的Agent 集合,即可以匹配的乘客集合;No表示扮演该角色的Agent 可以获取到的对象集合,主要包括共同顺路搭乘的乘客;Q1 表示Agent 扮演该角色所需的最小评估值,即出行费用。在共乘出行系统平台下,角色R表示等待接受调遣指派的汽车司机。
定义2共乘出行系统乘客代理A(Agent)。A∷=。其中:n表示此乘客代理的ID 编号;Rc表示此代理正在扮演的角色,即正在乘坐的汽车司机;Rp表示此代理将来可以扮演的角色集合,即将来换乘匹配的汽车司机;Ng表示此代理所属的群组号;Qr表示此代理对角色集合中每个角色的评估值。在共乘出行系统平台下,Agent 表示发出出发时间、地点和目的地请求的乘客。
在三维遥感影像可视化建模之前,必须先对各幅DEM文件进行镶嵌,利用三维遥感解译软件ArcScene来实现三维地形的可视化建模,将DEM和DOM切片的地形数据和遥感数据为信息源,形成三维遥感影像(图4)。
定义3为司机匹配的乘客向量L是在一定时间范围内,每一个司机可匹配乘客数的向量。
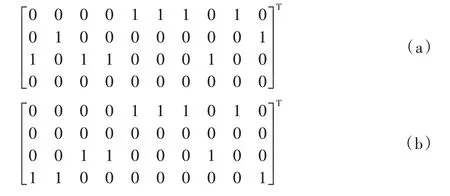
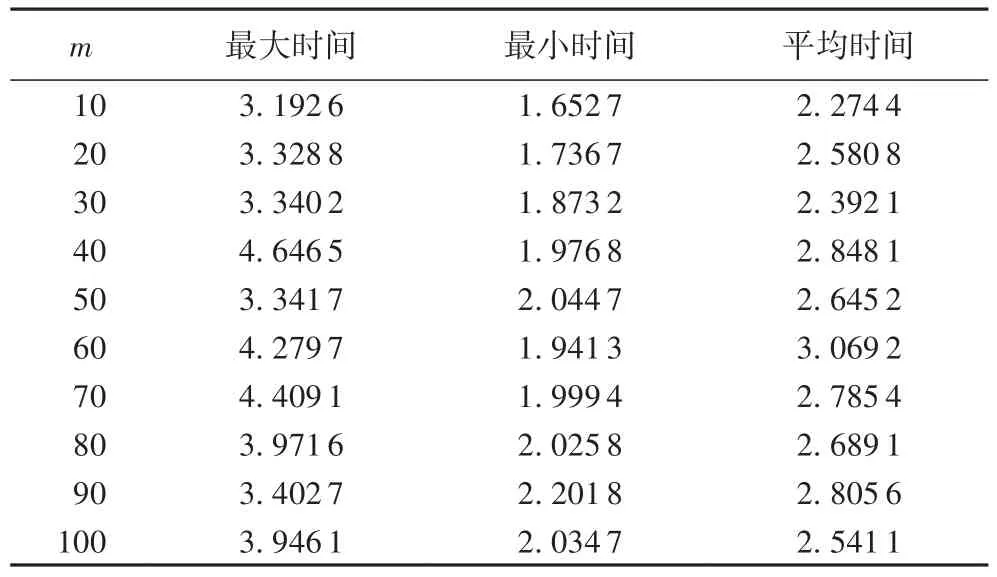
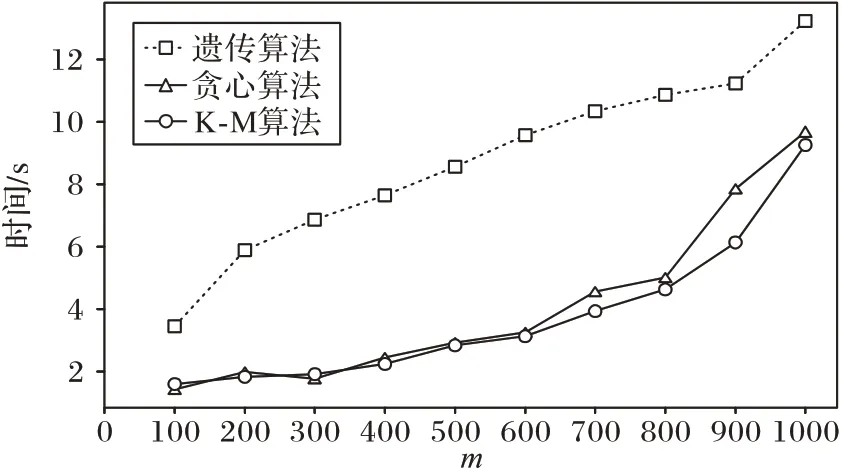
定义4司机接送乘客的利润收入矩阵Q是一个m×n矩阵,其中Q[i,j]代表司机rolej(0≤j 定义5匹配矩阵T是一个m×n的矩阵,其中T[i,j]代表Agenti是否匹配搭乘司机rolej的车:T[i,j]=1 代表搭乘;T[i,j]=0 代表不搭乘;T[2,2]=1 表示指派第3 个代理(乘客)到角色(司机)3 的车辆上乘坐。 定义6当司机角色R同一时间段搭载乘客数量≤最大载客量时,称司机角色是可运行的,即。 定义7乘客从出发地到目的地可能多次换乘,La[i](0≤i 定义8司机角色范围向量记为L[j]∈N(0≤j 定义9总行收入r为匹配矩阵T之后,所有司机收入之和,即:。总收入的求解过程:将利润收入矩阵与分配矩阵进行矩阵点乘。 目标函数为: 约束为: 案例分析 假设在一定可接受的接送乘客距离范围内,有10 名乘客同时呼叫乘车,有4 名司机可调用派遣,车型均为5 座小汽车,乘客不换乘,根据司机距离每名乘客远近及接送距离产生的利润收入矩阵如下: 分配矩阵可能如下: 当按(a)分配矩阵进行调度总收入为73,按(b)分配矩阵进行司机派遣送收入为81,且L(a)=[4,2,4,0],L(b)=[4,0,3,3],即在分配方案(a)中第4 位司机没有匹配到乘客,在分配方案(b)中第2 位司机没有匹配到乘客。 K-M 算法[7-8]的时间复杂度为O(m3),优于穷举搜索法。可以将上述问题转化为整数规划来进行求解最大匹配矩阵T,算法的伪代码描述如下: 算法1 Kuhn-Munkres 求解最优匹配算法。 输入 司机角色数量n,乘客代理数量m,n维角色搭载乘客数量向量L,同时乘客换乘向量La,m×n司机接送乘客的利润收入矩阵Q; 输出 最优匹配矩阵T和时间。 实验在Microsoft Windows 10 Home 操作系统下实现,其中CPU 配置为AMD Ryzen 5 PRO 3500U w/ Radeon Vega Mobile Gfx 2.10 GHz,内存为8 GB,软件环境为Version:Eclipse Java Oxygen(4.7.3),JDK 的版本是1.8.0_181。乘客和司机的距离矩阵Q中的值随机生成,取值范围1~10;司机数值分别取10~100 进行实验,最优匹配时间如表2 所示。 表2 不同Agent数量下匹配算法时间 单位:msTab.2 Matching algorithm time with different number of Agents unit:ms 本文将采用的K-M 算法与ILOG 软件包算法进行了比对,通过实验发现:使用ILOG 软件包求解时,相似规模的问题都会消耗相似的时间,且时间长。使用K-M 算法时,在Agent 数量m(m<400)一定规模下,所需时间增长缓慢;当Agent 规模大于某一数量(400 将K-M 算法与遗传算法[27]、贪心算法[28]进行对比,设Agent 数量为0~1 000,小汽车L[j]最大同时搭载乘客数为4,群体大小为50,终止进化代数为150,交叉概率为0.5时,所花平均时间如图3 所示。可以发现当仅考虑到局部最优时贪婪算法时间开销与K-M算法相差不多,但在约束限制下,满足全局最优目标函数时,贪婪算法时间开销较大。对比遗传算法,在Agent 数量相同时,贪婪算法和K-M 算法在共乘匹配中时间平均减少了60%。 图2 不同Agent规模下ILOG软件包算法和K-M算法时间性能Fig.2 Time performance of ILOG software package algorithm and K-M algorithm with different number of Agents 图3 不同Agent规模下三种算法时间性能比较Fig.3 Time performance comparison of three algorithms with different number of Agents 本文主要研究在共乘出行系统中,空余座位数有限和允许乘客多次换乘的约束条件下,基于E-CARGO 模型对共乘出行问题进行形式化建模,并应用K-M 算法求解最优匹配矩阵。通过实验应用K-M 算法和ILOG 软件包求解最优匹配矩阵,并进行时间性能对比分析。在未来的工作中,将深入研究匹配组合优化求解方法,提高匹配率和时间性能以满足动态共乘匹配的实时需求。如何基于E-CARGO 模型进行定价和匹配来吸引越来越多乘客和司机参与共乘出行系统也是未来我们要研究的方向和内容。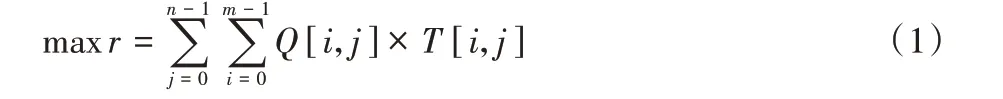


2.3 算法分析

3 实验分析

4 结语
