混合伊藤算法求解多尺度着色旅行商问题

2022-04-12韩舒宁徐敏董学士林青沈凡凡

计算机应用 2022年3期

韩舒宁，徐敏，董学士*，林青，沈凡凡

（1.青岛大学计算机科学技术学院，青岛 266071；2.长江航道规划设计研究院，武汉 430040；3.南京审计大学信息工程学院，南京 211815）

0 引言

目前关于着色旅行商问题（Colored Traveling Salesman Problem，CTSP）的研究主要包括：利用遗传算法（Genetic Algorithm，GA）、贪心法遗传算法（Genetic Algorithm with Greedy initialization，GAG）、爬山法遗传算法（Hill Climbing Genetic Algorithm，HCGA）和模拟退火遗传算法（Simulated Annealing Genetic Algorithm，SAGA）等来求解CTSP［1-2］，而且还对CTSP 进行了扩展，提出了连续着色旅行商问题（Serial Colored Traveling Salesman Problem，SCTSP）［3］；将离散伊藤算法（Discrete ITÖ algorithm，DITÖ）用于求解小尺度CTSP（即CTSP 城市数小于等于101）［4］；探讨了伊藤算法（ITÖ algorithm）的收敛性与收敛速度，并将其应用于求解旅行商问题（Traveling Salesman Problem，TSP）［5］；利用基于伊藤过程的混合算法求解着色瓶颈旅行商问题［6］，并将混合遗传算法和伊藤算法应用于求解多平衡旅行商问题［7］；结合均匀设计（Uniform Design，UD）与混沌理论［8］来对蚁群（Ant Colony Optimization，ACO）算法的参数进行优化；探讨了基于UD 的GA 与ACO 算法求解TSP 参数优化［9］；设计了一种基于多任务学习的ACO 求解CTSP［10］；将CTSP 扩展到大规模，并应用一种改进的蜂群算法求解大尺度CTSP［11］；给出了一种基于伊藤过程的遗传算法以解决大尺度的着色平衡TSP［12］；提出了一种变量邻近搜索的混合遗传算法求解多尺度多瓶颈TSP［13］；应用一种基于种群的增量学习算法求解一类连续CTSP，并设计了一种变量邻近搜索算法解决CTSP 变种问题［14］；应用三角网可变邻域搜索方法求解大规模一般CTSP（general CTSP）［16］等。

伊藤算法是由董文永等［5］首次提出的一种群体智能算法，可用伊藤随机积分的方法建立该算法的动力学方程，而漂移和波动操作是全局优化的关键点。由于伊藤算法在求解组合优化问题具备一定的优势，因此本文结合CTSP 的特点，设计了一种基于UD 融合ITÖ 和ACO 的混合伊藤算法（Hybrid ITÖ Algorithm with Uniform Design，UDHITÖ）来求解该问题，并将研究问题的尺度扩展到大尺度，即CTSP 的城市数目大于101。本文主要工作如下：用粒子来表示CTSP 的解，一定量的粒子可以构成粒子系统，并应用伊藤随机积分的方法建立算法的动力学方程，每个粒子的运动包括漂移和波动两种。为了使伊藤算法能够求解组合优化问题，UDHITÖ 首先借鉴ACO 的思想构建产生CTSP 的可行解的概率生成模型，然后采用伊藤算法的漂移和波动算子来更新，如此循环，直到找到满意的解为止。实验结果表明，UDHITÖ求解CTSP 的最优解和平均解要优于对比算法。

1 混合伊藤算法求解CTSP

1.1 基于图的概率生成模型

混合伊藤算法UDHITÖ 采用城市数排列为编码方法［4］。对于组合优化问题，使用ACO 的基于图的概率生成模型来构建一个可行解的方法已被证实是可行的，因此，UDHITÖ使用该方法来构建一个CTSP 的访问序列。例如一个CTSP实例，每条i到j的边有两个影响因素：一个是活动强度，由τ（i，j）决定；另一个是距离，由d（i，j）表示。从起始点开始去生成一个可行解，ACO 概率选择公式如下所示：

其中：η（i，j）表示距离d（i，j）的倒数；tabu表示禁忌表，用来存储已被访问的城市；α是在选择概率中控制边权重的参数，β为控制可见度的参数。用ACO 的思想构建CTSP 可行解的步骤［4］如下所示：

算法1 ACO 构建CTSP 可行解。

1.2 UDHITÖ设计

设计UDHITÖ 共有五个部分，包括粒子半径、环境温度、活动强度、漂移算子和波动算子。该算法具体设计如下：

1）粒子半径。式（2）指适应度值与粒子半径的关系，适应度值越好，粒子半径会越大，活动强度会越弱。

其中：x表示当前种群的一个粒子，f（x）代表适应度值，g（x）表示单调函数。N个当前种群的粒子根据适应度值的等级按照从最好到最差的顺序分类，结果用x1，x2，…，xN来表示。粒子半径由下列公式［6-7］计算：

其中：rmax和rmin分别表示最大和最小的半径，所有的半径被均匀分布在rmax和rmin之间。如果是缺省值，rmax设置为1，rmin设为0。

2）环境温度。环境温度可以用下面的方法来计算：

其中：Ti表示第i个规划时间的温度；ρ表示退火系数，它能控制温度降低的速度，缺省值的情况下ρ=0.9。

3）活动强度。根据爱因斯坦的大分子运动和粒子热力学运动定律，粒子活动强度与粒子半径成反比，与温度成正比，因此当前种群的粒子xi的活动强度δi可由式（5）［6-7］来计算：

其中ri表示粒子xi的半径。

4）漂移和波动算子。漂移可以吸引粒子向最优粒子（吸引元）移动，在求解过程中，可增加被最优粒子所访问的路径信息素浓度；波动是一种受环境影响的随机分布，在环境中，它随机选择一些路径来增加信息素浓度。所有路径信息浓度将会蒸发以保持整个信息素浓度的平衡。具体设计步骤如下所示：

a）所有路径的活动强度τ将蒸发，其中，ρ是挥发因子。

b）所有的粒子按照适应度值来分类，最小的设置为最好，因此，第一个粒子是当前最好的粒子，其他的粒子会向它漂移。

c）按照上面的a）与b）顺序，更新每个粒子的解。

漂移算子可通过式（7）更新当前路径和最优解路径上的活动强度τ。其中：σ表示当前解，使活动强度δi等于信息素增量δ；σ′表示当前最好的粒子，或当前最好解。

UDHITÖ 波动算子如式（8）所示，以求解CTSP 为例，城市之间路径的活动强度用τ表示，当前粒子漂移强度为δ，σ″代表未被访问的路径，漂移强度（信息素增量）等于活动强度δi，rand（）为随机函数，可产生一个［0，1）的随机数，p为选择随机路径的概率。

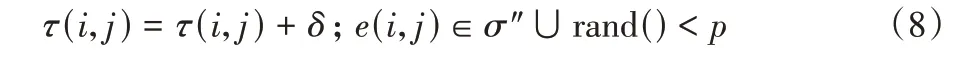
1.3 UDHITÖ的步骤

UDHITÖ 有漂移和波动两个操作，漂移运动表示每个粒子向自己的吸引元运动，漂移强度函数依赖于它的适应度值、半径和环境温度。波动强度函数依赖于粒子半径、适应度值和环境温度。UDHITÖ 的设计流程如下：

算法2 UDHITÖ 算法求解CTSP。

2 实验与结果分析

本文实验所用数据一部分来自于文献［1］，表1 中城市数量n从21～101 的数据即可以直接从该文中下载；另一部分数据，也就是城市数量大于101 的数据，是根据CTSP 的要求，由最原始的TSP 数据制作而成，该原始数据的名称为TSPLIB，可由http：//people.sc.fsu.edu/～jburkardt/datasets/tsp/tsp.html 下载。

表1 实验采用的CTSP实例Tab.1 Examples of CTSP in experiments

实验计算机环境为：Intel Core i7-6700 CPU，3.40 GHz处理器和8 GB RAM。实验对比算法DITÖ 的参数设置［4］：种群M=30，α=5，β=3，随机选择概率p=0.3，初始温度T=1 000，ACO 对应的参数设置与DITÖ 相同。GA、GAG、HCGA和SAGA 的参数设置与文献［1］中相同算法一致，算法参数设置情况为：种群大小=30，交叉概率=0.7，变异概率=0.1。SA 算法的初始温度=100，总的冷却时间=60，冷却系数为0.9。HITÖ 的参数随机设置，UDHITÖ 的参数设置通过UD方法得到。本文算法最大的未更新迭代次数为60，即算法终止条件。本实验对比的GA、GAG、HCGA 和SAGA 均来自文献［1］；DITÖ 来自文献［4］；ACO 来自文献［9-10］；HITÖ 是未采用UD 的混合伊藤算法。

为了有效验证算法，本文实验采用不同尺度的数据，CTSP 的实验数据如表1 所示。

本文混合伊藤算法UDHITÖ 的参数设置通过UD 获得。UDHITÖ 是一种基于ACO 的混合算法，其均匀设计参数选择可参考ACO 实例［8］，算法均匀设计如表2 所示（括号内值表示算法的参数组合数值）。表2 中，UDHITÖ 共有15 种参数组合，采用这些参数设置，UDHITÖ 求解101 个城市的CTSP的最优解和平均求解质量如表3 所示。从表3 可看出，第8种参数组合的UDHITÖ 求解101 个城市CTSP 的最优解和平均解最好，第3 种参数组合的伊藤算法求解101 个城市CTSP求解质量最差，从而得出UDHITÖ 的参数设置是种群M=30，α=4.48，β=4.77，随机选择概率p=0.448。

表2 参数组合的测试集实例Tab.2 Test set examples of parameters combination

表3 基于表2中15种参数组合的UDHITÖ 求解101城市CTSP的最优解与平均解单位：kmTab.2 Optimal and average solutions of UDHITÖ algorithm for 101-city CTSP on 15 parameters combinations from Tab.2 unit：km

表4～6分别为GA、GAG、HCGA、SAGA、ACO、HITÖ、UDHITÖ 等算法求解小、中、大尺度CTSP 的实验结果对比，表中最优解和平均解分别表示算法运行30 次的最优解和平均解。

表4 各算法求解小尺度CTSP的最优解与平均解单位：kmTab.4 Optimal and average solutions of different algorithms for small scale CTSP unit：km

表5 各算法求解中尺度CTSP的最优解与平均解单位：kmTab.5 Optimal and average solutions of different algorithm for medium scale CTSP unit：km

表6 各算法求解大尺度CTSP的最优解与平均解单位：kmTab.6 Optimal and average solutions of different algorithm for large scale CTSP unit：km

从表4～6 可以看出，算法在求解CTSP 的求解精度相差不大，UDHITÖ 的求解质量优于GAG、HCGA、SAGA、ACO、HITÖ 等对比算法；当求解大尺度的CTSP 时，从求解质量来看，UDHITÖ 的效果最好，其次是DITÖ、ACO 和SAGA。

UDHITÖ 求解多尺度CTSP 的求解质量不仅优于对比文献中的SAGA、HCGA、GAG、GA，也优于DITÖ、HITÖ、ACO，表明基于均匀设计的混合伊藤算法UDHITÖ 求解CTSP 是有效的。UDHITÖ 是一种群体智能算法，运用均匀设计进行参数优化，使用波动算子和漂移算子来完成解的更新，UDHITÖ自身的特点使其有较强的自适应能力和全局搜索能力。