一类Choquard型方程解的存在性

刘丽娟

(太原师范学院 数学系， 山西 晋中 030619)

0 引言和主要结果

近年来，一类Choquard方程，如

(1)

被广泛关注.

当V(x)为不同位势，方程带有不同的扰动项时，该方程解的情况将有所不同.当V(x)=1+μh(x)，g(x,u)=0，文献[1]运用临界点理论证明方程至少存在一个基态解；当V(x)=1+μh(x)，g(x,u)=f(x)，文献[2]运用Eklend变分原理和山路引理证明方程存在两个正解；当V(x)→0，|x|→+∞且g(x,u)=0，文献[3]证明方程存在一个正解；文献[4]证明方程(1)满足V(x)→+∞，x→+∞且g(x,u)=f(x)时两个非平凡解的存在性.关于Choquard方程带有不同扰动项及V(x)为不同位势的更多研究可参看文献[5-12].

受上述结论的启发，我们研究问题

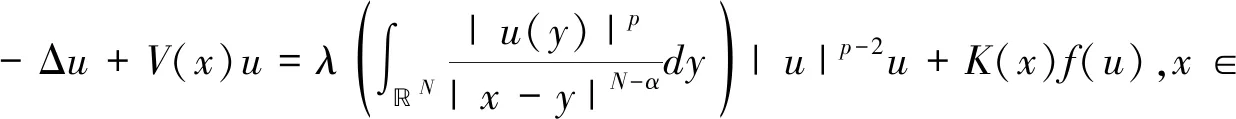
(2)

(Ⅱ)如果{An}⊂N是一个Borel集合列，且存在R>0,对所有的n都有‖An‖≤R,那么一致成立；

(K1)

(K2)

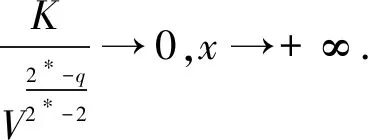
(K3)

f满足条件：

(f3) 存在2p>θ>2，使得0<θF(t)≤tf(t)，∀t∈,其中F(t)=f(t)dt.

我们得到以下主要结果：

定理1 假设(V，K)∈K并且(f1)～(f3)成立，则方程(2)至少存在一个解.

1 预备知识

记D1,2(N)是C∞(N)在范数下的完备化空间，令

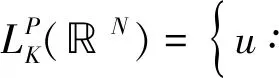
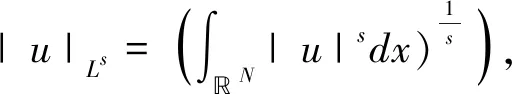
其上的內积为

由它所诱导的范数是

定义Iλ(u)为方程(2)对应的能量泛函，即

其中

根据文献[2]，由Hardy-Littlewood-Sobolev不等式可知,当

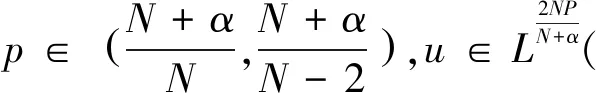
由此可得Iλ(u)∈C1(E,).如果u满足

则称u∈E为方程(2)的解.易知如果u是Iλ(u)的非平凡临界点，则u是方程(2)的解.

为了证明定理1，我们先证明如下引理：

引理1 如果(V，K)∈K并且(f1)～(f3)成立，则Iλ(u)在E中满足(PS)条件.

证明假设{un}⊂E是Iλ的一个(PS)序列，则存在c>0.当n→∞时，有

接下来证明{un}有界.由于

(3)

由文献[7]和[13]可知

H(un,un)→H(u0,u0)

(4)

(5)

结合式(3)、式(4)、式(5)可得

(6)

又因为

(7)

由文献[7]和文献[14]可知

H(un,u0)→H(u0,u0)

(8)

(9)

结合式(7)、(8)、(9)可得

(10)

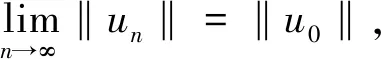
2 定理1的主要证明

对于任意的u∈E，由范数的定义和Sobolev嵌入可知

令Sρ∶={u∈E∶‖u‖=ρ}，如果(K2)成立，根据(f1)～(f2)[14]，对于任意的ε>0，存在Cε>0,使得

|f(t)|≤ε|t|+Cε|t|2*-1,∀t∈.

则

另一方面，如果(K2)成立，根据(f1)～(f2)，对于任意的ε>0，存在Cε>0,使得

|f(t)|≤ε|t|2*-1+Cε|t|,∀t∈.

则

由此可知,当ε→0，τ→+∞，λ>0时，Iλ(τu)<0.因此存在τ1>0，满足u1=τ1u∈E时，‖u1‖>ρ,Iλ(u1)<0.根据山路引理[15]可知存在{un}⊂E，满足

如果(K3)成立，结论同理可证.

由引理1可知,{un}有一个收敛的子列，因此存在uλ∈E，使得在E中，un→uλ，由此可得方程(2)至少存在一个解uλ.

3 总结

本文主要考虑了一类带消失项的Choquard型方程，通过证得能量泛函Iλ(u)满足(PS)条件且当λ>0时，Iλ(u)具有山路引理的几何结构，从而证明了方程(2)至少存在一个解.后续可以继续研究该方程第二个解的存在性.