基于Lingo软件的货物配送方案研究

刘明燕

（山东中医药大学，山东 济南 250355）

随着人们生活水平的提高，运输业在经济生活中的地位显得越来越重要。据统计，运输成本占物流总成本的35%～50%，占商品价格的4%～10%[1]。因此，如何降低运输成本对降低物流总成本具有十分重要的意义。从20世纪开始，前人就对物流配送做了大量研究，经过长期发展，美国、日本等发达国家已经建立起了一套适合本国国情的现代物流配送业，对物流配送方案的研究也较为成熟。FAKHRZAD等[2]建立了一个模糊多目标规划模型（FMOPM），研究并使用LP度量方法，使运输和劳动力的总成本、运输过程中的二氧化碳排放量以及产品从农场到工厂、从工厂到零售商的配送时间最小化，并使总食品腐烂最小化。LU等[3]针对带时间窗的时变车辆路径问题（TDVRPTW），考虑车辆总质量和行驶速度对能耗因子的影响，提出了一个油耗最小化优化函数，采用蚁群算法求解TDVRPTW，优化配送方案。LIU等[4]利用Dijkstra算法对其进行改进，建立了以客户物流成本最小为目标的路径选择模型，使客户物流总成本最小，路径选择模型能够准确地描述物流配送问题。

与国外相比，国内的物流配送方案研究就慢了很多。罗平娟等[5]基于K-means算法的基本思想，使用Python语言结合当地物流配送的实际需求设计了一个合理、实用、有效的配送方案。于江霞等[6]根据客户的消费行为将客户分为多个层级，并构建出基于客户分类的即时配送路径优化模型，根据问题特点设计遗传算法求解。孙丽君等[7]以配送成本最小化为目标，针对多种横向转运配送方式下的成品油配送方案优化问题，构建了可同时表达多种配送方式的优化模型，设计了能够同时求解多种配送方式下的启发式算法以及配送方案。柳清源[8]综合各种证券的因素，确定投资组合方案，明确问题的决策变量、目标函数和约束条件，从而得出问题的基本模型。然后根据实际条件，在基本模型上做更改，运用Lingo进行投资组合线性规划策略分析。钱业洪[9]利用Lingo研究线性规划问题中各参数、变量之间的内在联系。

由此可见，国内外专家学者已经对运输方案进行了较为深入的研究，得出了较为合理的结论，在此基础上，文章对前人经验进行总结，提出以最小化运费为目标建立数学模型，采用表上作业法和Lingo对实例分别进行计算的形式，来验证所建数学模型的有效性。

Lingo是由美国Lindo系统公司开发的专门用于求解最优化问题的软件包，其执行速度较快、输入方便、可用于求解及分析数学规划问题等，所以在数学、科研和工业界均得到较为广泛的应用。Lingo是用来求解线性与非线性优化问题的便捷工具，其内置了求解最优化模型的语言，可以方便快捷地对数学模型进行求解并分析结果。

1 配送问题常见的研究方法

需求点的货物配送问题是一种最常见的物流运输问题，配送运输一般是指距离较短、批量较小以及配送次数较多的一种运输方式，它可由生产厂家直接给货物需求点供货，也可由中间配送站或者其他途径配送到货物需求点。目前常用的解决配送问题的常见方法主要有线性规划法、表上作业法、最短路径法、最小费用最大流法、节约里程法等。

表上作业法是指采用列表的方式来求解线性规划问题中运输模型的计算方法，是线性规划问题的常用求解方法，其实质就是采用单纯形法对线性规划问题进行求解，其基本步骤可分为：①采用西北角法、最小元素法或者最大差额法计算出初始基本可行解；②求出各非基变量的检验数，判断是否达到最优解，如果达到最优解则停止计算，否则进行下一步，用位势法计算；③改进当前的基本可行解，采用闭合回路法调整；④重复步骤②和③，直到找到最优解为止。

2 配送问题的数学模型

2.1 问题的提出

配送方案的设计是运输规划中的一个重要环节，它关系到整个运输过程的时间长短和费用的高低，配送方案的设计应满足以下原则：力求满足所有需求点的货物需求、运距最短、费用最省。现实生活中，常常会遇到多个货物仓库、多家货物需求点的货物配送问题，根据实际工作经验对货物进行调配往往会出现场面混乱、配送时间延长、运输成本提高等问题，因此，在进行配送之前做好配送方案规划就显得尤为重要。本文讨论的是在以总运费最小为目标对货物配送方案进行设计。

2.2 模型的假设

为更好地满足每个货物需求点的需求，在货物配送点与需求点之间构建一系列配送区域，需要拟定一系列假设条件，使货物配送点与各个需求点所形成的配送系统的物流总成本最低。为了方便建立数学模型，作出如下假设：已知配送点到需求点之间运输的单位价格；配送点把货物运往各个货物需求点是同时并列进行的；配送点只输出货物，需求点只接收货物；除了运价以外，不考虑其他一些影响费用的因素。

2.3 模型的建立

假设从配送点Ai到需求点Bj运费的单价为Cij，从配送点Ai到需求点Bj的运输量记为Xij，由此可得总运费为；按常理，第i个配送点的运出量应小于或等于该地的生产量，即第j个销地的运入量应等于该地的需求量，即

由此可得运输问题的数学表达式为：

3 配送方案选择案例

某医药公司有3个仓库A1、A2、A3，该公司4月份药品在这3个仓库中的库存分别为100 t、95t、110t，另外知道有4家大型医院（S1、S2、S3、S4）需要该公司的药品，他们的需求量分别是50 t、80 t、55 t、75 t。如何利用现有库存资源满足这4家医院的药品需求，并使总运输成本最低。从3个仓库向4家医院送货的运输成本价（元/t）如表1所示。

表1 单位运价表（单位：元/t）

本文谈论的是以运费最小化为目标选择货物配送方案，在运费最小化的前提下，还需要考虑以下3个问题：满足各医院的最低药品需求；在满足最低药品需求的前提下，将尽可能多地药品运输到各个医院；总运费最小。

3.1 表上作业法求解

表上作业法常用的确定可行解的方法主要有3种：西北角法、最小元素法和最大差额法，其中最接近最优解的方法是最大差额法，最小元素法次之，效果最不好的是西北角法。本文主要采用最大差额法来确定可行解。

根据最大差额法，首先计算表1中每行与每列中2个最小元素之差，每行的差额从上往下依次是3、7、1，每列的差额从左往右依次是1、9、0、5。从每行和每列的数据中可以看出S2列的差额最大，为9，从该列中找出最小元素为11，即A2库存的药品首先满足S2的需求，因此A2仓库需要往S2运输80 t药品，由于S2的需求已经得到满足，因此将S2这列从单位运价表中划去，重复以上步骤，直到各个医院的药品需求得到满足为止。通过计算，得出的最优运输方案表如表2所示。

表2 运输方案表（单位：t）

根据表2最优运输方案是仓库1向医院3供货40 t，仓库1向医院4供货60 t，仓库2向医院2供货80 t，仓库2向医院3供货15 t，仓库3向医院1供货50 t，仓库3向医院4供货15 t。最低运费为4 020元。

3.2 Lingo求解

根据上文中所建立的数学模型，令X ij表示从公司仓库Ai到医院Sj运送的药品吨数，从而有以下运输问题的数学模型。

目标函数：MinZ=22*X11+20*X12…+25*X33+20*X34。

库存约束：∑X1j＜=100；∑X2j＜=95；∑X3j＜=110；j=1，2，3，4。

需求约束：∑Xi1=50；∑Xi2=80；∑Xi3=55；∑Xi4=75；i=1，2，3。

非负约束：Xij＞=0。

将建立的数学模型和已知的数据编写成Lingo语言，运用软件进行求解，用Lingo求解的过程如下所示：

单击Lingo软件工具条上的求解按钮，求解后得出的结果如图1所示。

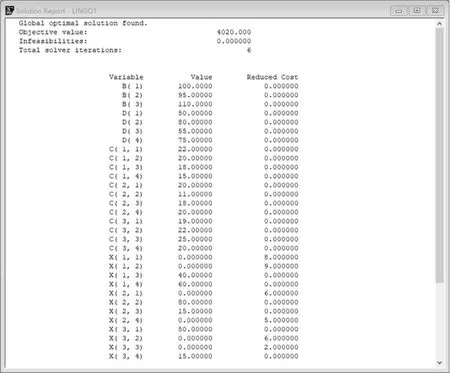
图1 Lingo求解结果

根据图1的结果显示最低运费为4 020元，最优运输方案是从仓库1向医院3供货40 t，从仓库1向医院4供货60 t，从仓库2向医院2供货80 t，从仓库2向医院3供货15 t，从仓库3向医院1供货50 t，从仓库3向医院4供货15 t。与3.1中表上作业法求解结果一致，由此可以得出文中所建立的数学模型具有一定的可行性，同时也体现了Lingo软件求解数学模型的快速与便捷，具有较高的可操作性。

4 结论

运输问题是一类特殊的数学规划问题，有着很实际的应用。随着物流的快速发展，会遇到越来越复杂的运输问题，通过Lingo软件，使得这些复杂问题的求解成为可能。本文在分析国内外运输方案发展情况的基础上提出以运费最小化为目标建立数学模型，通过编写Lingo程序语言求解，在实例中采用表上作业法和Lingo软件分别求解的方法，得出的计算结果一致，从而验证了所建立的数学模型的实用性与可行性，展示了Lingo软件在求解过程中的快速与便捷。当然，本文考虑是较为典型的运输问题，在日常生活中还会遇到其他特殊的情况，但不管怎样，通过软件求解是实践性较高的一种方法。