自振效应对平台式绝对重力仪影响的研究

王 栋冯金扬要佳敏吴书清王启宇胡 若李春剑

（中国计量科学研究院，北京100029）

1 引 言

重力加速度是一个随着时间的推移与空间的变化而变化的重力场参数，一般用表示，单位为m／s。 绝对重力测量是指对重力加速度绝对值的测量，测量结果普遍用毫伽（mGal，1mGal =1 ×10m／s）和微伽（μGal）表示。 绝对重力测量在计量学、资源勘探、地球物理、军事、惯性导航、海洋监测等诸多领域中有着重要意义。

绝对重力仪是实现绝对重力加速度精密测量的仪器，依照测量原理可分为激光干涉式绝对重力仪和原子干涉式绝对重力仪，目前其重力测量精度都达到了10量级。 当前大部分绝对重力仪采用激光干涉原理，在落体自由下落期间，通过激光干涉法精确测量其位置随时间的变化，最终拟合得到重力加速度值。

激光干涉式绝对重力仪存在很多的测量不确定度来源，其中一个重要的影响因素是仪器所受的振动。 目前对振动的处理方法主要有以下两种，一是使用隔振系统进行物理隔振；二是通过算法对振动进行补偿。 中国计量科学研究院自主研制的NIM 系列绝对重力仪采用振动补偿方法，在安静的实验室环境中测量不确定度为微伽量级，其中NIM-3A 型绝对重力仪曾参与2017年国际重力比对，表现良好。 为满足装备高精度动态导航定位以及海洋、太空等特殊环境重力测量的需求，发达国家都在大力发展平台式绝对重力仪，实现动态、实时绝对重力测量能力。 俄罗斯的A.Sokolov 等人以及我国的程冰等人均先后开展了平台式绝对重力仪的研究。

平台式绝对重力仪将干涉仪和真空筒三脚架固定在一个平台上，仪器的自振直接通过平台传到参考镜，自振影响被显著放大，会引入系统误差，因此提高平台式绝对重力仪测量精度的主要途径是降低振动的干扰。 由于平台式绝对重力仪参考棱镜处受到的振动扰动存在大量100Hz 以上的高频部分，而常用的速度型振动传感器带宽有限（通常小于70Hz），且传感器灵敏度过大会引发大振动条件下的信号溢出现象，导致振动补偿效果不佳，因此，需要对平台式绝对重力仪的振动特性进行深入研究，为平台式绝对重力仪的高精度测量提供保障。

本文在实验室环境下基于NIM-3C 型绝对重力仪，搭建了一套振动测量系统，通过加速度计研究了该系统工作时各位置的振动频谱特性并与分体式绝对重力仪进行了比较，同时对振动的传递率进行了分析，为提高平台式绝对重力仪的测量精度提供了支持。

2 仪器自振对重力测值的影响原理

2.1 NIM-3C 型绝对重力仪工作原理

NIM-3C 型绝对重力仪是将一个角锥棱镜作为落体在真空腔内做自由落体运动，用激光干涉法测量落体的下落距离，用原子钟同步的时钟信号测量对应的下落时间，对（，）数据对进行最小二乘拟合，再进行固体潮、气压、极移、仪器高等各项修正，得到被测点的重力加速度值，其原理如图1 所示。

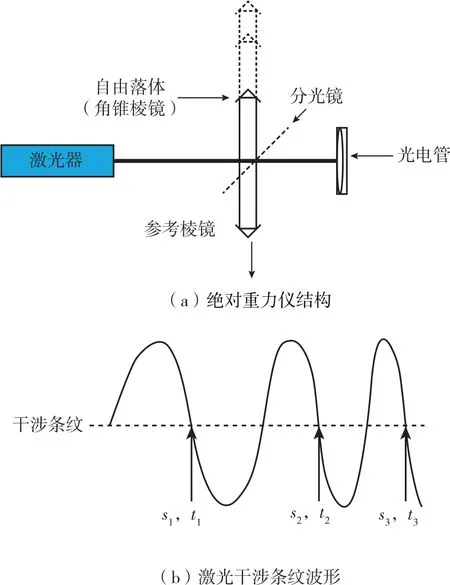
图1 绝对重力仪测量原理图Fig.1 Principle diagram of absolute gravimeter measurement

目前，影响绝对重力仪测量结果的一个主要因素是绝对重力仪工作时仪器自振对参考棱镜的扰动。 自振对测量位移的影响分析如下。

首先，系统由于受到反冲作用产生的自振会通过真空系统基座、地面、干涉仪基座，传递到干涉仪的参考棱镜上，使得参考棱镜受到扰动。 假设系统是时变线性系统，真空腔自振的振幅可表示为

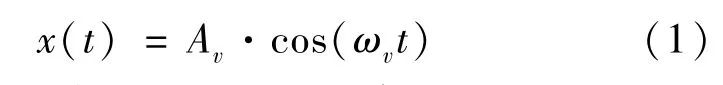
式中：A，ω——自振的振幅和频率。

振动传递函数的频域表达式为

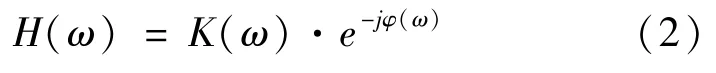
式中：（）——幅频；（）——相频函数。

参考棱镜受到的扰动可表示为

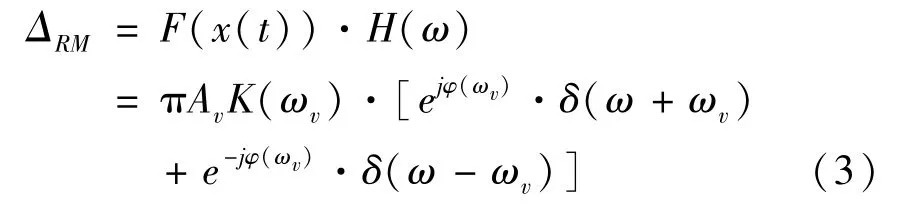
式中：（ω），（ω）——对应角频率为ω时的幅值传递率和相位差。

时域位移扰动可以表示为

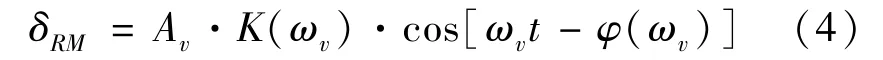
NIM-3C 型绝对重力仪采用地震计对参考棱镜处的振动进行采集，从而进行振动补偿，地震计可以准确测量的振动频段为DC ～70Hz。 这种振动补偿方法在现有实验室地基上效果良好，最终测量不确定度在10μGal 以内。 而NIM-3C 型绝对重力仪在平台式工况下，由于真空筒部分与干涉仪部分是直接相连的，所以振动的幅值被显著放大，频段也向高频迁移，如果直接沿用分体式的振动补偿方法，会带来mGal 量级的误差。

2.2 振动测量系统

分体式NIM-3C 的结构如图2 所示。

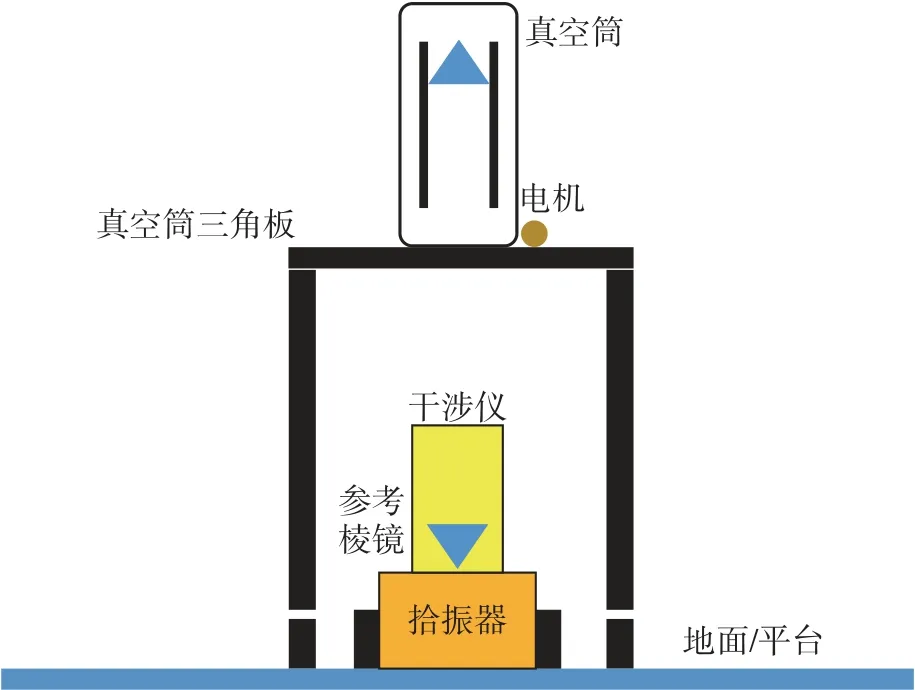
图2 NIM-3C 结构示意图Fig.2 Schematic diagram of the NIM-3C structure

引起测量误差的主要因素是电机工作时的振动以及真空筒内落体下落引起的振动，这些振动通过真空筒三角板向下传递到地面，再经由干涉仪地脚传递到干涉仪平面，最终传递到参考棱镜上。 记振动传递函数为

式中：a，a——输出和输入振动加速度。

振动由真空筒三角板传到地面的传递函数记为，由地面传到干涉仪地脚的传递函数记为，由干涉仪地脚传到干涉仪平面的传递函数记为，总的传递函数记为，可以得到

2.3 不同频率振动对重力测量值的影响

真空中自由下落的物体的运动轨迹可表示为理想的二次函数

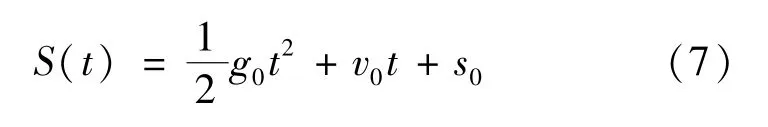
式中：——重力加速度；，——物体在自由落体时的初始速度和初始位置。

而通过激光干涉式绝对重力仪测得的运动轨迹为

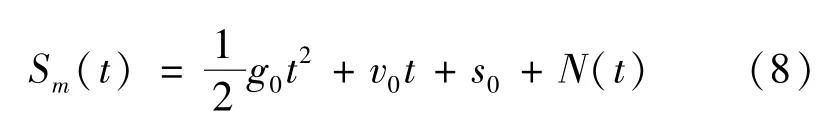
式中：（）——因参考棱镜的扰动而带来的误差。

因为其它影响量要小得多，因此可近似忽略。对（）进行二次拟合可得

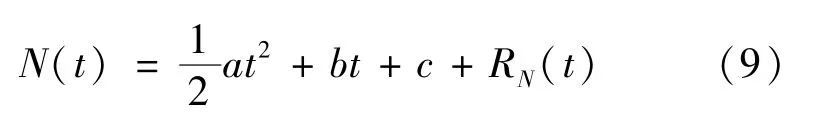
式中：，，——拟合系数；R（）——拟合残差。

因此，式（8）可化简为

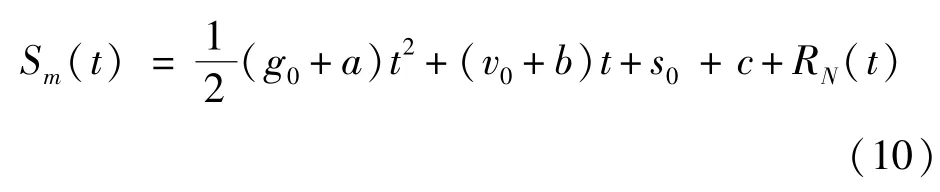
对激光干涉式绝对重力仪测得的运动轨迹直接二次拟合，得到的重力加速度值为

绝对重力仪带有对高频信号的衰减特性。而平台式工况下高频部分的振动特性比较复杂，因此有必要对振动频段进行限定。 本文根据实际测量数据确定了振动加速度的振幅，计算了在同等振幅情况下，不同振动频率对最终二次拟合重力加速度值的最大影响量。 在每个频率处都将振动的相位设定为对重力加速度值影响量的最大状态，如图3 所示。 可以看到，随着频率的增大，同等振幅条件下的振动对重力加速度值的影响量迅速减小，在400Hz 处降到10μGal 量级。 对于当前测量精度要求，400Hz 之后的振动可以忽略。

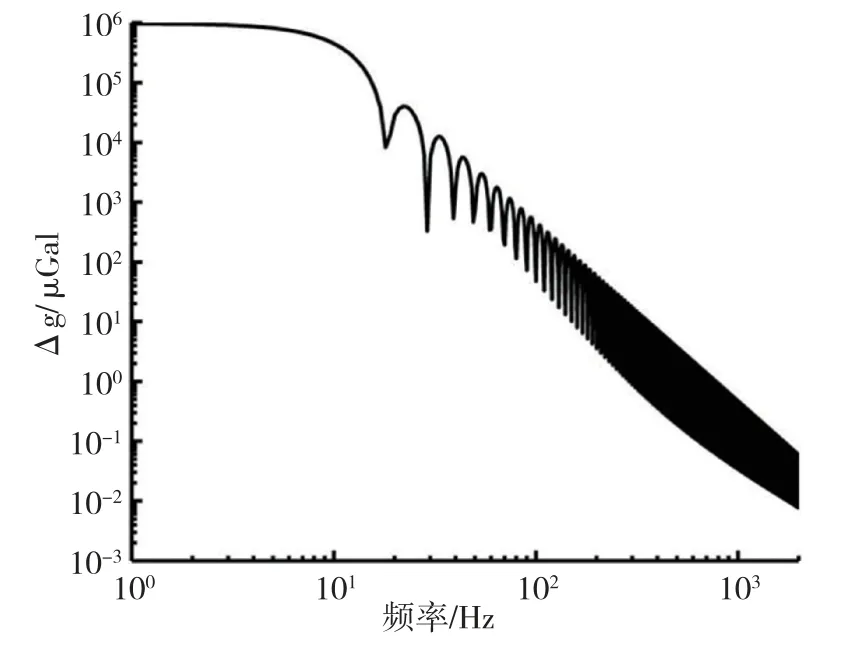
图3 不同频率振动对重力测量值的影响图Fig.3 The influence of different frequency vibrations on the measured value of gravity

3 重力仪自振测试实验

实验系统主要由NIM-3C 型绝对重力仪、铝制平台、单轴加速度传感器（MSA1000A-02，以下简称MEMS 加速度计）、 云智慧数据采集分析仪（INV3062-C1）组成，如图4 所示。 MEMS 加速度计量程为±2g（g =9.8m／s），带宽为（10～2 000）Hz，灵敏度为1 026.3mV／g。

图4 自振测试实验工况图Fig.4 Working condition diagram of self-vibration test

实验分为两个阶段，首先是对分体式NIM-3C的振动采集。 将分体式NIM-3C 调试到最佳状态后，将MEMS 加速度计固定在振动传递路径上，将真空筒三角板、地脚旁边的地面、干涉仪地脚上、干涉仪平面的加速度计信号依次接入3062C 振动采集盒的通道1、通道2、通道3 和通道4 中，然后通过手动触发使真空筒中的落体开始自由下落，同时使用Dasp V 软件采集4 个通道的振动数据，时长1min，重复10 组。 对于分体式和平台式工况下真空筒三角板处的振动，10 组1min 的数据重复性良好，如图5 所示。

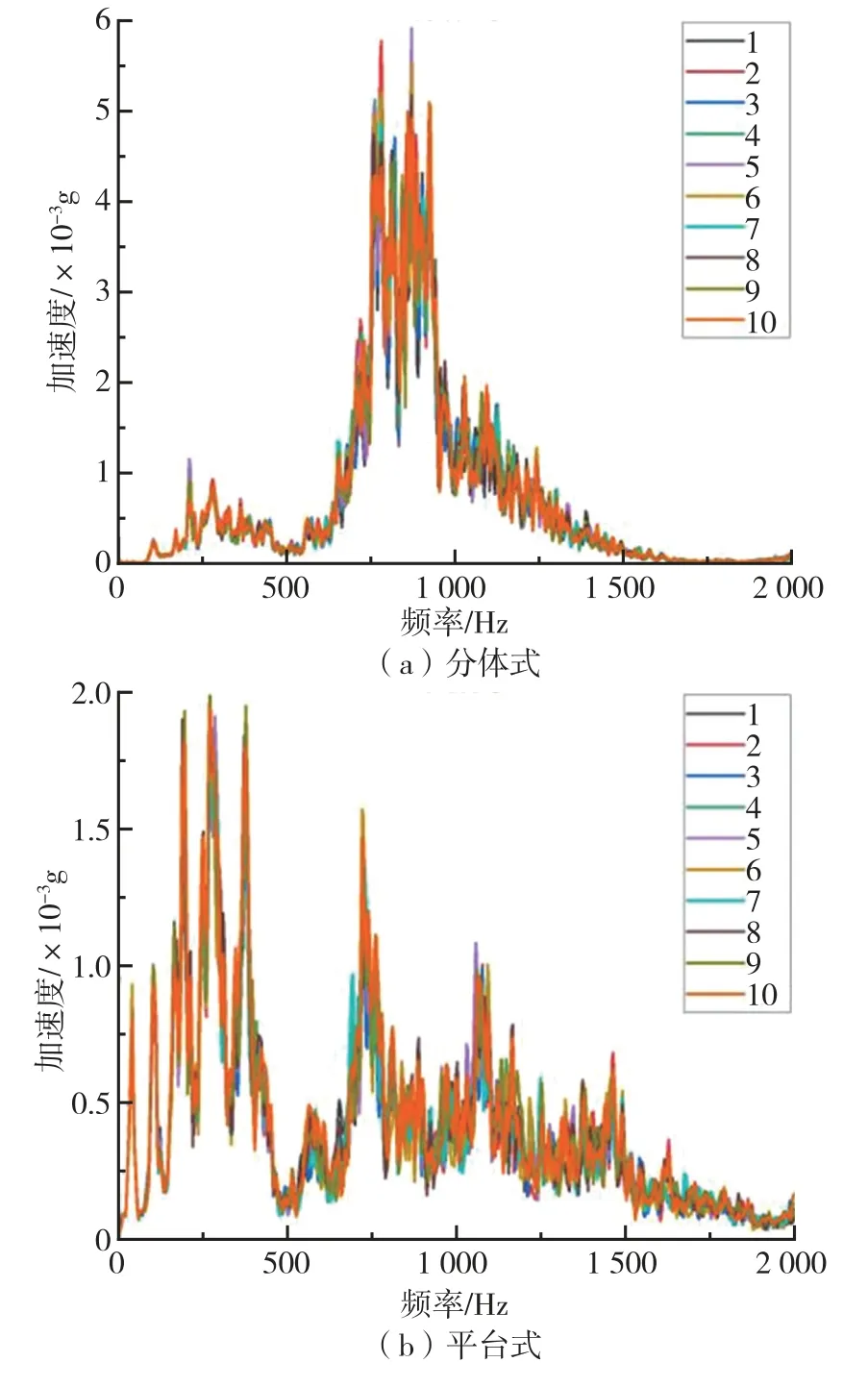
图5 振动采集重复性结果图Fig.5 Results of vibration collection repeatability

NIM-3C 平台式工况下的振动采集与分体式相仿，只是将2 号位置的加速度计从地面移动到铝制平板上，此处不再赘述。

4 重力仪自振测试结果

在真空筒三角板处，分体式工况与平台式工况的振动情况如图6 所示。 图6（a）为加速度计能测到的2 000Hz 以下的振动，从图中可以看出，由于结构与整体质量的不同，分体式工况下的振动主频主要集中在（500～1 500）Hz 之间，而平台式工况的振动主频主要集中在0～500Hz 之间；图6（b）为振动对应的对重力加速度测量值的影响量，由于1 000Hz之后的影响量只有μGal 量级，因此忽略不计。 如右图所示，在500Hz 以上的频段，分体式工况存在最大10μGal 量级的影响量，略高于平台式工况。 而在300Hz 以下的频段存在100μGal 甚至mGal 量级的影响，并且对平台式工况的影响量远大于分体式工况。

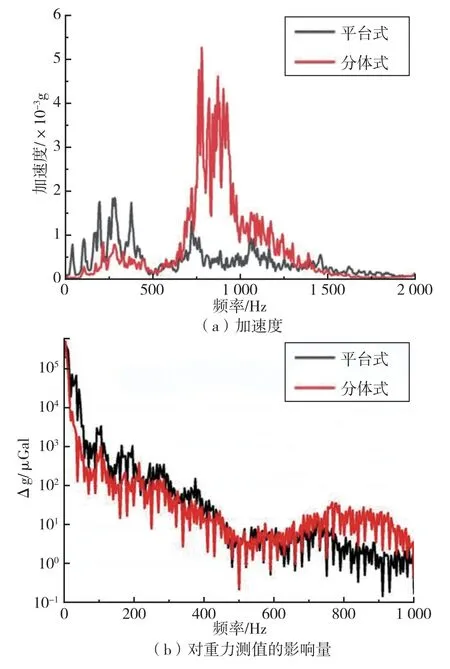
图6 真空筒三角板处振动对比结果图Fig.6 Vibration comparison results of vacuum cylinder support

在干涉仪平面处，分体式工况与平台式工况的振动情况如图7（a）所示。 分体式工况中真空筒的振动可以被隔振地基大幅度的衰减，而平台式工况由于干涉仪部分和真空筒直接相连，所以其所受振动的振幅远大于分体式工况，同时包含很多振动主频。 振动对应的对重力加速度测量值的影响量如图7（b）所示，400Hz 以上的频率对重力加速度测量值的影响量只有μGal 量级，可以忽略不计。 同时平台式工况受振动的影响量远大于分体式工况。

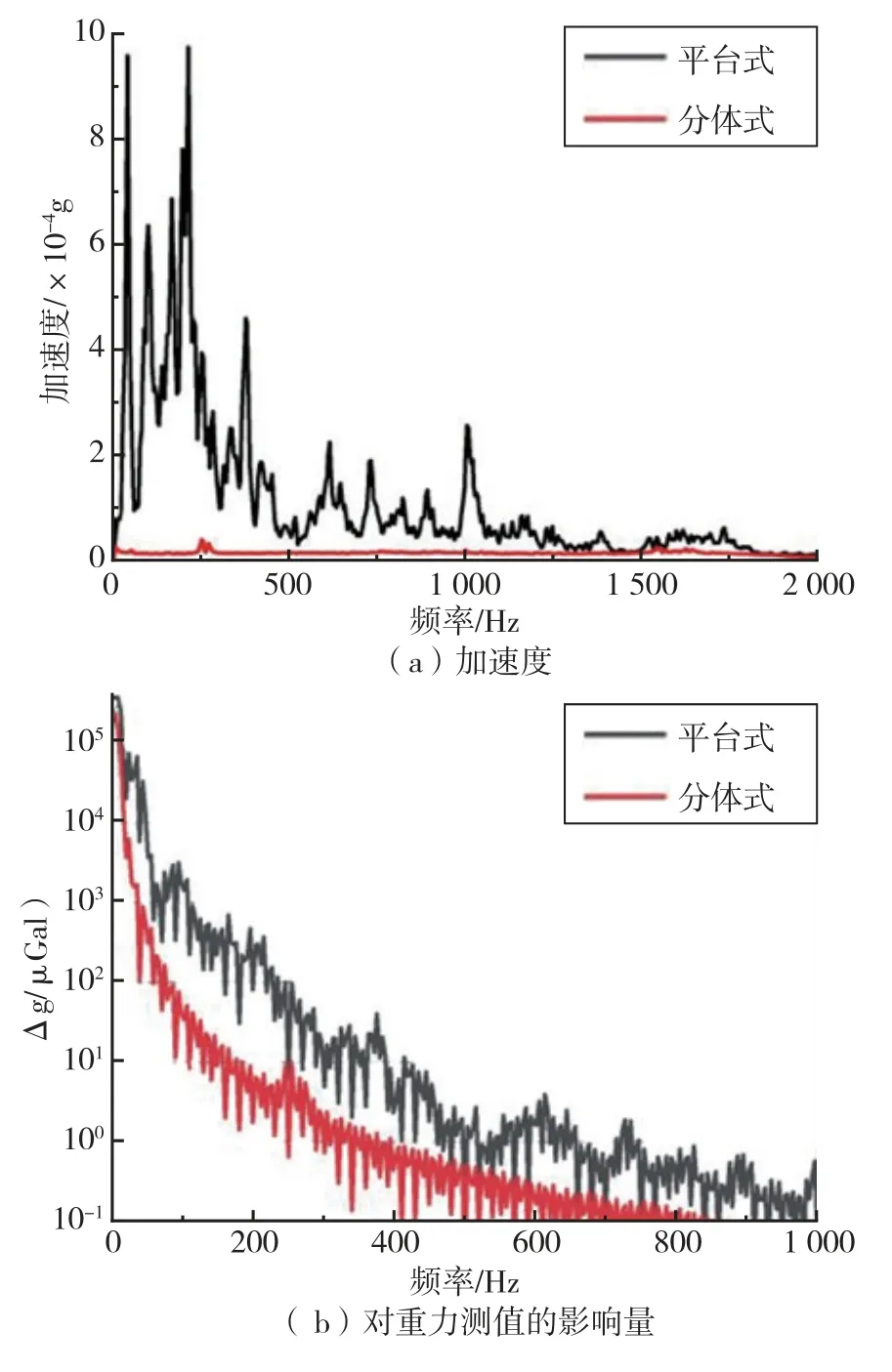
图7 干涉仪处振动对比结果图Fig.7 Vibration comparison results of the interferometer

分体式和平台式的振动从真空筒三角板到干涉仪处的总传递函数如图8 所示。 由图可见，分体式的结构对于100Hz 以上的高频振动有很强的衰减能力，而低频部分虽然有部分振动可以传递过去，但是大部分都在现有拾振器的测量范围内，因此现有的振动补偿方式可以起到相对不错的补偿效果。 而对于平台式工况，全频段的传递率均高于分体式工况，同时在70Hz 以上的高频段也有几个对振动放大的成分，因此无法直接沿用现有的振动补偿方案。

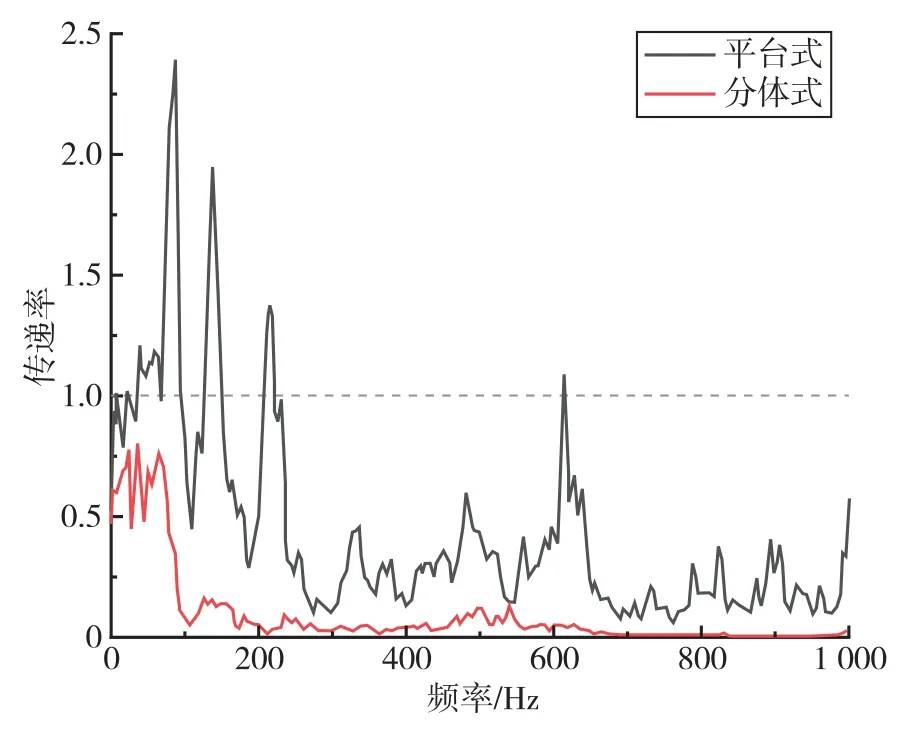
图8 平台式与分体式传递率比较图Fig.8 Comparison of transmission rate between platform type and split type

为进一步分析平台式工况下的振动传递过程，本文将平台式NIM-3C 的振动传递路径拆分为三段，分别为真空筒三角板到铝制平台、铝制平台到干涉仪地脚、干涉仪地脚到干涉仪平面，并计算了每段传递路径的传递函数··，与干涉仪所受振动如图9 所示。

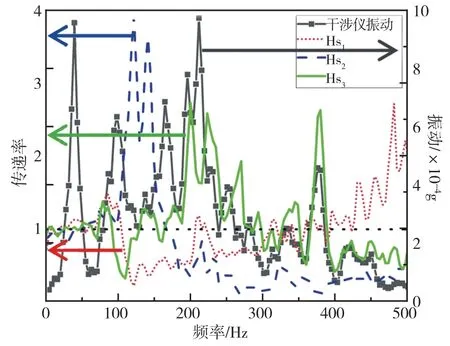
图9 平台式工况干涉仪振动与各段的传递率Fig.9 The vibration of the platform-type working condition interferometer and the transmission rate of each section

干涉仪所受振动主要有五个峰值，分别发生在39Hz，98Hz，164Hz，190Hz ～210Hz，375Hz 频段。 其中前两个峰值并没有被某一个环节明显放大，三个传递路径的传递率都很接近，第三个峰值主要由以及共同放大引起，第四与第五个峰值则主要由单独放大引起。 综上所述，有效降低的振动传递率对解决平台式NIM-3C 工况下的振动问题至关重要。

5 结束语

本文建立了NIM-3C 型绝对重力仪的振动传递模型并搭建了振动测量系统，通过MEMS 加速度传感器监测了NIM-3C 型绝对重力仪在分体式以及平台式工况下工作时的振动数据并对振动数据进行了处理和分析，同时对振动可能造成的重力加速度测量值的影响进行了评估。 通过对振动传递函数的计算和分析，最终找到了减小平台式NIM-3C 型绝对重力仪干涉仪所受振动的关键环节。 通过上述工作，可以为提高平台式NIM-3C 型绝对重力仪的测量精度提供支撑。

针对平台式NIM-3C 型绝对重力仪振动超出现有拾振器量程的问题，下一步可以尝试使用带宽更宽的高精度加速度计，如titan 加速度计（带宽DC-430Hz）来对高频部分进行振动的采集与补偿，或者加入被动隔振材料，如金属橡胶隔振地脚或者橡胶垫来降低振动的幅值，将振动向低频段迁移。