方位弹性阻抗傅里叶级数裂缝预测方法
2022-04-11刘晓晶陈祖庆肖秋红
刘晓晶 陈祖庆 陈 超 肖秋红
(中国石油化工股份有限公司勘探分公司物探研究院, 四川成都 610041)
0 引言
郭旭升等[1-2]研究涪陵气田焦石坝、平桥地区五峰组—龙马溪组页岩后认为,裂缝是影响页岩气产能的关键因素。随着页岩气勘探向深层领域迈进,页岩储层裂缝对工程压裂的积极作用逐渐体现。天然裂缝具有良好的结构弱面,强度较低,导致存在天然裂缝的地层更易于压裂,是影响压裂效果的关键因素[3]之一。因此,高精度裂缝预测在页岩气勘探中具有重要意义。在地震数据处理中每一个炮检距向量片(Offset Vector Tile,OVT)都有自己的方位角信息,偏移后能够保留方位角信息。因此,OVT地震道集资料在叠前各向异性裂缝预测中具有明显优势[4-6],为高精度裂缝预测奠定了良好的数据基础[7-9]。
Hudson[10-11]、Thomsen[12]认为,含裂缝地层具有明显的各向异性特征,基于方位各向异性的裂缝预测已经成为当前的主流技术。目前的裂缝预测方法主要分为两类。第一类方法基于方位地震数据的振幅或振幅导出属性(频率、衰减等)预测裂缝。Mallick等[13]认为,反射振幅随方位的变化曲线大致是一条周期为π的余弦曲线,可据此预测裂缝。Rüger[14]建立了HTI介质方位AVO反射系数近似方程,为各向异性研究奠定了基础。Al-Marzong等[15]在极坐标系下将不同方位的AVO梯度随观测方位的变化关系拟合为椭圆,并利用椭圆率表征裂缝发育密度,椭圆长轴指示裂缝走向。Downton等[16-18]利用傅里叶级数展开Rüger的方位AVO反射系数近似方程,根据二阶傅里叶系数预测裂缝。印兴耀等[19]基于叠前方位道集,利用各向异性梯度反演方法预测裂缝。王康宁等[20]对比了傅里叶级数与椭圆展开法,认为二者预测结果等价。第一类方法得到的裂缝各向异性信息实际是界面两侧地层裂缝信息的综合响应,无法确定上覆、下伏地层的裂缝信息。第二类方法基于方位AVO叠前地震反演获得不同方位的弹性参数,进而利用椭圆拟合法预测裂缝,或者直接反演各向异性参数。王建花等[21]利用方位杨氏模量椭圆拟合预测裂缝。陈怀震[22]、Pan 等[23]基于岩石物理模型驱动研究了各向异性参数反演,并取得一定效果。第二类方法可直接求取目的层内的裂缝信息,在理论上精度更高。虽然宽方位地震勘探已成为现阶段地震勘探技术发展的主流方向之一,为方位AVO叠前反演提供了高品质的五维道集资料[5],但待反演参数维度高(一般为5~6个),且各向异性参数值较弹性参数值小得多,反演稳定性有待提升。
第一类方法仅能得到界面两侧地层的综合响应,无法确定上覆、下伏地层的裂缝信息,影响实际勘探评价,精度偏低。为此,本文基于Rüger的方位AVO反射系数近似方程[14],首先推导了方位弹性阻抗方程,将裂缝介质的界面信息转化为地层内部的弹性信息,方位弹性阻抗差异体现了地层的各向异性。其次,利用傅里叶级数展开方位弹性阻抗方程求取二阶傅里叶系数,通过方位弹性阻抗与余弦函数的互相关求取裂缝法向。最后,通过模型验证方法的有效性与抗噪性,利用川东南DS-DX地区页岩气实际资料验证方法的精度,并利用裂缝预测结果简单评估压裂施工情况。
1 方位弹性阻抗方程傅里叶级数展开
在HTI介质中,非零入射角的不同方位地震波速度存在差异,因此地震振幅随方位变化。Rüger[14]根据一阶扰动理论给出了HTI介质方位反射系数近似方程
[Δδ(v)+8gΔγ]cos2φ}sin2θ+
Δδ(v)sin2φcos2φ]sin2θtan2θ
(1)

Downton等[16]利用傅里叶级数展开式(1),并利用二阶傅里叶系数预测裂缝
R(θ,φ)=r0+r2(θ)cos2φ+r4(θ)cos4φ
(2)
式中r0、r2、r4分别为基于反射系数的零阶、二阶、四阶傅里叶系数。
基于式(2)的裂缝预测结果是界面两侧介质的综合响应,无法确定上覆、下伏地层的裂缝信息。为了消除这种不确定性,首先根据Connolly[24]与Whitcombe[25]建立弹性阻抗的思想,将式(1)转换为方位弹性阻抗方程
exp[ε(v)cos4φsin2θtan2θ]×
exp[sin2θcos2φ(1+tan2θsin2φ)×
δ(v)]×exp(4gγsin2θcos2φ)
(3)
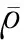
由于式(3)是非线性的,为了方便求解,进一步对其线性化处理。首先令
(4)
将式(3)等式两端同时除以A(θ),并令EIA(θ,φ)=AEI(θ,φ)/A(θ),再对等式两边取对数,即可得到线性化方位弹性阻抗方程
lnEIA(θ,φ)=sec2θlnVP-8gsin2θlnVS+
(1-4gsin2θ)lnρ+ε(v)cos4φsin2θtan2θ+
δ(v)sin2θcos2φ(1+sin2φtan2θ)+
4gγsin2θcos2φ
(5)
由于裂缝的各向异性特征与方位有关,且式(5)中的方位信息均为三角函数幂的形式。通过傅里叶级数展开,进而可以得到方位弹性阻抗的傅里叶级数展开式
ln[EIA(θ,φ)]=A0+A2cos2φ+A4cos4φ
(6)
其中
A0=sec2θlnVP-8gsin2θlnVS+
(7)
(8)
(9)
式中:A0为基于方位弹性阻抗的零阶傅里叶系数,为背景项,与观测方位无关,包含弱各向异性信息;A2与A4分别为基于方位弹性阻抗的二阶与四阶傅里叶系数,只与入射角和各向异性参数有关,反映了裂缝的各向异性特征。通常θ<30°,则sin2θtan2θ≈0,A4≈0。
根据川东南地区五峰组—龙马溪组页岩特征设计了两层模型(表1)分析式(6)的精度(图1)。可见:二阶项随方位呈周期性变化明显,四阶项接近于0,且四阶项幅值远小于二阶项(图1a); 式(6)取三项与前两项的曲线几乎重合(图1b),因此第三项A4cos4φ可以忽略。
上述分析表明,式(6)可以简化为
ln[EIA(θ,φ)]≈A0+A2cos2φ
(10)
其中
(11)
根据各向异性参数与裂缝密度的关系[26]
(12)
(13)
将式(12)、式(13)代入式(11),得
(14)
式中e为裂缝密度。

表1 两层介质模型参数
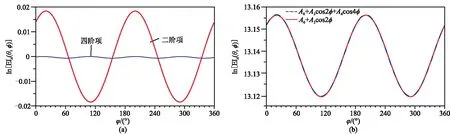
图1 式(6)精度分析(a)二阶项与四阶项; (b)两项与三项展开
由式(14)可知:θ越大,|A2|越大,因此通常使用较大入射角的地震数据预测裂缝; 当θ一定时,|A2|与e成正比,因此|A2|反映了裂缝密度。
2 傅里叶系数提取与裂缝面法向预测
准确求取傅里叶系数与裂缝面法向即可准确预测裂缝。将φ=φ-φN代入式(10),得
ln[EIA(θ,φ)]≈A0+A2cos2φNcos2φ+
A2sin2φNsin2φ
(15)
待求的φN不随观测方位变化,可以视为常数,因此可以将A2cos2φN、A2sin2φN分别视为cos2φ、sin2φ的系数。由于正弦函数与余弦函数均具有正交性,因此对于N个方位弹性阻抗即可利用
(16)
(17)
(18)
(19)
快速求取A2与φN,式中Δφ为观测方位角的变化量。然而,Downton等[16]指出,由于arctan函数的值域为[0,180°],利用式(19)得到的φN的值域为[0,90°],当实际裂缝面的φN大于90°时,则无法准确预测φN。为此,Ma等[27]提出利用成像测井裂缝方位信息进行约束,可以解决井点附近裂缝方位预测不准的问题,但对于远离井点的位置,可能存在较大预测误差。
由式(10)可见,ln[EIA(θ,φ)]随φ的变化由cos2φ控制,通过求取ln[EIA(θ,φ)]与cos2φ的互相关系数求取φN,即将cos2φ从左向右平移φN后,计算cos2φ与ln[EIA(θ,φ)]的相关系数
(20)
为了准确预测裂缝面法向,进一步利用表1数据分析式(10),寻求准确的预测裂缝方法。图2为ln[EIA(θ,φ)]与cos2φ的互相关分析,由图可见:①ln[EIA(θ,φ)]随φ的变化曲线(图2a)与cos2φ随φ的变化曲线(图2b蓝线)具有明显的相关性,且存在一定相位差。②当φ=20°(平行裂缝面)时,ln[EIA(θ,φ)]最大,随着φ逐渐增大,ln[EIA(θ,φ)]逐渐减小,当φ=110°(垂直裂缝面)时,ln[EIA(θ,φ)]达到最小(图2a)。③将cos2φ从φ=0°开始向右平移,当φ=20°时,cos[2(φ-20π/180)](图2b蓝线)与ln[EIA(θ,φ)]形态一致,RE(φN)达到最大(图2c); cos2φ再向右平移,RE(φN)逐渐减小直至负值,当φ=110°(垂直裂缝面)时(图2b红线),RE(φN)达到最小,且RE(φN)曲线呈周期性变化,周期为π(图2c)。因此只需找出一个周期内RE(φN)最小时对应的平移角度φN,即可确定裂缝面的法向
cos[2(φi-φN)]}
(21)
根据上述分析建立了基于方位弹性阻抗傅里叶级数的裂缝预测流程(图3)。首先,将方位叠前地震道集划分为N个方位道集,将每个方位道集分为小、中、大入射角地震数据并进行部分叠加; 其次,对N个方位的大入射角地震数据开展系数脉冲反演得到N个大入射角弹性阻抗数据体; 然后,将N个方位弹性阻抗数据体除以A(θ)并取对数,进而利用式(15)~式(18)求取A2表征裂缝密度; 最后,利用互相关方法求取裂缝法向,进而准确预测裂缝。
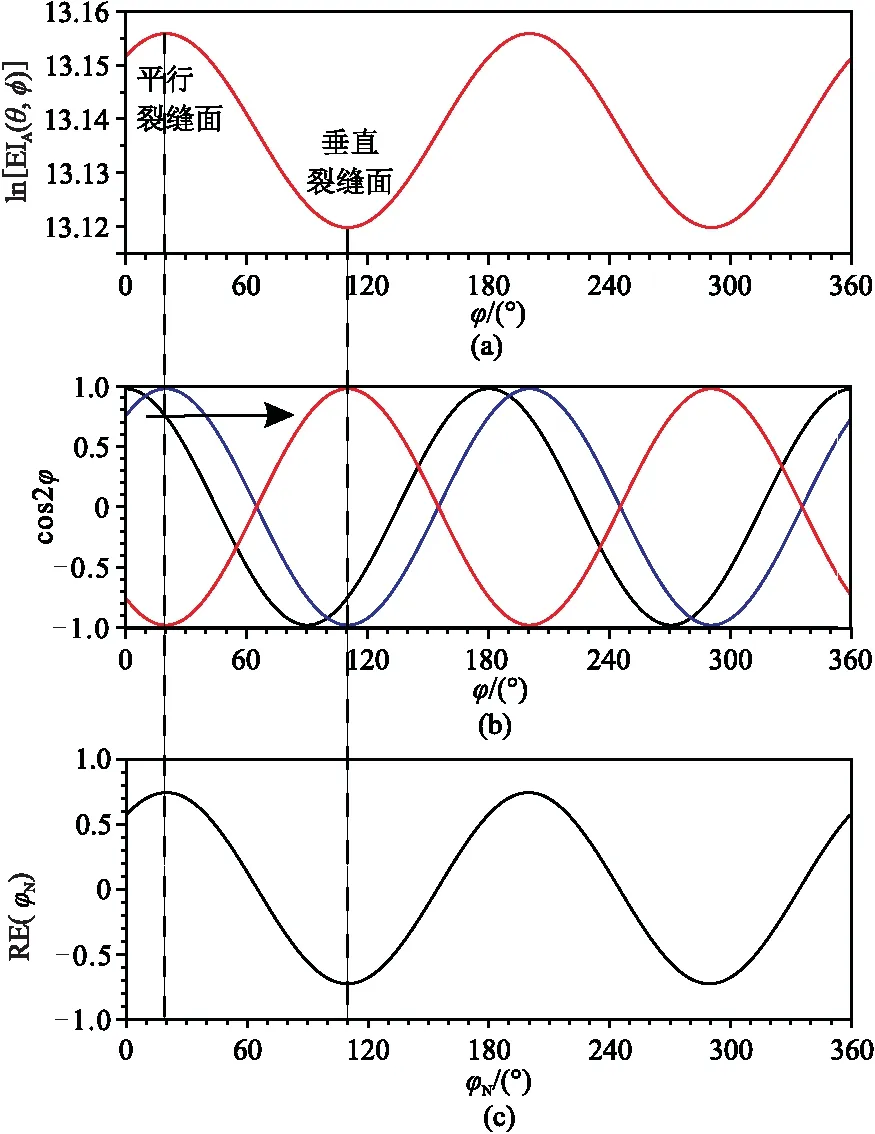
图2 ln[EIA(θ,φ)]与cos2φ互相关分析(a)ln[EIA(θ,φ)]随φ变化曲线;(b)cos2φ随φ变化曲线;(c)RE(φN)随φN变化曲线

图3 基于方位弹性阻抗傅里叶级数的裂缝预测流程
3 模型测试
为了验证方法的有效性,设计了四层模型(表2),利用40Hz的雷克子波作为震源进行正演,得到θ=30°的方位地震道集(图4a),基于地震数据的傅里叶级数展开预测裂缝(图4)。可见,各界面的振幅随φ的变化曲线(图4c~图4e)清晰地展示了各向异性特征,但直接利用振幅的预测结果只能反映界面的各向异性特征(图4b箭头处),无法反映地层的裂缝发育特征(图4b红色虚线框与实线框分别指示第1层、第3层),无法确定上覆、下伏地层的裂缝信息。
图5为无噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果。由图可见:①θ=30°的方位弹性阻抗(图5a)清晰地展示了第1层与第3层的弹性阻抗随φ的变化。②A2(图5b)指示第1层与第3层的裂缝发育强度一致,第2层与第4层裂缝不发育。③常规方法(图5c)得到的第1层的φN准确(与模型一致),第3层的φN不准确(35°,与模型相差90°)。④本文方法得到的第1层与第3层的φN较准确(图5d)。由于受噪声影响,通常不能得到精确的方位弹性阻抗。图6为含噪声(信噪比为40)时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果,由图可见,裂缝预测结果与不含噪声时一致。
进一步在方位弹性阻抗中加入不同强度的噪声(信噪比分别为20、10),分别得到基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(图7、图8)。可见,由于方位弹性阻抗受噪声影响较大,随着噪声强度增加对裂缝预测结果的影响也增大(图8),但仍能清楚地指示第1层与第3层的裂缝发育特征,预测的φN抖动剧烈,但裂缝预测结果与不含噪声时基本一致。
模型测试表明,基于方位弹性阻抗傅里叶级数展开的裂缝预测方法能较好地预测裂缝发育情况以及裂缝法向,精度较高且抗噪性较强。
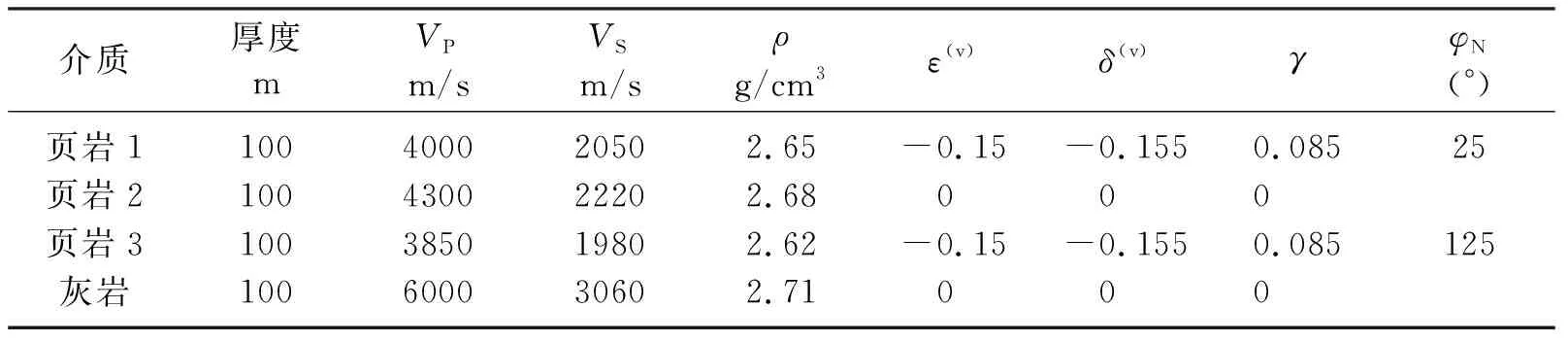
表2 四层介质模型参数

图4 基于地震数据的傅里叶级数展开裂缝预测结果(a)θ=30°的方位道集合成记录; (b)r2; (c)界面1振幅随φ变化曲线; (d)界面2振幅随φ变化曲线; (e)界面3振幅随φ变化曲线
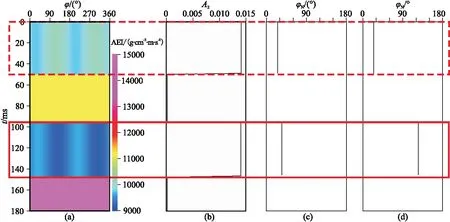
图5 无噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(a)θ=30°方位弹性阻抗; (b)A2; (c)常规方法的φN; (d)本文方法的φN
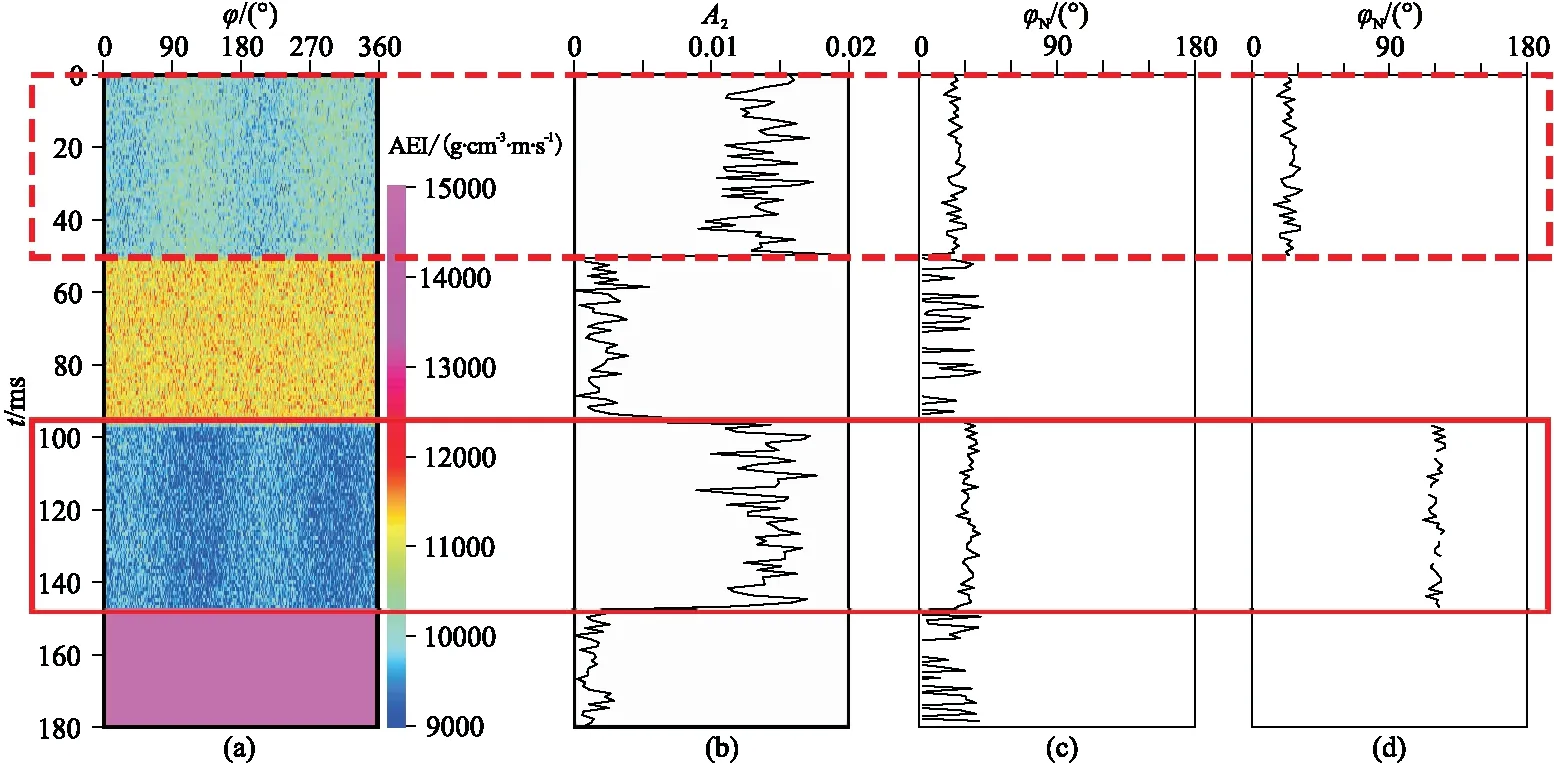
图6 含噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(信噪比为40)(a)θ=30°方位弹性阻抗; (b)A2; (c)常规方法的φN; (d)本文方法的φN
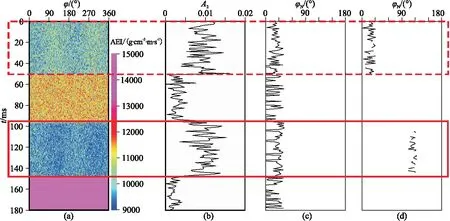
图7 含噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(信噪比为20)(a)θ=30°方位弹性阻抗; (b)A2; (c)常规方法的φN; (d)本文方法的φN
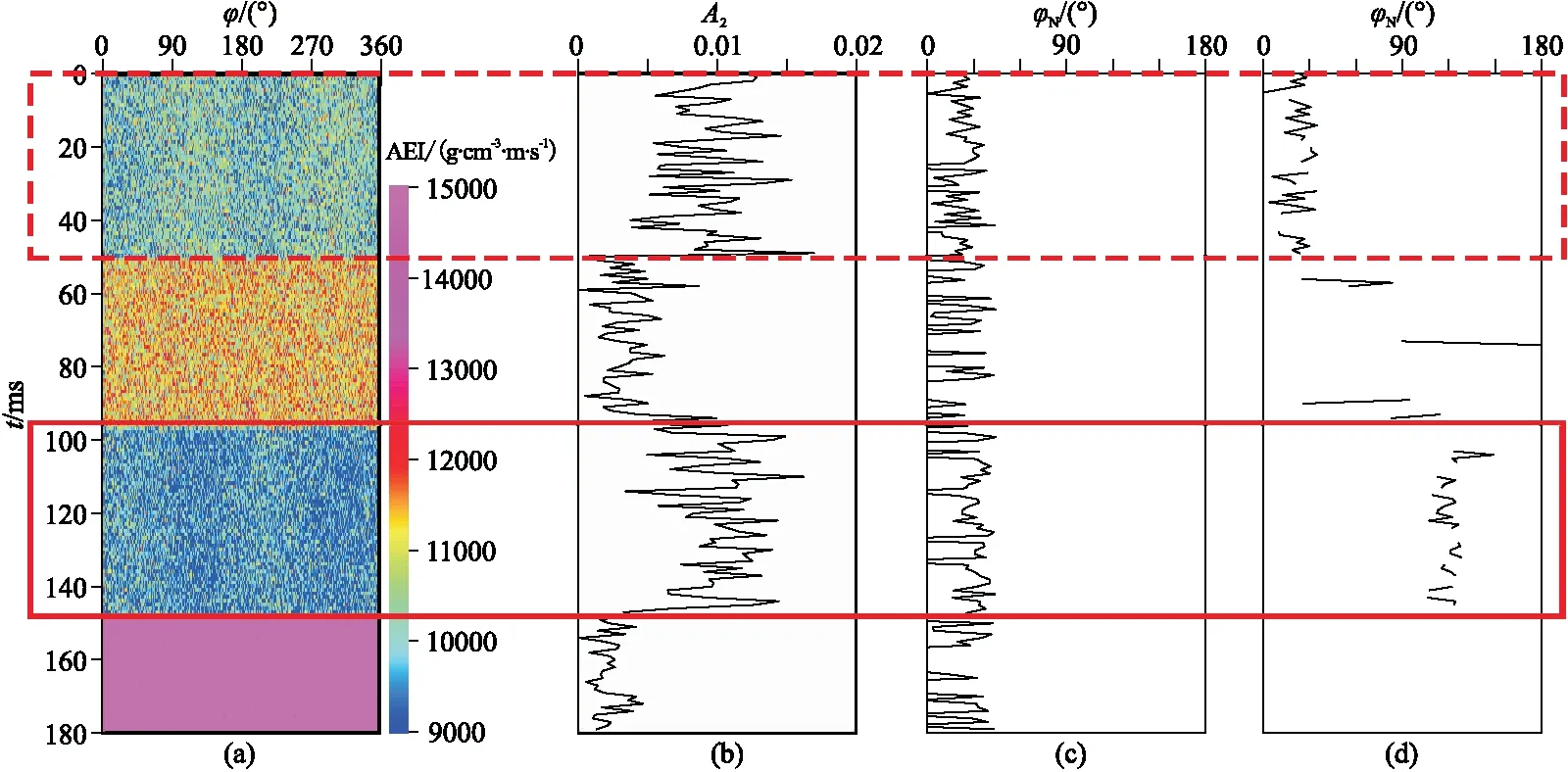
图8 含噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(信噪比为10)(a)θ=30°方位弹性阻抗; (b)A2; (c)常规方法的φN; (d)本文方法的φN
4 实际资料应用
4.1 预测精度对比
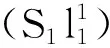

图9 DY4岩心
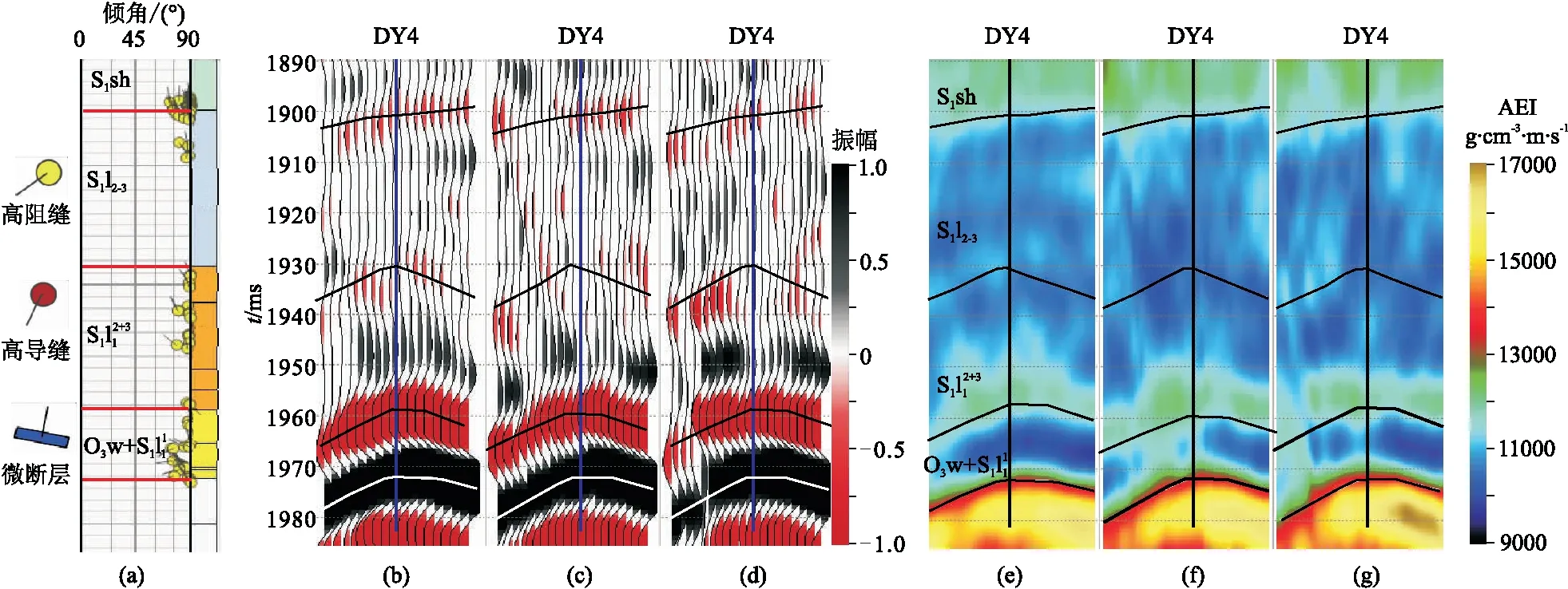
图10 DY4井成像测井、DY4井旁大入射角不同方位地震、弹性阻抗数据对比(a)成像测井; (b)、(c)、(d)入射角27°时,方位角分别为0°~30°、30°~60°、60°~90°的部分叠加剖面;(e)、(f)、(g)入射角27°时,方位角分别为0°~30°、30°~60°、60°~90°的方位弹性阻抗反演剖面



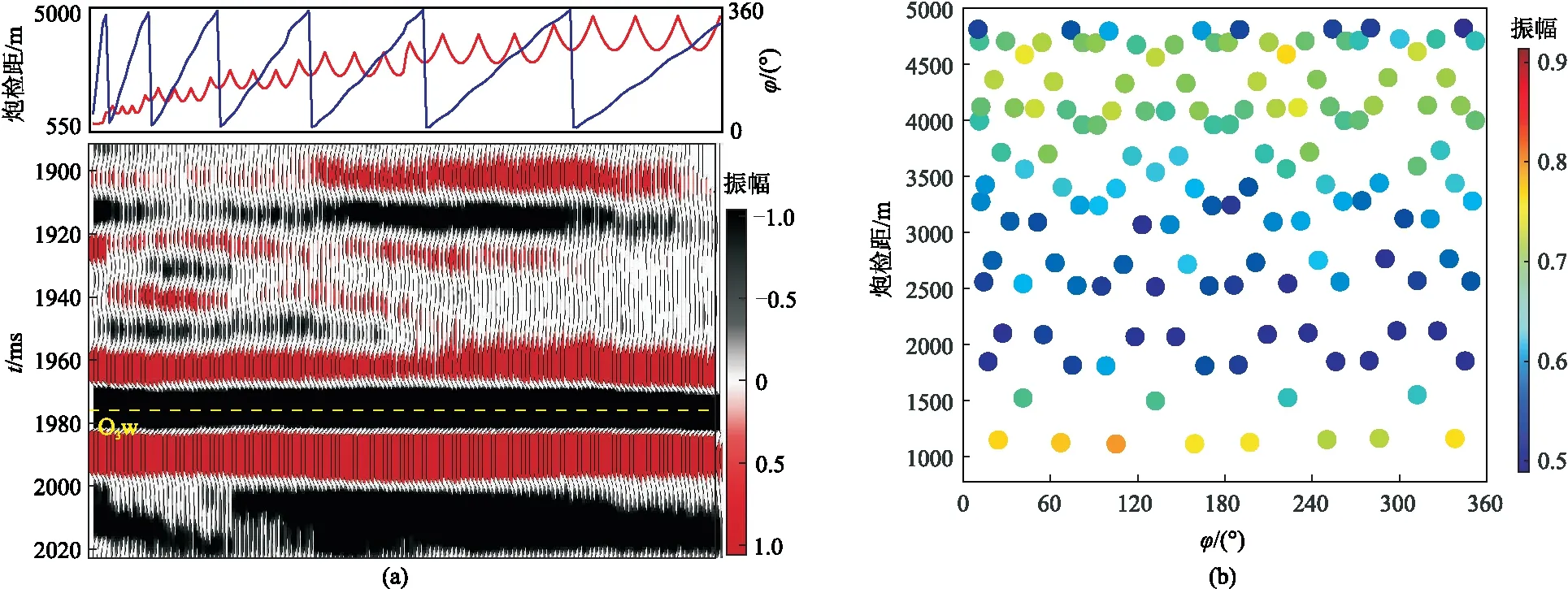
图11 井旁道OVT叠前道集(a)以及目的层均方根振幅随方位角变化(b)图a中红色曲线为炮检距变化曲线,蓝色曲线为方位角变化曲线,黑色虚线为五峰组底界(O3w)
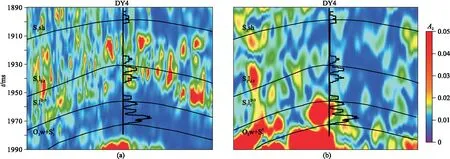
图12 DY4井裂缝密度预测剖面(a)基于方位振幅; (b)基于方位弹性阻抗(图10e~图10g)黑色曲线为成像测井数据得到的裂缝密度曲线
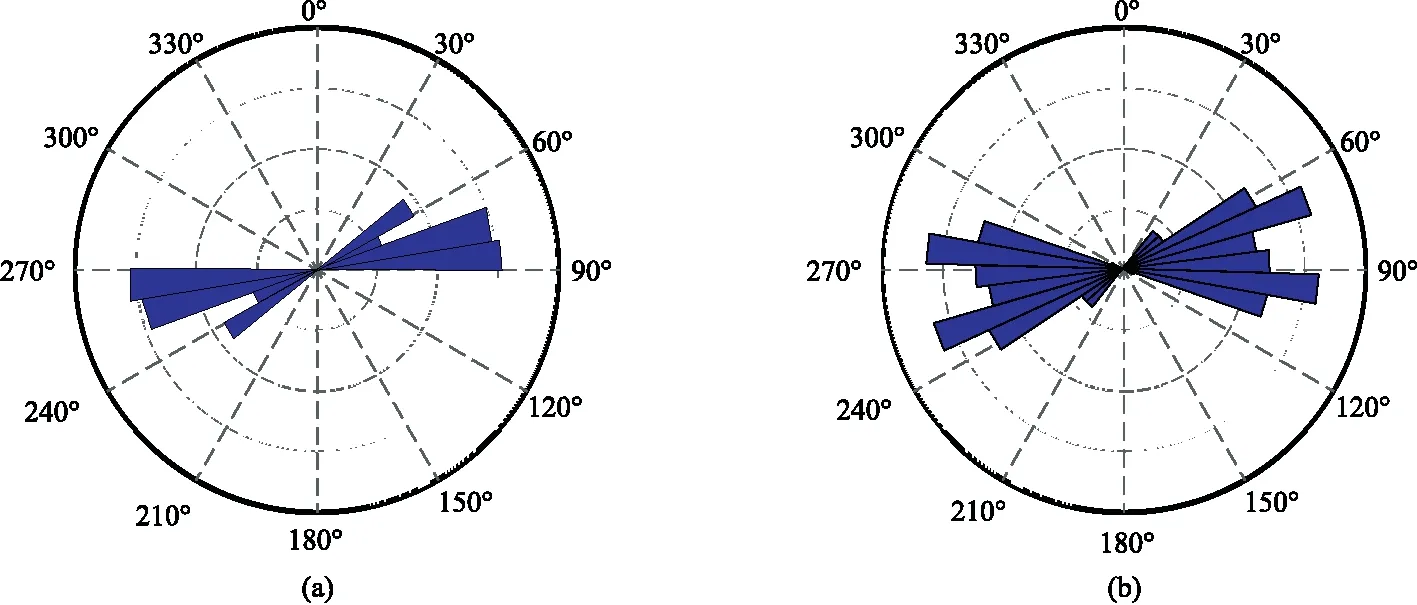
图13 DY4井实测裂缝走向(a)与预测裂缝走向(b)
4.2 预测结果应用
页岩气勘探逐渐走向深层领域(埋深大于4000m),地应力增加,地层压裂难度增加,施工难度较大。若地层中裂缝发育,地层更容易破裂,降低了压裂施工的破裂压力。图14为DS-DX地区过DYS1HF井裂缝预测剖面。由图可见,水平井轨迹在优质页岩层段穿行,其中1~9段以及20~26段裂缝密度较低,中部10~19段裂缝较发育。DYS1HF井区预测裂缝平面分布图(图15)同样表明DYS1HF井10~19段裂缝较发育。图16为DYS1HF井3~26段破裂压力直方图。对比图14、图15与图16发现,裂缝发育段(11~19段)地层破裂压力相对其他段较低(图16),其中14~16段裂缝密度最大(图15),破裂压力最低。DYS1HF井破裂压力与A2交会分析表明,裂缝密度与破裂压力呈负相关,即裂缝越发育,破裂压力越低(图17)。因此,本文提出的裂缝预测方法精度较高,裂缝预测结果可为页岩气井位部署、水平井设计等提供可靠的参考依据。
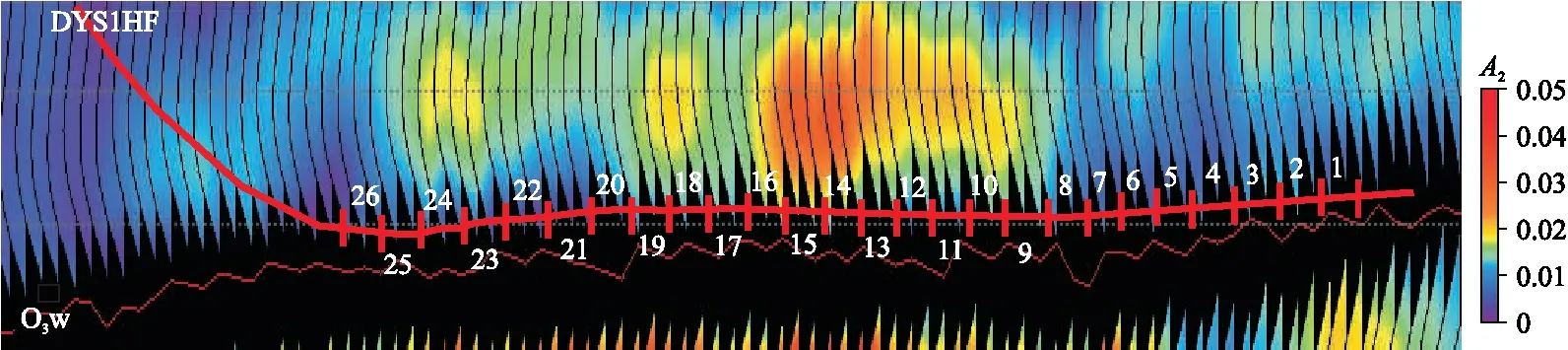
图14 DS-DX地区过DYS1HF井裂缝预测剖面
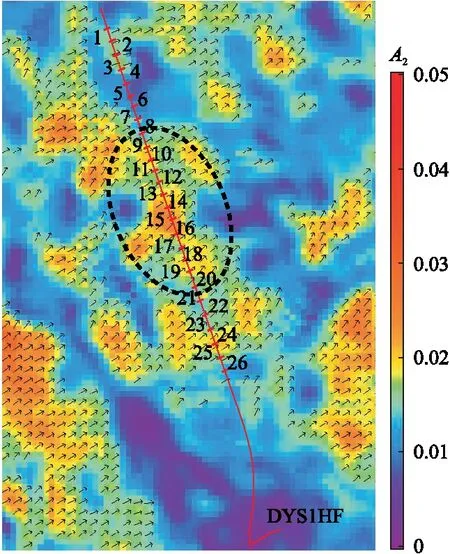
图15 DYS1HF井区预测裂缝平面分布图

图16 DYS1HF井3~26段破裂压力直方图

图17 DYS1HF井破裂压力与A2交会图
5 结论
文中提出了基于方位弹性阻抗傅里叶级数展开的裂缝预测方法。首先通过方程推导建立方位弹性阻抗方程,将地震界面各向异性信息转化为地层内部各向异性信息,进而对方位弹性方程进行傅里叶级数展开,去除与方位无关的背景项,提取反映裂缝各向异性的二阶傅里叶系数预测裂缝发育情况。所提方法与基于方位地震振幅数据的方法相比,能够直接反映地层内部裂缝发育情况。为了准确预测裂缝面法向,提出了互相关裂缝法向预测方法,解决了当实际裂缝面法向方位角大于90°时,无法准确预测的难题。模型数据预测结果与真实模型基本一致,实际数据预测结果与成像测井结果一致,具有较高精度。
