融合轨枕检测和卡尔曼滤波的中低速磁浮列车测速定位优化算法研究*

潘洪亮 邱 宇 唐少强

(1.同济大学道路与交通工程教育部重点实验室， 201804， 上海； 2.同济大学磁浮交通工程技术研究中心， 201804， 上海∥第一作者， 副研究员)

计数轨枕测速定位是一种在中低速磁浮领域使用较多的列车测速定位方法。该方法具有设备简单、造价低、易于安装等优点，使其成为解决中低速磁浮列车测速定位较好的解决方案。但是，该方法存在低速时测速不准、高速时脉冲可能漏检等问题[1]，其可靠性和检测精度难以保证。本文在文献[2]的基础上，克服了列车振动和计时误差等因素，对该方法作进一步的改进，以得到更为可靠、准确的速度和位置信息。

1 检测方法及原理

1.1 基于钢轨轨枕的计数检测方法

中低速磁浮线路在轨道结构中布置钢轨轨枕，电感式涡流传感器经过钢轨轨枕时会产生脉冲信号，通过累计磁浮列车经过的钢轨轨枕数目，结合轨枕间距，就可以实现对列车运行距离、运行速度等运动学参数的计算。文献[2]中，在线路上相邻传感器间距D固定的情况下，可利用列车通过相邻传感器的时间差ΔT来计算列车的运行速度V：

(1)

基于钢轨轨枕的测速定位方法原理如图1所示。此方法只需要在工程应用中控制D的精度，即可实现对列车的测速定位。由于中低速磁浮线路轨道的选线型式多样、轨道转弯时存在内径和外径的差别、线路上存在车站、桥梁、道岔等特殊区段，采用该方法进行检测时存在一定的难度，因此，在实际的工程应用中不会单独采用钢轨轨枕计数方法来实现列车的测速定位。

a) 整体布置

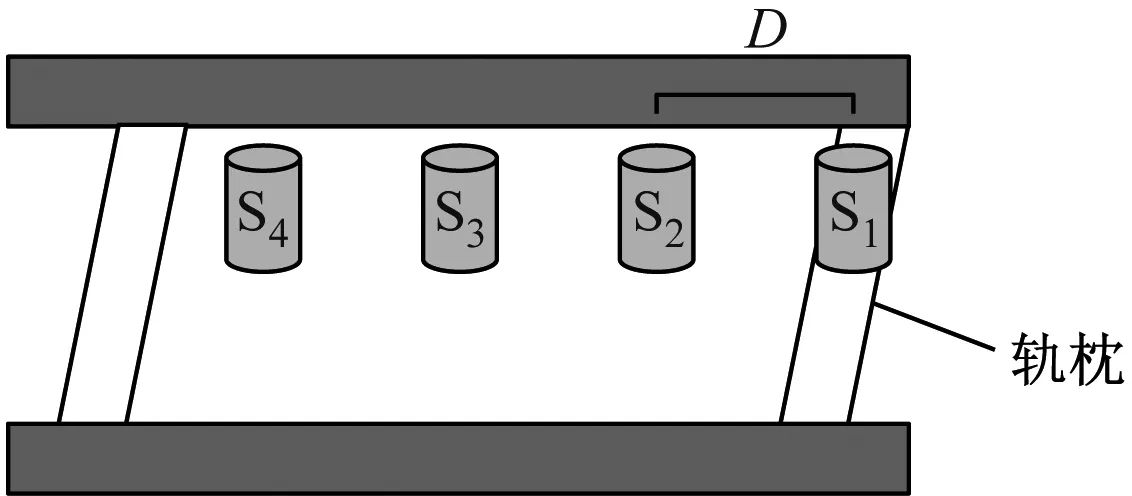
b) 涡流传感器与轨枕位置关系注：S1、S2、S3、S4为传感器。图1 基于钢轨轨枕的测速定位方法原理

1.2 卡尔曼滤波原理

卡尔曼滤波是当前广泛使用的一种滤波方法，其基本思想为利用上一时刻预测的此时刻状态及此时刻的观测状态来找到最接近真实状态的解。假设线性离散系统的数学模型为[3]：

X(k)=F(k,k-1)X(k-1)+Γ(k,k-1)A(k)

(2)

C(k)=H(k)X(k)+B(k)

(3)

式中：

X(k)——k时刻的系统状态向量；

X(k-1)——k-1时刻的系统状态向量；

F(k,k-1)——k-1时刻到k时刻的系统状态转移矩阵；

Γ(k,k-1)——k-1时刻到k时刻的系统噪声矩阵；

A(k)——k时刻的系统噪声向量；

C(k)——k时刻的系统观测向量；

H(k)——k时刻的系统观测矩阵；

B(k)——k时刻的量测噪声矩阵；

k——列车运行的某一时刻。

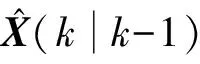
(4)

P(k|k-1)=F(k,k-1)P(k-1)FT(k,k-1)+

Γ(k,k-1)A(k-1)ΓT(k,k-1)

(5)

式中：

P(k-1)——k-1时刻的系统估计协方差；

P(k|k-1)——由k-1时刻预测的k时刻系统估计协方差；

A(k-1)——k-1时刻的系统噪声向量。

求解卡尔曼滤波系数K，其计算式为：

(6)

式中：

K(k)——k时刻卡尔曼滤波的增益；

R(k)——k时刻量测的噪声协方差矩阵。

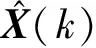
(7)

P(k)=[I-K(k)H(k)]P(k|>k-1)

(8)

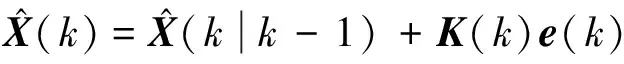
(9)

式中：

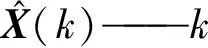
e(k)——k时刻残差；

I——单位矩阵。

2 融合轨枕检测和卡尔曼滤波的优化算法

2.1 对传统轨枕检测方法的优化

2.1.1 对传统轨枕检测方法的优化计算

在理想情况下，每个涡流传感器均能在某一时刻到达金属轨枕上方。基于此原则，记录每个脉冲的上升沿时间Tij，从而得到时间矩阵

(10)

其中：i表示第i个传感器所记录的时间序列，i≤m；j代表第j个金属轨枕，j≤n。m个传感器依次通过同一个金属轨枕后再依次通过下一个金属轨枕，算得相邻传感器通过同一轨枕的速度Vij=D/(Tij-T(i-1)j)。但是在实际的运行中，由于存在列车抖动、传感器误差、记时器误差等因素，将此时传感器到达金属轨枕后记录的上升沿时间记为tij,则tij与实际时间Tij之间会有一定偏差，即tij=Tij+lij,lij为所记录时间的随机噪声。设Td为实际测量的时间矩阵，vij为实际情况下相邻传感器通过同一轨枕后所计算得到的速度,则有：

(11)

(12)

假设中低速磁浮列车以10 m/s匀速运行，若D=0.3 m，则通过相邻传感器的时间为0.03 s，中间间隔1个传感器时的通过时间为0.06 s，中间间隔2个传感器时的通过时间为0.09 s。即使列车以0.09 s的时间间隔进行采样，仍然能及时获取列车的速度位移信息。而计数轨枕方法的实质是计算2个传感器均以某个平均速度通过一定距离时脉冲上升沿的时间差，以获得一定位移下的间隔时间，因此，当列车的速度较为稳定时，位移越大，在相同时间误差情况下对速度的大小影响越小，速度与真实值越接近。在速度较大时，相邻传感器经过同一金属轨枕时的时间间隔亦较小。

重复上面的计算步骤，计算中间间隔2个传感器时的通过时间及其矩阵群，对得到的速度数据进行加权平均，则可以得到中间间隔了2个传感器时的列车运行平均速度。以此类推。

2.1.2 不同运行条件下列车运行平均速度的计算

在进行优化计算时，一方面应考虑到时间误差对速度的影响，另一方面还应考虑速度的准确性。上文的优化方法可根据不同速度采用不同的算法来处理数据。可按照以下条件分类计算速度：

1) 条件一，当列车低速行驶或列车的加/减速度较大时，采用一般算法，计算每个相邻传感器通过金属轨枕时所记录时间的速度；

2) 条件二，当列车速度较大且加/减速度较小时，视列车在通过1个轨枕时速度为匀速，按中间间隔了1个传感器的情况计算其平均速度。

2.2 冗余轨枕检测优化算法

为了得到更为精确、可靠的列车速度及位置信息，本文在传感器安装上作了进一步的优化。在列车的车头及车尾各安装4个传感器，将车头的4个传感器作为第1套测速定位设备,将车尾的4个传感器作为第2套测速定位设备，则列车有2套测速定位设备，构成测速定位的冗余。将车头编号为1，车尾编号为2，则列车在k时刻经过轨枕j时的平均运行速度为：

v0,k=w1,kv1,k+w2,kv2,k

(13)

式中：

v0,k——在k时刻采用2套测速定位设备采集得到的速度的加权平均值；

v1,k——在k时刻车头定位设备的测速数据；

v2,k——在k时刻车尾测速定位设备的测速数据；

w1,k——在k时刻车头测速数据的权值；

w2,k——在k时刻车尾测速数据的权值。

2.3 融合卡尔曼滤波的优化算法

列车大部分时间运行于匀加速或匀速状态，因此可建立模型如下：

(14)

(15)

式中：

sk-1、sk——分别为k-1时刻、k时刻列车的预测位移值；

vk-1、vk——分别为k-1时刻、k时刻列车的预测速度值；

Sk——k时刻列车的观测位移值；

T0——脉冲上升沿间隔时间;

a(k)——k时刻机动加速度和随机加速度之和；

B(k)——k时刻观测噪声矩阵。

y1,k=(v1,k-vk)2

(16)

y2,k=(v2,k-vk)2

(17)

(18)

(19)

式中：

y1,k——k时刻车头传感器观测值与预测值的差值；

y2,k——k时刻车尾传感器观测值与预测值的差值;

w1,k+1——k+1时刻车头测速数据的权值;

w2,k+2——k+1时刻车尾测速数据的权值。

将w1,k+1、w2,k+1代入式(13),即可得到k+1时刻的速度观测值的输入。在计算y1,k和y2,k时，应根据经验设定一个阈值，当某一测速定位设备在一定的时间段内所计算得到的差值有95%落在此阈值区间之外时，则可认为此设备发生了软故障，将此套设备后面数据权值定为0。

整个测速定位算法的流程如图2所示。

图2 融合轨枕检测和卡尔曼滤波的列车测速定位算法流程图

3 算例验证

3.1 仿真基础数据

本次仿真基于上海临港中低速磁浮试验线，利用Matlab软件进行仿真。假定该线的中低速磁浮列车以1.0 m/s2的加速度开始运行，10 s后列车的速度为10.0 m/s，此时列车匀速向前行驶，行驶至958.33 m后改为以1.2 m/s2的减速度继续行驶，最终行驶到1 km处速度为0 m/s。

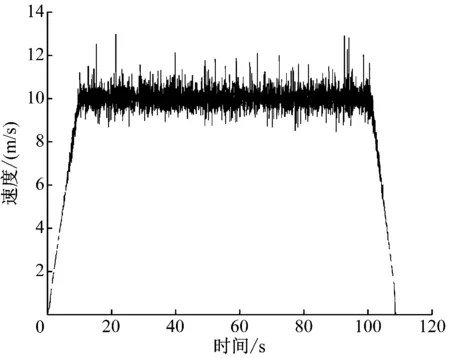
图3 条件一下的监测数据仿真得到的列车速度-时间曲线

3.2 仿真结果分析

3.2.1 传统轨枕检测测速定位算法的仿真结果

由图3可知，在列车以10 m/s匀速运行阶段，其按条件一的计算方法，速度曲线波动较大。若用上述满足条件二时的计算方法进行计算，可得到条件二下匀速运行阶段的列车速度-时间曲线如图4所示。

与图3相比，图4的曲线波动明显减少。为证明此结论，本文对不同监测方法下的速度方差进行了计算：①条件一下计算得到的列车平均运行速度的方差为0.056 614 576；②条件二下计算得到的列车运行平均速度的方差为0.036 520 903。由此可得出如下结论：在传感器间隔为0.3 m的情况下，由于涡流传感器采样存在误差，其速度曲线波动大于间隔采样下的波动，且间隔的传感器越多，其速度方差越小。因此，在考虑了时间误差对速度的影响及速度的准确性后，此算法是对原始算法的优化。

图4 条件二下的监测数据仿真得到的列车速度-时间曲线

3.2.2 冗余测速定位算法的仿真结果

上文对监测数据在生成初始速度后已进行了优化。本文对该优化数据利用卡尔曼进行基础滤波，结果如图5所示。图例中的“真实”表示列车在线路上运行时实际的列车速度-位移曲线；“观测”表示条件二下仿真计算得到的观测列车速度-位移曲线；“滤波(1组)”表示采用卡尔曼滤波对一套测速设备监测得到的观测数据进行优化得到的列车位移-速度曲线。

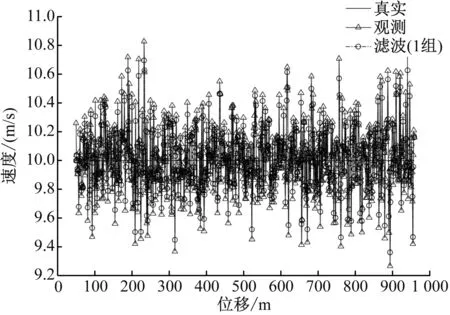
图5 对一套测速装置的监测数据进行卡尔曼基础滤波后的列车位移-速度曲线

从图5中可以看出，监测数据经过基础滤波处理后有一定的滤波效果，其波动相较原始滤波有了一定程度的改善。为取得更好的监测效果，在已有第一套速度传感器的基础上，再引入第二套速度传感器。按照上文融合卡尔曼滤波的优化算法将数据进行再次处理，结果如图6所示。图例中的“真实”、“观测”的含义同图5；“滤波(两组)”表示采用卡尔曼滤波对两套测速设备得到观测数据进行优化得到的列车位移-速度曲线。

图6 对两套测速装置的监测数据进行卡尔曼优化后的列车位移-速度曲线

从图5～6可以看出,与使用一套测速设备得到的监测数据相比,使用两套测速设备得到的数据进行融合卡尔曼滤波优化后的数据有较大的提升。为证明与采样一套测速设备的定位数据相比，采用两套测速设备的定位效果更优，本文选取匀速运行采样数据，计算采样数据与原始数据差值的绝对值，分别生成位移误差均方根的上下包络线，如图7所示。

从图7可以看出，采用一套测速设备进行监测得到的速度、位移数据经卡尔曼滤波后，其速度、位移的精度要优于原始的速度、位移数据；采用两套测速设备进行监测得到的速度、位移数据经优化后最优。这证明本文所研究的算法能有效优化速度、位移数据，可提高列车测速定位的精度，改善其测速定位效果。

4 结语

本文针对既有基于轨枕检测测速定位方法的不足，提出采用两套测速定位设备对列车的速度、位移数据进行采集，利用卡尔曼滤波自适应权值的方法，对列车的定位算法进行优化，并通过计算机仿真该优化算法的测速定位效果。仿真结果证明：

a) 上包络线

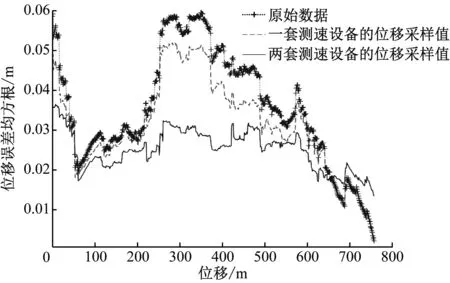
b) 下包络线图7 列车位移-位移误差均方根曲线包络线对比

本文所提出的优化算法能有效改善列车振动、时钟误差等因素导致的速度计算误差，显著提高基于轨枕检测的测速定位方法的可靠性及精确性。在此优化算法的基础上，若添加其他辅助的测速定位设备(如应答器、测速雷达、加速度计等)[4]，可为中低速磁浮列车的测速定位提供更为可靠且安全的测速定位功能。