昆明市主要城市公园绿地土壤入渗性能及差异性分析

王刘雅 马建刚

（西南林业大学生态与环境学院，云南 昆明 650233）

海绵城市建设是我国城市水文环境改善的重要内容，其不仅要有好的工程设施，更要充分发挥现有城市海绵体“城市绿地”的作用[1]。城市绿地作为城市生态系统中仅存的保留有水气循环功能的组成部分，对改善城市生态环境，减少地表径流流量、污染，增强土壤渗透性，减轻土壤的侵蚀，回补地下水具有重要作用[2-3]。

土壤入渗性能是土壤基础属性之一，在降水、地表水、土壤水以及地下水的转化过程中担当重要角色。开展城市绿地土壤入渗性能研究，是海绵城市建设的一个重要环节，对增加城市雨水地表入渗，减轻城市内涝有着重要意义[4]。由于城市绿地土壤受到众多人为因素的影响，物理特性在不同的区域、不同植被以及不同管理应用条件下表现出较大的变异性[5-6]，尤其是城市土壤压实现象比较突出，引起的土壤剖面上的容重、孔隙等物理性状变差[7-10]，进一步引起水分入渗及水分再分布方面的恶化，限制了城市绿地土壤调洪蓄水、供给植物水分的作用[10-12]。

随着城市绿地面积逐年增长，越来越多的学者开始关注绿地土壤的入渗性能。以往的城市绿地土壤水分入渗研究中，以剖面整体入渗为主要研究内容[13-14]，对掌握城市绿地土壤的宏观上的海绵体作用具有积极意义。已有的少量研究表明，城市绿地不同深度土壤的渗透性差异很大，随着土壤深度的增加，水分渗透能力迅速下降[15]。但土壤剖面不同层次水分导渗是否有差异，是否有水分调蓄的土壤障碍层、突变层，目前尚没有充分开展研究。鉴于此，本研究针对昆明市主要公园绿地土壤不同深度上的水分渗透过程开展了研究分析，以期揭示绿地土壤水分入渗随着深度变化的规律，探究公园绿地是否存在中间障碍层，为公园绿地管理和城市雨洪计算提供参考。

1 研究区概况

昆明市位于中国西南云贵高原中部（102°10′～103°40′E，24°23′～26°22′N），昆明市平均海拔约1 894 m。属北亚热带低纬高原山地季风气候，市辖区多年均降雨量1 035 mm，全年降水量在时间分布上，明显地分为干、湿两季，5—10月为雨季，降水量占全年的85%左右，11月至次年4月为干季，降水量仅占全年的15%左右。截至2017年底，全市主城建成区绿地面积达16 081.57 hm2，公园绿地面积3 885.57 hm2，主城建成区人均公园绿地面积接近11 m2，部分新建公园及其绿地正在规划和建设中。植被以亚热带常绿阔叶林为主，植物种类丰茂。土壤包含十多个土类，以酸性红壤为主要土壤类型。

2 研究方法

2.1 样地选择

选择昆明市的4个市属公园：昙华寺公园（昆明市东部、面积约8 hm2，绿化率约28.7%）、大观公园（昆明市西南，面积约28.6 hm2，绿化率约32%）、黑龙潭公园（昆明市北郊，游览区面积约50 hm2，绿化率约70%）和郊野公园（昆明市西郊，面积约162 hm2，绿化率约85%）。大观公园紧邻滇池，昙华寺公园位于金汁河畔，属于滨水型公园，地形都比较平坦；而黑龙潭公园和郊野公园是面积较大、距市区较远且山体坡度大的山地型公园。4个公园建成时间均超过20年，历史悠久，海拔在1 886～1 924 m。公园内植物种类丰富，土壤类型主要为红壤。按照“植物种数量及分布较多、立地条件相似、同一生活型物种生态学特征相似”的原则选择样地，在每一公园内选择乔灌草（G1）、灌草（G2）、乔草（G3）3种植物搭配类型绿地，其中主要乔木为滇润楠（Machilus yunnanensis）、香樟（Cinnamomum camphora），主要灌木为雀舌黄杨（Buxus bodinieri）、红花檵木（Loropetalum chinensevar.rubrumm），草本主要为马尼拉草（Zoysia matrella），局部混有早熟禾（Poa annua）。试验点土壤以轻粘土为主，局部为中粘土，植被盖度均超过80%，选择样点坡度介于0°～3°，共12个试验样地。

2.2 入渗试验设计

入渗试验采用Guelph入渗仪（型号：2800k1；Soilmoisture Equipment Corp，美国）进行，Guelph入渗仪基于马里奥特瓶原理及三维流原理，由供水部件和入渗部件组成（图1），水从入渗仪缓慢流入土壤中，土壤在某一时刻形成饱和状态，从入渗仪中流出的水也将达到一个恒定值（可测量出）。根据测量数据，以及钻孔直径和钻孔内水位，便可计算出任一时刻的入渗速率和饱和状态下土壤的导水率。

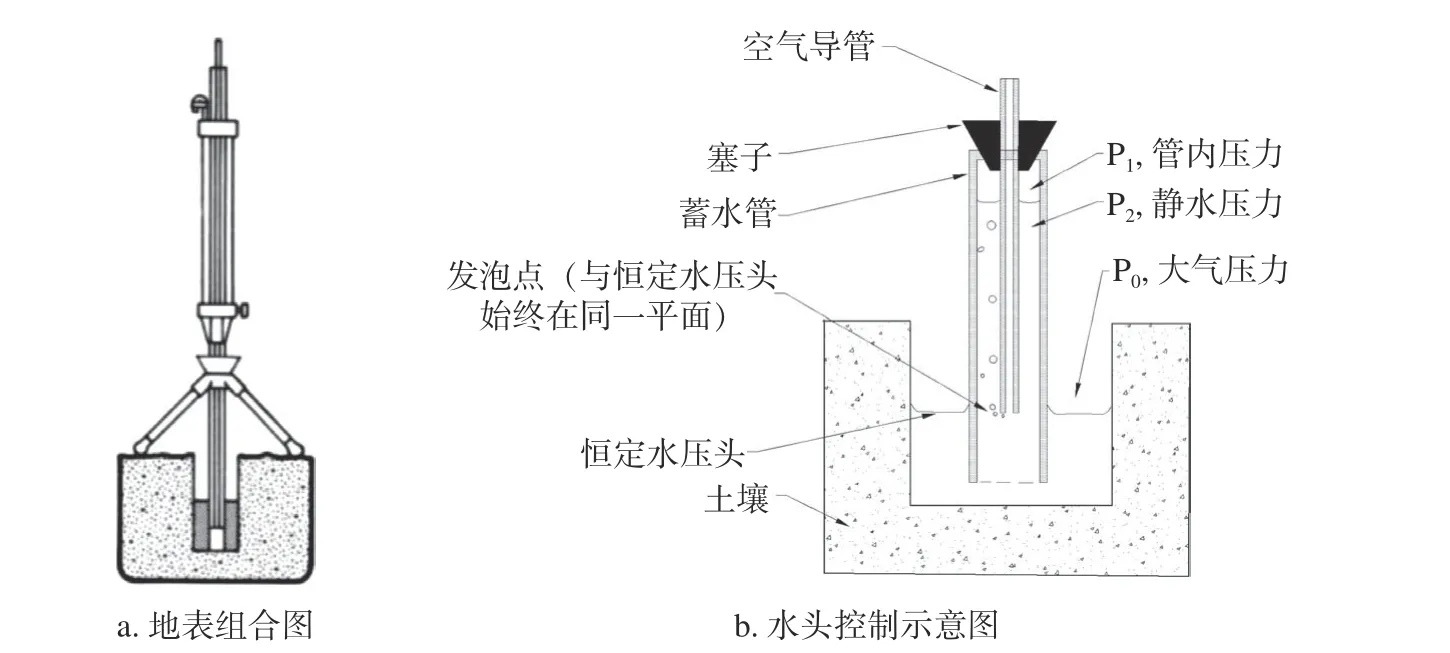
图 1 Guelph入渗仪示意图Fig. 1 Schematic diagram of Guelph infiltration meter

此次试验于2017年10月选择连续48 h内无降水、无浇水的情况下进行现场测试。试验过程如下：1）选择合适的位置打孔，入渗孔深度分别为10、20、40、60 cm，每个土孔间距不小于2.0 m；2）安装Guelph入渗仪，保证各接触口连接到位，同时使度量管的刻度在水位指示器底部显示为5 cm；3）将水注入蓄水管中，并堵住排气口；4）将管子放入土壤孔内，设置5 cm水头，每分钟记录1次蓄水管中水位变化的读数，直到取得入渗量读数稳定的5个值时结束。每个土孔测定1次入渗过程。

2.3 土壤物理指标测定

在12个入渗试验样地上，采用环刀法分别测定0～10、10～20、20～40、40～60 cm的土壤容重、总孔隙度和含水量（按照土壤剖面层次，由上至下用环刀在每层的中部采样[16]）。

2.4 水分入渗参数计算

按照单水头法[17]计算每个测定点的入渗速率，计算公式如下：

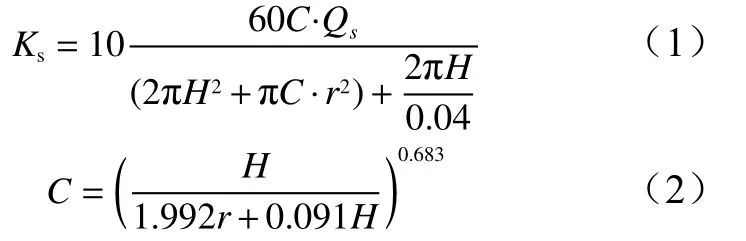
式中：10为单位换算系数；Ks为 入渗速率（mm/min）；C为形状系数，无量纲；H为压力水头（5.0cm）；Qs为水流通量（cm3/s），通过设备直接计算；r为洞口半径（3.0 cm）。

初始入渗速率（f0）取前2 min的平均入渗速率（mm/min）；稳定入渗速率（fc）为采用试验末入渗速率标准偏差小于0.5%的3～5个值的平均值（mm/min）；稳渗时间（T）为达到第1个稳渗值时的时长（min）；平均入渗速率（fa）为达稳渗后第1个值截至时所有入渗速率的平均值（mm/min）；1 h累计入渗量（ft）为入渗过程1 h时长内的累计入渗量（mm）。

2.5 土壤入渗模型选择

为了选出适合试验区进行土壤水分入渗过程预测的最佳模型，选择Kostiskov模型、Horton模型、Philip模型和通用经验公式，对入渗试验获得的时间与累积入渗量数据按模型形式进行拟合，Kostiskov模型、Horton模型、Philip模型、通用经验公式结构分别见（3）～（6）。

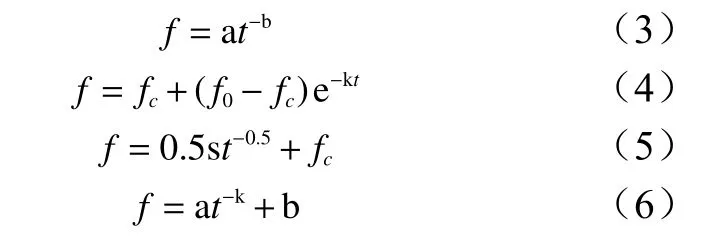
式中：f为入渗速率，t为入渗时间；a为第1个单位时间末的入渗速率；b为经验指数，根据土壤性质和初始含水率而定，变化于0.3～0.8之间；k为反映土壤特性的常数；e为自然常数。s为土壤特性常数，其大小与土壤初始含水率有关，可通过初期入渗总量决定。

3 结果与分析

3.1 土壤容重与孔隙

土壤容重与孔隙受人为踩踏影响最为明显，也是影响水分入渗的主导因素[10,14]。本研究区随着土层的深入，公园绿地土壤容重呈增加趋势，孔隙度为减小趋势（见表1）。土壤总孔隙中有6个最大值（占比50%）出现在10～20 cm的亚表层，最小值集中在土壤底层；容重最大值分别在10～20、20～40、40～60 cm各出现了4次，最小值全部是表层，说明由于根系的存在减小了部分绿地表层土壤容重，但是孔隙状况并不是最优。各类绿地中乔草绿地各层土壤容重均是最大的，均值达到为1.44 g/cm3，只有3个0～10 cm土壤容重值小于《绿化种植土壤》（CJ/T 340—2016）[18]标准的规定（<1.35 g/cm3）。其余绿地土壤容重小于1.35 g/cm3占93.7%，灌草绿地容重平均为1.23 g/cm3，乔灌草为1.22 g/cm3。乔草绿地的孔隙状况也是最差的（乔灌草（49.97%）>灌草绿地（47.67%）>乔草绿地（47.00%）），说明乔草绿地可能是3类公园绿地中受人为干扰最严重的区域。方差分析表明，不同土层间的总孔隙度、容重、土壤含水量差异达均到显著差异水平（P<0.05）。土壤水分含量表层和底部低，最大值集中出现在20～40 cm。

表 1 土壤容重、孔隙与土壤含水量Table 1 Soil bulk density, pores and soil moisture

3.2 水分入渗参数特征

入渗试验结果见表2。由表2可知，不同入渗孔深度下，各参数最大值出现在10 cm和20 cm的平均占比为83.3%，最小值出现在40 cm和60 cm层次的占比为81.7%。12组稳渗数据中，最大值出现在10、20 cm入渗孔上的个数分别是9个和3个，最小值在最后2层分别出现2个和8个；在前后两两对比中的36组稳渗数据中，有8个稳渗值比上层增加，其余均减小，减小组环比递减率为21.8%，增加组环比递增速率达到70.7%，主要是由于郊野公园乔草地20 cm入渗孔稳渗速率是2.40 mm/min，是10 cm孔入渗速率的5.34倍，导致整体增加环比值较大。

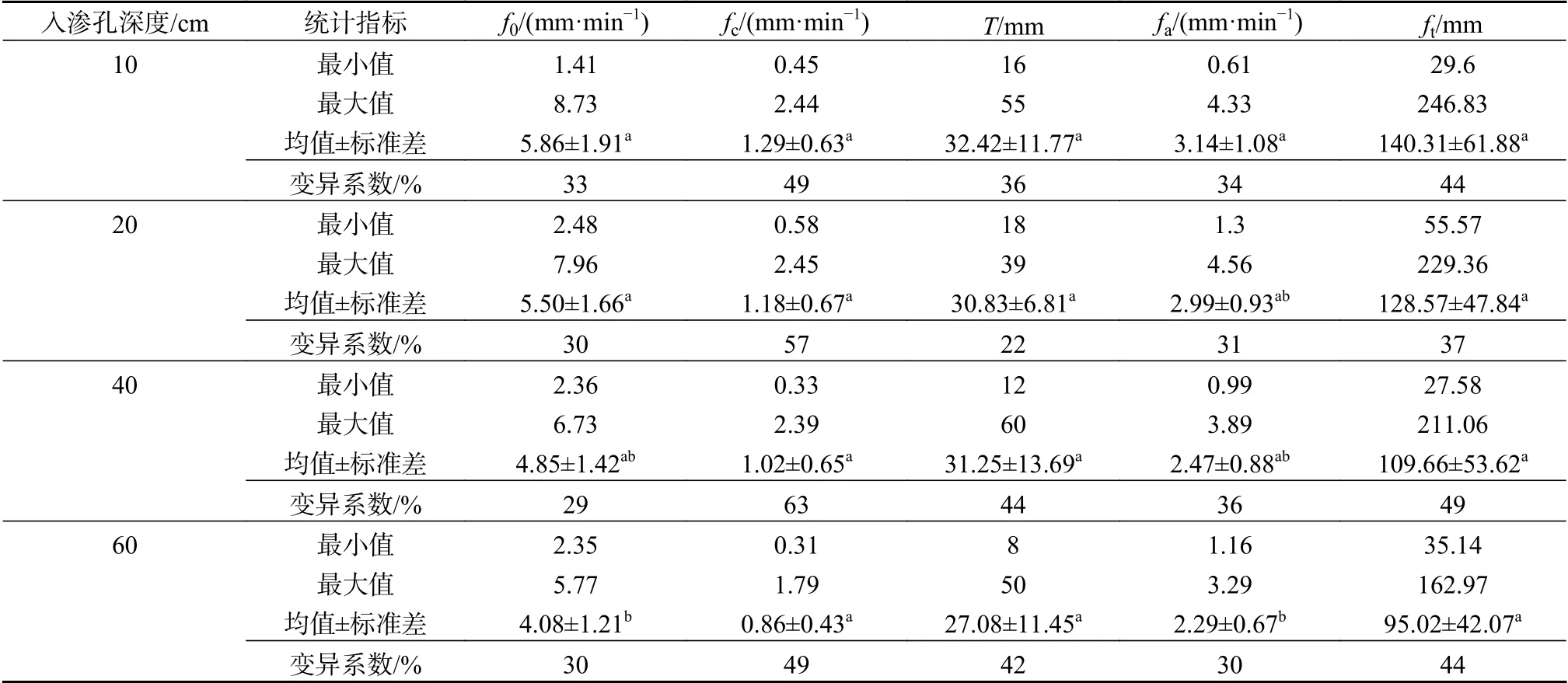
表 2 入渗参数统计表Table 2 Statistics of infiltration parameters

不同公园、不同植被间同一层次土壤稳渗速率变异系数大部分在50%左右，属于中等变异；同一植被类型或总体均值不同层次间的变异系数为17%～25%，属于中等变异。不同深度土壤入渗参数特征见图2。由图2可知，土壤入渗性能随着入渗孔的深度增加而减小的趋势，初渗速率和稳渗速率随着入渗孔的深度增加而减小的量也明显增大，然而通过方差分析表明，只有初渗速率、平均入渗速率差异达到显著水平（P<0.05），稳定入渗速率等其余参数差异均不显著。

不同绿地上，乔灌草、灌草绿地最小值均出现于后2层，乔草地前2层和后2层各有50%最小值；最大值分布在不同绿地上没有明显规律，主要集中在5、20 cm的入渗孔上，占比达82%。稳定入渗速率总体均值从大到小依次为乔灌草（1.31 mm/min）> 灌草（1.03 mm/min）> 乔 草（0.96 mm/min）。乔草的初渗、累计入渗量均值也是最小，主要是由于乔草是各公园对人员活动开放的主要绿地类型，踩踏最为严重，乔草地土壤总孔隙度均值最小（47%），容重均值最大（1.45 g/cm3）。但不同植被、不同深度下进行方差分析，稳渗值差异不显著。

昙华寺公园各类绿地以及总体均值达到稳渗时间都是最少，初渗及稳渗速率、累计入渗量也都是最小，主要是由于昙华寺公园面积最小，是昆明市东部区域居民最常去的公园，绿地开放程度高，游客频次较大，引起较显著的地面踩踏扰动，该处土壤容重均值最大（1.33 g/cm3）、总孔隙度均值最小（45.36%）。不同公园间稳渗值差异达到显著水平（P<0.05）。

3.3 入渗过程分析

随着入渗时间的增加，入渗速率逐渐降低直至趋于稳定，到达稳渗的时间分布在8～60 min，主要集中在20～40 min。土壤稳渗时间特征见图3。由图3可知，4个深度入渗孔平均达到稳渗的时间依次为：34.42、30.83、31.25、27.08 min，各层次间到达稳渗的时间差异不显著。3种植被类型下平均达到稳渗的时间分别为：乔灌草31.63 min、灌草29.06 min、乔草30.50 min，不同植被间达到稳渗的时间差异不显著。昙华寺、大观公园、黑龙潭、郊野公园平均达到稳渗的时间分别为21.50、41.08、27.08、31.92 min，不同公园间达到稳渗的时间差异显著（P<0.05）。

图 3 土壤稳渗时间特征Fig. 3 Characteristics of soil stable infiltration time

3.4 土壤入渗模型分析

利用Kostiskov模型、Horton模型、Philip模型和通用经验公式分别对样本区内各点土壤入渗速率进行拟合，各模型决定系数（R2）见表3。

决定系数R2越大，模型拟合效果越好。由表3可知，各模型拟合效果在40 cm的土层中均较好，其中Philip模型拟合效果最差；各模型在乔灌草绿地土壤中拟合效果较好，通用公式在3种植被类型下拟合度均是最高；各模型拟合效果在黑龙潭公园中较好，Horton模型和通用公式拟合最优。总的来说，通用公式的拟合效果最好，其次是Horton模型，R2均在0.87以上。通过回归分析F检验法对模型进行显著性检验，结果表明：Philip模型没有达到显著水平，Kostiskow模型和Horton模型达到显著水平，通用公式达到了极显著水平。

表 3 不同模型下的R2值统计Table 3 R2 value statistics under different models

4 结论与讨论

通过对昆明市主要城市公园绿地土壤水分入渗性能及其差异性的研究，主要得出以下结论：1）土壤入渗性能在不同植被类型、不同土壤深度上有着较为明显的差异性，为弱至中等程度变异，其中乔灌草绿地土壤最优，乔草土壤最差，入渗性能随着深度的增加减弱，存在约1/3的剖面中间障碍层的表达，但稳渗值差异并不显著，认为无明显的土壤中间入渗障碍层；2）稳渗值在不同公园间变异为中等变异且差异性显著，稳定入渗速率依次为：昙华寺公园0.68 mm/min；黑龙潭公园0.89 mm/min；大观公园1.01 mm/min；郊野公园1.78 mm/min；3）通用公式是对昆明城市公园绿地入渗过程模拟的最佳公式。

土壤容重与孔隙是影响土壤入渗的关键因子，容重小、孔隙多入渗速率一般较大，反之则小[11,19]。本研究中不同绿地上的入渗性能以乔灌草最优，其次为灌草绿地、乔草绿地，这可能是由于公园草地和具有良好遮荫的林草地也是入园游客最喜进入的绿地斑块[20]，容易被踩踏，导致土壤物理性状变差；乔草绿地土壤内细根系不如乔灌草、灌草绿地分布多，也导致入渗性能相对较差，这与伍海兵[21]在上海辰山植物园中的研究结果一致，均表现出草地和纯乔木林地是土壤物理状况及饱和导水率最差的。土壤表层由于细根的存在以及有机质丰富等原因，容重最小；土壤孔隙度在亚表层均出现过最大值，说明亚表层受到地面踩踏后影响最为严重。熊圣洲[15]、黄晖等[22]对深圳市各类绿地土壤入渗的研究都表明各项渗透参数均显示出随土壤深度增加而逐渐下降的变化趋势，与本研究不同的是熊圣洲的研究测得的各入渗参数值明显大于本研究均值1.09 mm/min，而黄晖的研究结果（稳渗均值为0.906 mm/min）小于本研究的均值，并且本次研究与2014年在同一样地使用双环法测定的稳渗值（0.83 mm/min）[13]相比也大，说明入渗参数具有明显的时空分异性。各项入渗指标在不同植被、不同土层间差异不显著，但是在不同公园间差异显著。4个公园中的昙华寺公园面积及绿化率最小，单位面积游客承载量最大，这说明人为活动也是影响城市公园土壤水分入渗的主要因素。

各种组合下土壤稳渗速率与容重均呈负相关性，与孔隙呈正相关性；公园绿地土壤稳渗系数在不同植被和不同公园间大于剖面上的变异系数，说明研究区公园人类活动干扰、植被结构等对土壤入渗性能的影响更为突出。在本研究中的12个样地的不同层次稳渗速率中，有4个样地最小值并不是在最下层，分别出现在灌草10～20 cm 1个、20～40 cm 2个，乔草0～10 cm 1个，相应的4个位置的容重偏大，总孔隙度偏小，说明公园绿地入渗性能在剖面中间具有一定的障碍层表达，但稳渗值在不同层次间差异并不显著，中间低值比例也较低（33.3%），可以认为入渗中间障碍层并不显著。由于本研究只针对昆明市主要城市公园绿地进行了研究分析，对于城市绿地的总体判断还有待深入研究。

各样地达到稳渗的时间在不同植被间和不同土层间虽有一定的差异，但差异并不显著，这与土壤孔隙、容重的差异并不一致。应该是由于土壤入渗不仅受到土壤孔隙、容重的影响，也受到土壤结构及有机质等的影响[23]。而在不同公园间稳渗时间差异显著，主要是由于昙华寺公园稳渗值较小，引起了差异的显著性。

本研究及前人的研究[10-11,13,15,24]表明，通用公式、Horton模型、Kostiskow模型都能较好地适用于城市绿地土壤入渗过程的模拟。Philip模型适用性较差，是由于Guelph入渗仪水分入渗过程，是水分在土壤里面呈水滴状的扩散过程，并不是单纯的一维入渗，而Philip入渗模型更适用于一维入渗模拟[25]。昆明市公园绿地最适模型是通用公式，这与许丽等[26]在阿拉尔市的研究结果相同。因此，研究城市绿地土壤入渗性能时，建议采用通用公式。