改进蚁群算法的移动机器人路径规划

唐旭晖，辛绍杰

上海电机学院 机械学院，上海 201306

移动机器人的路径规划是指，在机器人位姿与环境信息都已知的情形下，寻找出一条自起点至目标点的无碰撞最优路径。路径规划问题的核心便是路径规划算法，目前可分为传统规划算法和仿生群智能优化算法。其中，传统路径规划方法有Dijkstra算法[1]、A*算法[2]、RRT算法[3]等，随着群智能优化算法的发展，粒子群算法[4]、蚁群算法[5]、灰狼算法[6]等也逐渐在路径规划的应用中崭露头角。本文选择的蚁群算法（ant colony optimization）是意大利学者Dorigo等人提出的一种基于状态转移概率和信息素更新机制的模拟蚁群觅食过程的智能算法，随迭代次数增加，蚁群始终能在全局环境下搜索到一条最优路径，但是该算法的收敛速度慢且易陷入局部最优。徐菱等人[7]提出一种基于16方向24邻域的搜索方式，结合向量夹角改进启发信息，增加蚁群搜索范围，提高全局搜索能力。封声飞等人[8]提出一种自适应蚁群算法，根据环境信息自适应调节初始信息素，并采取信息素排序择优更新机制，提升了算法收敛速度。张强等人[9]以改进人工势场算法为蚁群规划出起始路径，避免早期的盲目搜索，并构建负反馈机制，使信息素更新根据收敛次数自调节，增强收敛速度与全局寻优的协调性。针对传统蚁群算法的收敛速度慢与易陷入局部最优问题，本文提出一种改进的蚁群算法，其中包括：根据环境信息构建目标点导向区，增强目标点导向区的初始信息素浓度，提高蚁群初期搜索方向的导向性；对地图分块处理并检测路径折点信息，通过叉积运算进行局部优化，改善路径的曲折状况；改进基于精英策略蚁群算法的精英信息素增强因子，并添加随环境变化可自适应调节的衰减因子，同时引入随机状态转移参数，提高蚁群搜索的随机性，避免陷入局部最优，增强算法局部优化和全局寻优能力的平衡性。

1 路径规划环境建模

本文基于栅格地图进行改进算法的路径规划分析，栅格地图建模如下：构造环境矩阵G，定义矩阵G中元素0和1分别记为可行节点和障碍物节点。根据对应关系将矩阵G转化为邻接矩阵D，邻接矩阵D中为栅格图各节点间的通行代价，定义各节点间仅可相邻或对角通行，相邻和对角节点通行代价分别记为1和1.4，不可通行代价记为0，其转换形式如图1所示。

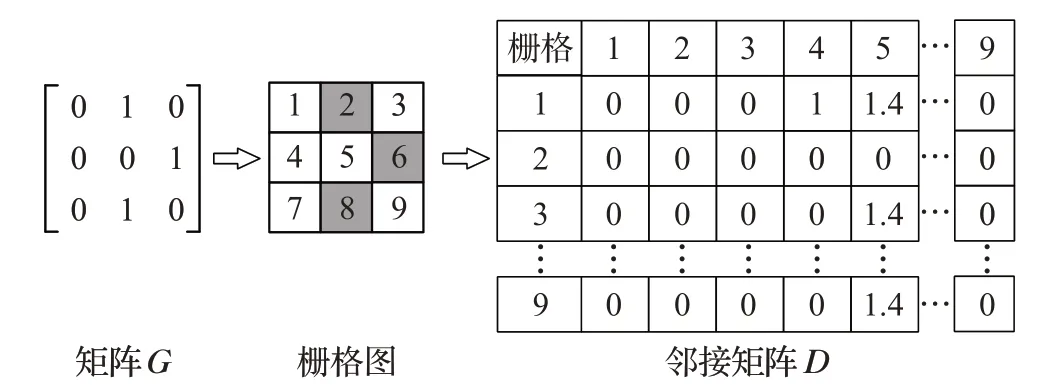
图1 节点图转换示例Fig.1 Example of node diagram conversion

2 蚁群算法

传统蚁群算法采取轮盘赌法的机制进行路径节点选择，其状态转移概率如式（1）、（2）所示：

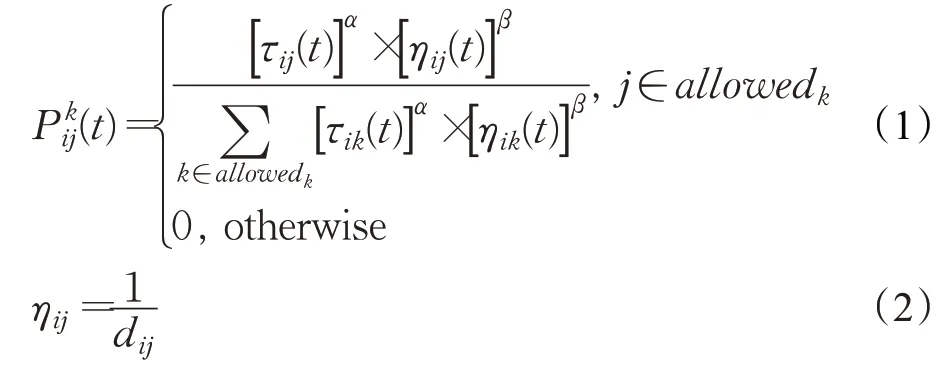
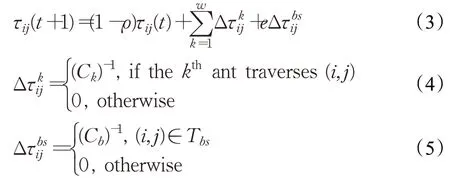
式（3）为精英蚁群算法[10]信息素更新模型，其中，ρ为挥发系数，为第k只蚂蚁经过(i,j)路段的信息素增量，w为蚂蚁总数，e为最优路径信息素增强权重系数，为最优路径信息素增量。Ck是第k只蚂蚁所走路径总长，Cb为最优路径Tbs的总路长。

3 改进蚁群算法

3.1 构建目标点导向区

蚁群算法最初用于解决TSP问题，现将其应用于移动机器人的路径规划问题后，路径节点的选取过程中，部分小区域内的节点对产生最优路径的影响效益小，如示意图2所示。

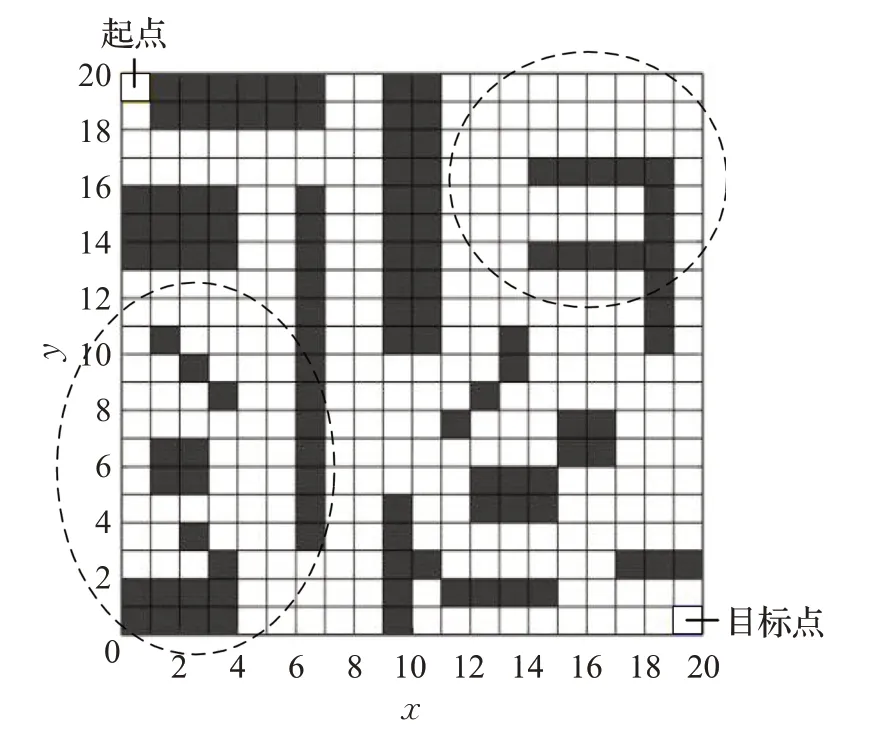
图2 20×20环境示例Fig.2 Example of 20×20 environment

如图2所示，在该20×20环境下若定义左上角为起点，右下角为移动机器人需到达的终点，则可发现在最优路径搜寻过程中，虚线椭圆范围内的节点处于一种“寻路性价比”低的状态，此类节点对路径寻优的实用度和可靠性偏低。传统蚁群算法采取初始信息素均匀分布策略，因此ηij是蚁群在初期状态转移过程中的唯一根据，所有节点的被搜索概率差异小，令蚁群初期搜索范围遍布全局，使得面对路径规划实际应用时，蚁群在搜索初期会不可避免地耗时搜索于“低性价比区域节点”，形成初期搜索存在盲目性和初期收敛速度较慢等问题[11-13]。因此文献[8]提出一种初始信息素差异化处理，以起点与目标点连线作为基准线，以各节点到该基准线的距离作为参考来对初始信息素进行差异化分布，越靠近基准线的节点的初始信息素浓度越高，由此即可形成范围性非均匀信息素对比，令蚁群在路径规划的初期搜索过程中倾向于靠近寻优效益性价比高的范围内搜索，避开低效益区域，可在搜索初期耗时更短地规划出可靠性更高的较优路径以作后续搜索参考。文献[8]所设差异化区域在遇到地图环境中心存在较大障碍物或障碍环境繁密复杂以及存在U型障碍区间等情况时，部分处于差异化区域内经过初始信息素浓度增强处理的节点，反而会影响蚁群路径搜索的效果，造成路径多弯折的问题。基于此本文提出在目标点附近设立导向区作为改进，并对该优化区内的初期信息素给予一定的增强，为蚁群的初期搜索起到引导作用，有效降低初期搜索盲目性。根据地图信息，对地图进行矩形分块处理，以目标点E为圆心，R为半径的圆周范围设立为目标点导向区，计算方式如式（7）、（8），增强导向区信息素浓度，信息素差异化分布规则如式（6）所示：

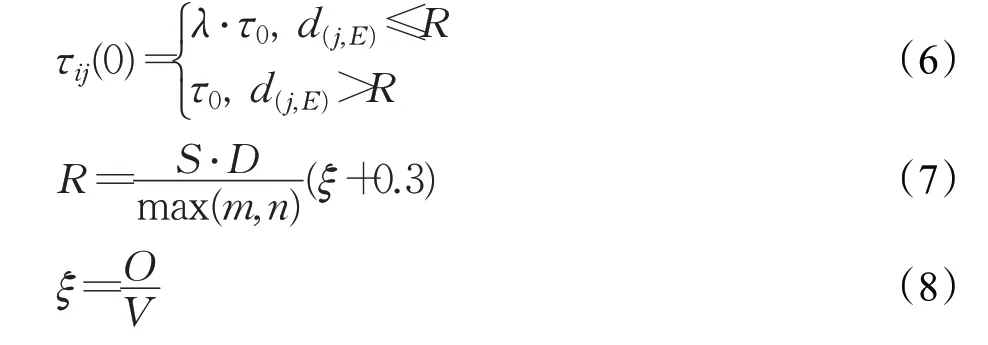
式（6）中，d(j,E)为节点j到终点E的欧式距离，τ0为初始信息素浓度，λ为[1，2]的初始信息素增强权值。式（7）中，S为矩形分块区边长值，D为起点至目标点的欧氏距离，m和n分别为栅格地图的长和宽，ξ为矩形分块区域内的障碍物占比，ξ值越大，则目标点导向区范围越大。式（8）中，O和V分别为矩形分块区内的障碍物数量和可行节点数。以20×20规模地图为例，取S=10进行分块，目标点导向区示意如图3所示。

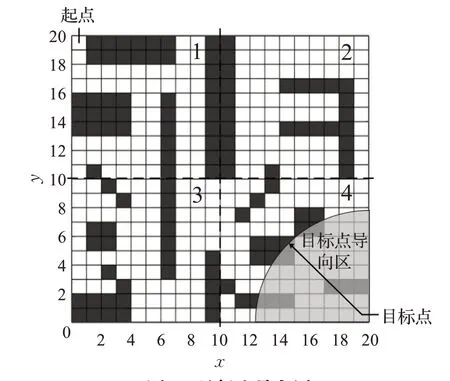
图3 目标点导向区Fig.3 Target point orientation area

如图3所示，将20×20地图进行分块后，以目标点为中心的扇形区域为目标点导向区，由此可形成初期信息素差异化，蚁群在初期搜索过程中，当节点搜索行径至2、3、4分块区时，会倾向于靠近4分块区的目标点附近范围搜索，避开2、3分块区的“低性价比”范围，并且受环境障碍因素的影响小，更快找到达到目标点的路径，减少初期搜索耗时。

3.2 局部路径分块优化

传统蚁群算法的评价函数以全局路径长度作为参考标准，从而忽视了对局部范围路径的好坏评价。如图4所示路径中，局部区域存在冗余折点状况，同时影响全局路径的长度评价。在移动机器人的实际工作环境下，多折点路线会对机器人的实体运动造成抖动、徘徊等负担。因此提出局部路径分块优化策略，对冗余折点状况进行改善。

图4 冗余多折点路径示意图Fig.4 Redundant multi-fold path schematic

对地图进行均匀的矩形划分，随后利用叉积运算依次检测多个折点与附近障碍物节点间的位置关系，若存在冗余折点则采取禁忌搜索结合回退策略，将折点暂时加入禁忌搜索冗余节点集并回退至折线段起始点，蚂蚁重新搜索路径并与最初原路径进行比较，经过循环多次检测、判断、比较后得出最终优化路径，局部折点优化示意如图5所示。

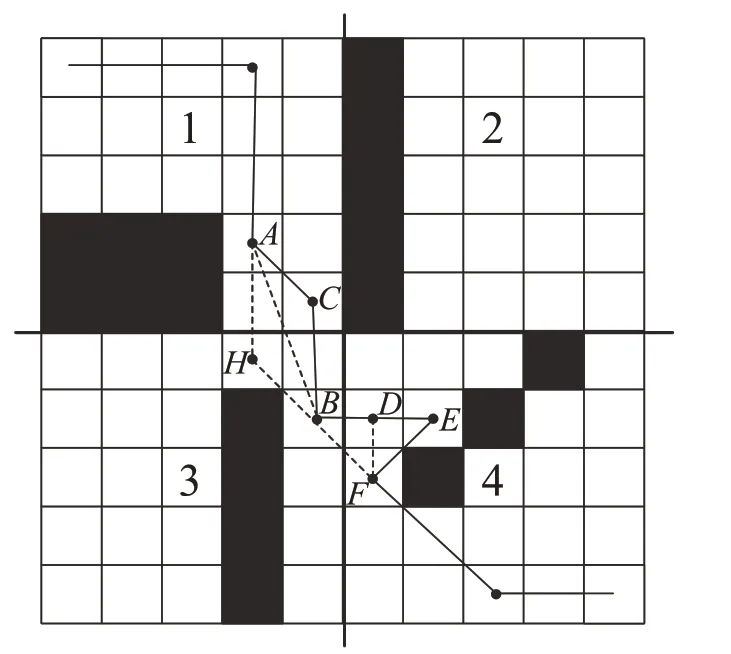
图5 多折点示意图Fig.5 Multi-fold diagram

图5路径中存在两处冗余折点，取S=5对地图进行局部分块，利用叉积运算检测，规则如式（9）所示：

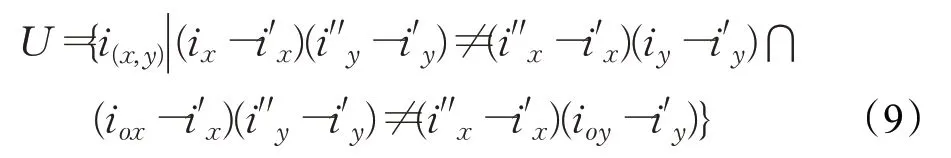
其中，U为冗余节点集，i为中间点，i′、i′为两端点，io为障碍节点。图4中，点A、C、B之间点A、C互为邻居节点位于分块1区，点B位于分块3区且AB连线无障碍节点，合并分块区通过叉积运算检测得C点为冗余节点，将点C暂时加入冗余节点集，蚂蚁回退至节点A重新搜索，经过反复循环对比获得安全路径“A-H-B”，同理可优化冗余节点D、E得路径“B-F”，最终完整局部路径为“A-H-F”，折点数与路径长度均比原路径“A-C-B-D-E-F”有较大改善。

将传统蚁群算法应用于20×20地图路径规划，进行局部优化前后对比，如图6所示。

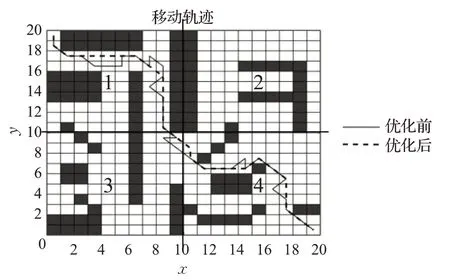
图6 20×20地图局部优化对比Fig.6 Comparison of local optimisation of 20×20 maps

由图6可知，原始路径折点数为25个，存在6处冗余折点，经过局部优化后的路径折点数为12个，仅存1处冗余折点，优化后路径更贴合机器人运动方式。

3.3 改进信息素更新机制

精英蚁群易受精英信息素的持续增强而过早陷入局部最优，因此提出一种随迭代次数增加而自适应调节的增强因子e(t)，起到各蚂蚁信息素之间的平衡作用。考虑到机器人需避开障碍物完成行径动作，提出一种随障碍物数量自适应的衰减因子，作为路段信息素增量的权重系数，改进的信息素更新公式如式（10）、（11）、（12）所示：

式（11）中，φ为(i,j)路段邻居节点集中障碍物的占比率，e(t)为自适应增强因子；式（12）中ω为[0,1]可选取系数，t为迭代次数。可知随障碍物数量增加，(1-φ)逐步衰减，降低相对应障碍物路段的信息素含量；随迭代次数的增加e(t)逐次降低，保障了初期精英蚂蚁影响力的同时降低后期的过度影响，有效避免蚁群过早陷入局部最优，增强全局搜索能力。

3.4 随机状态转移机制

传统蚁群的路径节点选取，只取决于Pk ij(t)的大小，迭代至后期，信息素浓度趋于稳定，高浓度信息素的路段被选取概率大，路径搜索出现停滞现象[14-16]。本文借鉴游晓明等人[17]提出的动态诱导策略，结合鲸鱼优化算法中的随机捕猎思想，提出一种随机状态转移机制，通过设置状态转移参数σ∈(0,1)和随机数μ=rand(0,1)对比，对蚁群的搜索状态进行调控，增加蚁群搜索机制的随机性，避免算法过早陷入停滞状态。随机状态转移规则为：当μ≥σ时，蚁群的状态转移根据Pk ij(t)轮盘赌策略决定，当μ＜σ时，蚁群根据式（13）、（14）更新下一路径节点位置。

其中，xt为当前位置点，x(t+1)为下一位移点，xτl为当前位置点所属邻居节点集中信息素含量最低节点，L为随迭代次数增长而下降的步长值。由式（13）可知，当μ＜σ时，蚁群被迫强制选取最差邻居节点并以一定步长位移。本文在移动机器人路径规划中采取式（15）作为路径评价目标函数。

3.5 算法步骤

本文改进蚁群算法的路径规划流程如图7所示。

图7 改进算法路径规划流程图Fig.7 Improved algorithm path planning flow chart

在改进算法中，实现路径规划的具体步骤如下：

步骤1初始化地图矩阵G、种群数量K、最大迭代次数tmax、初始信息素τ0、冗余节点集U、初始信息素增强系数λ、分块边长值S、D、信息素挥发系数ρ、ω、φ等参数。

步骤2根据式（6）、（7）、（8）和S值，对地图进行分块并设立目标点导向区，调整初始信息素。

步骤3将第k只蚂蚁放置于起始点。

步骤4根据随机状态转移机制与式（1）、（2）、（13）和（14）更新下一步位移节点。

步骤5判断是否达到目标点或陷入死胡同，若未到达目标点且未陷入死胡同转至步骤4；若陷入死胡同则回退至上一节点，并将当前节点加入禁忌表后转至步骤5重新判断；若已达到目标点转至步骤6。

为了验证所提控制策略的有效性,在PSIM环境下对MPDPC、定系数降频MPDPC和变系数降频MPDPC做了仿真对比研究,系统的参数如表1所示。为了简化,将上述3个控制策略分别依次定义为MPDPC.I,MPDPC.II和MPDPC.III。给定有功功率为1 000 W,给定无功功率为0 VAr,以保证系统单位功率因数运行。

步骤6判断是否所有K只蚂蚁已完成此次迭代中路径规划任务，若未完成则令k=k+1并转至步骤3；若均已完成则转至步骤7。

步骤7根据式（15）判断并记录每一代最优路径长及路线点。

步骤8根据分块优化策略及式（9）对每一代最优路径进行局部优化和全局整合，并记录对应节点信息。

步骤9根据式（10）和（11）更新信息素矩阵。

步骤10若迭代未满最大值，则令t=t+1,k=1，转至步骤3；反之转至步骤11。

步骤11输出全局最优路径和最佳适应度值。

4 仿真实验及数据分析

为了验证改进算法的有效性，搭建栅格地图进行实验，仿真实验环境：操作系统Windows 10（64 bit），处理器Core™i7-7700，CPU3.60 GHz，运行内存16 GB，仿真平台MatlabR2018b。

4.1 状态转移参数σ分析

为验证状态转移参数σ对本文改进算法在搜索方式及全局搜索能力方面的影响效果，本节在30×30地图中以传统蚁群算法为基础模型，仅引入随机状态转移机制，模拟文献[7]中参数仿真分析实验的控制变量方法等。控制如：蚁群数量K、迭代次数tmax、全局初始信息素浓度τ0、挥发因子ρ、信息素启发因子α、能见度启发因子β等参数值固定不变，依次改变σ的取值为{0.1，0.3，0.5，0.7，0.9}，进行五种情况下的分批多次实验，观察σ取值不同时对蚁群搜索的影响效果，并根据实验结果选取出σ的合适取值。其余参数固定取值如表1所示。

表1 仿真参数Table 1 Simulation parameters

随机状态转移机制仿真结果如图8所示。

图8 σ取值不同时蚂蚁搜索路径Fig.8 Ant search path whenσtakes different values

由图8可知，当σ取值过大时，蚁群的搜索路径过于发散；当σ取值过小时，蚁群搜索能力受限，验证了σ对蚁群搜索范围可调控的有效性，综上考虑取σ=0.3作为参数设定值平衡改进算法的全局搜索能力与收敛性。

4.2 算法仿真对比

传统蚁群算法遵循标准蚁群的搜索机制，在初期搜索范围遍布全局，初期蚁群的搜索方向无引导性，收敛速度慢；文献[8]采取以始末两点基准线为参考的初始信息素差异化分布，提升收敛速度，但最终路径搜寻效果易受地图中心区障碍或U型障碍环境影响；樽海鞘群算法以领导者结合追随者的更新机制寻求目标函数的最优问题，该算法中采取随机位置更新机制系数c3来决定位置更新方向和随机步长系数c2来决定移动长度。为验证本文改进算法中初始信息素差异化策略、折点优化策略及随机状态转移机制在路径规划应用中的综合效果，将本文改进算法与传统蚁群算法、樽海鞘群[18]算法及文献[8]改进算法分别在30×30和50×50地图中进行路径规划的实验对比分析，验证算法收敛速度、路径长度及路径弯折提升的有效性，仿真参数如表2、3所示。

表2 30×30地图仿真参数Table 2 30×30 map simulation parameters

表3 50×50地图仿真参数Table 3 50×50 map simulation parameters

4.2.1 简单环境30×30地图实验对比

在障碍物占比率为20%的30×30地图中，实验结果如图9、图10所示。

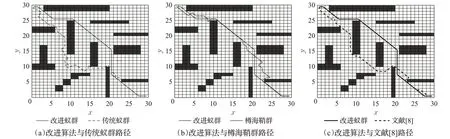
图9 简单环境30×30地图路径对比Fig.9 Comparison of 30×30 map paths in simple environment

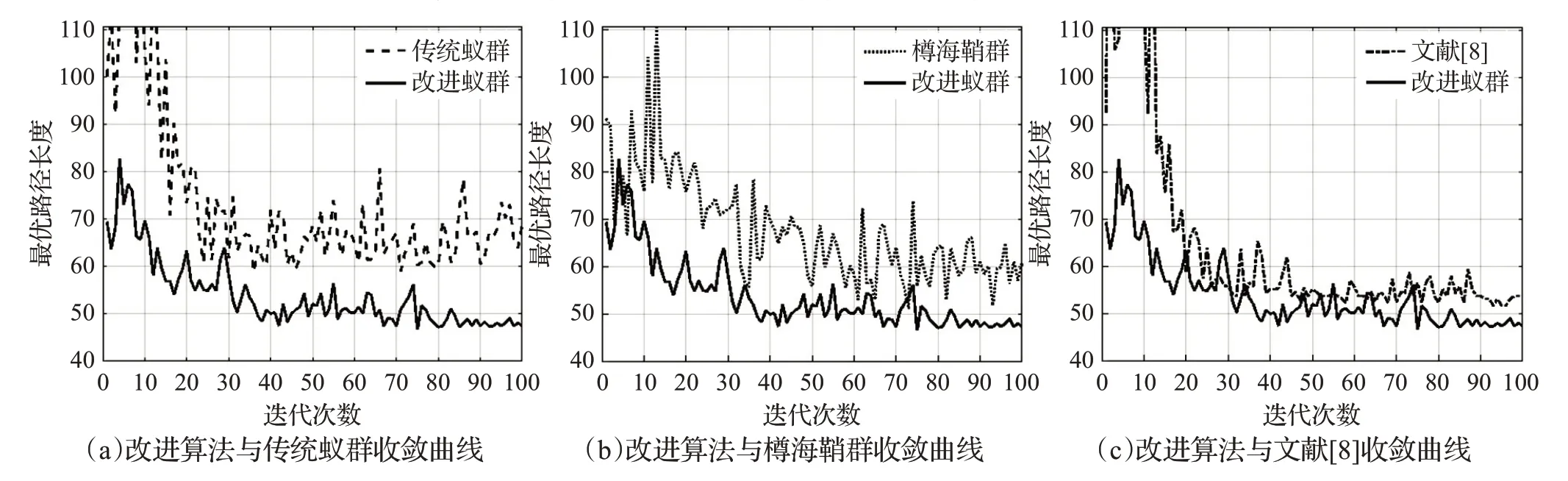
图10 简单环境30×30地图收敛曲线对比Fig.10 Comparison of 30×30 map convergence curves in simple environment

由表4可知：在30×30简单环境地图中，由于障碍物占比率低且分散，蚁群可探索范围空旷且可探索节点数多，传统蚁群和樽海鞘群因初期搜索无方向引导性，导致在面对可搜范围空旷的环境下收敛速度慢，最终未能实现完全收敛；文献[8]算法与本文改进算法在迭代次数达到90～95时呈逐渐收敛趋势。本文改进算法拐点个数比传统蚁群和樽海鞘群分别减少了82%和70%；路径长度分别缩短了31%和22%。文献[8]采取初始信息差异化分布，并采用排序择优方式更新信息素浓度提高收敛速度，但初始搜索范围会偏向于始末点间的连线狭小区域，且在后续信息素更新中该趋势逐步增加，如图9（c）中路径对比可知，当地图中央区域存在有较大障碍物使得起点和目标点连线区形成阻断形势时，文献[8]的搜索效果受到干扰，出现向中心线靠近的多折点现象。而本文改进算法在引入目标点导向区范围的初始信息素差异化分布后，对比传统蚁群在收敛速度方面有所提升，且应对此类中间区存有障碍物阻断的地图环境中有较好效果，本文改进算法的路径长度虽仅比文献[8]路径缩短12%，但拐点个数比文献[8]减少了62%，本文改进算法应对地图环境抗干扰性有所提高，折点优化效果良好。

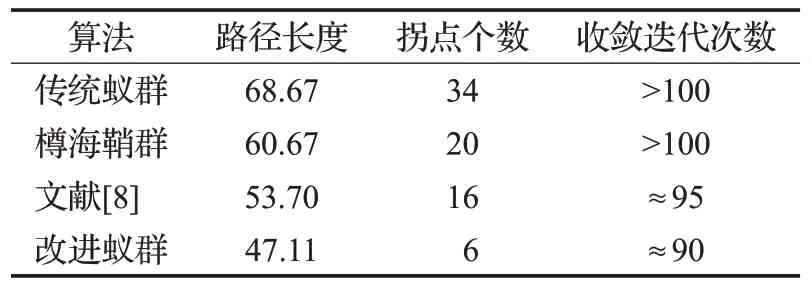
表4 简单环境30×30地图数据对比Table 4 Comparison of 30×30 map data in simple environment

4.2.2 复杂环境30×30地图实验对比

在障碍物占比率为23.77%的30×30地图中，实验结果如图11、图12所示。

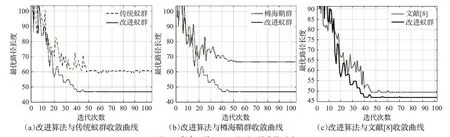
图12 复杂环境30×30地图收敛曲线对比Fig.12 Comparison of 30×30 map convergence curves in complex environments

由表5可知：在30×30复杂环境地图中传统蚁群和樽海鞘群分别在迭代次数达到95次和52次后趋于完全收敛，本文改进算法与文献[8]均在迭代至约46次实现完全收敛，本文改进算法在路径规划应用中，收敛速度方面对比传统蚁群采取初始信息素均匀分布策略有较大提升；路径长度平均缩短约24%，拐点数平均减少约53%。由图11（b）观察得，在面对复杂环境下，本文改进算法的随机状态转移机制对比樽海鞘群算法中的随机移动步长结合随机移动方向机制，樽海鞘群因搜索过度随机而出现路径回环，而本文改进算法在迭代次数与其相近的条件下，良好地避免了路径回环及死锁的现象。由图11（c）观察得，文献[8]路径在复杂环境下仍受地图中心区障碍物阻断影响，在栅格图节点搜索中出现穿越障碍物状况，本文改进算法受地图障碍干扰性小，路径长度、迭代次数与文献[8]相近的情况下，拐点个数更少且路径良好完成了避障效果。

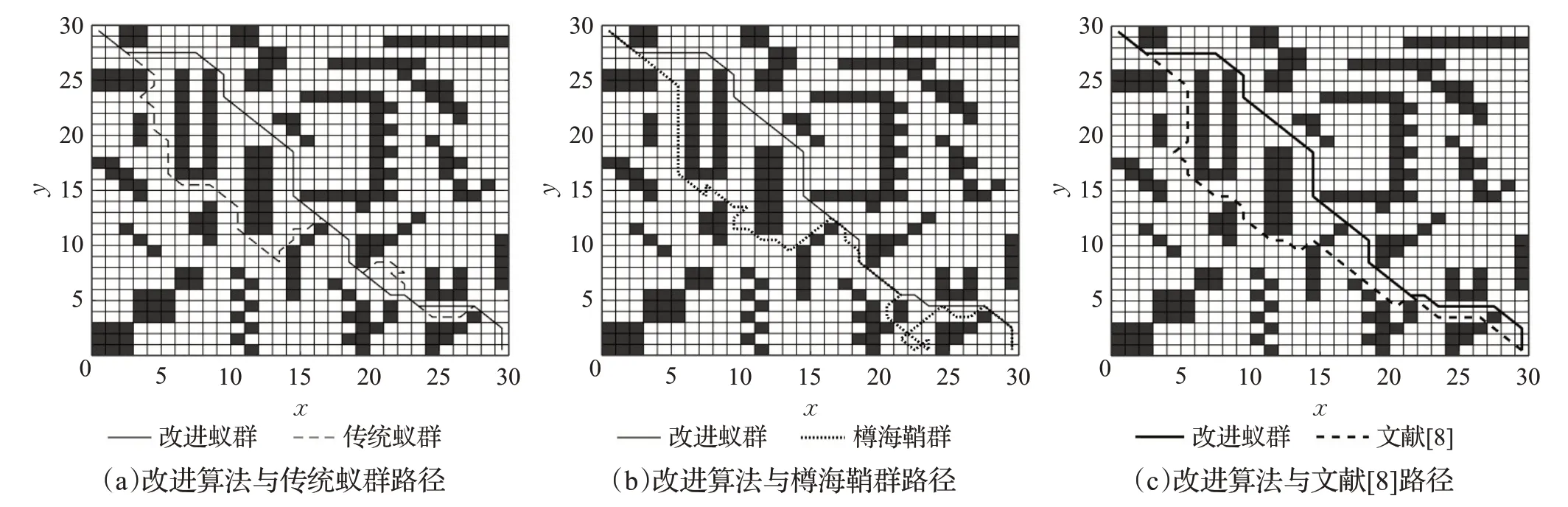
图11 复杂环境30×30地图路径对比Fig.11 Comparison of 30×30 map paths in complex environments

表5 复杂环境30×30地图数据对比Table 5 Comparison of 30×30 map data in complex environments

4.2.3 50×50地图实验对比

在障碍物占比率为23.24%的50×50地图中，实验结果如图13、图14所示。

图13 50×50地图各算法路径对比Fig.13 Comparison of 50×50 map paths of algorithms

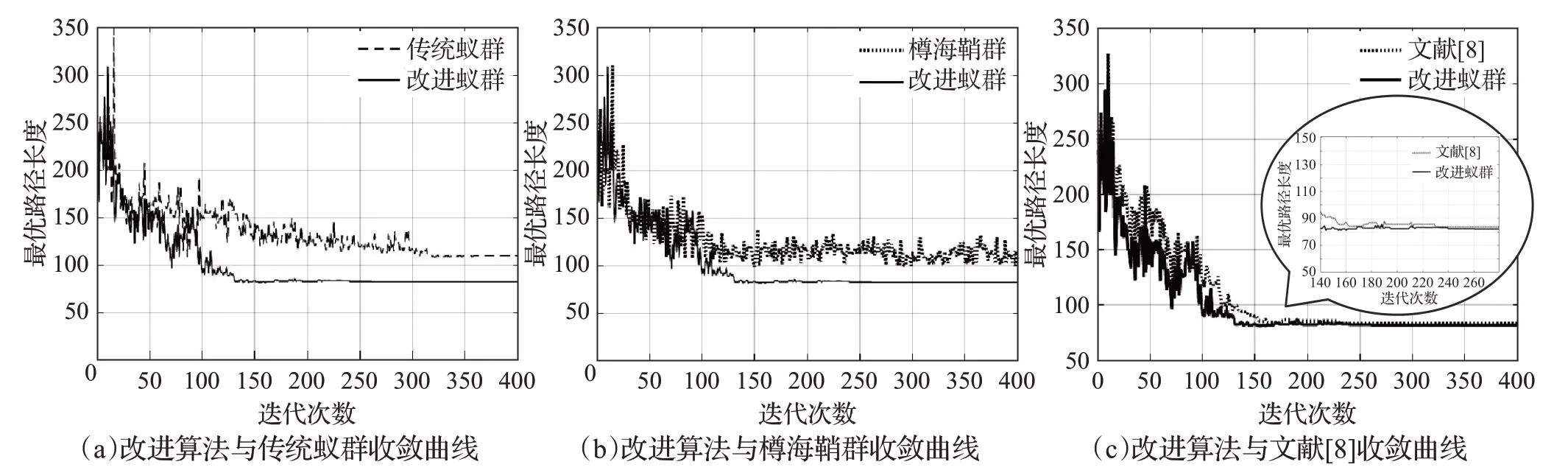
图14 50×50地图各算法收敛曲线对比Fig.14 Comparison of 50×50 map convergence curves of algorithms

由表6可知：在50×50地图中，本文改进算法在收敛迭代次数方面比传统蚁群和樽海鞘群平均减少45%；在拐点数方面平均减少81%；在路径长度方面平均减少21%。在50×50复杂环境下，传统蚁群与樽海鞘群初期搜索方向均无引导性，遍布全局地图，致使收敛速度慢，樽海鞘群因随机移动方向和随机移动步长机制以及随机参数取值问题，导致在复杂环境下，路径的后期搜索未实现最终收敛。本文改进算法通过初始信息素差异化加快了算法初期收敛速度，并由随机状态转移机制和对随机因子σ的取值分析，较好地平衡了搜索随机性与算法收敛性。本文改进算法与文献[8]的收敛迭代次数和路径长度方面均相近，但在50×50的复杂环境地图下，由图13（c）可知，障碍物不规则的复杂环境对文献[8]算法的实现存在干扰性，面对U型障碍区和对角相邻特征的障碍存在回拐和穿越等现象。本文改进算法在路径搜索过程中较好地完成了对U型区及复杂邻接障碍的避障效果，完整路径的拐点个数比文献[8]减少约58%。

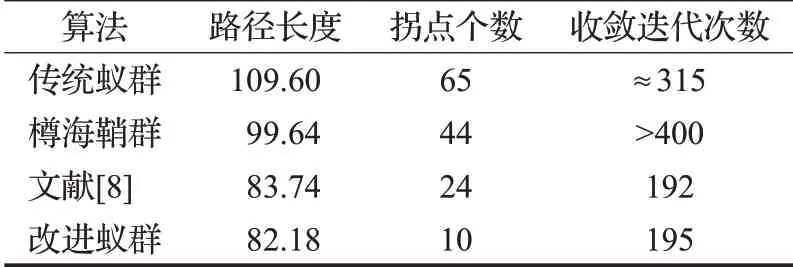
表6 50×50地图数据对比Table 6 Comparison of 50×50 map data

5 结语

在传统蚁群算法中初期搜索存在盲目性，本文提出设立目标点导向区形成初始信息素差异化分布，为蚁群初期搜索提供向目标点移动方向的参考导向，且导向区范围影响力随环境因素变化而改变，并非固定比例的类椭圆型优化区，避免了蚁群搜索偏于向地图中心靠拢，为蚁群指引目标方向的同时也具有一定的搜索随机性和寻优能力；改进最优路径信息素增强因子为随迭代次数变化的自适应调节因子，并引入随机状态转移控制参数及邻居节点转移规则，解决传统蚁群算法初期搜索收敛慢的同时避免算法中后期过早收敛陷入局部最优；引入局部分块优化策略结合叉积运算规则，改善算法规划路径产生的冗余节点，使得在面临地图环境大、障碍分布复杂及存在类U型障碍和邻接障碍集的情况下，规划出可有效避障且折点数少的最优路径，更符合移动机器人运动方式。最后，通过在多种地图下与其他算法（传统蚁群、樽海鞘群、文献[8]改进算法）进行对比实验仿真验证了本文改进算法的有效性。