基于三维空间响应分布函数的脉冲中子孔隙度测井快速模拟

付新月 吴文圣 张恒荣 葛云龙 王 虎

1.中国石油大学（北京）油气资源与探测国家重点实验室 2.中海石油（中国）有限公司湛江分公司3.中国石油集团测井有限公司

0 引言

玻尔兹曼方程通常用来描述粒子在地层中的扩散运动。密度测井和中子孔隙度测井的物理过程可以用玻尔兹曼方程来描述，通过求解玻尔兹曼方程可以得到探测器的伽马和中子通量[1-2]。然而直接用数学方法求解玻尔兹曼方程非常复杂，通常都是通过增加先验条件来求解该方程[3]。与直接求解方法不同，蒙特卡洛方法可以通过跟踪每个粒子的运动历史来模拟探测器的粒子通量[4]。核测井响应的正演模拟大多用蒙特卡洛方法实现。这种方法精度高，可以设置三维地层和测井仪器模型并提供复杂的物质材料分布，能够准确模拟得到探测器的中子通量并计算中子孔隙度值。对于中子孔隙度测井，该方法可以模拟中子测井响应，分析不同地层和环境对中子测井的影响[5-8]，同时也用于测井仪器的设计，如优化源距、屏蔽体、分析探测器灵敏度等[9-11]。然而这种方法存在计算速度较慢、需要大量计算机资源的缺陷。尽管计算机技术的最新进展大大减少了蒙特卡洛模拟所需的计算时间，但仍然无法满足反演中所需要实时对比模拟测井曲线与实测曲线的要求[12]。

Watson[13]提出了用蒙特卡洛方法计算得到微分灵敏度方程来模拟岩性密度测井响应，成为快速模拟核测井响应的基础。Couet等[14]用灵敏度函数方法分析了超热中子测井仪器的空间响应，同时提出计算中子空间分布灵敏度函数的方法可以辅助测井仪器设计。Mendoza等[15-17]利用通量灵敏度函数和几种近似方法来求解玻尔兹曼方程，实现了传统化学源的核测井曲线的快速模拟。国外学者在核测井的快速模拟方法上做过一系列研究，国内对于快速模拟方法研究较少。葛云龙等[18-19]利用二维伽马空间响应分布函数实现了补偿密度测井曲线的快速模拟。目前国内在中子孔隙度测井曲线的快速模拟方面还没有公开发表的文献。同时在斜井的中子孔隙度测井中，不同方位地层不是各向同性，不同方位地层对探测器的贡献不同[20]，利用二维空间响应分布函数来模拟中子孔隙度测井曲线会带来一定误差。

为此，笔者提出了用中子的三维空间响应分布函数快速模拟脉冲中子孔隙度测井曲线。首先，利用蒙特卡洛方法计算单位地层对探测器计数的贡献即探测器的三维空间响应分布函数，考虑不同方位地层对探测器计数的影响，同时计算出不同地层条件下探测器的中子计数，建立不同地层的三维空间响应分布函数和探测器中子计数的数据库。通过单一地层不同探测器的中子计数与探测范围内地层对探测器计数的贡献叠加得到不同组合地层下探测器的中子计数，根据不同探测器的中子计数比与地层孔隙度的关系求取地层的中子孔隙度值，实现中子孔隙度曲线的快速正演模拟。

1 脉冲中子孔隙度测井快速模拟原理

1.1 探测器计数计算原理

在一定体积内中子的通量随时间变化率等于产生率减去泄漏率和吸收率，可以用玻尔兹曼方程来描述这一过程，如式（1）所示。等式左边第一项是粒子的泄漏率，第二项是吸收率；等式右边第一项是粒子碰撞转换率，右边第二项是粒子产生率[3]。

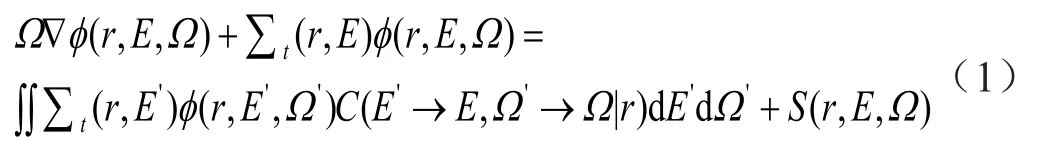
式中Ω、Ω分别表示中子的初始角度和碰撞后角度，（°）；φ表示能量为E、角度为Ω的中子通量，n/(cm2·s)；r表示空间中某一点与源的距离，cm；E、E分别表示中子的初始能量和碰撞后能量，MeV；∑t表示中子散射截面，1/cm；S表示源在单位时间内发射的粒子数，n/s；C表示中子发生散射的概率。

通过求解式（1），探测器的计数可以表示为每个从源发射的粒子对探测器贡献的总和[21]，如式（2）：

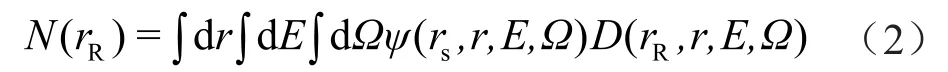
式中N（rR）表示探测器的计数，n；rs表示空间中源的位置，无量纲；rR表示空间中探测器的位置，无量纲；ψ表示位于rs处的放射源发射的中子在r处的通量，n/(cm2·s)；D表示rR处的探测器响应函数，与单位地层对探测器计数贡献的重要性和中子散射截面有关。

对于脉冲中子孔隙度测井，脉冲中子源发射的快中子与原子核发生非弹性散射、弹性散射反应，快中子能量降低变为热中子，探测器主要探测热中子。定义中子源发射的快中子经过几种作用后生成的热中子对探测器计数的贡献为中子的空间响应分布函数FN，如式（3）：

式中FN表示中子的空间响应分布函数，无量纲；w表示每个单位地层对探测器计数的重要性，即单位地层对探测器的贡献率。

空间响应分布函数定义为不同位置单位地层对探测器计数的贡献。利用蒙特卡洛方法计算得到不同位置单位地层的热中子通量和单位地层生成的热中子对不同探测器计数的重要性值[22-23]。利用空间响应分布函数结合参考地层探测器计数可以计算得到不同组合地层的探测器计数[18-19]。

如图1所示，可以将探测器计数视为探测区域内多套地层（地层B1、B2…Bn）对于探测器计数贡献的叠加。模拟时首先利用蒙特卡洛方法计算探测区域内各单一地层的近、远探测器空间响应分布函数作为背景空间响应分布函数，并分别计算得到各单一地层的近、远探测器热中子计数；然后在每个地层内对背景空间响应分布函数进行积分，得到每个地层对近、远探测器计数的贡献量。分别用每个地层的贡献量除以探测区域内所有地层贡献量的和得到不同地层贡献率，随后用相应地层的贡献率与模拟得到的单一地层近、远中子计数相乘后叠加得到综合地层的近、远探测器的计数，如式（4）、（5）所示。

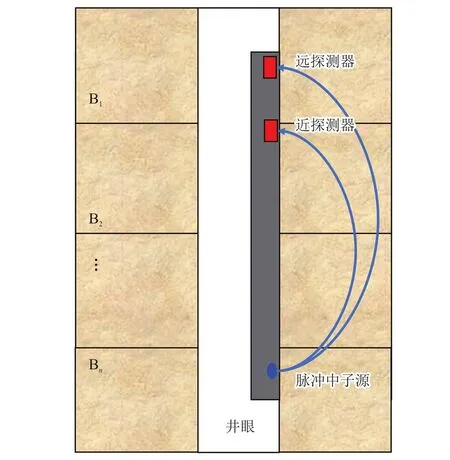
图1 脉冲中子孔隙度测井示意图

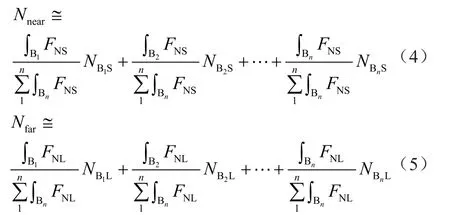
式中n表示地层数，套；B1、B2…Bn表示探测范围内第1套到第n套地层；Nnear、Nfar分别表示探测范围内近、远探测器的中子计数，n；FNS、FNL分别表示近、远探测器的空间响应分布函数，无量纲；分别表示模拟得到第n套单一地层的近、远探测器的中子计数，n。

1.2 中子孔隙度计算原理

脉冲中子孔隙度测井是通过建立近、远探测器热中子计数比与地层孔隙度的关系来求取地层孔隙度。根据双组扩散理论[2]，距离源r处的热中子计数如式（6）：

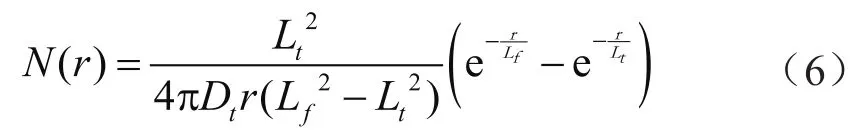
式中Dt表示热中子扩散系数，cm；Lf表示中子减速长度，cm；Lt表示扩散长度，cm。

近、远探测器计数比如式（7）：

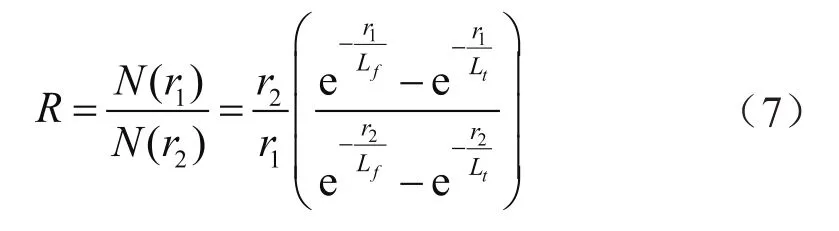
式中r1、r2分别表示近、远探测器与源的距离，cm。

对于热中子来说，扩散长度Lt很小，当r较大时，Lt可以忽略不计，因此式（7）可以写为：

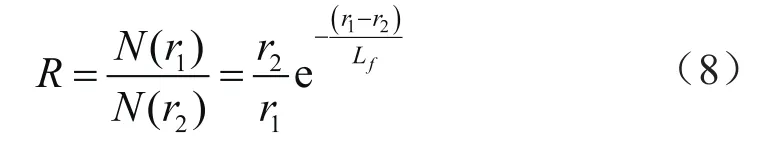
在仪器源距一定的情况下，中子计数比主要受减速长度影响，地层的减速长度主要与地层含氢指数有关。孔隙中的流体如水和油含氢指数较高，因此地层孔隙度的变化对中子计数比影响很大。可以通过建立中子计数比与孔隙度的刻度关系来计算地层中子孔隙度。

2 空间响应分布函数计算

地层的空间响应分布函数为单位地层的热中子通量与单位地层对探测器计数的重要性的乘积。利用蒙特卡洛方法分别计算单位地层的热中子通量与地层的重要性，进而得到不同地层的空间响应分布函数数据库。

利用蒙特卡洛方法建立三维地层模型，设置地层为圆柱体，高度为110 cm、半径为60 cm，井眼半径设置为10 cm，井眼流体为淡水、密度为1.00 g/cm3，地层中烃类气和油的密度分别为0.10 g/cm3和0.80 g/cm3。放射源采用脉冲中子源，发射能量为14 MeV，仪器包含两个He-3探测器，探测器长、短源距分别为65 cm和38 cm，源与探测器之间采用理想屏蔽体。地层分为9个扇区，靠近仪器的地层每30°设置一个扇区，仪器后部的地层每60°设置一个扇区。地层栅元在径向和纵向上的间隔为1 cm。三维模型如图2所示，图2-a为圆柱体地层的剖面、图2-b为圆柱体地层的横截面。

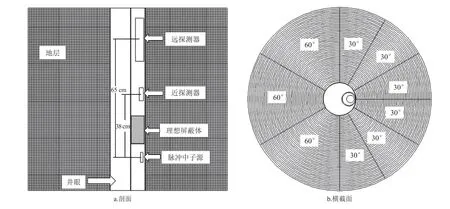
图2 蒙特卡洛地层模型图

设置地层为砂岩，地层孔隙度为10%，孔隙内为水，利用式（3）计算得到不同地层条件下的三维空间响应分布函数。计算得到的三维空间响应分布函数如图3所示。图3所示为空间响应分布函数沿x轴和井眼的切面，不同颜色代表单位地层对探测器计数贡献的大小。图3-a为远探测器的空间响应分布函数，图3-b为近探测器的空间响应分布函数。从图3可以看出，中子探测器计数主要由探测器附近地层所贡献，对近探测器有贡献的地层分布范围稍小，说明近探测器探测范围较小、探测深度较浅，对远探测器有贡献的地层分布范围广、探测深度大。井周向不同方位的地层对探测器计数贡献不同，探测器前部地层的贡献最大，探测器后部地层对探测器计数贡献很小。

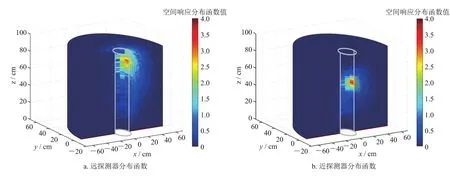
图3 三维空间响应分布函数图

通过图2的模型计算得到不同地层条件下单位地层的热中子通量与重要性。设置地层为砂岩，地层孔隙度为0、5%、10%、20%、30%、40%，孔隙流体为淡水和甲烷气体，模拟得到不同地层条件下的三维空间响应分布函数。不考虑不同方位角度地层的影响，将圆柱体横切面地层视为一个整体，对不同地层条件下的空间响应分布函数在纵向和径向上进行积分，结果如图4所示。从图中可以看出，当地层性质如孔隙度或孔隙内流体发生改变时，空间响应分布函数同时也发生变化。孔隙介质为水的地层空间响应分布函数值较大，孔隙度变化，含水地层的空间响应分布函数变化量较大；孔隙介质为气的地层空间响应分布函数值与纯砂岩地层的空间响应分布函数值相接近，孔隙度变化，含气地层空间响应分布函数变化量较小。不同地层条件下，空间响应分布函数的归一化几何因子也不同。利用不同的空间响应分布函数计算的近、远探测器计数有区别。快速模拟计算前，需要先建立不同地层条件下的空间响应分布函数的数据库以便于后续计算。

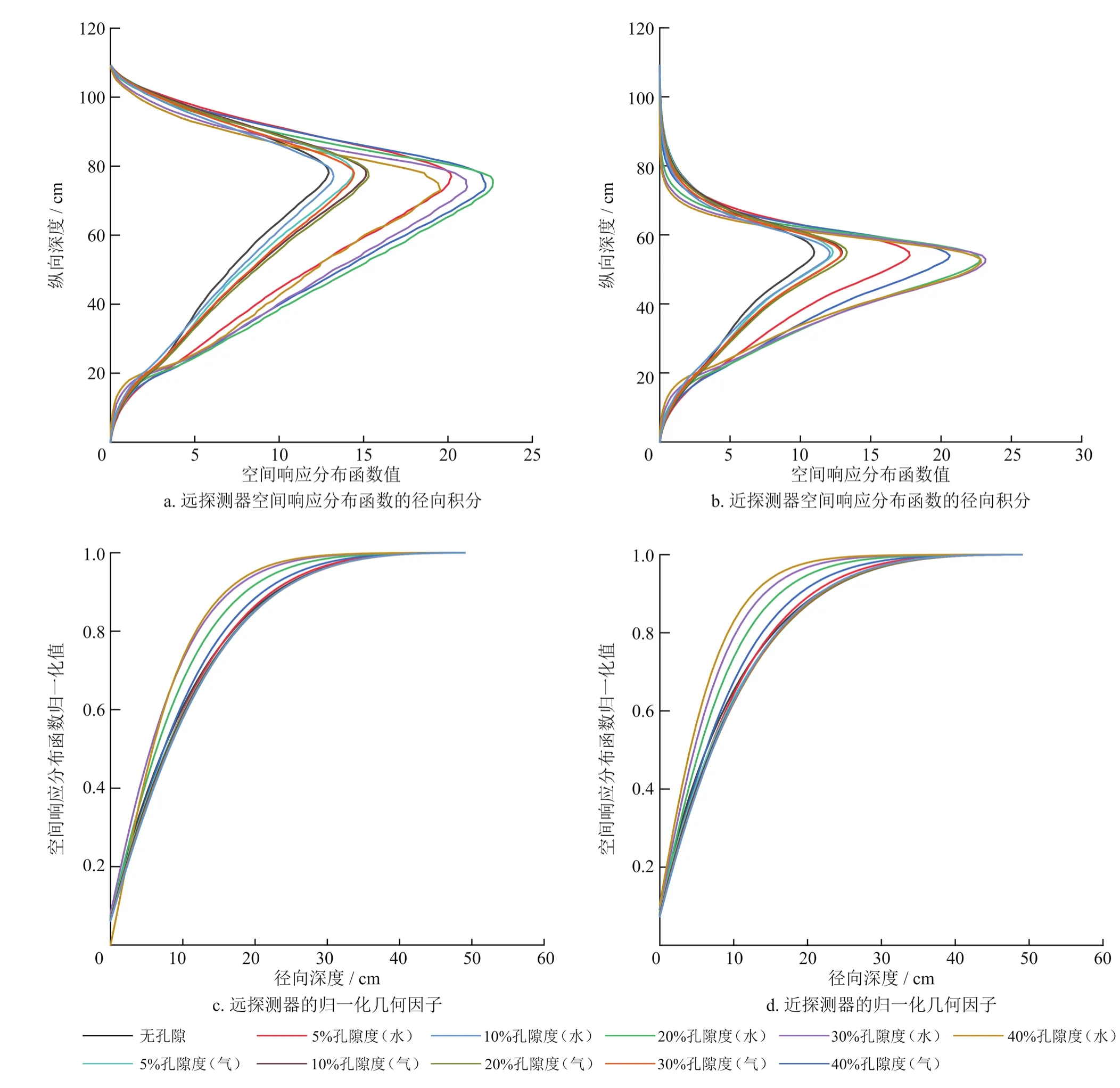
图4 不同地层条件下的空间响应分布函数图

3 中子孔隙度刻度公式

利用图2中的地层模型，模拟地层设置为单一地层，改变地层的孔隙度，分别模拟得到不同孔隙度地层的热中子计数比，建立中子计数比与孔隙度的刻度关系。设置地层为石灰岩，孔隙流体为淡水。地层孔隙度设定为0、5%、10%、20%、30%、40%。模拟中子计数比与孔隙度的关系如图5所示。

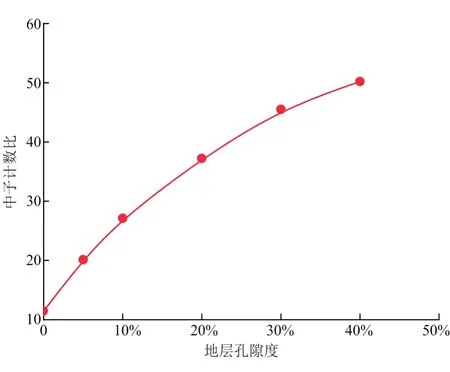
图5 淡水石灰岩中子孔隙度测井刻度关系图

对于淡水石灰岩地层，拟合得到地层孔隙度与中子计数比的关系，如式（9）：

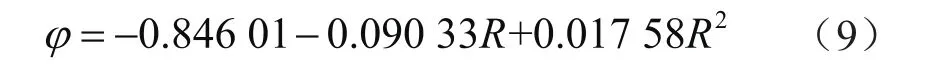
式中φ表示地层孔隙度；R表示中子计数比，无量纲。

计算中子孔隙度时，首先根据空间响应分布函数，利用式（4）、（5）计算得到近、远探测器计数比，然后根据式（9）计算出脉冲中子孔隙度值。

4 脉冲中子孔隙度测井正演模拟结果

4.1 直井中单一岩性地层的正演模拟

设置仪器探测范围内地层只有B1和B2地层，地层岩性均为砂岩且地层孔隙中为水，B2地层孔隙度为30%，B1地层孔隙度为5%，仪器自上而下运行，地层倾角为0°，以砂岩地层且孔隙度为10%时模拟得到的空间响应分布函数为参考，利用式（4）、（5）进行积分得到近、远探测器的计数，在通过式（9）计算出脉冲中子孔隙度值，得到的模拟结果与蒙特卡洛方法模拟的结果进行对比如图6所示，最大误差为 2.5 PU。

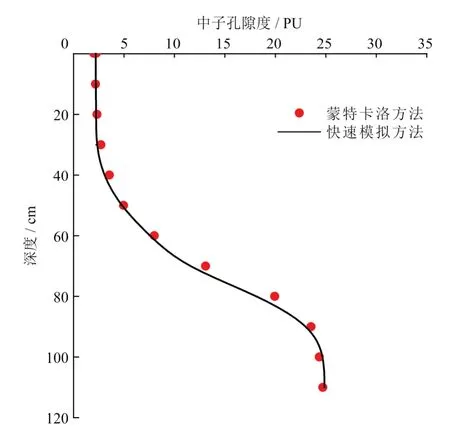
图6 直井快速模拟结果图

4.2 斜井中单一岩性地层的正演模拟

斜井的地层模型如图7-a所示。设置地层为含水砂岩地层，地层倾角为75°，地层孔隙度为10%，利用蒙特卡洛方法计算出倾斜角为75°的斜井的空间响应分布函数如图7-b、c所示。从图7中可以看出，斜井的空间响应分布函数与直井有较大差异，仪器后部地层对仪器的测量响应也有一定的影响。对于斜井的快速模拟需根据斜井的空间响应分布函数进行计算。

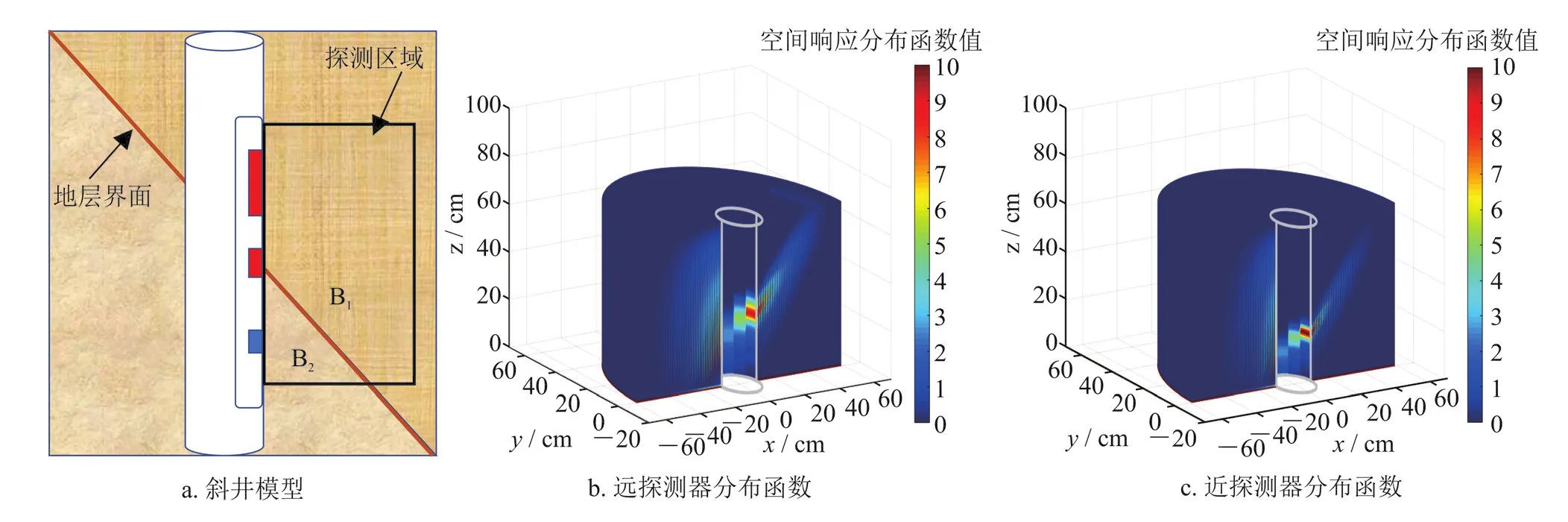
图7 斜井模型及其三维空间响应分布函数图

根据图7-a所示地层模型，开展斜井模型的脉冲中子孔隙度测井快速模拟。如图7-a所示，地层界面将仪器的探测区域分割成两个部分，设置上部地层孔隙度为5%、下部地层孔隙度为30%，地层为砂岩且孔隙中均为淡水。模拟仪器自上到下运行，参考的空间响应分布函数为75°斜井中10%孔隙度的砂岩地层的空间响应分布函数，利用式（4）、（5）计算不同探测器的中子计数，再通过式（9）将中子计数比转化为中子孔隙度值。在相同的地层模型下利用蒙特卡洛方法模拟得到长、短源距探测器的计数并利用式（9）转化成中子孔隙度值。对比蒙特卡洛方法模拟结果与快速模拟结果，得到结果如图8所示。

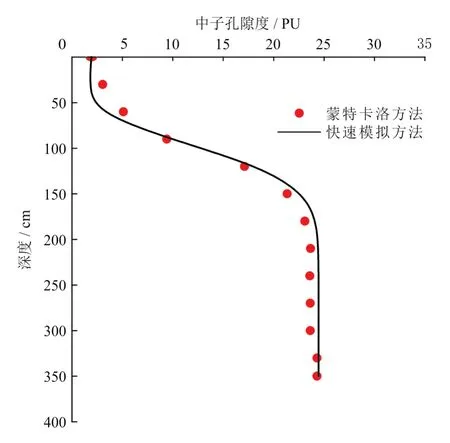
图8 斜井快速模拟结果图

从图6、8中可以看出，不管是直井还是斜井，快速模拟结果与蒙特卡洛方法计算结果基本一致，其中直井最大误差为2.5 PU，斜井最大误差为3.0 PU。在20核的服务器中蒙特卡洛方法模拟需要12 h，而快速模拟方法只需要十几秒，大大缩短了模拟时间。

4.3 多组地层模拟

设置每组地层厚度相等，地层岩性分别为砂岩、石灰岩、白云岩、泥岩混层，不同组地层模型的孔隙度不同，孔隙内流体为水、气和油，具体地层模型如表1所示，其中地层序号1～11、12～22和23～33分别代表砂岩、石灰岩和白云岩层。利用快速模拟方法和蒙特卡洛方法分别模拟不同地层条件下直井和75°斜井的脉冲中子孔隙度测井曲线，并对比快速模拟方法和蒙特卡洛方法的计算结果。模拟结果如表2所示。从表2中可以看出，快速模拟结果与蒙特卡洛模拟结果基本一致。含水石灰岩地层中的中子孔隙度计算结果与真孔隙度相等，含水砂岩地层的中子孔隙度小于真孔隙度，含水白云岩地层的中子孔隙度大于真孔隙度。当孔隙中含气时，由于存在挖掘效应，含气地层的中子孔隙度接近于0 PU；当孔隙中含油时，由于油的含氢指数低于水，油层的中子孔隙度略小于真实孔隙度；由于泥岩含氢指数较高，泥岩层的中子孔隙度大于真实孔隙度。

表1 多组地层模型中物质组分和性质参数表

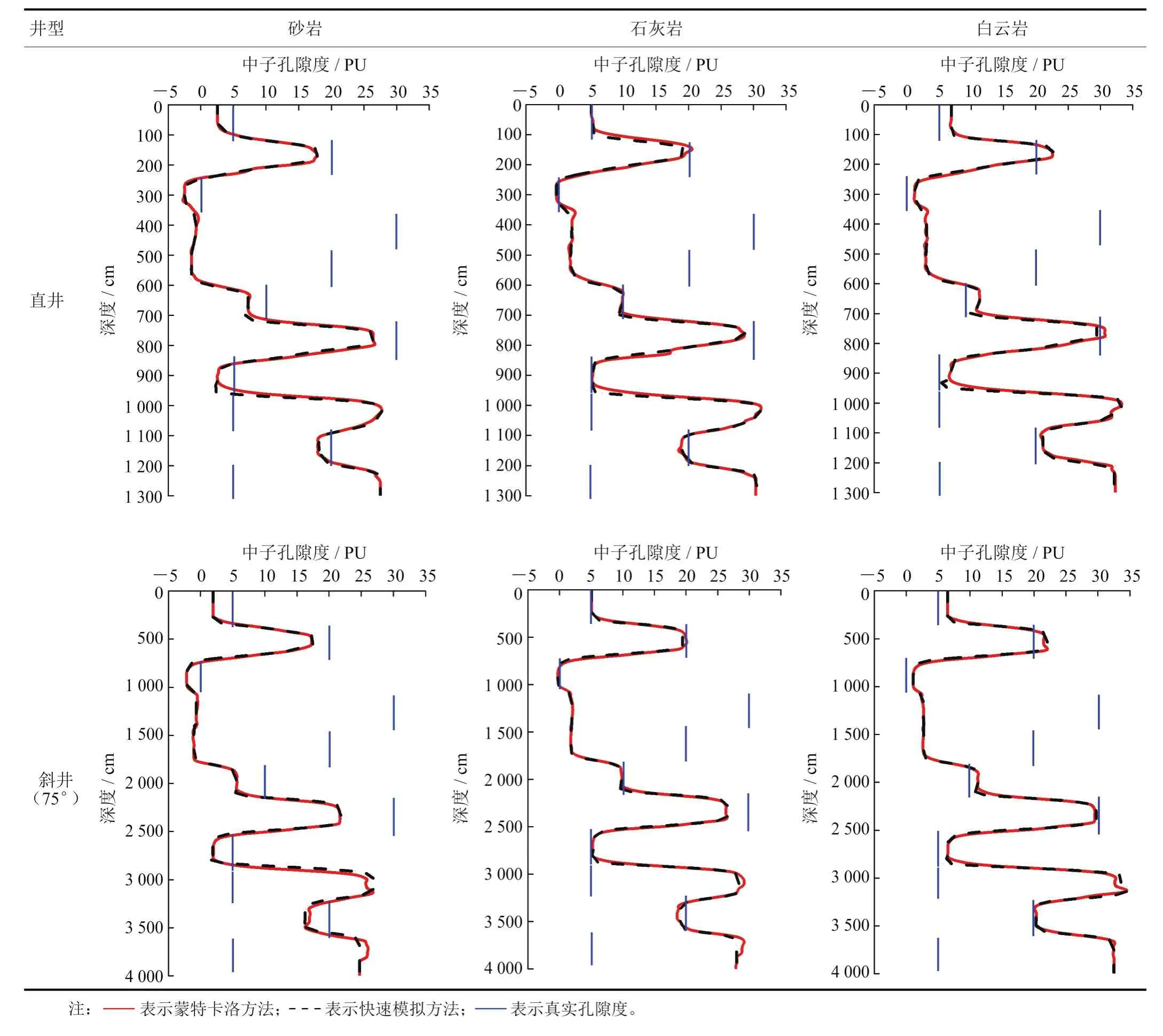
表2 不同岩性在直井、斜井中的地层快速模拟结果表

5 结论

1）利用中子的三维空间响应分布函数可以实现脉冲中子孔隙度测井曲线的快速模拟。通过蒙特卡洛方法模拟得到不同地层条件下的中子三维空间响应分布函数以及不同地层近、远探测器的热中子计数，建立一个包含三维空间响应分布函数和不同条件地层探测器计数的数据库。

2）对空间响应分布函数在不同地层区域进行积分得到不同地层区域对探测器计数的贡献。利用不同地层区域对探测器计数的贡献，结合预先模拟得到的单一地层近、远探测器热中子计数，计算得到不同组合地层探测器的热中子计数。然后，利用中子

计数比与孔隙度的关系得到地层的中子孔隙度曲线。3）与蒙特卡洛方法模拟结果相比，快速模拟方法结果在直井和斜井中最大误差分别为2.5 PU和3.0 PU。对于多组地层，快速模拟方法结果与蒙特卡洛方法模拟结果基本一致，可以满足中子孔隙度曲线正演需求。与蒙特卡洛方法花费时间几十小时相比，快速模拟方法仅用十几秒，大大提高了计算速度，为后续反演等应用打下了坚实的计算基础。