页岩油藏压裂水平井压-闷-采参数优化研究
2022-04-08陈志明赵鹏飞廖新维王佳楠
陈志明,赵鹏飞,曹 耐,廖新维,王佳楠,刘 辉
(1.油气资源与探测国家重点实验室(中国石油大学(北京)),北京 102249;2.中国石化石油工程技术研究院,北京 102206)
页岩油水平井压裂参数优化是一项极其重要的 研究工作。20 世纪40 年代开始,国内外研究了地层中流体的渗流机理[1],并在此基础上提出了井网部署的优化方法。例如,20 世纪80 年代初,童宪章院士[2]研究了水驱特征,提出了井网部署的优化方法。齐与峰等人[3]推导了井网影响采收率的理论公式,论证了合理井距的重要性。同时,随着数值模拟方法及油藏工程方法的应用和发展,学者们先后建立了人工裂缝诱导应力场模型[4]、分段压裂优化模型[5]、裂缝复杂性指数模型[6]、裂缝扩展模型[7-8]、闷井时间优化模型[9-10]及压裂缝间距优化模型[11],并提出了多种压裂参数优化及闷井时间优化的方法,为压裂参数优化研究提供了重要的理论基础。
鄂尔多斯盆地长庆油田非常规油气资源丰富,其中延长组长7 段烃源岩层系内发育页岩油资源[12-14],其资源量可达百亿吨以上[15]。页岩油藏开采难度大,与常规油藏相比渗流机理不同[16-18],需要改造储层提高储层渗流能力,目前主要采用水平井体积压裂方法开发[19-20],压裂技术发展迅速[21-23]。然而,在压裂、闷井和开采过程中,缺乏系统完善的参数(段间距、闷井时间和井距等)优化方法。因此,需要深入开展页岩油藏压裂水平井压-闷-采全周期压裂参数优化研究。针对这个问题,笔者以动态反演理论为基础,首先建立考虑页岩油储层特征和复杂天然裂缝的多段压裂水平井数值模型,得到油藏压力解及多段压裂水平井的瞬态压力数值解;然后,建立了段间距、闷井时间和井距等参数的优化方法,形成了一套页岩油藏压-闷-采全周期压裂参数优化方法,并进行了实例应用。
1 压裂水平井数学模型建立
1.1 物理模型
页岩油水平井经过大型压裂后,根据压裂效果分为不同区域:主力裂缝之间会形成复杂缝网,即缝网区,储层渗透率会显著增加;缝网区之外是受效区,即受压裂影响、渗透率有所增加的区域;受效区之外是不受压裂影响的未改造区,即原始储层,因此,物理模型包括压裂主裂缝、天然裂缝、缝网区、受效区及原始储层(见图1)。
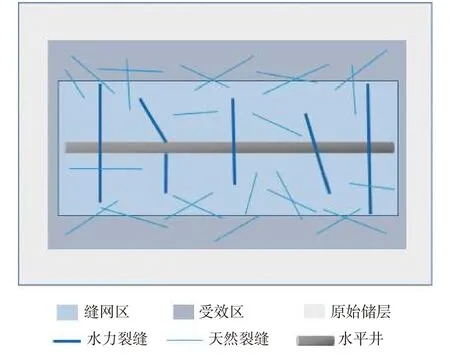
图1 页岩油藏多段压裂水平井物理模型Fig.1 Physical model of horizontal wells undergoing multi-stage fracturing in shale reservoirs
根据页岩油藏特性,假设页岩油藏压裂水平井模型满足以下条件:1)储层均质等厚,忽略储层垂向流动;2)裂缝简化为垂直平面,流体在裂缝中为一维线性流动;3)流体为单相流体;4)忽略重力等因素影响;5)油藏外部无渗透性;6)利用双重介质模型表征缝网区的裂缝网络系统和基质系统。
1.2 数学模型
页岩油藏中,基质中的流体流动方程为:
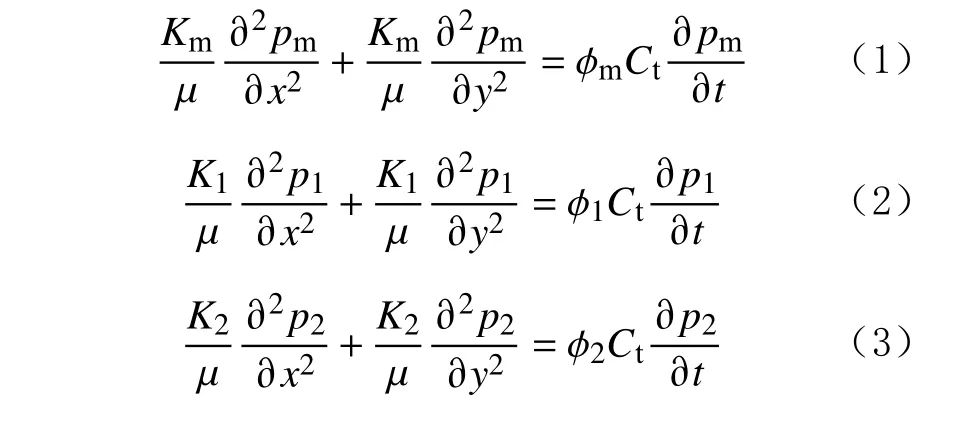
裂缝中的流体流动方程为:
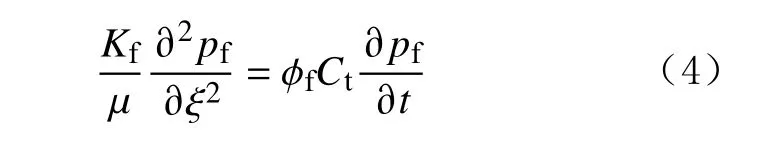
式中:Kf,Km,K1和K2分别为裂缝、缝网区、受效区及未改造区的渗透率,mD ;φf,φm,φ1和φ2分别为裂缝、缝网区、受效区及未改造区的孔隙度;pf,pm,p1和p2分别为主裂缝、缝网区、受效区及未改造区的压力,MPa;μ为流体黏度,mPa·s;Ct为综合压缩系数,MPa-1;x和y为全局坐标位置,m;ξ为裂缝局部坐标系(见图2[24])。
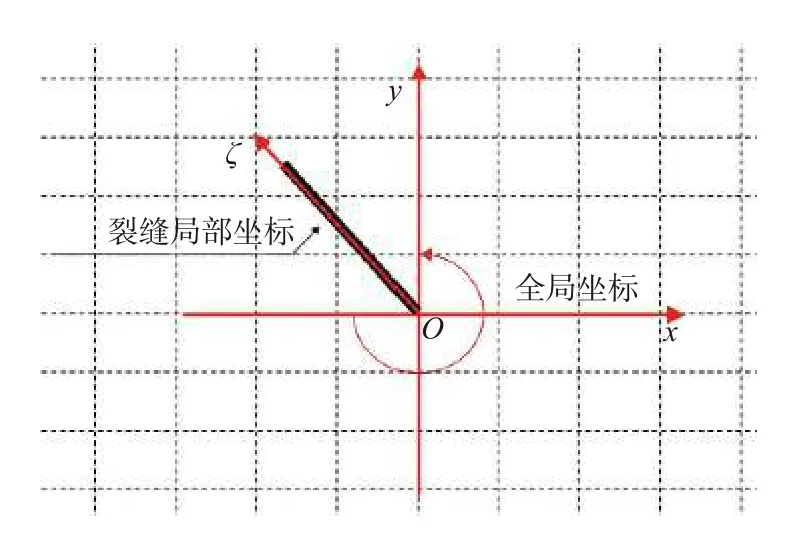
图2 全局坐标和裂缝局部坐标Fig.2 Global coordinates and local coordinates of fractures
建立多段压裂水平井EDFM-NM 数值模型,利用非相邻连接(NNC)来定义网格传导率[25],有4 种单元连接方式,分别是裂缝与裂缝、裂缝与基质、基质与基质和裂缝与井筒(见图3)。
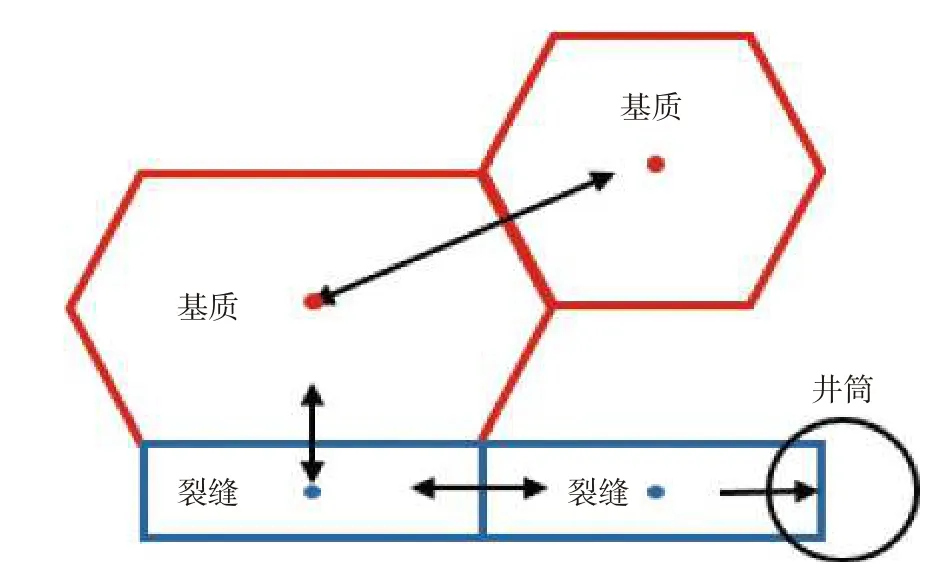
图3 单元连接方式示意图[25]Fig.3 Connection types of elements[25]
前3 种连接单元的传导率计算公式为:
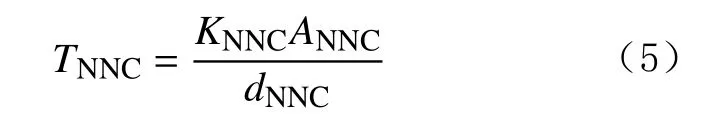
式中:TNNC为连接单元传导率,mD·m;KNNC为连接单元渗透率,mD;ANNC为连接单元接触面积,m2;dNNC为连接单元之间距离,m 。
第4 种裂缝与井筒单元的连接,根据Peaceman井模型的等效半径概念,考虑井储和表皮情况下的裂缝井有效井指数和产量的计算公式分别为:
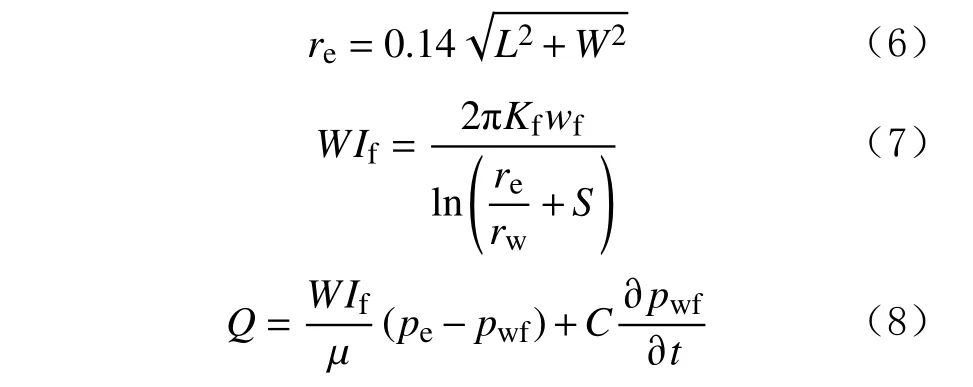
式中:rw为 井半径,m;wf为裂缝开度,m;L为裂缝单元长度,m;W为裂缝单元高度,m;WIf为裂缝井有效井指数,mD·m;pe为 井网格的压力,MPa;pwf为井底压力,M Pa;S为 表皮因子;C为 井筒储集系数,m3/MPa。
1.3 页岩油藏压裂水平井模型求解
基于自动微分原理,利用有限元方法对数学模型进行求解。首先,引进开源数值求解软件MRST程序[26]中的散度算子(div)和梯度算子(grad)简化求解过程,式(1)—(4)的全隐式离散形式为:
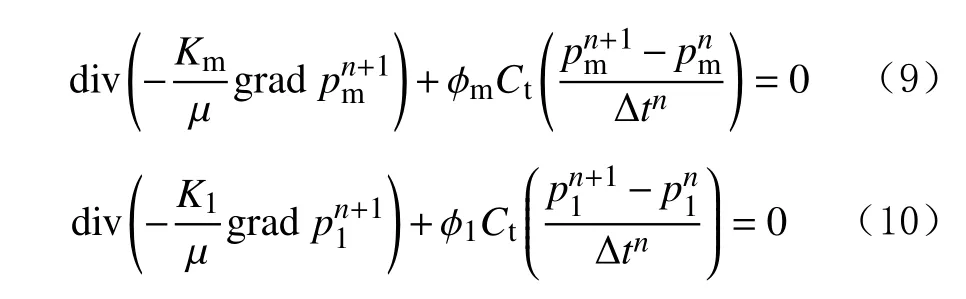
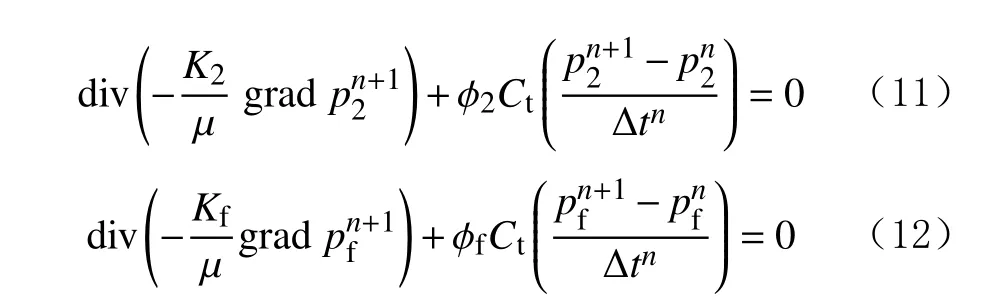
式(8)的全隐式离散形式为:
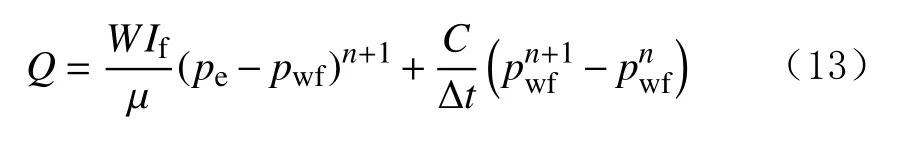
然后,利用自动微分技术和牛顿迭代原理,联合式(9)—(13),利用MATLAB 编程,即可求得数学模型的数值解(见图4)。
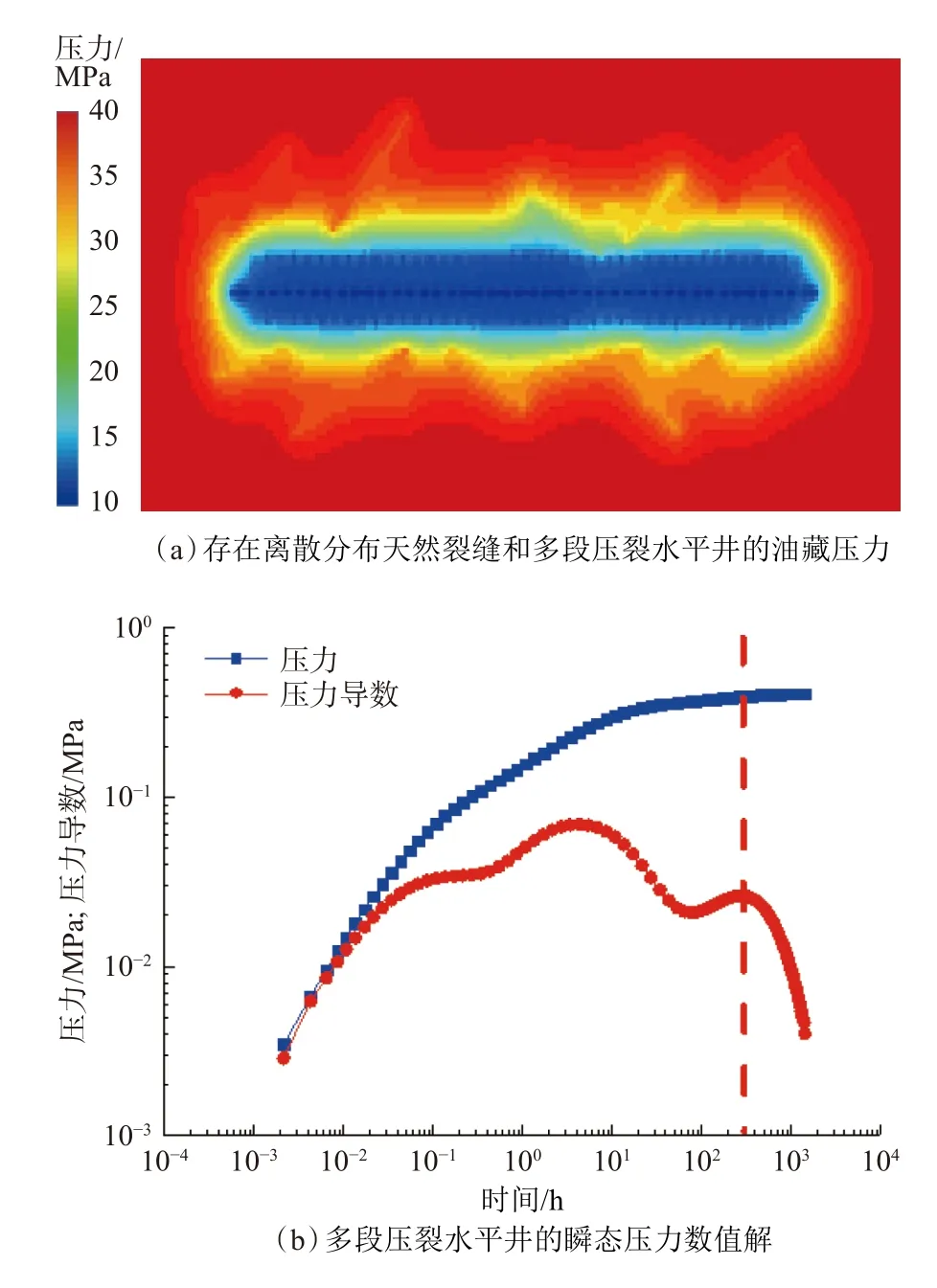
图4 数学模型的数值结果Fig.4 Numerical results of mathematical model
1.4 页岩油藏压裂水平井模型验证
为验证模型可靠性,将EDFM-NM 数值模型压力模拟结果与商业数值模拟软件KAPPA 数值模拟结果进行对比。由于商业数值模拟软件不易考虑天然裂缝,主要建立压裂裂缝模型进行验证。设置相距700 m 的2 口多段压裂水平井,裂缝26 条,将水平井周围地层划分为不同区域,区域地层参数及井参数如表1所示,定产量生产1 年,得到1 年后的地层压力分布状况(见图5)。从图5可以看出,EDFMNM 数值模型与商业数值模拟软件KAPPA 的压力模拟结果基本吻合;与商业数值模拟软件相比,EDFM-NM 数值模型模拟天然裂缝较为容易。
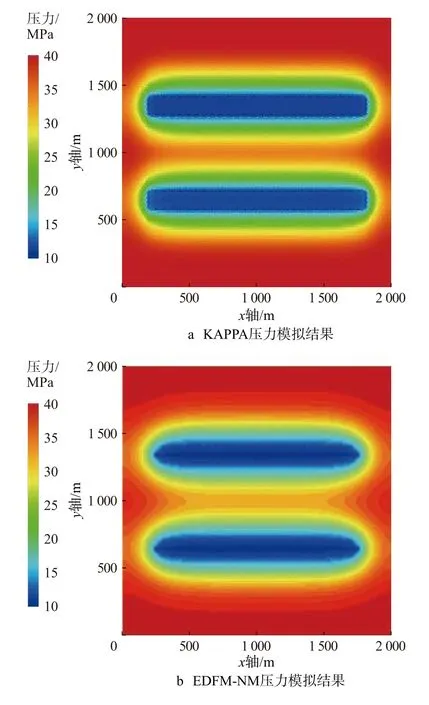
图5 页岩油多段压裂水平井模型可靠性验证Fig.5 Reliability verification of model for horizontal wells undergoing multi-stage fracturing in shale reservoirs
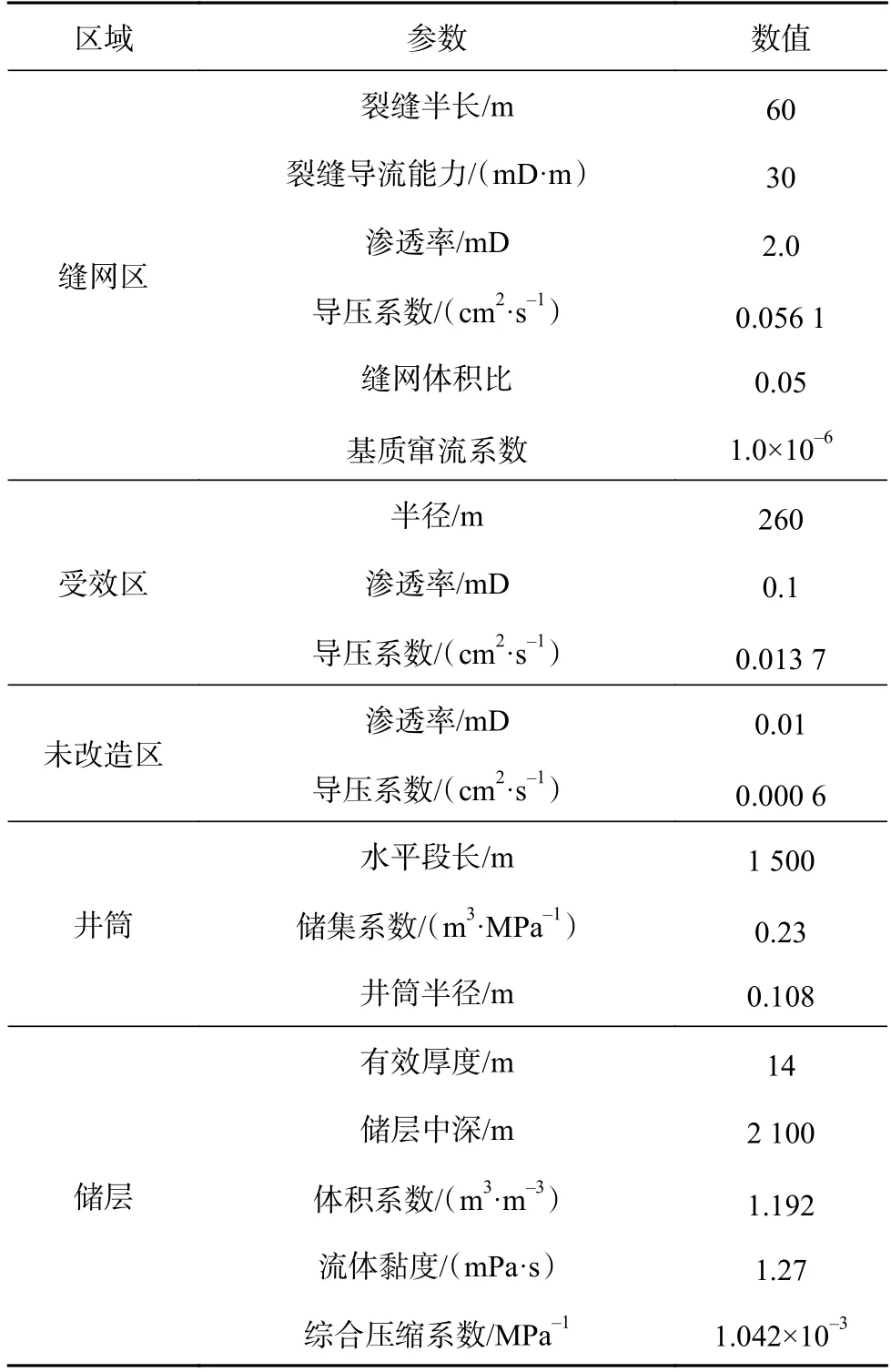
表1 长庆油田长7 页岩油XC 井基础参数Table 1 Basic model parameters of the Chang 7 shale oil well XC in Changqing Oilfield
2 水平井压裂参数优化方法
2.1 段间距优化
压裂过程中裂缝段间距是影响采收率的重要因素,段间距对页岩油藏的压裂改造效果具有很大影响。段间距过小,会导致主裂缝之间的改造效果重合,降低压裂改造效率;段间距过大,会导致改造不彻底,主裂缝之间留有未改造区,降低采收率。因此,需要开展页岩油压裂水平井的段间距优化研究。
首先,通过收集数据或生产历史拟合确定储层裂缝等基础参数,通过生产动态约束,提高解释结果的精确性;然后,基于建立的页岩油藏压裂水平井数学模型,构建不同段间距条件的数值模型,求得不同段间距的累计产油量;最后,绘制段间距与产油量关系图版,找到转折点,即水平井最优段间距(见图6)。
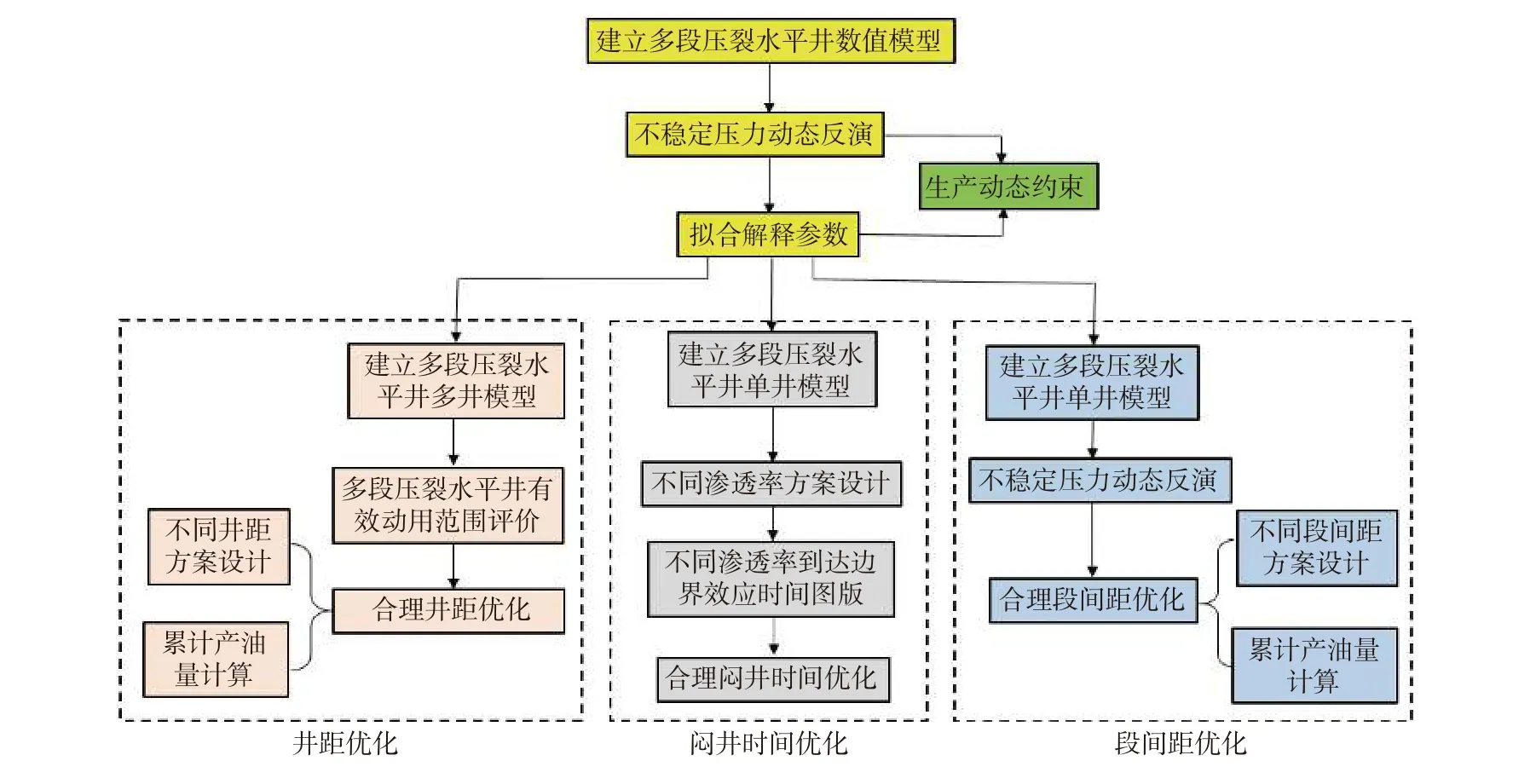
图6 页岩油多段压裂水平井压-闷-采全周期参数优化方法Fig.6 Multi-stage fracturing parameter optimization for horizontal wells in shale reservoirs during “well fracturing-soaking-producing”
2.2 合理闷井时间优化
随着闷井时间增加,水平井压裂过程中注入压力不断向外扩散传播。由于页岩油藏原始储层渗透率极低,压裂措施未波及区域基本表现为不渗透特性,当压力传播到该区域时,井底流压的导数出现下降的趋势(如图4(b)所示);井底流压变化率也趋于零,此时井底流压达到最小,生产压差达到最大。因此,合理闷井时间可定义为压力传播到单井最大控制范围所需要的时间。
首先,基于建立的页岩油藏压裂水平井数学模型,构建闷井条件下页岩油藏压裂水平井数值模型;然后,设计不同缝网区的渗透率,得到不同缝网区渗透率的试井曲线;最后,根据试井曲线得到不同渗透率的单井到达边界效应的时间,建立渗透率与边界效应时间图版。通过求取渗透率,查渗透率与边界效应时间图版就可得到最优闷井时间。
2.3 井距优化
首先,基于建立的页岩油藏压裂水平井数学模型,构建不同井距条件下页岩油藏压裂水平井多井数值模型;其次,设计不同井距方案,模拟多段压裂水平井井间压力传播范围,并计算不同井距下的累计产油量,绘制井距与产油量关系图版,利用该图版就能确定页岩油藏压裂水平井的最优井距。
3 实例应用
以长庆油田CQ 页岩油XC 井为例,首先,收集XC 井生产数据,进行生产动态分析;然后,利用长期压力产量数据进行不稳定产量生产动态约束,获取其基本参数(见表1);最后,将参数代入图7所示的模型,建立不同段间距、不同闷井时间及不同井距下的数值模型,利用敏感性分析进行参数优化。
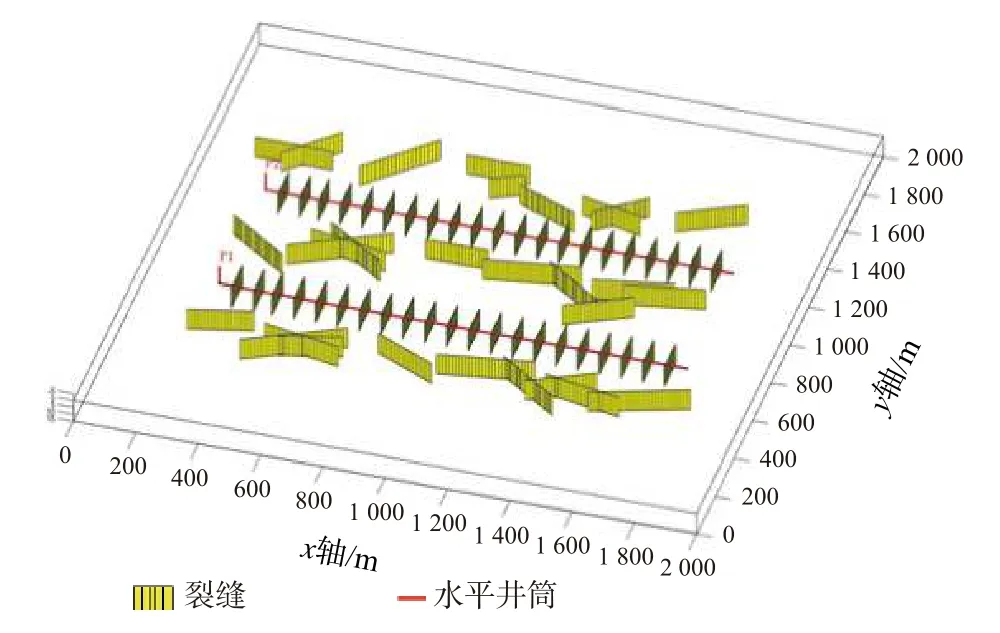
图7 XC 井多井模型示意图Fig.7 Multi-well model of Well XC
3.1 段间距优化
为了得到XC 井最优段间距,采用水平井压裂参数优化方法,设计裂缝数量分别为15,20 和30条,利用页岩油藏压裂水平井模型计算不同方案的累计产油量,分析累计产油量随段间距变化的规律。模型求解得到的不同裂缝段间压力波传播范围如图8所示。由图8可以看出,段间距小于100 m时,能够充分动用段间原油。

图8 不同段间距下裂缝间的压力分布Fig.8 Pressure distribution in induced fractures with different hydraulic fracture spacing
进一步设计裂缝数量分别为3,5,12,18,23,25,35 和40 条,计算不同段间距下的产油量,得到累计产油量与段间距的关系曲线(见图9)。从图9可以看出,段间距小于100 m 时,累计产油量的增长趋势趋于平缓。经过进一步分析,确定目前压裂规模下合理段间距为100~125 m。
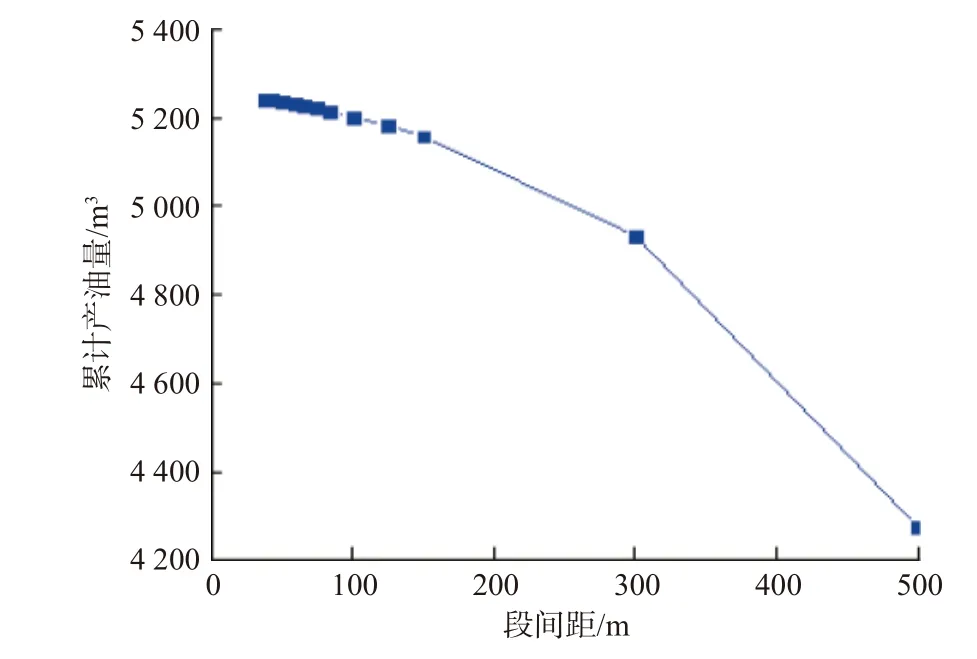
图9 不同段间距下的累计产油量Fig.9 Cumulative oil production with different hydraulic fracture spacing
3.2 闷井时间优化
以长庆页岩油藏压裂水平井XC 基本参数为基础,设计缝网区渗透率分别为1.2,1.5,1.8,2.1,2.5 和3.0 mD,利用页岩油藏压裂水平井模型,计算试井压力及其压力导数曲线,确定合理闷井时间。
统计不同缝网区缝网渗透率确定的合理闷井时间,绘制合理闷井时间与缝网区渗透率的关系曲线(见图10)。从图10可看出,随着缝网区渗透率增大,合理闷井时间缩短,二者近似为双曲函数关系。根据长庆油田CQ 页岩油藏压裂后缝网区渗透率分布范围,可得其合理闷井时间为25~35 d。
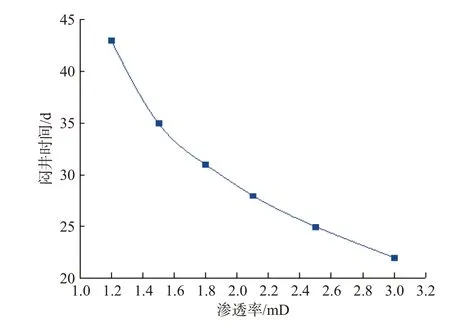
图10 合理闷井时间与缝网区渗透率的关系Fig.10 Relationship between proper soaking time and permeability in fracture network area
3.3 井距优化
以长庆页岩油藏压裂水平井XC 基本参数为基础,开展井间距优化研究。利用页岩油藏压裂水平井模型建立多井模型,计算得到井距为550 m 时不同生产时间的井底压力分布(见图11)。
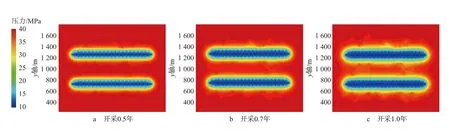
图11 井距550 m 时不同开采时间下的压力分布Fig.11 Pressure distribution at different stage of production with well spacing of 550 m
设两井井距分别为590,610 和700 m,利用建立的多井数值模型,计算得到不同井距下生产1.0 年的两井压力分布特征(见图12),分析井距与压力波传播距离的关系。
从图12可以看出,生产1.0 年时间后,地层压力波传播范围为590~610 m。进一步设置不同井距,利用建立的数值模型计算不同井距下生产1.0 年时的产油量,绘制年产油量与井距的关系曲线(见图13)。从图13可以看出,当井距大于590 m 时,年产油量的增加趋势开始放缓,井距为590 m 时的年产油量为5 130 m3,井距为525 m 时为4 570 m3,增加了12.25%。综合不同井距下的压力分布(见图12)和年产油量(见图13),得出XC 井压裂施工规模下的最优井距为590~610 m。
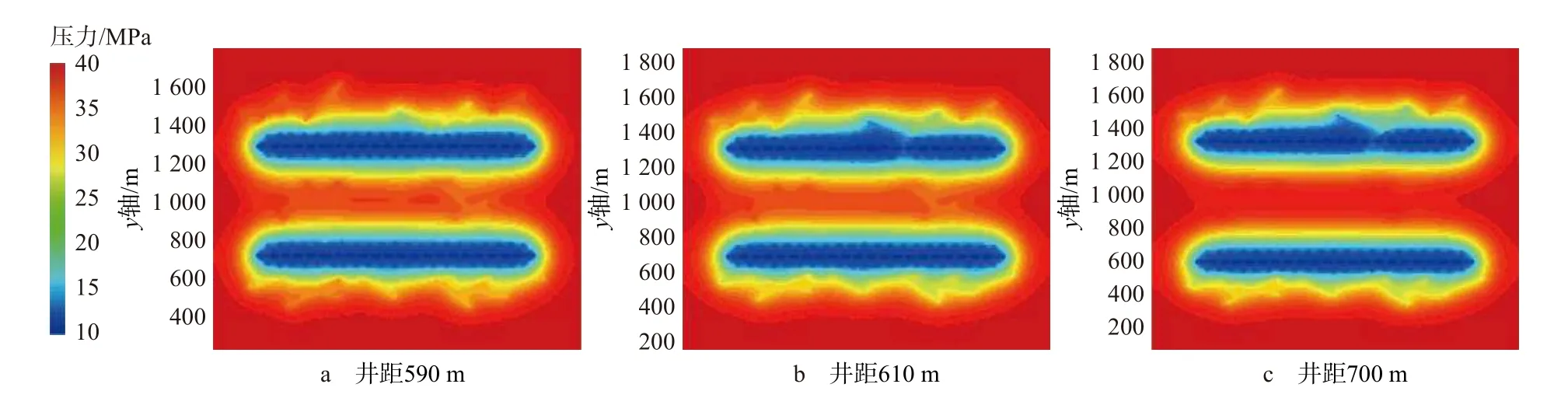
图12 不同井距下的多井数值模型压力分布Fig.12 Pressure distribution of multi-well numerical model with different well spacing
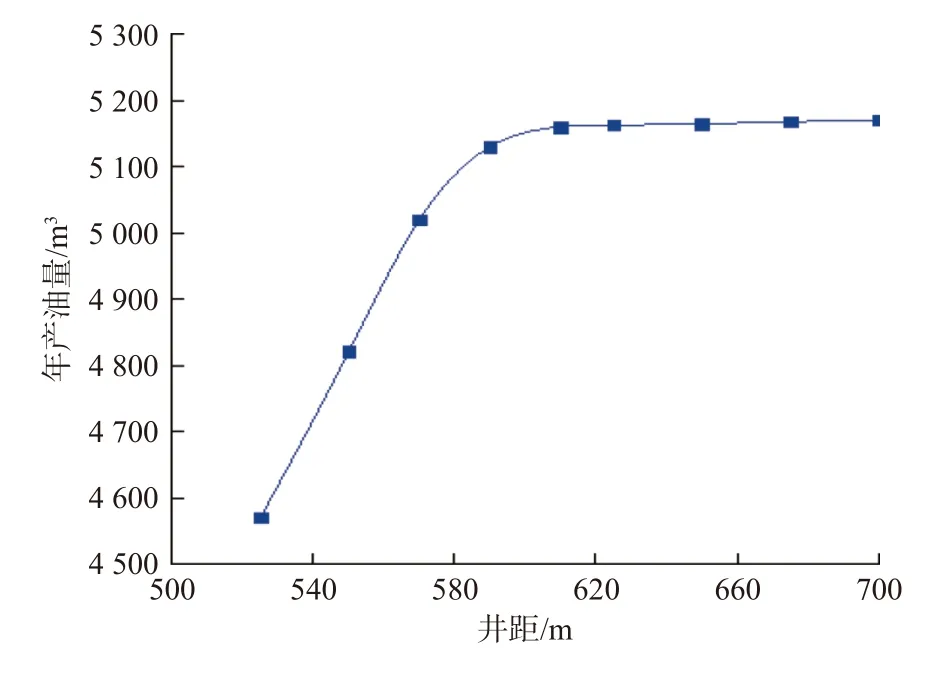
图13 不同井距下的年产油量Fig.13 Annual oil production with different well spacing
4 结论与建议
1)基于页岩油储层特征和缝网形态,推导了考虑主裂缝、天然裂缝、缝网区、受效区及未改造区的多段压裂水平井渗流数学模型,利用数值方法求解该数学模型,建立了针对于页岩油藏压裂水平井的数值模型及压-闷-采参数优化方法。
2)根据CQ 页岩油藏压裂水平井XC 井分析结果,可以得到累计产油量随段间距增长的变化趋势,合理闷井时间与页岩油藏缝网区渗透率两者呈近似于双曲函数关系,井距与累计产油量的关系曲线存在斜率转折点,由此可得到XC 井在现有压裂规模下的参数优化方案。
3)页岩油储层经过大型压裂后,井筒附近缝网系统复杂,模型考虑的条件不够充分,还需要根据不同页岩油藏储层物性继续进行压裂水平井参数优化研究。同时,还需要继续探究井距、段间距和闷井时间等参数与压裂规模之间的规律性。
