基于优化人工神经网络和TOPSIS的水利工程质量评价
2022-04-08徐超,李雁
徐 超,李 雁
(1.杭州富阳水利建设投资有限公司,浙江 杭州 311400;2.杭州市富阳区农业农村局,浙江 杭州 311400)
随着国内经济的快速发展,水利工程建设同样得到了快速的发展,我国水利工程的建设水平和建设质量同样得到了显著提高[1- 2]。由于水利工程相较于传统建筑工程有着施工周期长、投资大、影响广泛的问题,所以现如今水利工程的质量仍然存在较多问题,同时建设管理单位随着项目投资和周期的增大、工程低于跨度的增大,对水利工程的质量把控往往无法完全到位[3- 4]。因此,如何构建合理的水利工程质量评价体系,采用合理的方法对水利工程质量进行综合评价是保证水利工程质量的重要途径。
在以往的研究中,常采用主观打分、模糊评价等手段来综合评价工程质量。李玉红[5]基于模糊评价理论对农田水利工程建设质量进行了评价,基于层析分析法分析了不同影响因素的重要性,并构建了农田水利工程质量综合评价模型;杨大魁[6]基于模糊识别理论对水利工程质量进行了综合评定,通过计算不同指标权重,判定了水利工程综合等级为优良;张景奎、刘长顺[7]基于专家打分的层次分析法和模糊评价理论对小型渠系水利工程进行了评价,并验证了该方法的可行性。
随着现代信息技术的不断发展,一些机器学习算法已被广泛应用于工程综合评价中[8- 9]。但传统的机器学习模型参数寻优过程较慢,且易产生局部极值,导致对最终评价结果有所影响,需采用相关算法对模型参数迭代过程进行优化[10]。本文以人工神经网络模型(ANN)为基础,基于布谷鸟算法(CSA)、鲸鱼算法(WOA)和蝙蝠算法(BA)进行优化,实现评价体系不同层次指标自适应评价,基于TOPSIS模型实现水利工程质量总体评价,为水利工程日常管理提供理论指导。
1 评价体系构建
由于影响水利工程质量的因素众多,在选取评价指标时应遵循系统、科学和可操作性的原则。水利工程质量评价体系主要包括项目操作质量、项目管理质量和项目监理监督指标3个方面,具体评价指标体系见表1。
2 研究方法
2.1 人工神经网络模型
人工神经网络模型(ANN)已被广泛应用于事件评价中[11- 12]。ANN模型结构原理类似于人脑组织,由输入层、隐藏层和输出层组成,可经过数据收集、学习、适应、模式识别和定位5个步骤完成模型计算。本文采用反向传播算法来训练模型[13]。
2.2 蝙蝠优化算法
蝙蝠优化算法(BA)基于蝙蝠觅食行为原理,首先生成初始种群,对于第i个个体,其行为更新如下[14]:

表1 水利工程质量评价体系
fi=fmin+(fmax-fmin)β
(1)
式中,β—常数,取值范围为[0,1]。
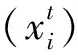
(2)
(3)
式中,x*—所求个体的最优适应度值。
重复上述步骤,当模型达到最大迭代次数时,对所有适应度值进行排序,得到当前最优适应度和关联的位置。
2.3 布谷鸟优化算法
布谷鸟优化算法(CSA)从杜鹃算法中提出,基本原理为:每只杜鹃可以繁殖一颗蛋,然后随机放在一个巢里,这表示一个解。布谷鸟接管了腐烂的蛋,并保留了更好的解为下一代。CSA算法可自主消除最坏的解决方案,保留最优方案[15]。
将t时刻第i只布谷鸟的新解定义为:
(4)
式中,∞—模型步长;⊕—矩阵乘法。
2.4 鲸鱼优化算法
鲸鱼优化算法(WOA)基于鲸鱼觅食的原理实现模型优化[16]。鲸鱼在运行迭代t(Xt)时,在最佳解(X*)的目标猎物周围的潜在位置表示为:
(5)
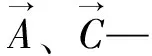
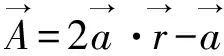
(6)
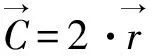
(7)
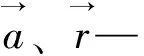
2.5 TOPSIS模型
基于TOPSIS模型对水利工程质量评价体系进行综合评价[17],首先计算不同指标正、负理想解距离计算,具体公式如下:
(8)
(9)
式中,Si+、Si-—各指标与正、负理想解的距离;xi+、xi-—各指标集的正、负理想解。
通过计算相对贴近度εi,作为水利工程质量评估的依据,具体公式如下:
(10)
3 结果与分析
3.1 模型算法选择
由于不同机器学习模型计算的精度不同,本文基于3种优化算法优化ANN模型,计算了不同年份模型对评价指标的模拟精度箱线图,同时将算法结果与梯度提升树(XGB)、随机森林(RF)、广义回归神经网络(GRNN)、小波神经网络(WNN)、极限学习机(ELM)、BP神经网络共6种传统机器学习模型进行对比,结果如图1所示。图1中反映了不同模型决定系数R2和模型效率系数Ens的数值,由图中可以看出,经优化后的ANN模型精度高于其余模型,同时,CSA-ANN模型精度最高。
3.2 模型参数选择
CSA-ANN模型在不同年份模型精度最高的最优隐含层个数如图2所示。由图2中可以看出,当模型所选取的隐含层节点个数不同时,模型精度存在明显差异。当模型隐含层节点个数分别取23、26、4、5时,模型在4个年份的精度最高。
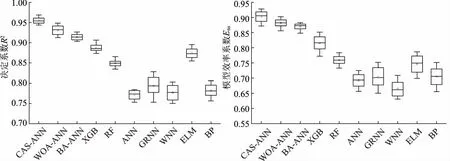
图1 不同算法效果比较箱线图
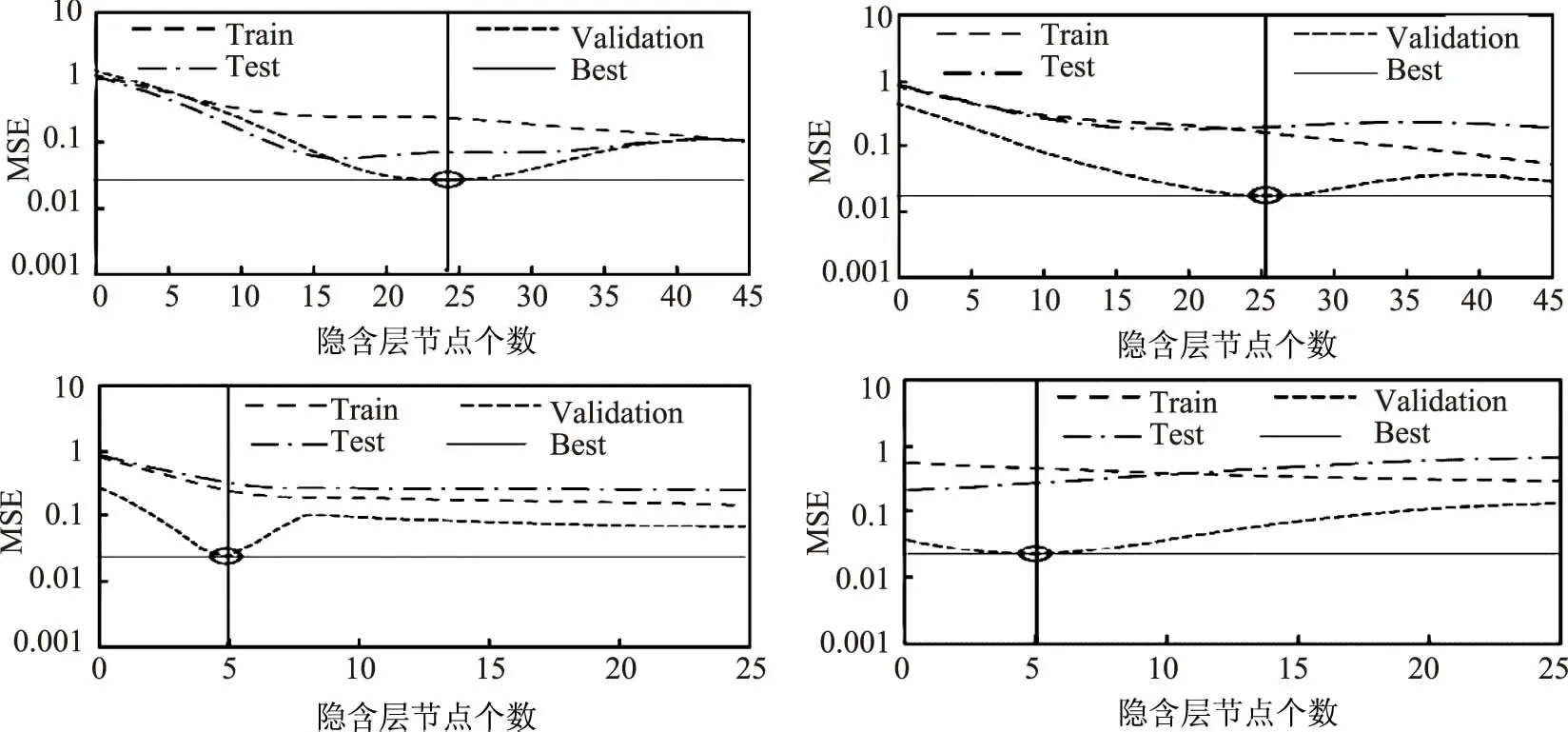
图2 不同年份CSA-ANN模型最优隐含层个数选择
3.3 水利工程质量综合评价
根据水利工程质量评价体系,结合2017—2020年的实际统计数据,总结了4年指标数据的相对隶属度矩阵,结果见表2。基于CSA-ANN模型,可得出不同年份下层评价结果,结果如图3所示。由图3中可以看出,从3个准侧层方面来看,项目操作质量、项目管理质量和项目监理监督质量均表现为2020年分值最高,2019年分值次之,表明随着年份的增加,水利工程质量基本呈上升趋势。
结合下层指标自适应评价结果,基于TOPSIS模型,得出水利工程质量在不同年份的综合评价结果,结果见表3。表3中比较了本文方法与传统层次分析法、模糊综合评价法的结果,由表中可以看出,本文方法评价结果与传统的层次分析法和模糊综合评价法基本一致,均表现为2020年水利工程质量最高。但不同方法的建模时间不同,本文方法的运算时间仅需15.12s左右,而层次分析法和模糊评价法的运算时间分别为1000s和1200s左右,表明本文方法可在保证精度的同时,提高运算效率。
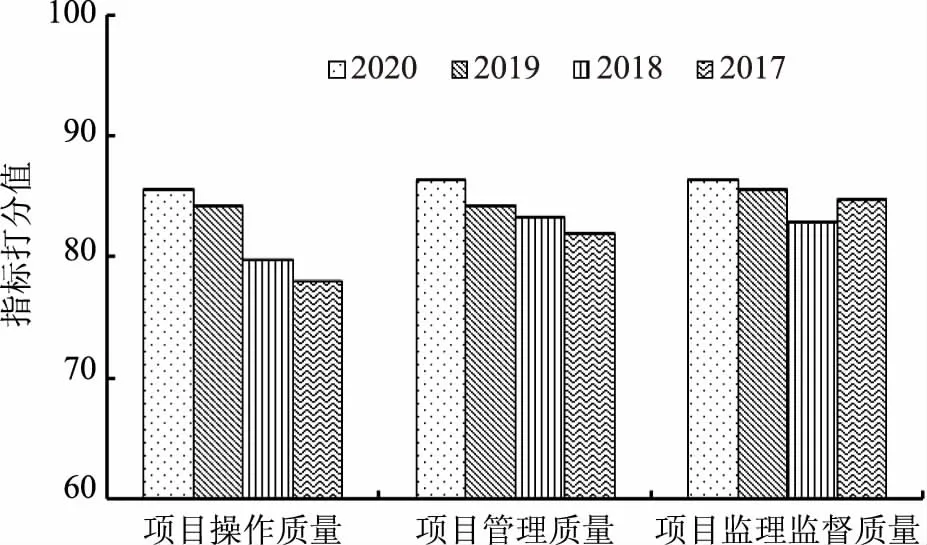
图3 不同年份下层指标自适应评价
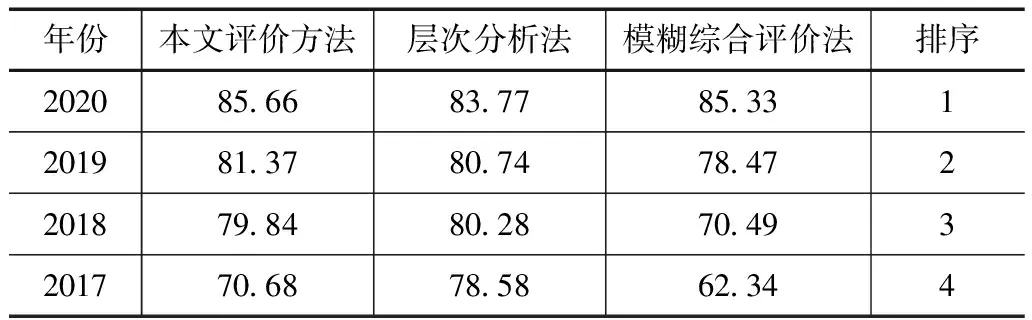
表3 不同方法综合得分对比
4 结论
本文构建了水利工程质量综合评价体系,同时基于CSA-ANN模型和TOPSIS模型对水利工程质量进行了综合评价,指出在比较不同模型精度时,CSA-ANN模型精度最高,其决定系数R2和Ens均在0.90以上,精度明显高于BA-ANN、WOA-ANN及其余传统机器学习模型。本文基于CSA-ANN模型对下层指标进行自适应评价,基于TOPSIS模型对整个评价体系进行综合评价,确定了在2017—2020年不同年份模型的最优隐含层节点个数,同时将评价结果与传统层次分析法和模糊综合评价法进行了比较,证明了该方法的科学性。
本文基于布谷鸟优化人工神经网络模型构建了水利工程质量综合评价模型,在今后的研究中可将该模型应用于建筑工程、水利工程投资风险评价等多项研究中,进一步讨论该方法的科学性。
