基于人工神经网络的电网负荷数据分类方法
2022-04-08花洁,李伟
花 洁,李 伟
(广东电网有限责任公司 佛山供电局,广东 佛山 528000)
在进入能源时代后,社会对于电力的需求都在逐年上升,与此同时产生了大量的电网负荷数据。电网负荷数据中包含着电力系统对用户的电力供应、电价计算、电力负荷预测等,具备极为广阔的现实意义。在电力系统中若电网负荷数据出现错误,会导致一段时间内该地区的电力供应都会失去调配能力。为能够更高效率地利用电网负荷数据,对其进行数据分类处理[1]。
文献[2]通过收集大量的电网负荷数据,基于K-均值算法对电力数据进行了分析与预测。通过大数据的关联分析,递增电网数据的维度,提供了一个电力数据的分类模型。这种方法需要首先建立电网数据的数学模型,依赖于大数据的云计算能力,在计算时耗时较长,效率较差。文献[3]通过神经网络算法针对数据集进行了改进,以采样技术为中心,改变了数据集的识别能力,并创建原始数据集和测试数据集作为电网负荷数据的分类样本。这种方法通常只适用于比例适中的小样本数据集,对于大数据样本的计算能力较差。文献[4]通过聚类算法,设计了一种能够向上采样的数据集,在调整计算样本的过程中,设定合适的参数结构,进而提高后续算法的计算准确性,保证冗余数据被及时删查,但是这种算法需要改变数据的分布结构,才能增强数据分类效果,因此在某种情况下无法使用。
为解决以上传统方法存在的问题,本文通过人工神经网络算法,对电网负荷数据的分类算法进行改进优化设计。从另一个角度,删减数据库中的冗余数据,减少数据的数量,进而增强电网负荷数据的分类效率。
1 电网负荷数据分类方法
1.1 提取离群点数据
假设在数据集中,需要保证分类器的整体性能近似于平衡状态,此时数据密度计算公式为:
(1)
式中,ρd为数据集M中,当分类器处于平衡状态时样本数据的密度;Nd为样本数据大类中的样本数量;Nx为样本数据小类中的样本数量;Nl为样本数据的邻近样本数量。
当ρd的函数区间位于[0,1]时,其最大容忍度可以表示为:
(2)
式中,ξmax为欧式几何模型中数据样本的最大容忍度;ρNd为数据模型中大类样本的密度;ρi为数据模型中样本的总密度[5-6]。一般的邻近样本需要在数据集Ui中得到采样的最近邻密度,因此可以通过计算局部密度的方式得到其距离中心点的可达性。
(3)
式中,ρlrd(Hn)为数据集Hn局部的面积最大值;Im为距离数据集Hn最近的对象与数据集Hn中心的距离;d(xn-xi)为数据集一段端点xn与另一端端点xm的距离;Nh(Pl)为离群点数据与数据集中心的可达性[7-8]。通过计算ρlrd(Hn)的最大值,可以得到离群点数据的采样依据,若ρlrd(Hn)大于1,则表明可以检测到离群点的采样数据,若ρlrd(Hn)小于1,则表明无法检测到离群点的采样数据。
1.2 训练集设计
在人工神经网络算法中,对数据集的训练大致可以分为4个步骤,首先需要通过计算可达性得到离群点数据的采样结果,并保留下采样中的边界样本。在构造原始数据集时,需要将子集中的样本整理到母集中,以保证数据集的噪声数据可以被移除。第2步需要将数据集中所有的噪声数据全部清除,以下为检验噪声数据的公式:
(4)
式中,Tr(θ)为数据集θz中需要被清理的噪声数据的位置;Nz为在找到噪声数据前最后一个被训练的数据;λn为对样本λ第一个计算初始目标的神经元输出值;λm(θ)为对样本第一个计算初始目标的神经元目标值[9-11]。在得到噪声数据的检验方法后,需要将上文中的数据分区块小规模训练,通过权值迭代的方法将隐藏节点作为分区标志,计算隐藏节点与输出节点之间的向量坐标:
(5)
式中,λj(θ)为在以隐藏节点为边界的小规模数据库中,隐藏节点与输出节点之间的向量坐标;Hn(θ)为隐藏节点的数据变化梯度;Gm(θ)为输出节点的数据变化梯度。为了提高学习效率,可以将隐藏节点与输出节点设定为双向激励函数:
(6)
式中,αm为通过人工神经网络学习的效率值[12]。通过这个双向激励函数,在大范围的数据库中建立训练集,并获得相应的训练阈值,以达到人工神经网络算法中数据集的训练目的。
1.3 电网负荷数据逼近优化
利用以上神经网络算法,可以分别计算隐藏节点与输出节点之间的激励函数,并确定冗余数据的确切位置,在此之后,需要进一步优化人工神经网络中的数据分类功能,使其成为特征区间中的最优值。数据分类流程如图1所示。
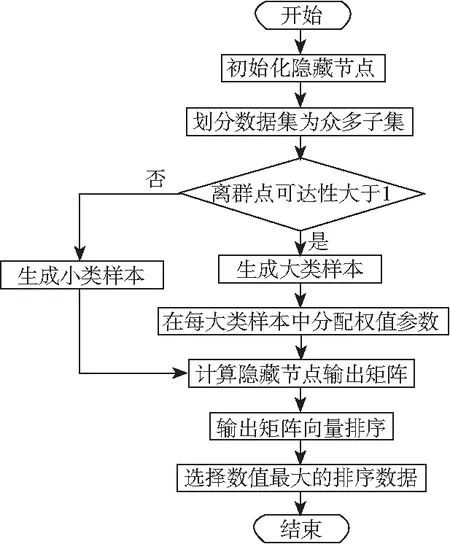
图1 数据分类优化Fig.1 Data classification optimization
如图1所示,通过离群点的可达性判定,可以将数据母集分为不同的子集,其中数量较大的部分为大类样本,数量较小的部分为小类样本[13-14]。在计算了隐藏节点的输出矩阵后,可以通过计算矩阵向量排序的方式获取其最大数值,再计算每个样本的累计误差,该误差的最小化计算方法为:
(7)
式中,μmax为数据样本中累计误差的最小化参数;αm为调节参数的累加平均值;αn为调节参数的极值识别系数。计算出μmax最大的数据,就可以得到特征区间中的最优值。
1.4 生成冗余数据周期性筛查模型
在训练了数据集之后,还需要将数据集中作为边界的冗余数据全部清除。通常情况下,需要设定原始的数据样本n1,n2,n3,…,nx,在每一个小范围的样本数据集中,都能够得到冗余数据的周期平均值:
(8)
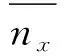
该周期平均值的周期指数可以表示为:
(9)
式中,Ti为该周期平均值的周期指数。
通过以上周期平均值和周期指数的计算,可以直接通过网络结构计算出冗余数据的误差更新阈值:
(10)
式中,Fwc为网络结构中冗余数据的误差更新阈值;nx为数据集中最后一个冗余数据的位置坐标;ni为数据集中第i个冗余数据的位置坐标。
在电网负荷数据中,这个冗余数据的阈值就可以通过二分法进一步确定缩小其区间范围,计算公式为:
(11)
式中,θr为该数据集中电网负荷冗余数据的位置坐标;tr-1为该电网负荷冗余数据筛查模型的前2个区间范围中位置坐标;tr-1为该电网负荷冗余数据筛查模型的前一个区间范围中位置坐标[16]。
通过式(11)可以逐步确定冗余数据的位置,并将其清除,该公式就是电网负荷冗余数据周期性筛查模型。
2 实验设计与研究
2.1 实验准备
本文实验主要目的为检验上文中基于人工神经网络算法的电网负荷数据分类方法的性能,在此过程中,将其与常规的3种算法进行对比,以此判断文中的数据分类方法是否实现了性能的优化。收集电网中的运行数据,分3次在其中随机抽取100组数据,分别为数据集A、数据集B、数据集C,这3个数据集的属性设置见表1。
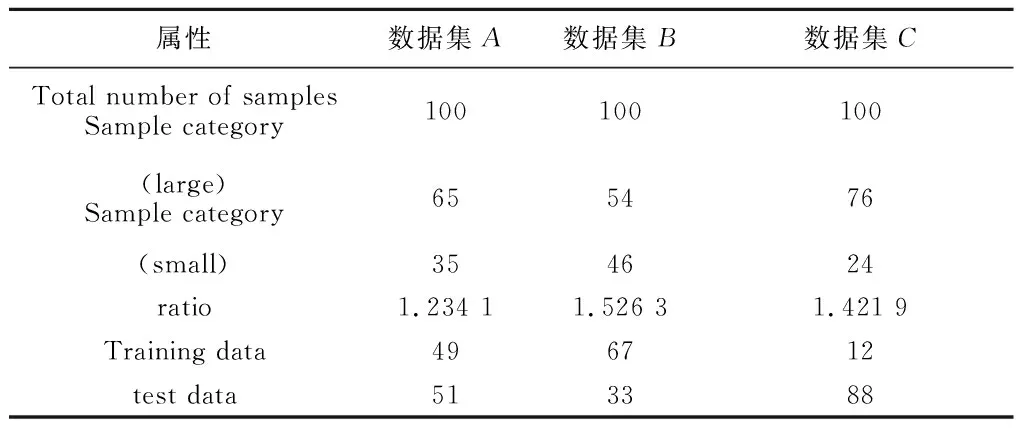
表1 数据集属性设置Tab.1 Dataset property settings
在若干电网负荷数据中,分类的操作十分复杂,其中包含着许多没有作用的冗余数据,在分类之前因此需要将这些冗余数据首先筛除,此时就需要通过信噪比来判断4种算法中电网负荷数据分类方法的性能,其计算公式为:
(12)
式中,gx(t)为某算法中电网负荷数据分类信噪比的计算结果,一般情况下gx(t)越大,说明该段数据中的冗余数据含量越小,反之则越大;ηx1为在数据库中数据集A所含有的水平均值;ηx2为在数据库中数据集B所含有的水平均值;ηx3为在数据库中数据集C所含有的水平均值;δy1为在数据库中数据集A所含有的水平标准差;δy2为在数据库中数据集B所含有的水平标准差;δy3为在数据库中数据集C所含有的水平标准差。
2.2 电网负荷数据信噪比测试
在3个数据集中构建10个隐藏节点,每经过一个隐藏节点计算一次电网负荷数据的信噪比。将文中设计的数据分类方法作为实验组,将文献[2]方法、文献[3]方法以及文献[4]方法作为对照组1、对照组2和对照组3,分别将以上数据代入到数据分类方法中进行测试,得到如图2所示的实验结果。
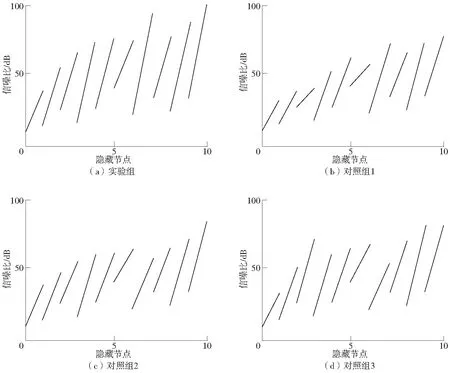
图2 电网负荷数据信噪比测试Fig.2 Power grid load data signal-to-noise ratio test
电网负荷数据在10个隐藏节点中的信噪比如图2所示,整理图中的数据,得到表2—表4。
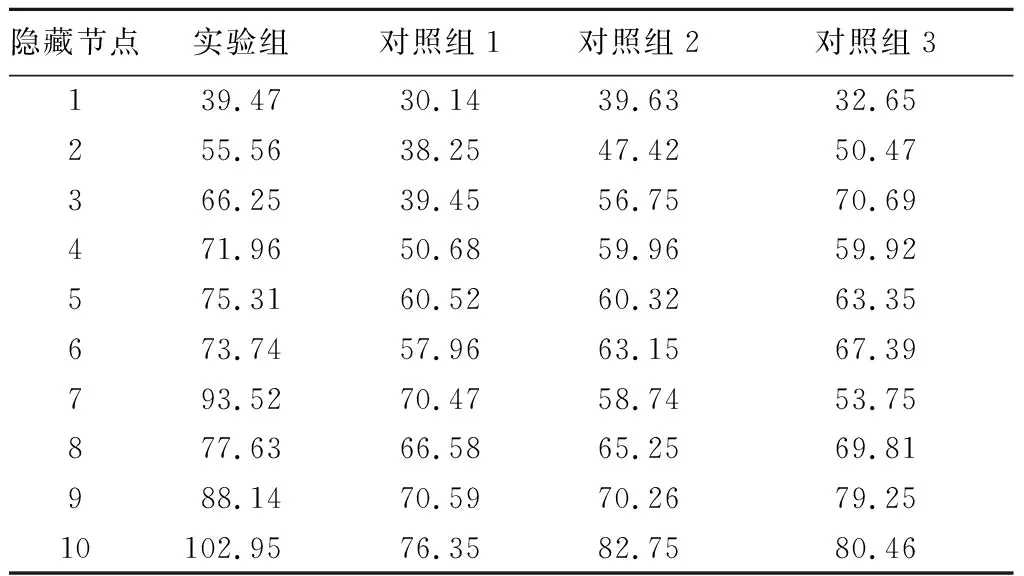
表2 数据集ATab.2 Dataset A
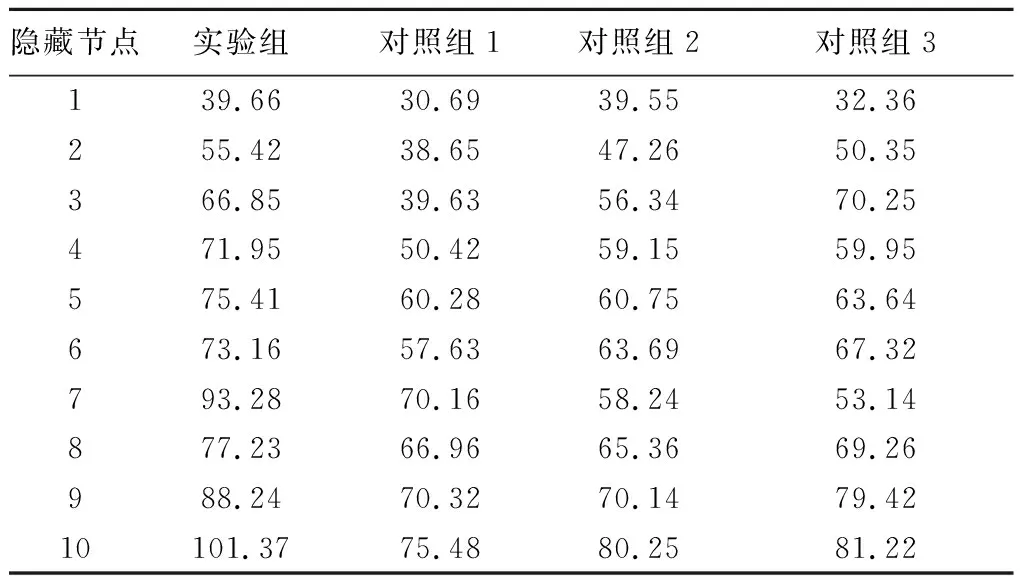
表3 数据集BTab.3 Dataset B

表4 数据集CTab.4 Dataset C
对照组1在3个数据集中的信噪比分别为76.35、75.48、75.96 dB,对照组2在3个数据集中的信噪比分别为82.75、80.25、79.24 dB,对照组3在3个数据集中的信噪比分别为80.46、81.22、80.99 dB。综上所述,文中设计的基于人工神经网络的电网负荷数据分类方法较常规的3种方法信噪比更高,对冗余数据的清除更彻底,可以得到更准确的分类方法。
在以上3个数据集中,4组算法得到的最大信噪比即是其最终信噪比。其中,实验组在数据集A中的信噪比为102.95 dB,在数据集B中的信噪比为101.37 dB,在数据集C中的信噪比为100.96 dB。
2.3 不同方法分类性能对比
将文中设计的数据分类方法作为实验组,文献[2]方法、文献[3]方法以及文献[4]方法作为对照组1、对照组2和对照组3,测试不同方法的负荷数据分类综合性能(分类准确率、精度、召回率),得到如图3所示的实验结果。
根据图3的实验结果可知,与对照组的3种方法相比,研究方法具有更高的分类准确率、精度以及召回率。在30次的实验迭代过程中,研究方法的准确率可稳定在90%以上,精度和召回率可达80%以上。以上实验结果表明研究方法具有理想性能,应用性更强。
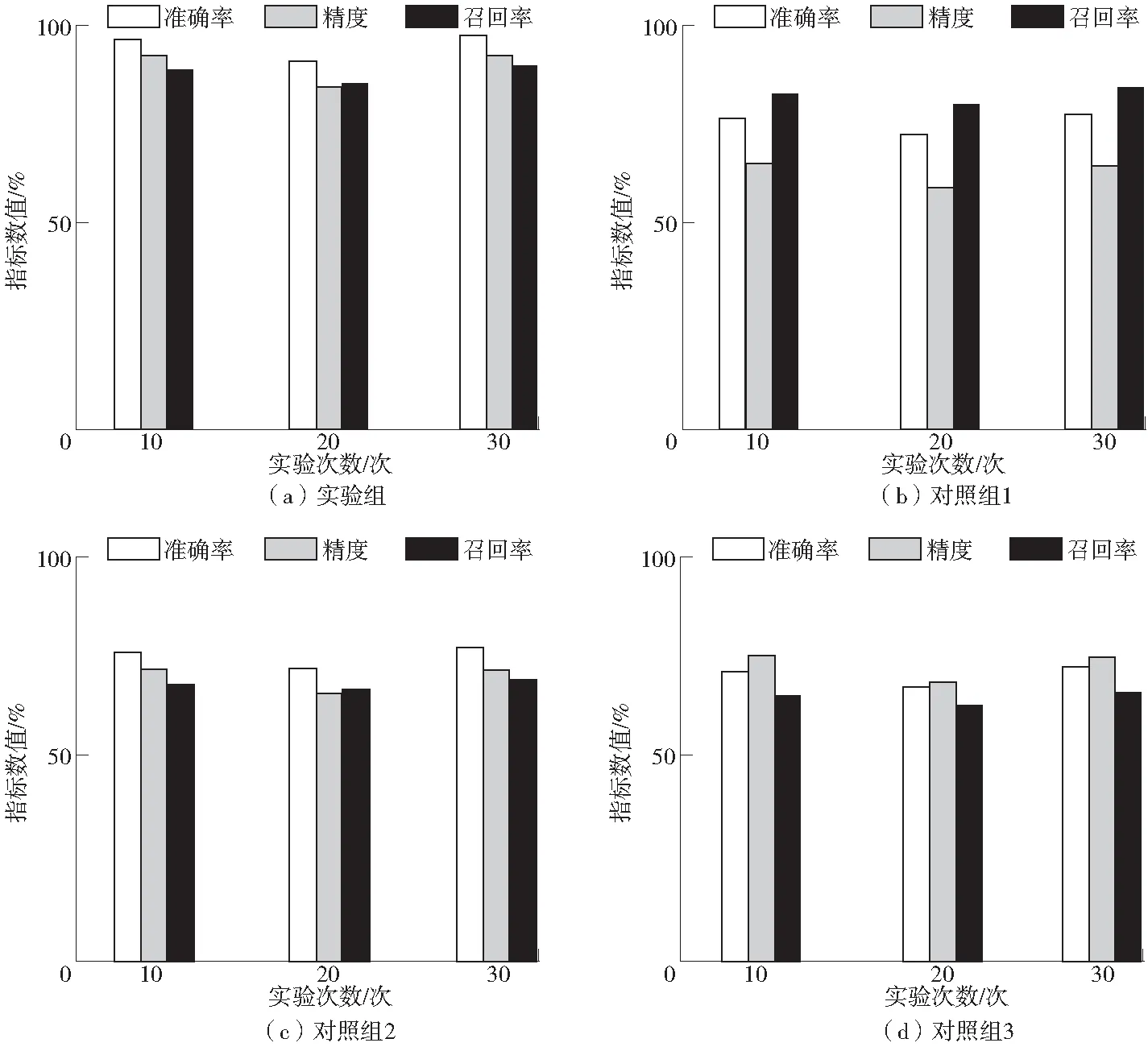
图3 3种方法的分类性能对比Fig.3 Comparison of classification performance of three methods
3 结语
通过人工神经网络算法设计了一种电网负荷数据分类方法,该方法以清除冗余数据为核心,保证了数据库中数据节点的完整性和简洁性,提高了电网负荷数据的信噪比,从另一个角度提高了数据分类的运算速度,保证了数据分类的准确性。
